基于数值模拟的输电铁塔主角钢加固研究

何荣卜，马晓红，毛先胤，王勇，余启春，华建坤

(1.贵州电网有限责任公司电力科学研究院，贵州 贵阳, 550000；2.中国电建集团贵州电力设计研究院有限公司，贵州 贵阳，550000；)

随着重覆冰架空输电线路设计技术规范的发布[1]，一部分早期建造的输电塔在极端荷载下承载力已不满足新规范的要求[2]。针对不同控制工况，找出铁塔薄弱部位[3-10]，并进行加固补强是一种经济实用的方法[11-14]。Qiang X等[15]在分析铁塔破坏机理基础上，提出一种加固输电塔斜材的方法，对加固前后的塔架组件进行了实验研究和有限元模拟。李文斌等[16]提出了一种在既有输电塔构件上进行Y字形加固的无须焊接技术方案。沈之容等[17]考虑初始负载的影响，进行了方形和L形两种截面焊接加固角钢的实验与数值模拟。苏子威[18]对夹具连接十字型组合截面加固输电塔单角钢构件进行了实验和有限元分析。众多学者研究的加固方案[19-24]对角钢稳定承载力均有明显提高，然而这些方案对于提高角钢强度承载力却几乎没有效果。实际上受螺栓减孔影响部分塔身主材的承载力是由强度控制的，提高这些主角钢稳定承载力，并不能起到加固输电铁塔的目的。基于此，本文提出了一种采用螺栓连接，在主材上并联不等边角钢的加固方法，来提高角钢的强度承载力。

1 有限元模型

1.1 模型主角钢的几何参数与受力性能分析

本文有限元模型中主角钢的几何参数，取自贵州电网500kV单回路输电线路中的典型耐张塔JG22。主角钢长度4074mm，型号为Q355L160X14，该主材所在塔身段正侧面如图1所示。横担处(图1中主材上端)主角钢正面采用双排M20螺栓通过节点板与导线横担相连，侧面采用单排M20螺栓利用节点板与横隔相连；瓶口处(图1中主材下端)两侧均采用单排M24螺栓利用内包角钢外贴板与下部主材相连。

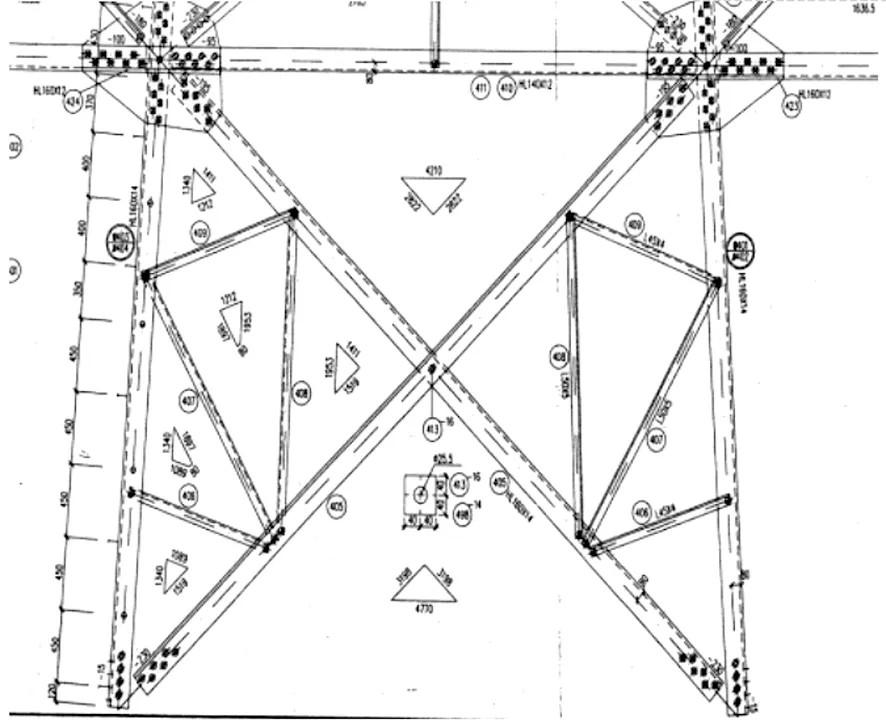
图1 (a)模型主材塔身段正面Fig.1 (a)Front side of the main timber tower section of the model

由《架空输电线路杆塔结构设计技术规定》(DL/T5154—2012)角钢轴心强度承载力可以按式(1)计算，轴心受压稳定承载力可按式(2)计算。

N=m·f·An

(1)

N=mN·f·ψ·A

(2)

上式中：

N—轴心拉力或压力设计值；

m—构件强度折减系数，双肢连接的角钢m值取1；

mN—压杆稳定强度折减系数，对本例mN值取1；

ψ—轴心受压构件稳定系数，对本例ψ值取0.842；

A—构件毛截面面积；

An—构件净截面面积；对多排螺栓连接的构件，要计及锯齿形破坏情况；

f—钢材的强度设计值(为与有限元材料属性保持一致，这里取钢材的屈服强度)。

由《架空输电线路杆塔结构设计技术规定》(DL/T5154—2012) 可得受拉角钢减孔数n=2.35。

查《钢结构设计手册》可知L160×14角钢的截面面积为43.30cm2。

因此An=4330-(2.35×21.5)×14=3622.65mm2代入式(1)可得轴心强度承载力N=1286.04kN。由式(2)可得轴心受压稳定承载力N=1294.28kN。对比式(1)与式(2)的结果可以看出，该角钢的承载力是由强度决定的。

JG22设计条件为20mm冰，基本风速(10m高)30m/s；导线型号LGJ-400/50，地线型号LBGJ-100-20AC。根据《重覆冰架空输电线路设计技术规程》(DL/T5440-2020)计算可得该主材轴心压力外荷载为1308.3kN(按屈服强度计算)，大于构件的承载力，因此需对该构件进行加固，以确保输电铁塔在设计条件内安全运行。

1.2 模型的建立

本次数值模拟共建立三个几何模型，分别命名为模型1、模型2、模型3。模型1为加固前主角钢模型，模型2为主角钢双侧并联不等边角钢加固模型，模型3为主角钢单侧并联不等边角钢加固模型。为了方便有限元网格的划分建立模型时仅保留了角钢肢背内部圆角，以直角代替肢尖倒角。螺栓孔径按照实际取值，螺栓直径与螺栓孔径尺寸相同，以圆形螺母和螺帽代替六角头型。为简化模型取消了辅助材，在原角钢辅助材支承处设置厚度14mm、宽度为60mm的垫片，对垫片施加与辅助材支承方向相同的弹簧约束，来模拟辅助材对主材的支承作用。内贴角钢与外贴板厚度均与主角钢相同，不等边角钢两肢宽分别160mm和100mm，厚度10mm。利用主角钢上现有螺栓孔将不等边角钢并联在其外侧，同时参考《钢结构设计标准》(GB50017-2017)，对双角钢受压组合构件两个侧向支承点之间的填板数不应少于2的规定，这里除利用原角钢的螺栓孔连接加固件外，还在原角钢每个侧向支承间各增加两个连接螺栓，各模型如图2所示。

图2 (a)模型1Fig.2 (a) Model 1

1.3 模型本构关系与边界条件

主角钢和并联的不等边角钢本构关系采用双线性等向强化模型，钢材达到屈服应力后切线模量Et取为0.02E，屈服强度取355MPa。本文中螺栓和节点板不是主要研究对象，认为螺栓和节点板强度足够，因此将螺栓与节点板看作理想的线弹性材料，弹性模量与角钢相同，各本构关系如图3所示。根据《钢结构设计标准》(GB50017-2017)钢材弹性模量E=206GPa。

图3 (a)双线性等向强化模型Fig.3 (a) Bilinear isotropic strengthening model

工程计算中将铁塔主角钢两端约束看作铰接，模型与工程计算保持一致，对主角钢瓶口端外贴板和内贴角钢施加铰接约束。由图1可以看出主材在横担处并未断开，所以将横担处主角钢截面作为施荷面，把该截面X、Y、Z三个方向的自由度与一参考点耦合，仅放开参考点Z方向自由度(Z方向为沿主材轴线方向)对参考点的Z方向施加荷载或者位移。假设螺栓和螺母连接可靠，采用绑定约束简化螺栓与螺母的相互作用。模型中各接触面间的法向接触属性采用硬接触，切线方向的摩擦系数取0.15。

1.4 模型单元与网格

采用非线性分析有限元模型，模型中角钢尺寸较大且螺栓连接构件间存在大量接触，为避免出现体积闭锁现象，降低计算时间故不采用完全积分单元、二次积分单元与修正的四面体单元。线性减缩积分单元只在单元的中心有一个积分点，可以避免剪切闭锁问题，而且单元形状对其计算精度影响不大，它在积分点上的应力结果是相对精确的，但经过外插值和平均后得到的节点应力则不精确。由于螺栓孔处存在应力集中，为得到较精确的节点孔壁压力故也不予选择。非协调单元的计算精度很接近二次单元的结果，而计算代价远远低于二次单元，因此选用非协调单元。

网格的划分对计算结果有很大影响，为保证应力集中处的精度，螺孔处网格更加细化，同时为提高计算效率，其他部位网格相对较粗，模型1网格如图4所示。有限元网格并不是越密越好，也没有普遍适用的网格密度，为了选择合适的网格密度采用扫掠的划分方式，对模型1角钢厚度方向划分两个网格，长度方向网格尺寸取0.02m，网格长宽比为4∶3，其他位置保持不变，螺孔处分别划分20和32个网格种子，来验证不同网格密度对计算结果的影响。

图4 模型1网格图Fig.4 Mesh diagram of model 1

模型分两步施加荷载，第一步：在螺栓上施加500N的预紧力，模拟螺栓对各构件的紧固作用。第二步：保持螺栓预紧力不变，对参考点Z方向施加0.01m的位移荷载，模拟外荷载对主角钢的作用。根据螺孔处网格种子的个数，将不同网格下的计算结果对应命名为模型1-20和模型1-32，模拟获得的荷载位移曲线如图5所示。

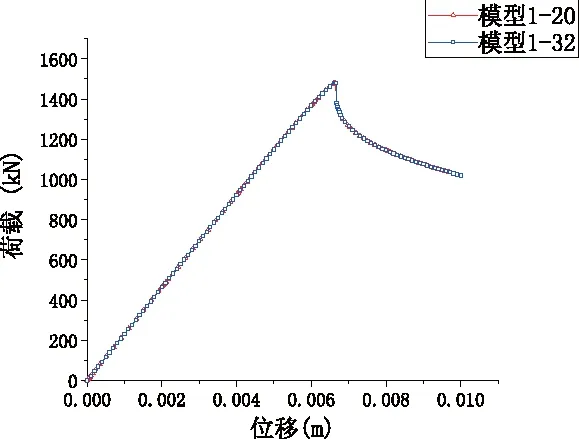
图5 两种网格下模型1的荷载-位移曲线

从图5中的荷载-位移曲线可以看出两种网格下的计算结果差异很小，模型1-20的最大荷载为1481.7kN，模型1-32的最大荷载为1480.5kN，两者仅相差0.081%，由此可见当前的网格密度已经可以保证整体分析精度了。

接触问题属于高度的边界非线性问题，在使用有限元计算触面间的相互作用之前，需要将接触面区分为主面和从面。一般而言选择刚度更大、网格更粗糙的面作为主面，从面的网格尺寸要比主面更精细，不合适的网格尺寸会增加大量计算时间且容易导致计算结果不收敛。经试算对于此次模拟中的加固构件组合，当螺栓孔处网格种子设置为28个时，有利于模型计算结果的收敛，因此对于加固构件组合，螺栓孔处均布置28个种子。虽然加固前后主角钢的网格种子密度不同，但是由上述分析可知，这些不同引起的误差可以忽略不计。

2 有限元模型的计算结果

取前述模型1-32的结果作为加固前主角钢的有限元模拟结果，(为了方便下文均以模型1代指模型1-32)。根据施加位移荷载的位置，将模型2区分为模型2-1和模型2-2。模型2-1的施荷位置与模型1相同，在横担处主角钢截面上；模型3和模型2-2的外荷载均施加在横担处外贴板上。

计算得到的各模型的应力云图如图6、7、8、9所示，其中螺栓预紧力云图仅取模型1的作为代表，全部模型的荷载位移曲线绘制在图10中。

图6 (a)模型1螺栓预紧力应力图Fig.6 (a) Strain diagram of bolt pretightening force inmodel 1

图7 模型2-1位移最大时应力图Fig.7 Strain diagram for maximum displacement of model 2-1

图8 (a)模型2-2荷载最大时应力图Fig.8 (a) Strain diagram of model 2-2 under maximum load

图9 (a)模型3荷载最大时应力图Fig.9 (a) Strain diagram of model 3 under maximum load

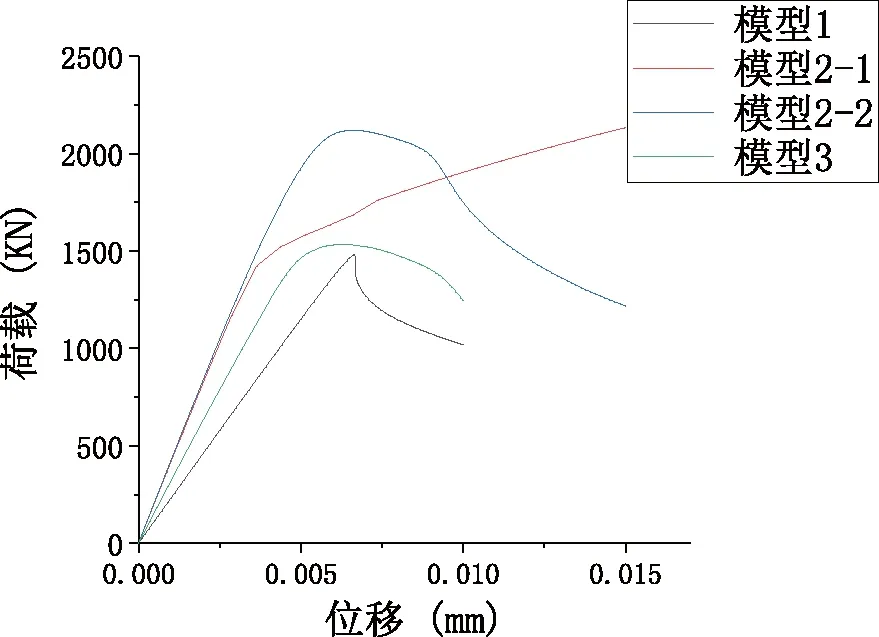
图10 荷载-位移曲线Fig.10 Load-displacement curve of the model

结合图6和图10中模型1的荷载位移曲线可以看出，模型1主角钢螺栓减孔处存在明显的应力集中，在位移荷载作用下螺栓孔处首先发生局部屈服，当荷载达到最大时继续施加位移，螺栓孔处的局部屈服将会引起整个构件的不稳定失稳，主角钢承载力急剧下降，结构遭到破坏。

模型2-1的位移荷载直接施加在横担处主角钢截面上，由图7中模型2-1的应力云图可以看出，当双侧并联不等边角钢加固时，如果荷载施加在主角钢上，主角钢受荷处会首先出现塑性变形，加固后结构整体变形不协调。这表明新增加固构件并不能与原角钢协同受力，这一现象与Barran[25-27]等对并联构件加固角钢的实验和数值模拟结果相似，即此时加固件并未有效改变荷载的传递途经。因此如果加固处荷载是由主材直接承受时，不能只加固承载力不足的主材，必须将对主材的加固向上延伸一个塔身段或者加固到主材开断处，来确保加固件与原角钢协同受力。图10中模型2-1的荷载位移曲线也很好地印证了这一点，开始时主角钢处在弹性阶段荷载位移关系呈线性变化，当荷载继续增加到主角钢发生完全塑性变形时，由于并联不等边角钢对主角钢具有约束作用，主角钢并不会立即丧失承载力，整个结构的荷载-位移行为会按照图(2)中定义的材料本构关系，双线性等向强化模型的塑性阶段发展，但是此时主角钢横担处截面已发生全面屈服，因此增加的承载力不具有工程应用的价值。

模型2-2中的位移荷载施加在横担处的外贴板上，从图7中可以看出改变荷载施加位置后，加固件和原角钢可以协同受力，组合构件先在螺栓减孔处出现局部屈服，当荷载达到临界值时，继续施加位移荷载构件整体发生失稳破坏。图10中模型2-2的荷载位移曲线表明加固后的角钢承载力显著提高，下降段与模型1相比也更加平缓，这说明加固后构件的失稳模式更接近于平衡失稳。

为避免出现模型2-1中的情况，模型3的荷载施加在横担处外贴板上。采用单侧并联不等边角钢的加固方法，显然加固后组合构件的截面不再具有原对称性，若继续施加位移荷载则由于加固后角钢两肢截面面积相差很大，两肢承受的荷载也会因此出现较大差异，这与实际工程不符，因此将位移荷载改为力荷载。图8表明构件的屈服区首先出现在未加固侧的螺栓孔处，当荷载达到最大值后，继续增加荷载加固后的组合构件将会发生失稳破坏丧失承载力。从图10中模型3的荷载位移曲线可以看出，单侧并联不等边角钢，对原角钢承载力提升很小，只对原角钢失稳时承载力减小幅度有较大改善。

3 模拟结果与规范计算结果的对比

由《钢结构加固设计标准》(GB51367-2019)轴心受拉或者轴心受压构件增大截面加固后强度可按式(3)计算：

N=ηn·f·An

(3)

式中：N——计算构件所承受的总轴心力(N)；

An——加固后构件净截面面积(mm2)；

f——钢材强度设计值(MPa)，取截面中最低强度级别钢材的强度设计值(为与有限元材料属性保持一致，这里取钢材的屈服强度)；

ηn——轴心受力构件加固强度修正系数，对模型2取0.75，对模型3取0.675。

考虑螺栓减孔影响，模型2的净截面面积为7824.95mm2，模型3的净截面面积为5507.95mm2。将模拟得到的最大承载力与按式(3)计算得到的理论承载力列入表1中，并且将他们相对各自理论值的百分比记录在表格的最后一列(不包括模型2-1)。

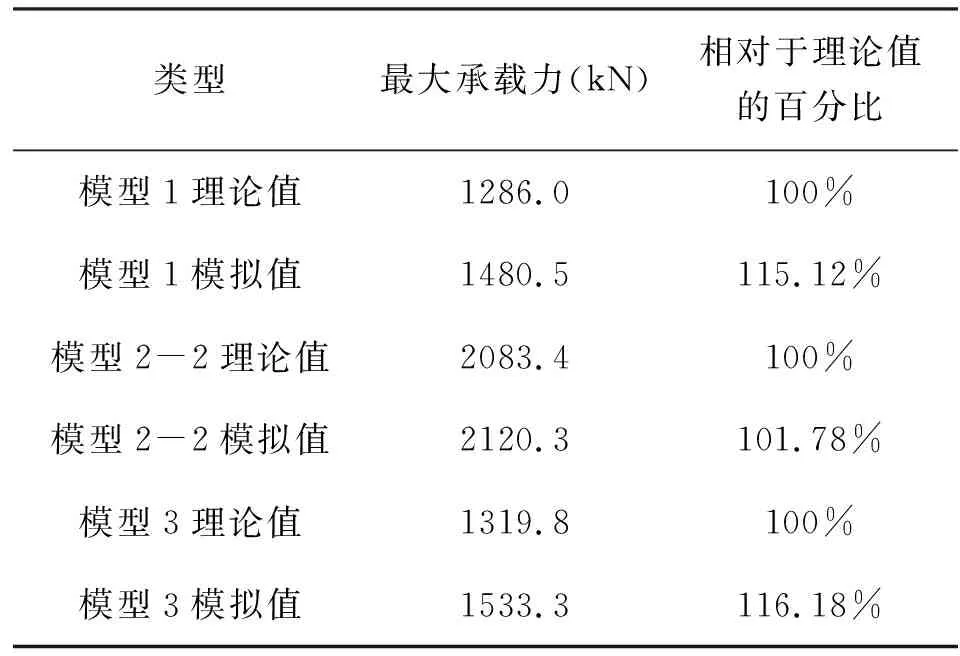
表1 最大承载力的理论计算值与模拟值Tab.1 Theoretical and simulated values of maximum bearing capacity

表1中模型1比其理论值大15.12%，这主要是因为数值模拟时使用双线性等向强化模型，考虑了材料屈服后强度造成的；另外在模拟角钢肢尖处的倒角时，以直角作简化处理，这使得模拟角钢的净截面面积较实际稍大，模型3比其理论值大16.18%与模型1情况接近，这印证了上述原因所引起的误差，在模拟结果中普遍存在。

然而即使受同样的误差因素影响，模型2的模拟值仅比其理论值大1.78%，这表明对于本文中双侧并联不等边角钢的加固方法按《钢结构加固设计标准 》(GB51367-2019)进行理论计算时，加固后构件的安全裕度较单侧加固小。考虑到工程应用时使用钢材设计值代替屈服强度，对于双侧加固仍然可以按照《钢结构加固设计标准》(GB51367-2019)进行设计，但是应适当提高加固构件的设计承载力(根据上述结果建议提高15%)，保证一定的安全储备。

模拟结果中模型2-2和模型3的最大承载力，相对模型1分别提高了43.2%，和3.57%。理论计算结果中模型2-2和模型3的最大承载力，相对模型1分别提高了62%和2.62%。数值模拟和理论计算都表明，对在主角钢单侧使用螺栓连接并联不等边角钢加固，对强度承载力的提高效果很差，不建议工程实践中采取这种加固方式。反之双侧并联不等边角钢加固方法，对原角钢强度承载力有很大提高，可以应用于工程实践中予以采用，但是使用时应注意避免出现加固件与原主材不能协同受力的情况。

4 结论

(1) 采用本文数值模拟参数，对角钢加固方案进行有限元分析获得的结果是稳定可靠的。

(2)在主角钢单侧使用螺栓连接并联不等边角钢的加固方法，对提高强度承载力的几乎无效，仅对其失稳后承载力降低幅度有一定改善，不建议在工程实践中使用。

(3)在主角钢双侧使用螺栓连接并联不等边角钢的加固方法，对强度承载力有很大提高，但使用时应注意如果加固处荷载是直接施加在主材上的，不能只加固承载力不足的主材，必须向上延伸一个塔身段对主材进行加固或者加固到主材开断处，来确保加固件与原角钢协同受力。

(4)可以使用《钢结构加固设计标准》(GB51367-2019)中的公式，对本文提出的单侧并联加固方法进行计算，但是对于双侧并联加固，使用时建议提高15%的设计承载力。