基于连续模型的散料转运料斗曲线设计*

张文超

湖南机电职业技术学院 长沙 410100

0 引言

在冶金、矿业等领域中，散状物料的输送与转载是广泛存在的基本环节，其中转载点料斗更是整个系统的重点，转运料斗设计的好坏严重影响着整个系统的输送效率和运行安全。传统转运料斗采用直线型结构，其具有制作简单、方便安装以及造价低等优点，但随着散状物料处理量及物料的种类不断增大，其不能很好地控制物料流动，导致料斗堵料、扬尘、受料输送带偏载等运行问题日益突出。因此，转运料斗的曲线形设计应用越来越广泛，其设计思路使散状物料实现运动轨迹可控化，防止溜槽堵塞、减小冲击、抑制诱导风、降低粉尘的产生。国内外学者从对散状物料性能进行测试到参数标定离散元模型及实验对比模型，基于离散元（DEM）进行曲线转运料斗的设计方法被广泛研究和应用[1，2]。另外，chen X L等[3]采用流体动力学（CFD）研究了散料卸料下不同形状料斗产生粉尘的规律特征。本文主要基于连续模型理论，将散状物料看成连续整体模型，进行转运料斗的曲线设计。

1 连续模型理论

物料流动的连续模型理论主要基于以下假设[4，5]：1）物料在流动的过程中是连续的；2）影响物料流动的因素只考虑物料与料斗壁的摩擦力，忽略物料内部因素的相互影响；3）忽略空气的阻力。

如图1所示，曲线转运料斗连续模型由直线冲击模型、凸弧段模型、凹弧段模型和抛料模型构成。物料由上带式输送机抛料运动，物料冲击挡料板直线段运动，沿弧形板切向运动，自由落体运动，沿给料匙切向运动，连续输送至下带式输送机。典型曲线转运料斗主要由挡料板、给料匙构成，随着转运高度的增加，增加多段曲线转运溜槽完成料斗的设计。弧形挡料板、曲线转运溜槽、给料匙均是由多段直线段、凸弧段和凹弧段构成，且相邻2段均相切，故上一段的出口速度即相邻下一段的入口速度。

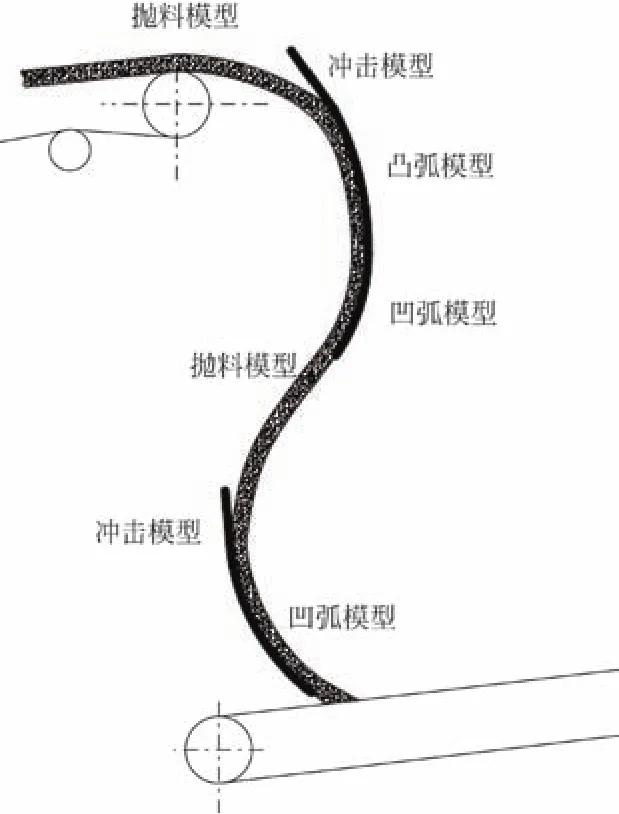
图1 曲线料斗连续模型

因物料流动过程是连续的，流动性方程为

式中：ρ为散料密度，A为散料流动横截面积。

2 结果与讨论

2.1 直线冲击模型

在曲线转运料斗设计中，模型主要是避免物料撒料，使物料更好的进入料斗中。直线冲击模型末端与凸弧段或凹弧段相切的迎料点是改变物料速度的关键。如挡料板中直线段与凸弧段相切，给料匙直线段的迎料点与凹弧段相切的迎料点，故直线冲击模型末端迎料点的计算决定着物料进入料斗内的初始速度。

2.1.1 模型计算

取连续体模型中单位物料△m，物料进入冲击模型迎料点时，保证物料沿料斗壁运动，理论计算基于动量定理，即物体所受合外力的冲量等于其动量的增量。冲量表述了对物料作用一段时间的积累效应的物理量，是改变物料运动状态的原因。图2所示迎料点冲击模型，模型计算为

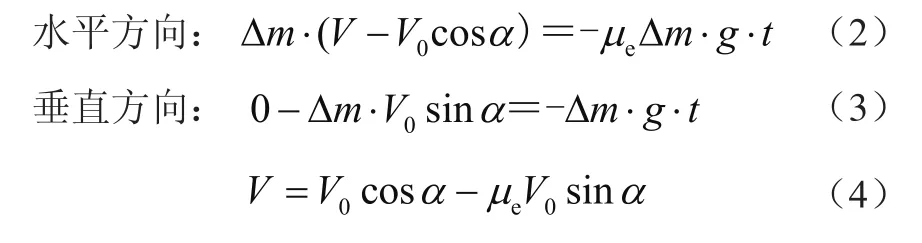
图2 迎料点冲击模型

2.1.2 变量分析

在冲击模型迎料点处，物料的速度V受初始速度V0和等效摩擦系数μe及切入角α的因素影响，根据式（4）建立如图3所示相应的变量分析。

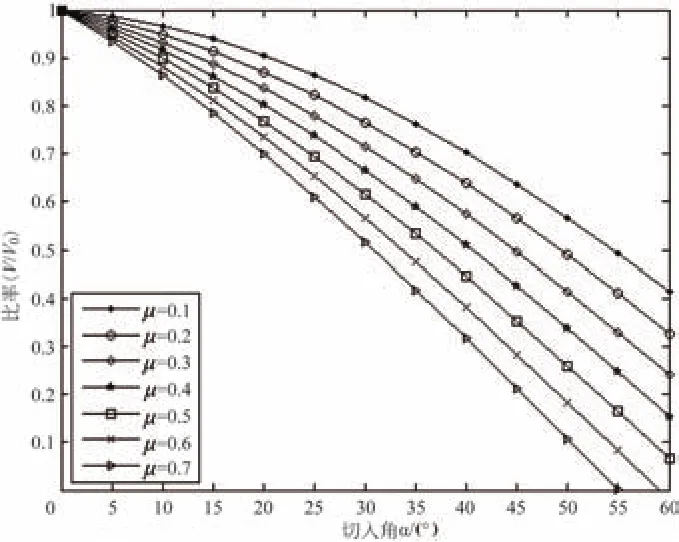
图3 不同摩擦系数下切入角与速度比率关系曲线图

在图3中，速度比率系数均小于1，计算速度V整体小于初始速度V0，表明物料冲击切入料斗直线段时，产生不可避免能量损失。相比等效摩擦系数μe，切入角α的变化对系数产生显著的影响。在料斗的快速设计中，等效摩擦系数μe为常量，由物料的料性、物料与料斗壁的摩擦来决定。切入角的设计才是冲击模型设计的关键，由图3可知，切入角α宜选在10°～ 30°，角度过小不能很好地包裹物料，易发生撒料的情况；角度过大能量损失过多，显著降低了计算速度V，不利于后期的物料在料斗的流动。

2.2 凸弧段模型

凸弧段模型在曲线转运料斗设计中，主要用来约束物料在料斗内的运动，如挡料板的上半部分，凸弧段模型使物料沿切向运动。凸弧段模型速度的计算，其目的不仅是为更好控制物料的速度，减少物料对料斗的冲击，还是决定相切下一段的初速度的数值。

2.2.1 模型计算

图4所示为物料冲入凸弧段模型时受力情况，凸弧段模型计算时，保证散状物料运动过程中不能脱离料斗壁，沿料斗壁运动，即料斗壁对物料的反力FN大于零。凸弧段模型理论计算为

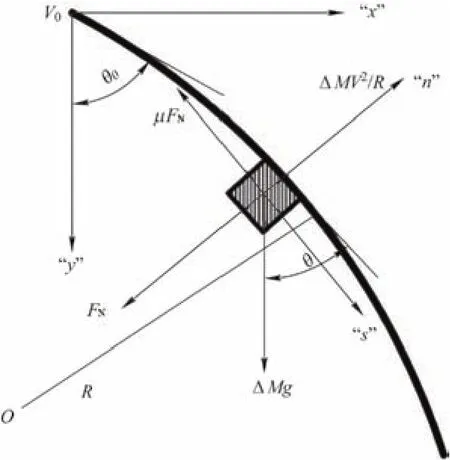
图4 凸弧段模型

凸弧段理论模型任一点的速度为

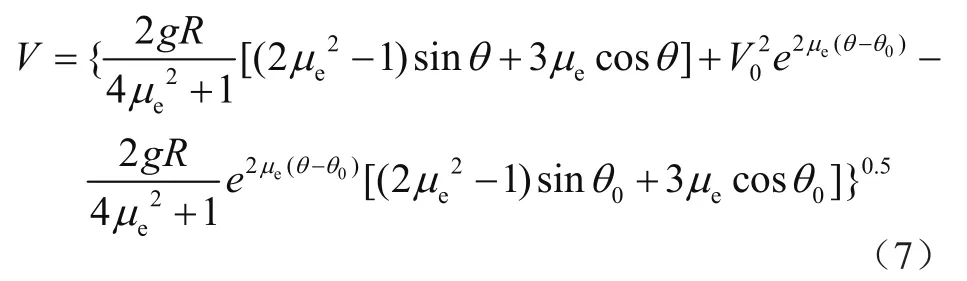
2.2.2 变量分析

料斗凸弧段设计主要有曲率半径R和角度（料斗壁内任一点速度切向与竖直方向夹角）θ决定。为更好研究两者对计算速度V的影响，假定等效摩擦系数μe为0.4，初始角度（料斗壁起点速度切向与竖直方向夹角）θ0为90°，初始速度V0为8 m/s，变量分析如图5所示。

图5 计算速度V与曲率半径R、角度θ关系曲面

如图5所示，当曲率半径R为2 m，角度θ逐渐减小时，计算速度由8 m/s减小至7.18 m/s，随着曲率半径增大，计算速度V逐渐增大，重力势能逐渐优于摩擦力做的功，如R为6 m时，计算速度V由8 m/s增大至10.87 m/s。同理，当角度θ为90°时，表明物料在凸弧段初始点，计算速度V即是初始速度V0，速度梯度变化为0。随着角度θ的减小，计算速度V因曲率半径变化产生波动性变化，但速度梯度变化随曲率半径增大而逐渐增大，当角度为0°时，计算速度由7.18 m/s增大至10.87 m/s。因此，在料斗凸弧段曲率半径R、角度θ的设计中，在保证计算速度V的情况下，综合考虑二者之间的相互影响。不同半径下角度 -速度关系曲线、不同角度下半径 -速度关系曲线如图6所示。

图6 关系曲线图

2.3 凹弧段模型

凹弧段模型同凸弧段模型一样，主要用以约束物料在料斗内的运动速度的大小和方向。如应用在给料匙，凹弧段模型速度的计算即可避免堵料又可减少物料对接料输送带的冲击。

3.3.1 模型计算

如图7凹弧段模型所示，理论计算为

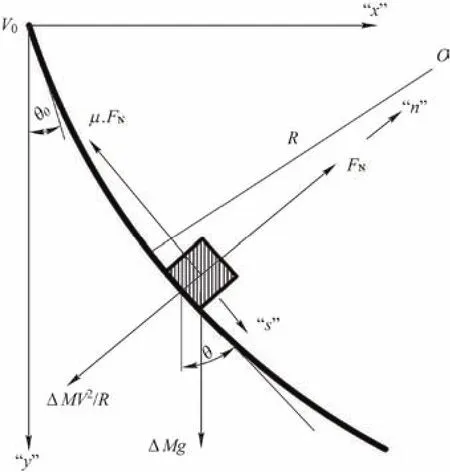
图7 凹弧段模型

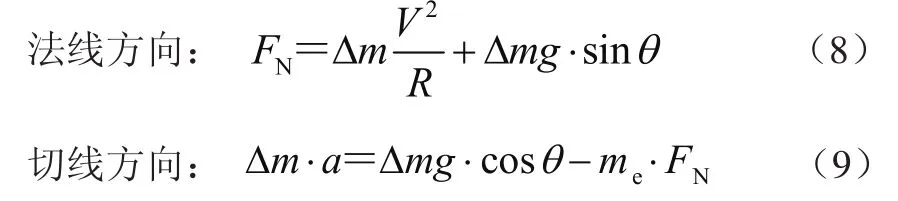
根据凸弧段相似原理微分方程计算，凹弧段理论模型任一点的速度为

2.3.2 变量分析

料斗凹弧段设计主要由曲率半径R和角度（料斗壁内任一点速度切向与竖直方向夹角）θ决定。为更好研究二者对计算速度V的影响，假定等效摩擦系数μe为0.4，初始角度（料斗壁起点速度切向与竖直方向夹角）θ0为0°，初始速度V0为 8 m/s，变量分析如图8所示。不同半径下角度 -速度关系曲线与不同半径下角度 -速度关系曲线如图9所示。

图8 计算速度与曲率半径、角度关系曲面

图9 关系曲线图

曲率半径R为2 m时，随着角度θ的增大，计算速度V逐渐减小至5.13 m/s，表明物料流动过程中，摩擦力做的功优于重力势能。随曲率半径的增大，计算速度在0°～ 90°范围呈现先增大后减少的趋势，曲率半径为6 m时，计算速度由8 m/s增大至9.22 m/s，再减少至6.52 m/s。同时，当角度θ为0°时，表明物料在凹弧段初始点，计算速度V即是初始速度V0，为8 m/s，速度梯度变化为0。随着角度θ的增大，计算速度V因曲率半径变化产生波动性变化，但速度梯度变化随曲率半径的增大而先增大后减小。同样，在料斗凹弧段曲率半径R、角度θ的设计中，要综合考虑二者之间的相互影响。

2.4 抛料模型

抛料模型同迎料点、凸弧段、凹弧段模型不同，物料以一定的初速度斜向抛出，物体作匀变速曲线运动，其运动轨迹是抛物线，自由抛料不受转运料斗的约束，主要集中在物料离开给料输送带的抛物线运动和物料离开挡料板进入抛物线运动。抛料模型如图10所示，速度理论计算为

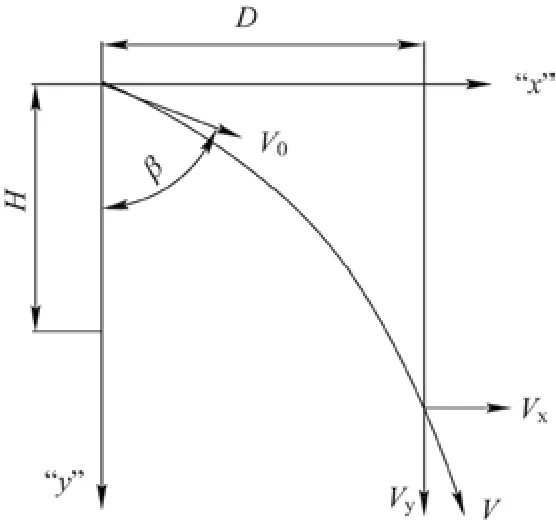
图10 抛料模型

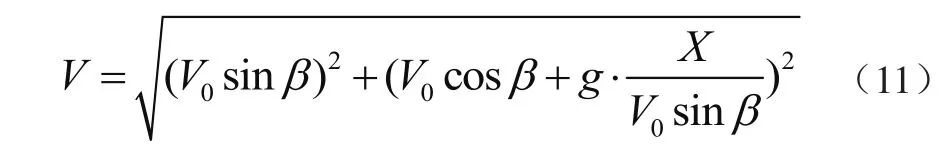
式中：X为水平距离，β为初速度角。

由理论计算可知，在初速度V0为定值时，抛料模型的速度V是由初速度角度θ0及水平距离X（或与之相对应垂直距离H）决定[6]，其关系曲线如图11所示。初速度为6 m/s，X为1 m时，在初速度角度θ0（10°～170°）范围内，随着角度的增大，速度V呈现由先减小后增大的趋势，主要是物料的抛料时间t来决定的，水平速度V0sinθ0与抛料时间成反比的关系。同时，随着水平距离X增大，速度V整体向上移动。X为3 m、θ0为10°时，速度V达到45 m/s。

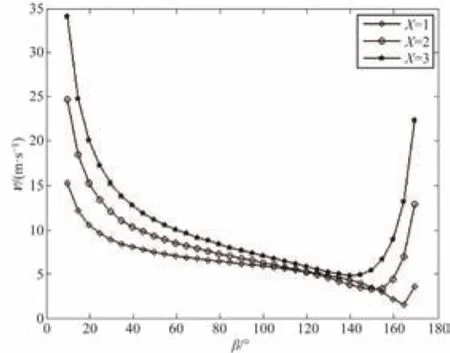
图11 不同水平距离下角度-速度关系曲线

3 模型验证

根据工程项目的实际应用进行模型验证，基于连续模型理论进行曲线料斗快速设计。设计输入物料为精矿粉；设计运量Q=800 t/h，带宽B=1.2 m，输送带带速V=2 m/s；落料高度H为6.5 m。由于物料流动性较差，取等效摩擦系数μe为0.5；头部滚筒直径1 m，物料堆密度为0.85～1.1 t/m3。

曲线料斗物料转运自上而下的顺序分别为物料脱离头部滚筒抛料；挡料板（直线段、凸弧段、凹弧段构成）挡料；物料脱离挡料板抛料；给料匙（直线段和凹弧段）送料。由于输送带为2 m/s，在曲线转运料斗快速设计中，不仅要保证物料速度变化平稳，以减少物料对料斗的冲击和磨损，还要保证给料匙出口物料的速度应等于或略大于输送带的速度，以实现物料有效通过量的转运。

理论设计计算参数如图12所示。物料脱离头部滚筒抛料：β=43°、X=1.3 m、V=3.21 m/s；挡料板直线段迎料点：α=25°、V=1.96 m/s；凸弧段 1：θ0=18°、θ=8 °、Δθ=10 °、R=3 m、V=2.68 m/s； 凸 弧 段 2：θ0=8°、θ=0°、Δθ=8°、R=2.4 m、V=2.90 m/s；凹弧段2：θ0=0°、θ=30°、Δθ=30°、R=2 m、V=2.88 m/s；物料脱离挡料板抛料：β=0°、X=0.9 m、V=4.12 m/s；给料匙直线段迎料点：α=24°、V=2.61 m/s;凹弧段：θ0=5°、θ=60°、Δθ=55°、R=2.1 m、V=2.21 m/s。

图12 曲线料斗理论设计

工程实践运行与理论计算较为吻合，出口物料综合平均速度测量为2.16 m/s，误差在允许接受范围内，仅为2.3%。结果证明，该理论设计方法简单有效，在工期较为紧张的情况下，有效地节约了时间，最重要的是避免了转运系统中堵料和喷粉的发生，有效地保证了输送系统的连续性。

4 结论

建立基于连续模型理论建立曲线转运料斗理论设计方法，该方法包括建立相应的迎料点冲击模型、凸弧段模型，凹弧段模型、抛料模型，并推导各模型下计算速度V的理论计算公式，分析各模型因素对计算速度V的影响，最后通过工程实例验证曲线料斗的理论设计的合理和有效性。同时，曲线料斗设计进一步的工作还要继续研究，如研究随高度H的增大，除挡料板、给料匙外，曲线料斗的中间分段和位置规律；料斗的横截面形状、物料特性对曲线转运料斗理论设计方法的影响；散料在料斗中的速度对产生粉尘气体浓度的影响等，这些将是继续研究的方向。