压电驱动器的率相关迟滞特性建模与测试

张段芹，冯炳昊，曹 宁，刘 嘉，聂 晶

(1.郑州轻工业大学 机电工程学院，河南 郑州 450002;2.郑州轻工业大学 计算机与通信工程学院，河南 郑州 450002；3.北京航空航天大学 前沿科学技术创新研究院，北京 100191)

0 引言

压电陶瓷具有体积小，结构简单，分辨率高，出力大，结构紧凑，响应速度快等优点，常用于微纳米定位系统，广泛应用于超精密机械、精密仪器制造、生物医疗器械及半导体制备等领域[1]。由于压电陶瓷迟滞非线性特性严重降低了其定位精度和稳定性等性能，因此，深入研究或补偿压电陶瓷的迟滞非线性，提高其定位精度是目前研究的关键和热点问题[2]。

针对压电陶瓷的迟滞非线性对压电微定位台定位精度的影响，目前的主要研究方向是通过建立各种迟滞非线性的数学模型模拟压电陶瓷的迟滞输出特性[3]。常用的迟滞模型有Duhem模型[4]、Bouc-Wen模型[5]、Preisach模型[6]、经典Prandtc-Ishlinskii(P-I)模型[7]、Maxwell滑动模型[8]及神经网络模型[9]等。P-I模型采用一重积分，因其具有简单的数学形式，需辨识参数相对较少，特别是求解其逆模型或近似逆模型相对容易，故被广泛应用于压电陶瓷的迟滞建模[10]。随着对压电陶瓷的深入研究发现，压电执行器中具有率相关特性，而这些模型大多数不能描述压电陶瓷的率相关特性[11]。基于此，文献[11]建立具有动态权值、阈值的P-I模型来描述率相关迟滞非线性。文献[12]引入二次多项式和初始位移项，描述压电陶瓷迟滞静态非线性特性，通过把输入信号频率引入模型参数，实现了对压电陶瓷迟滞动态特性的直接描述。本文通过引入电压变化率，提出率相关的迟滞模型，首先通过引入多项式来描述压电陶瓷迟滞静态非线性特性；在静态迟滞模型基础上，通过将电压升降速率引入模型参数以描述压电陶瓷的速率相关特性。

1 率无关的P-I模型

采用双边Play算子的经典P-I模型[13]来描述压电陶瓷迟滞非线性特性，从数学上讲，经典P-I模型可以描述为

(1)

式中：t为时间；y(t)，v(t)分别为模型的输出位移和输入电压；p0为系数；pi为对应阈值ri(1≤i≤N)的迟滞算子权重系数；Fri[v](t)为输出位移的迟滞算子。其中：

Fri[v](0)=fri(v(0),0)

(2)

Fri[v](t)=fri(v(t),Fri[v](t-T))

(3)

fri(v(t),w(t))=max(v(t)-ri,min(v(t)+

ri,w(t)))

(4)

式中T为采样周期。

如图1所示，在输入非负电压的情况下，双边Play算子形成的滞环不随控制输入返回到0，初始加载曲线(双边Play算子驱动电压从0施加到最高值的升程曲线，其初始输出位移为0)外的后续轨迹具有初始位移，这种特性与压电驱动器的特性非常相似。

图1 双边算子电压位移图

考虑到经典P-I模型只能模拟中心对称的迟滞曲线，而压电陶瓷的迟滞曲线为中心非对称，所以提出修正的P-I模型通过引入多项式来模拟压电驱动器的迟滞非线性曲线，有：

(5)

g(v(t))=a1v(t)+a2v(t)2+a3v(t)3

(6)

式中a1、a2、a3为常数项系数。

2 率相关的P-I模型

上述提到的P-I模型是与速率无关的模型，率无关的P-I模型常用于描述陶瓷在低频时的迟滞现象。当频率增加时，由于压电陶瓷的迟滞率与频率有很强的相关性，使用这些滞环模型会引起较大误差，因此有必要建立一个速率相关的P-I模型。

在率无关模型的基础上将输入电压升降速率引入动态迟滞模型参数中，用于描述压电驱动器率相关的迟滞非线性，表达式如下：

(7)

(8)

3 实验

压电陶瓷驱动器的率相关输出位移测试平台的硬件组成原理如图2所示。计算机产生驱动指令，经数据采集卡的数模转换(D/A)输出模拟信号，再经功率放大驱动压电驱动器，驱动位移经位移传感器传至数据采集卡模拟输入端，经模数转换(A/D)到计算机。各组件的主要参数如下：叠堆式压电驱动器在输入电压0～150 V内的输出位移为0～12 μm；功率放大器采用芯明天公司生产的型号为E03.00压电驱动电源，带宽为1 kHz；位移检测采用德国米铱公司的电容式非接触位移传感器，分辨率为20 nm，带宽为5 kHz；采用的NI数据采集卡最大输出更新率为2.8 MS/s，最大输入采样率为1.25 MS/s。实验台实物图如图3所示。

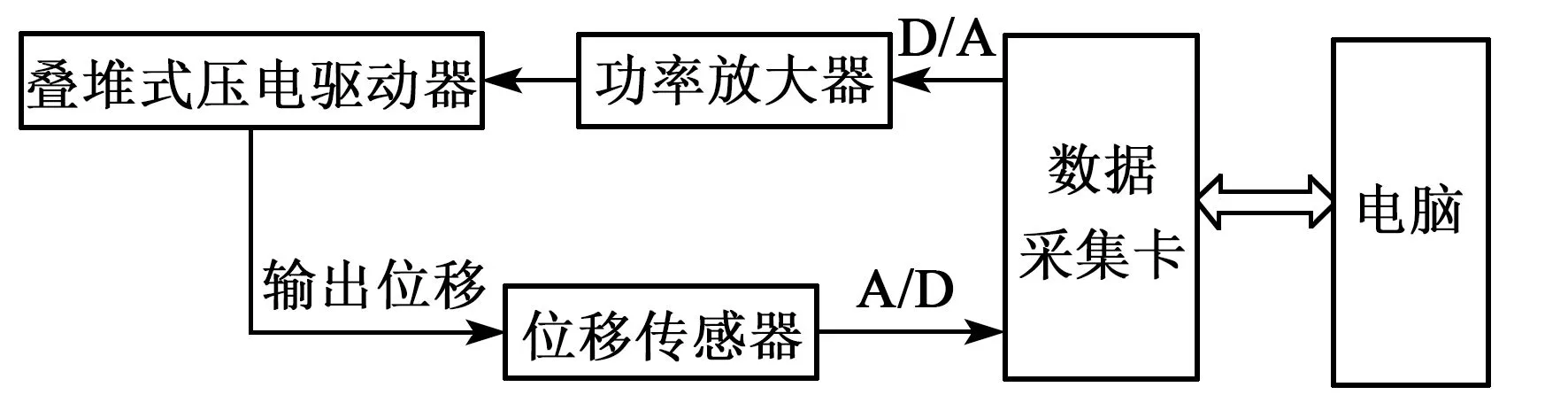
图2 硬件组成原理图

图3 实验台实物图

利用Labview编程产生三角波信号，上升和下降过程的采样数均为50个，给压电平台施加不同的电压速率(0.12 V/ms(1 Hz)，1.2 V/ms(10 Hz)，3 V/ms(25 Hz)，6 V/ms(50 Hz))、幅值30 V、偏置30 V的三角波电压信号，传感器信号采样率为2 kHz。从计算机产生驱动信号到计算机采集到位移信号具有一定的时间滞后，需要测量除压电驱动器本身的响应滞后外的附加滞后，附加滞后包括D/A转换与保持、采样与保持、A/D转换信号处理滞后以及功率放大和位移传感器的滞后。通过同时采集模拟输出信号，获得附加滞后时间约为13 ms。处理数据时需考虑附加滞后的时间，由于实验中的压电陶瓷驱动器未加负载，在高频使用时惯性力会变大并在内部产生拉伸应力，破坏压电材料，因此，为了保护叠堆式压电陶瓷驱动器，施加的信号频率最高为50 Hz。

压电驱动器在不同驱动频率下的输出位移如图4所示。随着输入信号频率的不断增大，对应的迟滞环也越来越宽，迟滞环在电压最大时的位移逐渐减小，迟滞环表现出率相关的特性。

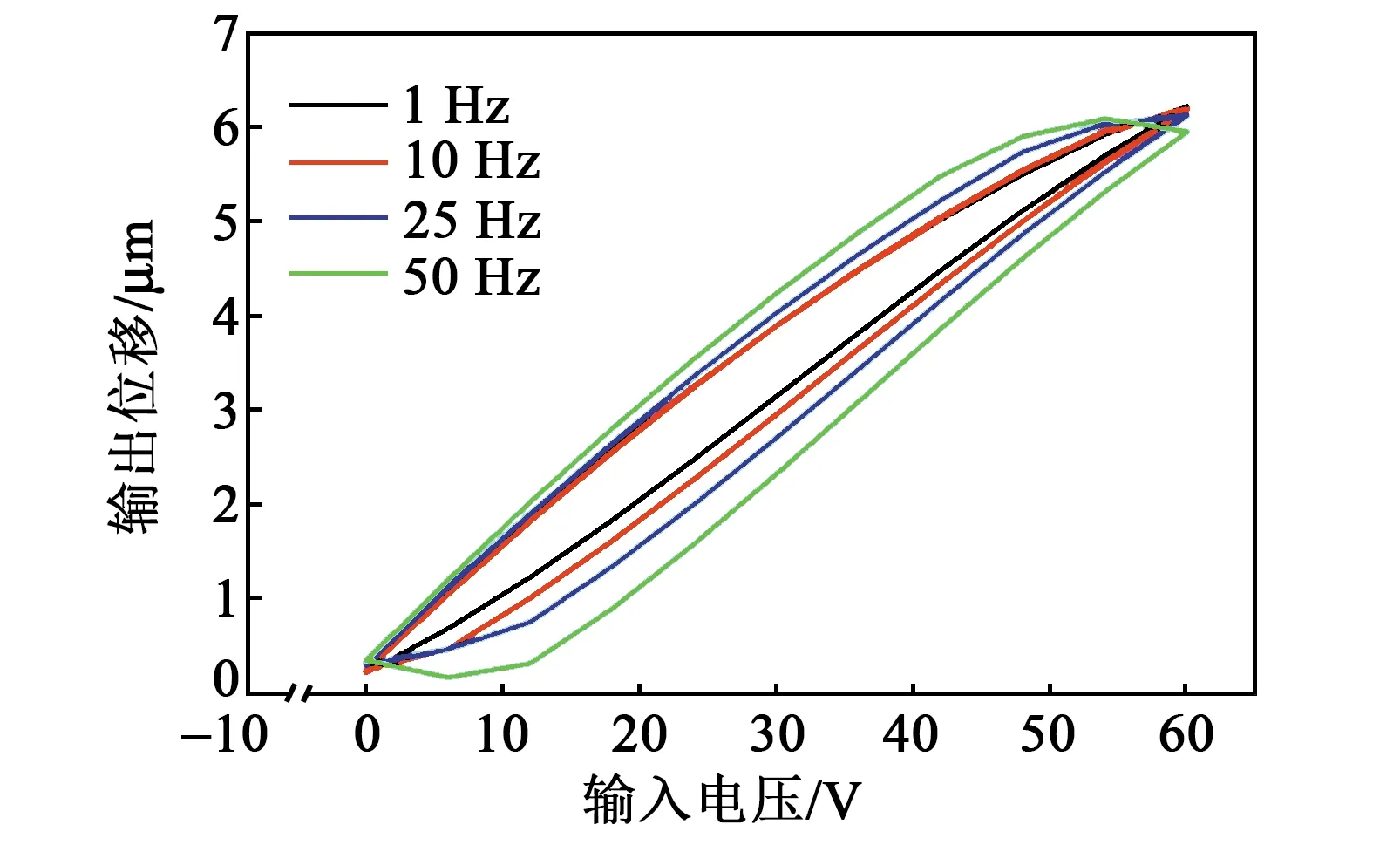
图4 压电驱动器在不同频率输入信号下的迟滞曲线

4 参数辨识及模型验证

4.1 参数辨识

根据式(7)的率相关模型，需要辨识的模型参数有a1、a2、a3、a4及每个算子的权值。为了简化动态迟滞模型，方便分析不同输入信号施加电压速率与对应的动态模型之间的关系，设置所有模型中的权重系数和阈值均保持一致。阈值可由下式确定：

(9)

式中N为迟滞算子的数量。利用测得的数据使误差最小化，通过调用MATLAB优化工具箱中最小二乘法辨识不同频率下的模型参数，表达式为

(10)

式中：ψ(k)为模型输出位移；e(k)为最小化误差。以速率为0.12 V/ms(1 Hz)的三角波输入信号为参考信号辨识率相关时的算子权重系数和模型参数，数据如表1所示。表2为不同速率下的模型参数。图5为不同速率下的模型参数曲线。

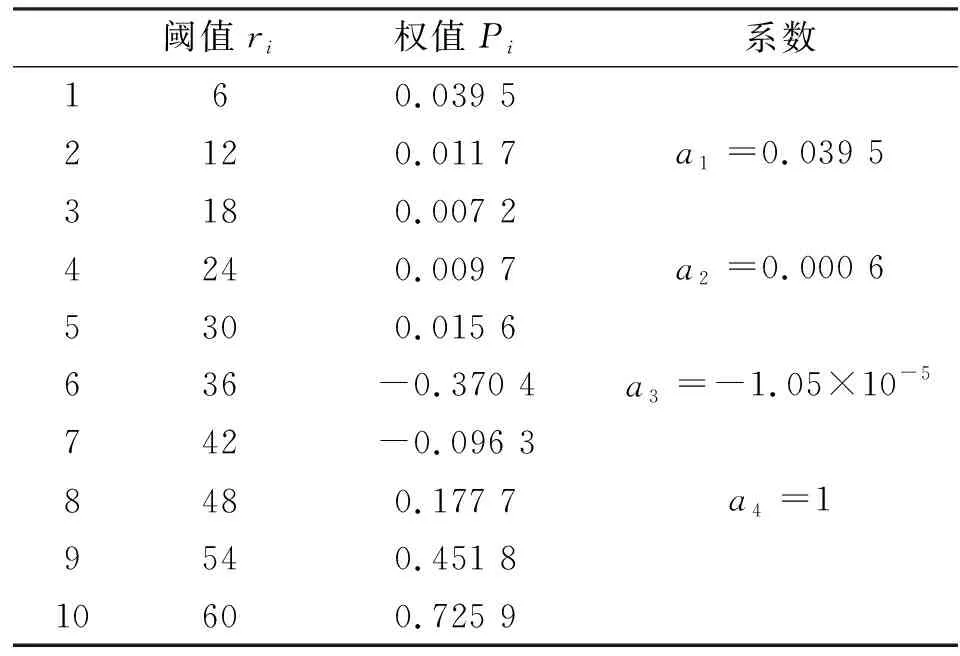
表1 率相关的算子权重系数及模型参数

表2 不同速率的模型参数

图5 不同速率下的a1，a2，a3，a4模型参数曲线

由图5可见，模型参数与速率呈近似线性关系，可以用一次函数关系来表达：

(11)

(12)

(13)

(14)

利用MATLAB最小二乘法进行曲线拟合辨识动态模型参数k1，k2，k3，k4，k5，k6，k7，k8，如表3所示。

表3 动态模型参数

4.2 模型验证

给压电平台施加幅值30 V、速率4.8 V/ms(40 Hz)、偏置30 V的三角波电压信号进行模型验证。利用0.12 V/ms建模数据并借助辨识的模型参数k1～k8，得出不同速率实测模型与建模模型的对比图如图6所示。

图6 不同速率实验结果与仿真结果对比及误差曲线

为了验证所建模型的准确性，本文采用均方根误差ERMS作为验证准确性的指标。

(15)

式中：n为采样数据个数；y(i)为采集到的压电陶瓷微定位平台实际位移输出；ym(i)为模型预测输出。表4为不同速率模型误差。

表4 率相关模型误差分析

由表4可见，在0.12～6 V/ms，模型最大误差控制在0.076～0.190 μm，均方根误差控制在0.044～0.077 μm，相对误差为1.2%～3.2%。由图6可见，随着输入施加电压速率的升高，最大位移误差、平均位移误差和均方根误差都有不同程度的升高，验证模型最大误差控制0.19 μm内。

5 结束语

本文提出了一种与速率相关的P-I模型，表征压电致动器的速率相关的迟滞非线性。首先通过引入多项式，描述压电陶瓷迟滞静态非对称性特性；在静态迟滞模型基础上，通过把速率引入模型参数以描述压电陶瓷的速率相关特性。利用不同速率的三角波输入测得响应位移，采用最小二乘法对模型参数进行辨识。模型误差相对较小，较好地拟合了压电陶瓷迟滞非线性的特性。