基于CMCPSO-SVM的轴承微弱故障诊断方法

纪俊卿，孔晓佳，邹方豪，张静，许同乐，袁伟

(山东理工大学机械工程学院，山东淄博 255049)

0 前言

轴承作为旋转机械的核心部件，其运行状态直接影响整个机械系统。据不完全统计，旋转机械轴承发生故障的概率是所有设备故障的30%。因此，对轴承的早期故障进行预防和处理，在工程安全问题上显得尤为重要。

近几年来，对于电机轴承故障诊断方面的研究越来越多，由于支持向量机(Support Vector Machines,SVM)有克服维数高和过拟合的特点，在轴承故障诊断领域被广泛应用，但是否能够准确地选择SVM中的惩罚因子与核函数参数将直接影响故障诊断模型的精度。因此，有学者采用粒子群(PSO)优化算法对SVM中的惩罚因子与核函数进行寻优，提高算法精度。唐贵基等通过快速谱相关以及PSO-SVM，建立一种有效的轴承状态识别算法。石志炜等利用改进PSO算法优化相关向量机，并应用于滚动轴承故障诊断。YAN和JIA将粒子群优化算法与支持向量机相结合，对多域的轴承故障特征进行分类识别，但由于PSO算法存在求解精度低和局部寻优的问题，应用率和准确率降低。

针对传统PSO算法优化SVM存在的问题，文献[5]中提出一种混沌粒子群(Chaotic Particle Swarm Optimization,CPSO)算法，利用混沌思想优化传统粒子群算法，并应用于滚动轴承故障诊断等领域。但是，由于混沌映射的混沌序列不收敛、非周期性等特性，导致粒子之间的交流并不充分，易陷入局部寻优和求解精度低的问题仍然存在。SON等提出了一种基于核支持向量机的自适应PSO算法，利用核支持向量机的自适应参数控制，提高改进PSO算法的收敛速度和搜索能力。WANG等将CPSO算法用来优化SVM，对航空电子导航系统的接收器轴承故障进行诊断，取得了较理想的效果。但由于粒子群之间交流不充分和搜索范围大等缺点，上述方法在实际工程中的诊断效果并不明显。

针对传统PSO算法优化SVM存在的问题，本文作者提出一种改进的混沌粒子群优化支持向量机，并将它用于旋转机械轴承故障诊断领域。采用混沌思想对进行PSO优化，加入自适应交叉和变异策略；以LMD分解PF分量的排列熵为新适应度函数；用改进粒子群算法优化SVM，构建新故障诊断模型。以型号6205-2RS故障轴承为例，证明新故障诊断模型准确性高于传统诊断模型。

1 改进混沌粒子群优化支持向量机

1.1 混沌粒子群算法介绍

假设种群中包含维的粒子，且粒子群的规模为，那么在种群中每个粒子的空间位置以及速度分别表示为

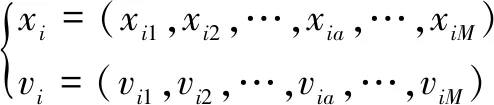
(1)

(2)

其中:代表惯性权重；和代表[0,1]的随机数；、分别代表自身学习权重系数和社会学习权重系数，且、∈[1.5,2]；代表第个粒子第个分量搜索的历史最佳寻优位置；g，代表全局寻优第个分量最佳位置。采用经典的Logistic方程构建混沌运动序列：

+1=(1-)

(3)

其中：为混沌系数；为样本个数。

混沌思想优化PSO算法主要是利用式(3)对惯性权重、自身和社会学习权重系数、等3个参量进行优化。另外，通过CPSO算法对传统PSO后期收敛速度慢以及易陷入局部寻优进行处理。但由于混沌映射存在混沌序列不收敛、非周期性等特性，在面对含有复杂干扰的样本时，仍然有极大可能陷入局部最优。因此，如何克服CPSO算法的混沌特性成为文中研究的重点。

1.2 自适应交叉变异混沌粒子群算法

本文作者针对上述CPSO算法缺点，提出一种交叉变异混沌粒子群算法(CMCPSO)，具体如下：

1.2.1 自适应交叉变异策略

(1)交叉策略

为增加粒子之间交流，随机选择一定数量的粒子按照交叉概率进行个体之间的交叉操作，使得交叉后的粒子代替原始粒子，保证粒子数目不变。既不增加粒子的复杂度，又完善了算法交流机制，达到寻找最优参数的目的。自适应交叉概率表达式如下：

(4)

其中:为常数，通常取1；为选取粒子群的最大适应度；为参加交叉粒子的适应度。

(2)变异策略

为使PSO算法在迭代过程中避免陷入局部最优，丰富粒子种类的多样性，加入一种自适应的变异策略，利用自适应交叉概率进行变异操作，极大地改善了种群单一的问题，增加其多样性。自适应变异概率表达式如下：

(5)

其中:为常数，且=05；′为参加变异粒子的适应度。

1.2.2 新的适应度函数

排列熵(PE)能够将系统中的不规则性和非线性以定量熟知的方法表达出来。由于排列熵能够迅速且准确地反映出系统特征，将利用LMD算法分解后得到的PF分量的排列熵作为粒子适应度函数。为了方便分析，对PE归一化处理获得新适应度函数：=/ln。排列熵计算公式为

(6)

其中：为第个频率幅值出现的概率；′为第个PF分量归一化处理的能量特征。

1.3 支持向量机理论

支持向量机是将一个集合的数据按照一定标准使类别之间距离最大化的一种线性分类器，是寻找最优超平面+=0的过程，使之尽可能正确地对正类和负类数据进行分类。核函数为SVM算法最重要的部分，且径向基核函数只需确定一个参数，则该函数的普适性高于其他函数。文中核函数选取高斯径向基函数(RBF)，公式如下：

(7)

由于径向基核函数只受参数影响，参数的选择直接影响SVM的分类精度。不同的RBF核参数分类效果也不同，随着参数的增大，数据分类边界与数据拟合更加贴合，边界形状也有不同。

1.4 改进混沌粒子群优化支持向量机流程

SVM中最核心部分就是惩罚因子与参数，该参数优化程度直接决定SVM分类正确率。本文作者利用一种交叉变异混沌粒子群优化支持向量机，建立一种新的分类模型(CMCPSO-SVM)，详细流程如图1所示。

图1 改进混沌粒子群优化支持向量机流程

2 滚动轴承故障分类过程

传统SVM分类算法具有正确率低、收敛速度慢等缺点，以传统PSO算法为基础，提出一种新的交叉变异混沌粒子群优化支持向量机算法CMCPSO-SVM，具体过程如下：

(1)滚动轴承故障特征提取

利用LMD对轴承故障信号进行分解，最终得到有效信号PF分量并对它进行归一化处理。处理步骤如下：

①求出各个分量PF,的总能量:

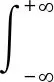
(8)

②将充当特征矩阵的元素，如式(9)所示：

=[,,,…,]

(9)

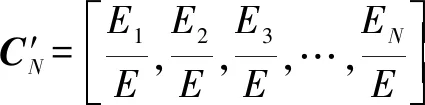
(10)

(2)故障特征的选择

LMD分解得到的原始特征向量维数较高，直接进行分类识别计算量大且精度不高。迭代拉普拉斯分数(ILS)是一种新颖有效的特征选择方法，它在传统的拉普拉斯分数算法基础上，通过局部保持来确保每次迭代中剔除最不相关特征,逐渐更新近邻图，根据每个候选特征的重要性来评估和选择有意义的敏感特征子集。因此，文中选取ILS对滚动轴承故障数据进行降维，建立低维故障特征集。

(3)CMCPSO-SVM故障分类模型的建立

采用交叉变异混沌粒子群算法,按照第1.4节的方法对SVM进行优化，建立新的CMCPSO-SVM轴承故障分类模型。将滚动轴承的训练样本与待测样本分别通过步骤(1)(2)进行故障特征集的建立，并分别作为训练集和测试集输入CMCPSO-SVM分类模型，计算适应度值，输出故障分类结果。轴承故障诊断总体流程如图2所示。

图2 轴承故障诊断总体流程

3 实验验证

为验证CMCPSO-SVM故障分类模型的优越性，以型号为6205-2RS的深沟球故障轴承搭载平台进行轴承故障诊断实验，实验台结构如图3所示。实验台由IEPE磁吸压电式加速度传感器(DH187和DH131)、异步电机、联轴器、减速箱、轴承等组成，电机转速为600 r/min、采样频率为12 800 Hz、采样点数为4 096。利用文献[15]中的方法对信号进行降噪处理，图4所示为降噪重组后振动信号时域图。

图3 实验台结构

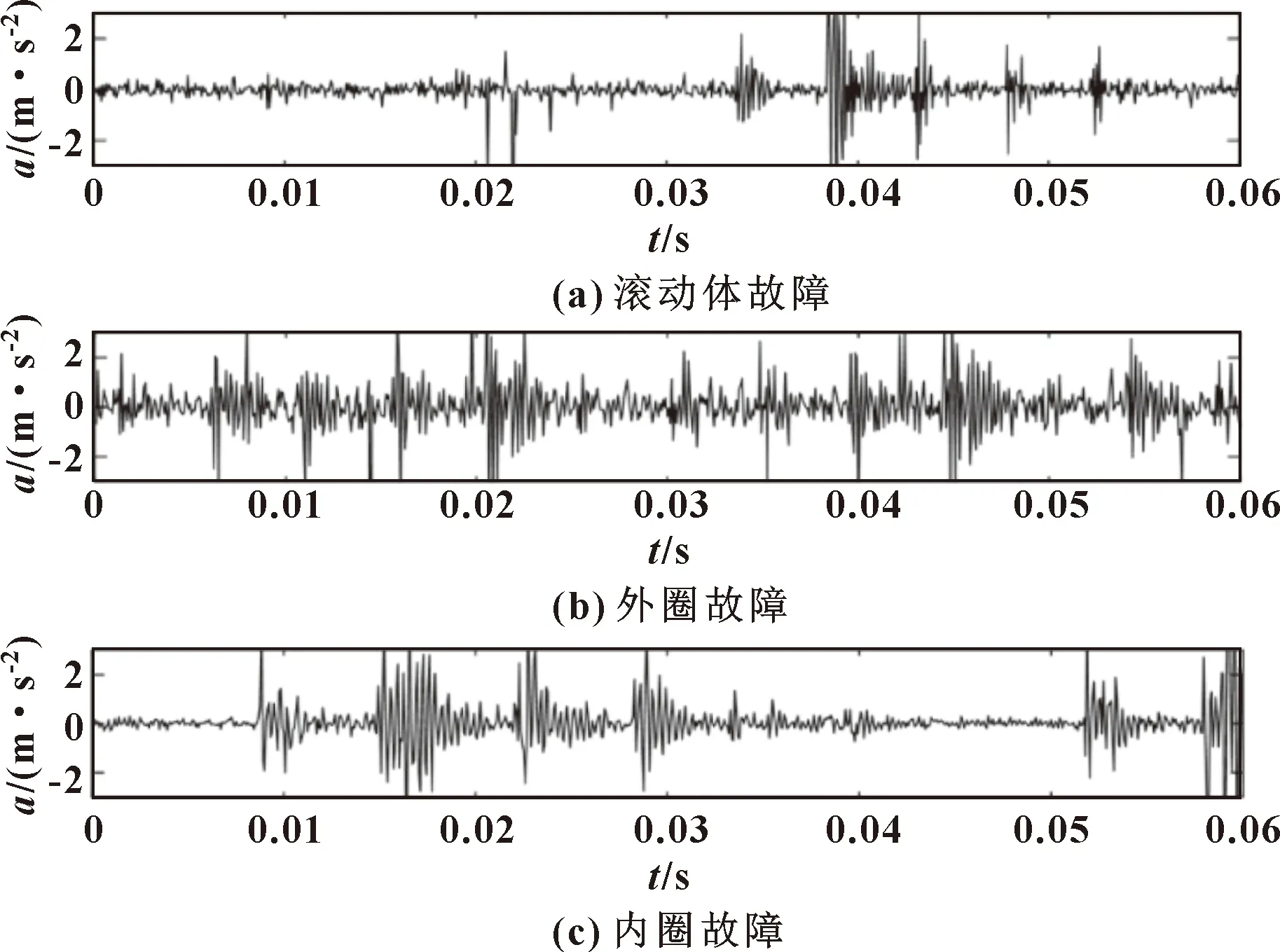
图4 降噪重组后信号的时域

步骤1：为了方便分析，将3组原信号中内圈、外圈以及滚动体故障分别记作IR、OR和BR。首先，将每种工况下的前409 600个采样点平均分为400组，每组含有1 024个样本，且保证样本不重复；其次，分解三类源故障信号LMD，并按照式(10)进行归一化处理；最后，为保证特征集的丰富性、提高容错率，将400组样本随机分成40个故障特征集，每个特征集中包含80个特征值。3种工况共得到120个特征集，组成的特征向量矩阵。表1所示为能量归一化结果。

步骤2：为避免样本集合之间的连续性，随机选取每个故障类型的20组特征集充当训练集，另外20组当作测试集。利用ILS算法对原始训练集中所有特征值按照重要性排序，特征向量的得分计算方法见文献[16]。选取重要性高的特征组成低维特征集，实现对故障特征的降维处理，排序前后故障特征重要性顺序如图5所示。可知：排序前中每种工况原始的故障特征值非常相近，并不能够对冗余特征进行剔除，计算量大且错误率高；特征向量经过ILS算法处理后(排序后)，特征之间产生较大差异，能够很好地区分特征向量的重要性。本文作者选取前9个重要特征组成故障低维特征集。选取特征值重要性如下所示：

>>>>>>>>

其中:为第个特征向量的得分，得分越高说明对应的特征值越重要。

表1 LMD分解能量归一化结果

图5 排序前后故障特征重要性顺序

图6 不同分类模型适应度随迭代次数的变化

步骤3：按照第1.4节中改进混沌粒子群优化支持向量机，建立新的CMCPSO-SVM故障分类模型，并将训练集输入到分类模型中进行训练。其中，初始参数设定为：自身和社会学习权重系数==1.5，最大权重=09，最小权重=04，最大迭代次数为100次，=10、=05。图6所示为不同分类模型适应度随迭代次数的变化，可发现：在不同的优化算法下，CMCPSO算法在30次内收敛，这说明新的寻优算法由于交叉变异策略，避免局部寻优过程，减少了收敛时间。与其他算法相比，尤其是传统PSO算法，文中算法的适应度值更加接近期望值。

利用结束训练的CMCPSO-SVM模型对待测故障特征集进行分类识别，根据输出结果判断滚动轴承的故障类型。为了证明文中故障分类器的优越性，将PSO-SVM、CPSO-SVM、IPSO-SVM分类模型与CMCPSO-SVM分类模型对比。图7所示为不同分类模型的故障分类结果，其中标签1、2、3分别表示滚动体、外圈、内圈故障。表2所示为不同优化算法SVM模型的诊断正确率。

由图7可以发现：PSO-SVM、CPSO-SVM和IPSO-SVM分类器实际的故障分类与预测输出存在较大差异，而CMCPSO-SVM分类模型预期输出与实际输出一样，分类精度达到90%以上，均优于其他分类器。由表2可知：对于不同的轴承故障类型，CMCPSO-SVM分类器分类效果最准确，平均正确率为95%；传统PSO-SVM故障诊断精度最低，平均分类正确率仅为75%，且其他两种故障分类模型虽然一定程度上提高了分类精度，仍不能够保证分类识别的准确率；从运行时间可以看出，除PSO-SVM分类器外，其余3种分类器运行时间相差不大，大多在50～55 s之间。证明CMCPSO-SVM分类模型能在保证运行时间合理的前提下，提高分类精度。

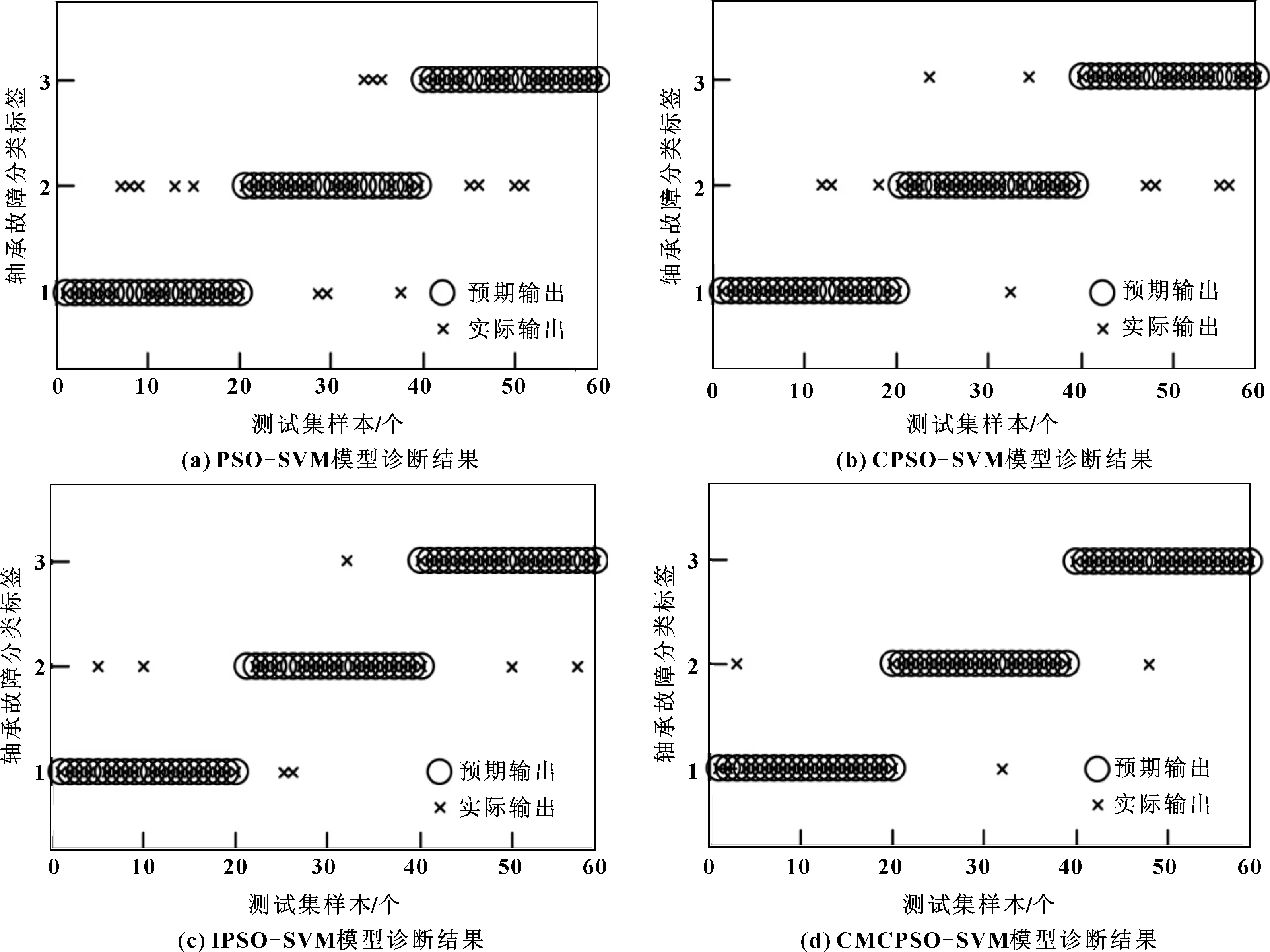
图7 不同诊断模型分类结果

表2 不同优化算法SVM分类器的分类准确率

在实际工程中需要平衡诊断精度与时间的关系，图8所示为ILS算法选取1～15个特征向量的分类精度与时间的关系。可以看出：当ILS算法选取9个特征向量时，诊断精度上升，收敛时间减少，保证了分类精度与收敛时间的平衡，更适用早期轴承故障诊断。

图8 不同特征数目的分类精度与时间

由于分类器的种类有很多，只在SVM分类器之间进行实验对比不足以说明CMCPSO-SVM分类器的优越性。本文作者根据以往经验，选取RBF神经网络、BP神经网络(BPNN)、K最近邻分类算法(KNN)、极限学习机(ELM)及CMCPSO-SVM算法对上述不同轴承故障的数据集进行故障诊断准确率的计算，结果如图9所示。可知：无论对于内圈、外圈和滚动体故障，CMCPSO-SVM算法的故障诊断正确率均保持在90%以上，高于传统RBF算法约9%，同时也优于BPNN、KNN及ELM算法，说明CMCPSO-SVM算法可靠性更高，为应用于实际工程奠定基础。

图9 不同分类算法的故障诊断准确率

4 结论

(1)利用迭代拉普拉斯得分降低原始特征集的空间维度。利用ILS算法对LMD分解得到的原始特征集按照重要性进行排序，选取前9个重要的特征向量组成低维特征集，减少分类模型的计算量。

(2)利用改进混沌粒子群对传统SVM诊断模型进行优化。在传统CPSO的基础上，加入一种新的交叉变异策略，丰富种群的多样性，尽可能使算法跳出局部寻优。同时,将LMD分解后得到的PF分量的排列熵作为新的适应度函数，提高CPSO算法的寻优能力。

(3)利用不同算法进行实验对比。以实际的风机发电机故障轴承为例，利用CMCPSO-SVM分类器对其故障进行诊断。结果表明：CMCPSO-SVM诊断准确率在90%以上，高于其他3种故障诊断模型。