绳驱超冗余机械臂结构设计与力学分析
耿浩,郭忠峰
(沈阳工业大学,辽宁省智能制造与工业机器人重点实验室,辽宁沈阳110870)
0 前言
传统工业机械臂在一些狭小的非结构化空间内进行作业非常困难,而超冗余机械臂作为一种特种机械臂,其关节空间维度远多于任务空间维度,能够满足作业时的位姿要求,广泛应用于对航空航天、核电站等非结构化的复杂狭窄空间进行探测、检修、救援等作业。
英国OC机器人公司研制的超冗余机械臂已经广泛应用在核电站、飞机装配等商业领域。刘天亮在2016年研制了一款超冗余机械臂,主要由10个连杆构成,具有20个自由度,运行非常灵活。符海明于2018年研制了一款混合驱动的超冗余机械臂,其结构主要采用了“离散式刚性连杆+联动机构+绳索”的主动-被动混合驱动形式。汤磊等人在2016年研制的一款绳驱动超冗余机械臂具有24个自由度,驱动部分绳索与机械臂绳索的排布处于相同的位置,具有较高的传动效率。
本文作者在相关学者研究的基础上对超冗余机械臂进行机械结构改进并进行力学分析,在根部关节加装由电机-丝杠控制的可伸缩连杆,使机械臂整体能够沿水平方向移动;在每个连杆的绳索孔中加入滑轮以降低绳索与连杆的摩擦;对绳索受力进行仿真和理论计算,对受力最大的关节进行强度校核。
1 机械臂结构设计
1.1 机械臂整体结构设计
机械臂的整体结构如图1所示,主要由驱动部分与机械臂组成。机械臂从根部开始依次为伸缩杆、关节和连杆。驱动部分主要由电机与传动机构组成。每个连杆端部圆周方向均匀分布小孔用于通过绳索,通过后置驱动电机带动绳索拉伸从而控制连杆的偏转角度。

图1 机械臂整体结构
1.2 驱动部分设计
驱动部分包含4个驱动层,其中,第1、2、4层分别有5个驱动绳索电机,如图2所示;第3层则有3个驱动绳索电机及1个驱动伸缩杆电机。
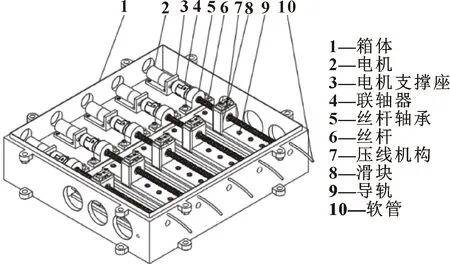
图2 驱动部分单层结构示意
单层驱动部分如图2所示,由电机控制丝杆的水平运动来驱动绳索拉伸,在丝杆的滑块上有一压线装置,其作用是通过调整压板把绳索压紧,外部软管作为绳索的导向回路,与端盖中绳索分布的18个小孔相连。
1.3 机械臂设计
机械臂由1个伸缩杆与5个连杆组成,连杆间通过万向节连接,伸缩杆位于机械臂根部,可使机械臂具有水平方向的自由度。每个连杆长为140 mm、直径为60 mm,2个连杆之间距离为16 mm,伸缩杆可伸出的最大长度为150 mm。当伸缩杆完全伸出时,机械臂最大可伸展长度为1 135 mm。为减小机械臂的整体质量,关节采用高强度铝合金7050-T7451。
机械臂连杆连接如图3所示。

图3 连杆连接示意
图4所示为单个连杆剖视图,单个连杆主要由2个端盘与1个空心筒体组成,在端盘与中心筒体周围分布穿绳孔,孔内装有2个滑轮,绳索穿过2个滑轮,减少绳索与连杆之间的摩擦,提高了绳索的寿命。

图4 单个连杆剖视图
机械臂伸缩杆剖视图如图5所示,通过电机-丝杆连接到伸缩杆的螺纹孔,从而控制伸缩杆的水平移动。伸缩杆前端由2个盖板与滑轮组成,通过螺栓连接。
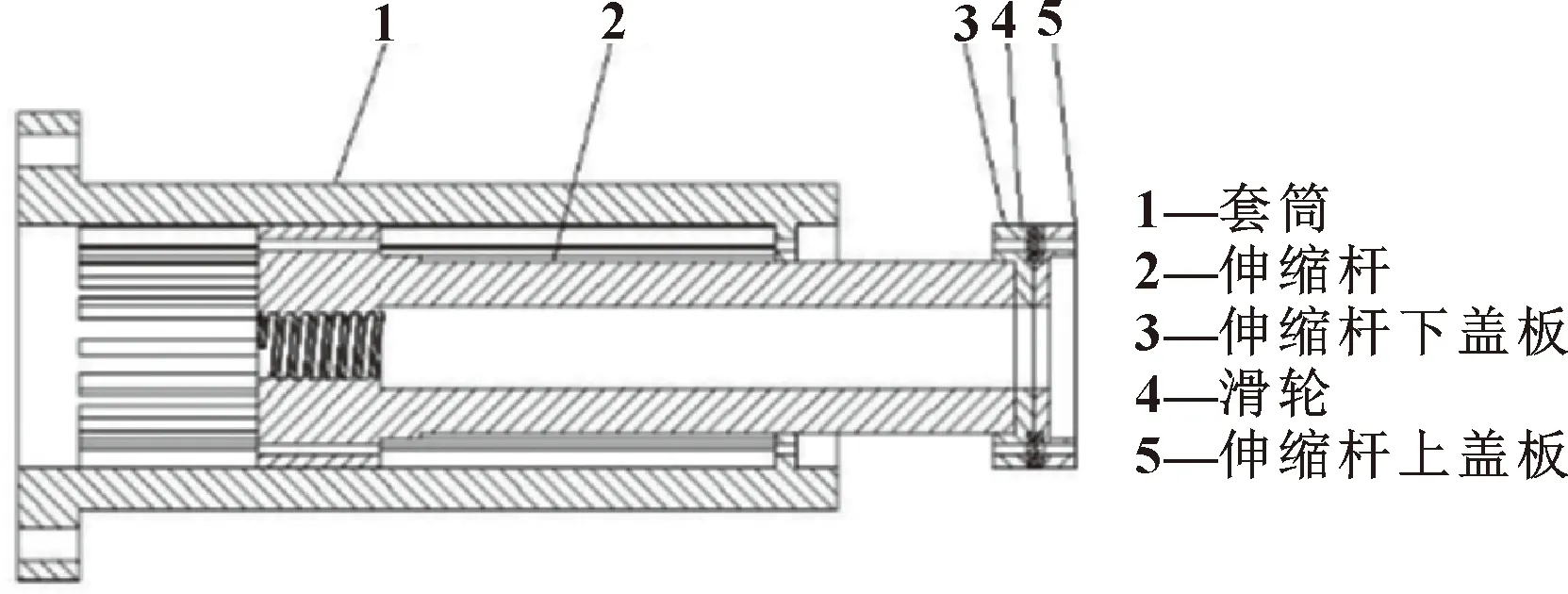
图5 伸缩杆剖视图
2 机械臂静力学分析
2.1 机械臂瞬态分析
通过ADAMS对机械臂进行瞬态分析,可以分析机械臂动态受力变化情况。对机械臂末端2个关节进行分析,机械臂的ADAMS模型如图6所示。
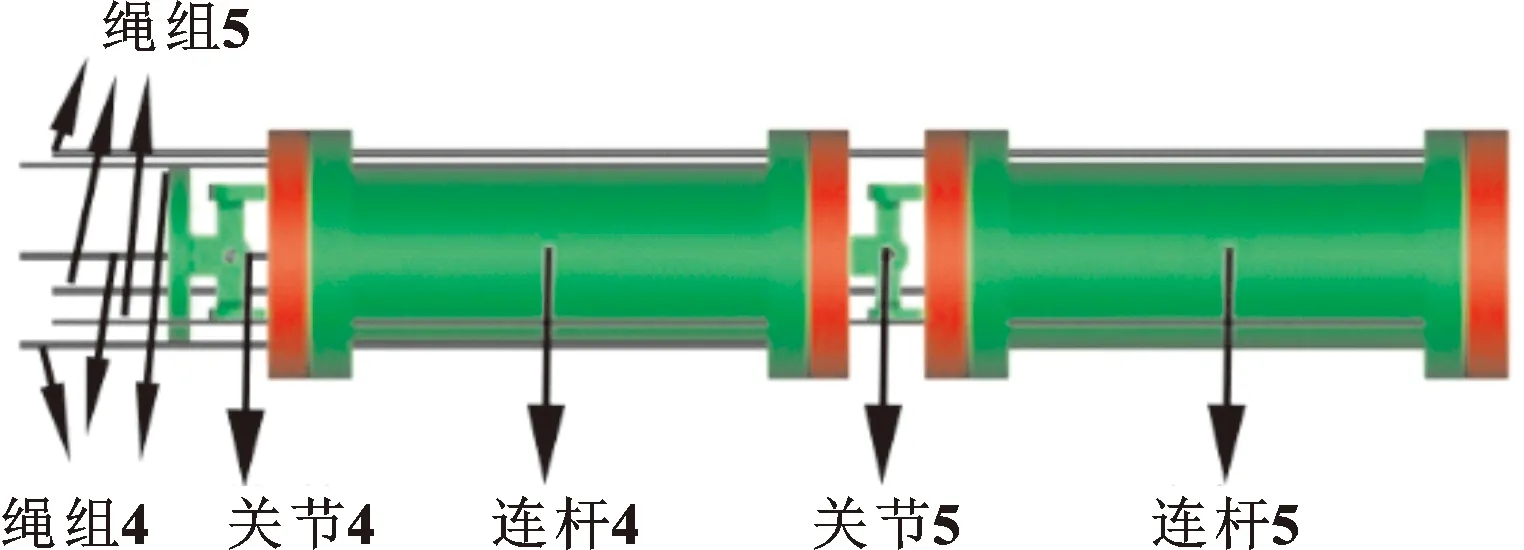
图6 超冗余机械臂运动学模型
机器臂瞬态分析的难点在于对绳索的仿真,本文作者采用对柱状体添加轴套力的方法来模拟绳索。在仿真时绳索的一端与关节端部固定,另一端与大地固定。在机械臂端部添加与重力方向一致的外力,为一个随时间变化的二次方的函数力,变化范围为0~20 N,用时5 s,步数为2 000步,对机械臂进行仿真。
绳组4与绳组5的受力情况分别如图7、图8所示。

图7 绳组4受力情况 图8 绳组5受力情况
由图7、图8可知:前2 s内绳索的受力情况不稳定,2 s后绳索受力随着时间的变化呈一个稳定上升与稳定下降的趋势,其中绳子受拉为正,受压为负。4-1、4-2、4-3、5-1、5-2、5-3号绳在第5 s时受到的作用力分别为147.6、152.1、-36.44、71.2、117.9、-33.99 N。
2个关节受力情况分别如图9、图10所示。
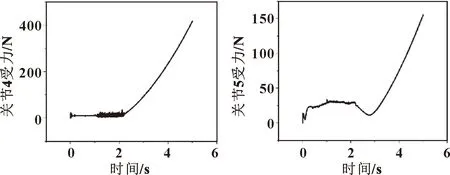
图9 关节4受力情况 图10 关节5受力情况
由图9、图10可知:前2 s关节受力处于不稳定状态,2 s后随着时间的变化关节受力稳定上升;关节4在第5 s时受到的力为418 N,关节4受力加起来为418.37 N;关节5在第5 s时受力为156 N,3根绳索受力加起来为155.2 N,各个关节的受力约等于各个绳索对其产生的拉力。
2.2 机械臂绳索受力分析
通过力矩平衡理论来分析机械臂各关节在不同的旋转角度下绳索所受到的力的大小,以验证仿真结果,并进一步了解机械臂各关节在各状态下绳索的受力状况。单个关节旋转时绳索的分布情况如图11、图12所示。
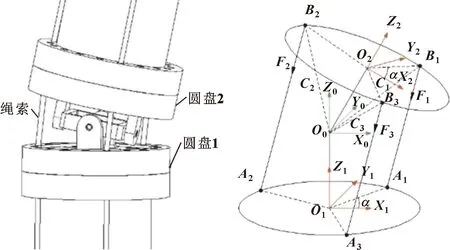
图11 单关节示意 图12 单关节简化图
点受到3根绳索的力以及外力(包括重力负载以及经过此关节的其他绳索)所施加的力矩,对点求矩。首先计算此关节的3根绳索对点的力矩,计算公式如式(1)所示:
=×=[1,1,1]
=×=[2,2,2]
=×=[3,3,3]
(1)
其中:、、分别为3根绳子所受到的力,为矢量;、、分别为3根绳子力的作用点到旋转中心的距离矢量;为各个绳索对关节中心的力矩。

(2)
式中:c为cos;s为sin。
绳子到点的为式(3)—式(5):

(3)

(4)

(5)
式中:为绳子在圆盘中力的作用点到圆盘中心的距离;为绳子力的作用点相对于圆盘坐标系轴的夹角,其中连杆5的为10°,从连杆4到伸缩杆绳索分布的分别为30°、50°、70°、90°、110°,如图13所示。

图13 绳索布线示意
单个关节中每根绳子所受的拉力为

(6)

(7)

(8)
式中:为最终要求的绳索力,为标量,那么最终计算出来的便是一个有方向与大小的矢量。
那么3个绳子对关节在与轴的合力矩为式(9):
=,1+,2+,3
=,1+,2+,3
(9)
关节除了受到3根绳子的力外,还会受到经过该关节的其他绳索对该关节的力矩,以及重力与负载所产生的力矩,计算方法依然为力的作用点去叉乘力对关节的力臂,并把所产生的力矩分解到轴与轴,分别为,e与,e。那么依照力矩平衡原理可以得出公式(10):

(10)
在计算时,先从端部关节往末端关节进行递推计算。由于绳子只能受拉力并不能受到压力,在计算时按照以下方法进行计算:
(1)对于一个关节的3根绳索力,先设置一个绳索力为0;
(2)计算其余2根绳索的受力;
(3)找到受力最小的绳索并设置其大小为0.1 N,使得绳索有一定的预紧力;
(4)计算出其余绳索的受力。
与之前ADAMS瞬态分析得到的绳索力进行比较,结果列于表1、表2。存在误差的原因为ADAMS仿真时绳子要设置质量,所用的铝合金材料与计算时的材料密度、质量等存在一定误差。

表1 关节4绳索受力对比

表2 关节5绳索受力对比
3 机械臂关键部件校核
当机械臂水平时,机械臂根部关节所受的力矩最大,故需校核机械臂水平时根部关节的强度。此机械臂的材料选用高强度铝合金7050-T7451,其屈服强度为470 MPa。
当机械臂水平时,各个关节的角与角为0时,各个绳索受力情况如图14所示。

图14 整个机械臂水平时各绳索受力情况
通过ANSYS Workbench分析伸缩杆关节处的应力状况,根部关节受到的力为前端所有绳索的拉力,又由于计算出伸缩杆处关节在水平方向绳索的总拉力为1 613.24 N,取安全系数为1.8,那么在连杆端面施加3 000 N的力,端面面积为1 071.21 mm,所以需要施加2.8 MPa的压力,之后进行求解,其应力云图如图15所示。

图15 机械臂应力云图
由图15可知:最大应力发生在万向节与中空十字轴的连接处,关节的最大应力约为329 MPa,而7050-T7451铝合金所能承受的最大应力为470 MPa,故所选材料在安全范围内。
4 结论
(1)对超冗余机械臂进行了机械结构改进,在机械臂根部关节加装了可伸缩连杆,使得机械臂具有水平方向移动的自由度,并且在每根连杆的绳索孔内加装了滑轮,减小了绳索与机械臂之间的摩擦,提高了绳索使用寿命。
(2)推导了机械臂的各个关节在任意角度下各绳索受力的计算方法。运用ADAMS对机械臂进行了瞬态分析,并用力矩平衡的计算方法验证了ADAMS的仿真结果。
(3)通过静力学分析得出机械臂受力最大的关节为根部关节,所以对根部关节进行有限元分析,结果表明所设计的机械臂符合强度要求。

