弹体侵彻厚混凝土靶迎弹面成坑效应*

李 明，王可慧，邹慧辉，段 建，古仁红，戴湘晖，杨 慧

（西北核技术研究所，陕西 西安 710024）

关于弹体对混凝土介质侵彻深度的研究较多，基于实验数据，学者们建立了多种经验公式来预测弹体的侵彻深度或弹道极限，为武器设计和混凝土防护结构设计提供了较可靠的方法。但大部分公式仅能预测侵彻能力和贯穿速度，不适用于侵彻过程中迎弹面的成坑效应分析。

Forrestal 等认为弹体侵彻混凝土过程中的靶面成坑深度为弹径的2 倍，宽度为弹径的2～8 倍，形状为近似锥形。薛建锋等对80 g 弹丸侵彻素混凝土的成坑直径和深度进行了实验研究，认为成坑深度是弹径的3～4 倍。钱秉文等研究了克级钨合金弹体超高速撞击混凝土靶的成坑直径和体积随速度的变化规律，认为超高速条件下成坑直径随动能增加单调递增，成坑直径的三次方与弹体动能近似成正比。刘士践等认为高速条件下成坑直径和深度显著高于Forrestal 假设。邓国强等认为弹丸冲击作用下混凝土的破坏形态与弹速、靶厚及混凝土强度密切相关。吴祥云等通过不同缩比率下的低速侵彻实验拟合了成坑深度和成坑直径的经验公式。张爽等对比了现有成坑模型与文献数据，通过数据拟合建立了考虑弹体质量和初速度影响的刚性弹撞击素混凝土成坑深度经验公式。可见，弹体质量、初速度和靶板强度以及钢筋等对迎弹面成坑均有一定影响。

目前，关于弹体侵彻混凝土成坑效应的研究较少，对成坑效应的分析多集中在成坑深度，对成坑直径和成坑角的分析相对匮乏。本文中，基于大量实验数据，建立适用于大着速范围的混凝土迎弹面成坑参数计算模型，分析影响成坑效应的参数，并讨论不同条件下迎弹面成坑耗能，以期为侵彻弹体设计和工程防护提供参考。

1 成坑效应计算

1.1 成坑现象

弹体侵彻混凝土靶时迎弹面典型成坑形态如图1 所示。靶面在弹着点周围发生剥落，并形成漏斗状的弹坑，在弹坑附近往往还会出现少量裂纹。当靶板为钢筋混凝土靶时，受表层钢筋的影响，靶面形成浅碟形漏斗坑，裂纹数量较素混凝土靶也减少，如图2 所示。

图1 混凝土靶成坑形态[6]Fig. 1 Typical crater of concrete target[6]

图2 钢筋混凝土靶成坑形态[15]Fig. 2 Typical crater of reinforced concrete target[15]

弹体在靶板中形成的破坏区一般可分为漏斗形坑和直弹道区，如图3 所示。漏斗坑的完整成坑效应包括不同侵彻深度处弹坑横向尺寸的全部信息。混凝土抗拉强度低、脆性显著且存在内部缺陷，因此混凝土介质中的成坑一般难以用简单形状函数描述。其典型特征是在中央坑周围存在一个边缘不规则的剥裂区域，近似为漏斗锥形，内壁凹凸不平，由于侵彻条件具有轴对称性，因此该剥落区域在靶表面近似呈圆形。在简化分析中，采用成坑直径、成坑深度、成坑角θ 等特征尺寸来描述漏斗坑几何信息。

图3 成坑区Fig. 3 Crater zone

1.2 成坑深度

在侵彻成坑效应分析中，学者们对成坑深度尤为关注，并根据实验数据总结了一些经验公式。通常可采用无量纲参数来描述成坑深度：

式中：为弹体直径，单位m。

对于素混凝土靶，Forrestal 等认为=2。晋小超认为刚性弹侵彻混凝土成坑深度与头部长度和弹体直径相关，与速度、靶板强度、质量等无关。温志鹏等认为成坑深度和直径在低速下随初速度提高而增大，但在超高速条件下随初速度提高而减小；成坑深度与弹丸直径成比例关系，靶体的机械性能越高，比例系数越小。

张爽等根据文献实验数据（弹体质量为0.003 2～25 kg、撞击速度为150～1 700 m/s、直径不大于100 mm），拟合了考虑质量和速度的公式：

钱秉文等利用Holsapple-Housen 模型得到了钨合金短杆弹超高速侵彻混凝土成坑效应中成坑深度的表达式：

式中：为拟合参数，ρ为弹体密度，为靶板抗压强度。

此外，吴祥云等通过分析侵彻实验数据，认为成坑深度与靶材强度、速度和缩比率等相关，根据200～450 m/s 速度下的侵彻数据，拟合得到：

式中：为与混凝土靶材性质相关的因子，为与弹速相关的因子，为缩尺效应因子。

闪雨对600～1 500 m/s 速度范围的实验数据进行了线性拟合，得到：

钢筋混凝土中的钢筋对混凝土开裂有一定的抑制作用，能够减小混凝土表面的剥落面积和裂缝宽度。Dancygier 等进行了钢筋混凝土靶侵彻实验，并分析了卵石类型和尺寸、钢筋直径和排布以及混凝土基体强度对侵彻结果的影响，认为钢筋主要通过限制破坏区域面积来提高靶板的抗侵彻能力，配筋率对弹体贯穿阻力影响较小。对于钢筋混凝土靶迎弹面成坑深度，周宁等取Forrestal 等提出的2 倍弹径。陈小伟指出钢筋混凝土靶侵彻弹坑的形状和深度取决于钢筋网眼的布局和埋嵌，但并未给出取值范围。

上述不同的经验公式各有特色，并且具有不同的适用范围。图4 中给出了成坑深度经验公式与实验数据对比。可以看出，Forrestal 公式和晋小超给出的拟合公式没有考虑速度的影响，因而只适用于低速情况；吴祥云等和温志鹏等采用同一组低速实验数据进行拟合，得出的公式同样不适用于高速情况；闪雨给出的公式适用于低速和超高速情况，但在中高速条件下误差较大。

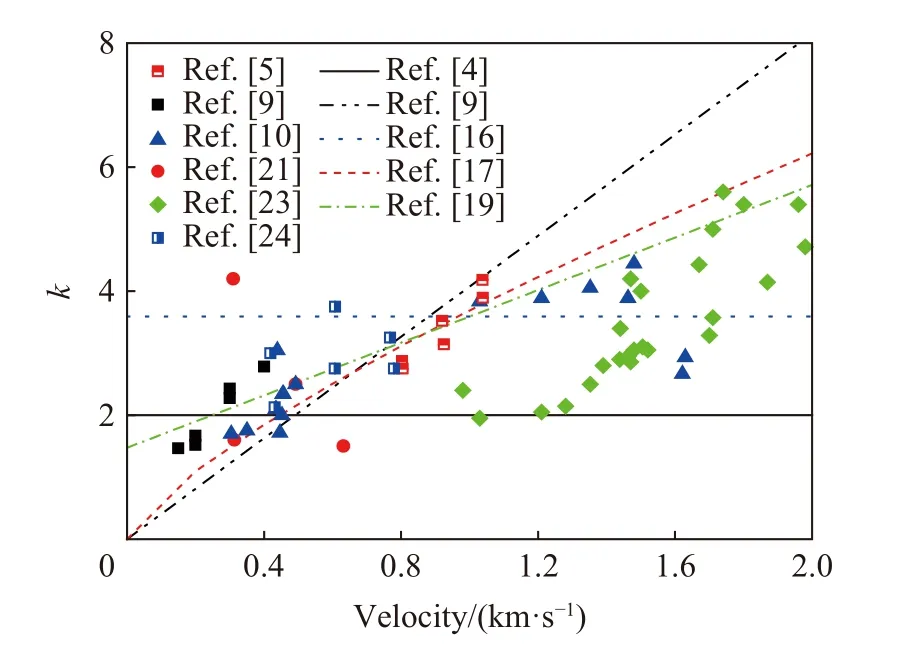
图4 成坑深度经验公式与实验值对比Fig. 4 Comparison of the empirical formula result with the experimental data of crater depth

进一步分析实验数据可知：成坑深度与撞击速度、靶板强度、名义配筋率以及弹体直径、质量等因素相关。只考虑单一因素得到的公式适用范围较窄。成坑深度与各主要影响因素的关系可表示为：

式中：、、α、β、γ 为拟合常数；为靶板强度，单位Pa。名义配筋率与靶板的配筋率以及首层钢筋相对位置有关：

式中：为配筋位置系数。根据实验数据，参考张爽等的分析，认为首层钢筋越靠近靶表面对成坑抑制越明显，当首层钢筋深度大于素混凝土计算坑深后，影响可忽略，采用Dose Resp 函数表达：

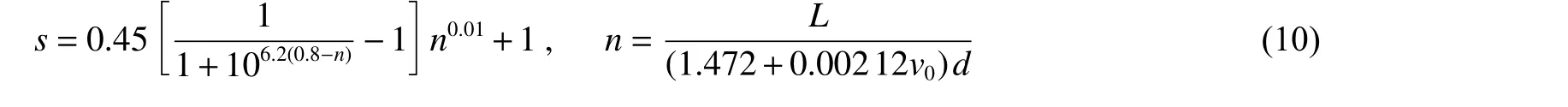
式中：为首层钢筋埋深。

基于开展的大量不同质量、速度、靶板强度条件下的混凝土侵彻实验数据和文献[5-6, 9, 21, 23]的数据，见表1。拟合得到考虑撞击速度、靶板强度/配筋，以及弹体直径/质量等因素的成坑深度计算公式：

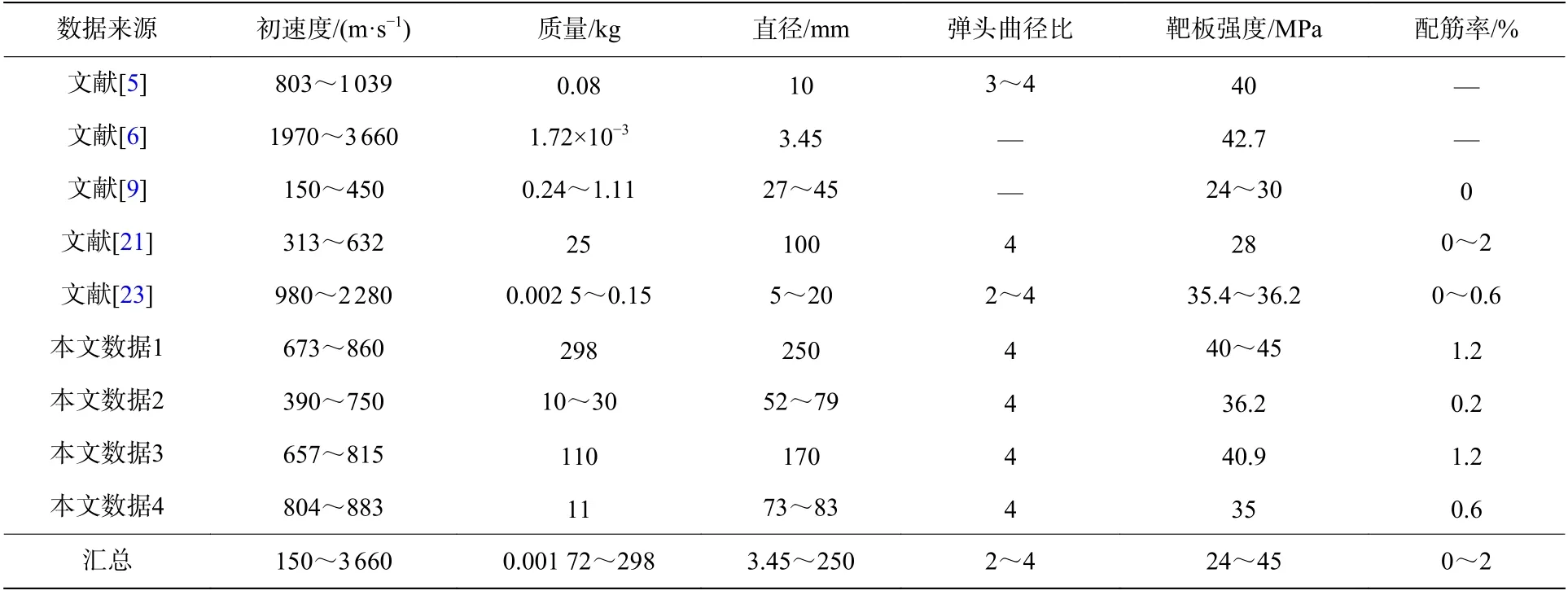
表1 本文中参考的实验数据Table 1 Experimental data referred to in this paper

采用本文中建立的成坑深度计算公式（式(11)）对实验数据进行验证，误差分布及趋势如图5 所示。吴祥云等、闪雨提出的经验公式误差较大，且不适用于高速情况。总体来看，大部分经验公式误差均较大：一方面，由于成坑效应的影响因素多，且实验数据本身存在一定的离散性；另一方面，由于部分经验公式的提出条件仅限于较窄的速度范围，当速度超出该范围时，由于成坑机理的变化，误差显著增大。而式(11)的误差较小，与实验数据吻合较好。

图5 成坑深度公式预估偏差对比Fig. 5 Predictive deviations by crater depth formulas

1.3 成坑直径

关于成坑直径的分析讨论较少，引入无量纲参数来描述成坑宽度，即=/。Forrestal 等认为，靶面成坑宽度为弹径的2～8 倍。吴祥云等认为与靶材强度、速度和缩比率等相关。Donald认为速度较高时，动能成为影响成坑直径的主要因素。Takagi 等认为成坑直径与弹径的0.45 次方成正比。图6 为吴祥云等给出的成坑直径经验公式与实验数据的对比。弹体的相对成坑直径随撞击速度提高而增大。吴祥云公式在低速段与实验数据拟合较好，但过高估计了高速条件下的成坑直径。

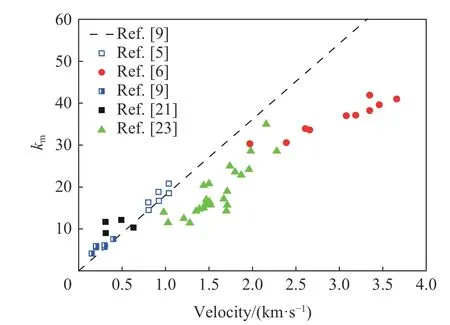
图6 成坑直径经验公式与实验值对比Fig. 6 Comparison of the empirical formula results and the experimental data of crater diameter

分析表1 所列实验数据，发现成坑直径与成坑深度规律一致，采用与成坑深度相同的形式来拟合成坑直径公式，可得：

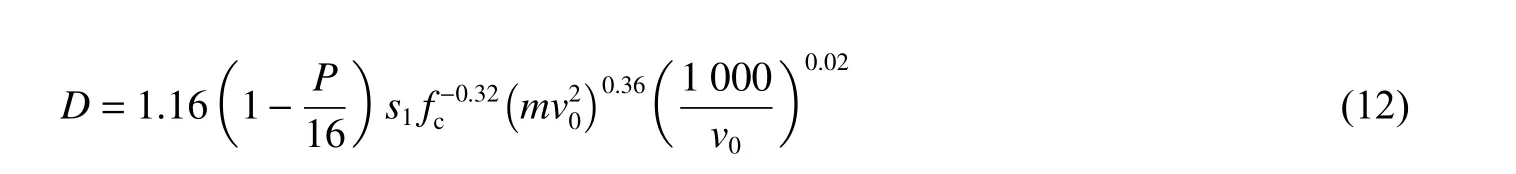
图7 给出了不同经验公式对成坑直径的计算误差分布及趋势。从图7 可以看出，本文中给出的成坑直径与实验数据吻合较好，且适用于较宽的速度范围。

图7 成坑直径公式预估偏差对比Fig. 7 Comparison of predictive deviations of crater diameter formulas

1.4 成坑角

根据图3 中成坑区尺寸的几何关系，可以得到：

联合式(11)～(13)，可推导出成坑角计算公式：

根据式(14)可知，侵彻速度越高、弹体质量越大，成坑角越小；对于岩石类材料，弹体质量从百克级到百千克级、速度为400～3 000 m/s，成坑角在15°～17°之间，与Donald给出的结果一致。文献[9]中给出的成坑直径与成坑深度比为3.75，即成坑角约28°，认为成坑直径和深度与靶板强度有关，但成坑角与其无关，这主要是由于其所参考的实验数据范围较小造成的。

图8 给出了不同条件下迎弹面成坑角及其随初速度的变化趋势。从图8 可以看出，本文中公式预测得到的成坑角与实验数据吻合较好。

图8 公式预测值与成坑角实验值[5-6,9,21,23]对比Fig. 8 Comparison of the empirical formula results and the experimental data[5-6,9,21,23] of crater angle

2 成坑效应讨论

2.1 成坑效应的影响因素

采用式(11)～(12)和(14)对10 kg 弹体侵彻钢筋混凝土靶的成坑效应进行分析，钢筋混凝土靶的配筋率为1%。

图9 为不同条件下相对成坑深度随撞击速度的变化关系。对比分析可知：(1)随靶板强度或配筋率增加而减小，随弹体质量增加而增加，基本不受缩比率影响；(2) 由于配筋的存在，并不随速度的提升而线性增加，而是在某一速度处达到峰值后，先减小，随后再增大；(3) 首层配筋埋深增加会延后峰值对应的速度。这是由于在撞击速度较低时，成坑深度小于首层钢筋的埋深，随速度的提升而增大；当撞击速度提高到使钢筋对混凝土的破坏起到约束作用时，使得成坑深度下降；当撞击速度继续提高时，钢筋的约束作用不占主导地位，因此成坑深度继续随速度的提高而增大。

图9 不同因素对成坑深度的影响分析Fig. 9 Influence of different factors on crater depth

图10 对比了弹体撞击混凝土成坑角与初速度及质量的关系。可以看出：(1) 弹体质量越大，成坑角越小，但质量对成坑角影响不大，从千克级到吨级，成坑角变化小于5°；(2) 初速度越高，成坑角越小，初速度从300 m/s 提高到3 000 m/s，成坑角减小约12°；(3) 在常见侵彻速度和质量范围内，成坑角为15°～24°。

图10 成坑角与撞击速度及质量的关系Fig. 10 Relation of the crater angle with impact velocity and mass

2.2 迎弹面成坑耗能

弹体侵彻混凝土时，弹靶接触截面处的冲击压力远大于靶体材料的强度，形成远大于弹体口径的弹坑，混凝土迎弹面成坑特性反映了打击过程中能量分配份额。研究表明，侵彻成坑阶段的弹体过载与时间成线性关系，且在成坑结束后达到峰值，侵彻过载峰值为平均过载的2 倍，因此：

弹体侵彻深度采用Young 方程计算：

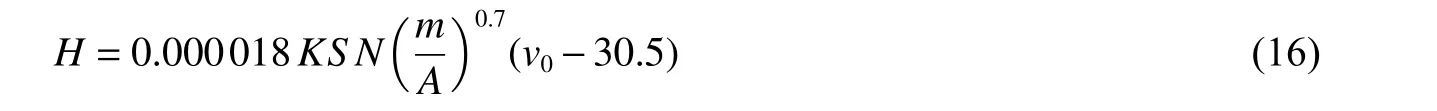
式中：为质量修正因子；为混凝土的可侵彻系数，与靶板的配筋率、养护时间、厚度和强度等相关；为头形影响系数；为弹体横截面积。

根据撞击速度、成坑深度和过载峰值推算成坑结束时的弹体速度为：

因此，成坑阶段消耗的弹体动能比例为：

可见成坑阶段耗能只与弹体的侵彻能力和成坑深度有关。图11 为不同条件下弹体侵彻成坑耗能比例。分析发现：(1) 成坑耗能比例随速度提高而减小，常见弹靶条件下迎弹面成坑耗能占总动能的10%～25%；(2) 弹体质量越大，成坑耗能比例越小，因此进行缩比实验时弹体会用更大比例的能量来成坑，缩比率不宜过大；(3) 配筋率和靶板强度变化对成坑耗能影响较小；(4) 弹头曲径比（caliber radius head，CRH）变小会增加侵彻阻力，提高弹体过载，成坑耗能相应增加。

图11 不同条件下的成坑耗能比例Fig. 11 Energy consumption ratio under different conditions

柴传国等开展了1.4 kg 弹丸侵彻混凝土实验，并采用高速录像手段详细测量了弹体成坑过程，给出了成坑速度和能量变化等参量。采用式(18)对该实验工况进行了计算，结果见表2。表中：、分别为成坑结束时弹体速度的实验值与估算值，δ、δ分别为成坑耗能的实验值与估算值。可知估算值与实验数据吻合较好。

表2 成坑耗能计算结果与实验结果[24]的对比Table 2 Comparison of the calculated energy ratios with the experimental results[24]

式(17)～(18)可用的前提是侵彻深度可用Young 方程计算，因此只适用于速度低于1 400 m/s且弹体结构基本完整的情况，不适用于超高速侵彻。显然，速度足够高时弹体会部分或完全破坏，甚至不会产生弹洞，这种情况下弹体的动能全部用来成坑。

3 结 论

基于300～3 700 m/s 速度下弹体侵彻厚混凝土靶实验数据，考虑撞击速度、靶板强度、配筋以及弹体直径和质量等因素，建立了新型成坑效应计算公式，对成坑深度、直径和角度的计算结果与实验结果吻合较好。

分析了成坑效应影响因素，结果表明，无量纲成坑深度受靶板强度、配筋率和弹体质量的影响较大，而受缩比率的影响较小；对于钢筋混凝土，成坑深度随撞击速度提升呈先增大后减小再增大的变化规律。在常见的侵彻速度和弹体质量范围内，成坑角为15°～24°。弹体质量对成坑角影响不大，从千克级到吨级，成坑角变化小于5°；随着初速度提升，成坑角减小，初速度从300 m/s 提升到3 000 m/s，成坑角减小约12°。

建立了成坑阶段耗能计算公式，计算结果与实验数据吻合较好。基于公式分析表明，常见弹靶条件下迎弹面成坑耗能占弹体总动能的10%～25%，且配筋率和靶板强度对成坑耗能比例的影响较小；弹体质量越小，成坑阶段耗能占比越大，缩比实验时弹体会用更大比例的动能成坑，因此缩比率不宜过大。