下穿铁路隧道爆破振动衰减规律研究*

单仁亮，赵 岩，王海龙,，董 捷，仝 潇，李兆龙，王东升

（1. 中国矿业大学(北京)力学与建筑工程学院，北京 100083；2. 河北建筑工程学院河北省土木工程诊断、改造与抗灾重点实验室，河北 张家口 075000）

随着交通基础设施建设的迅猛发展，地下空间利用率显著增长，因建筑物分布密集，公路、铁路隧道不可避免地会穿越村庄、城镇及既有干线等。钻孔爆破作为山岭隧道破岩掘进的主要方式，诱发的爆破振动会对周边构筑物产生不利影响。因此，研究岩石诱发的爆破振动衰减规律对周边构筑物的使用安全性，具有重要意义。

目前，研究大多以爆破峰值振动速度为指标、结合振动频率及持续作用时间进行评价，并通过现场实测及数值模拟的方式对爆破振动响应特征展开研究。Yu 等利用相似模拟实验，研究节理弱面对爆破振动传递的影响：随着爆破振动传播路径上节理数量的增多，爆破地质参数及衰减参数α 均呈增大的趋势；此外，节理弱面的存在会增加爆破振动能量中高频部分的比重。朱正国等深入研究总装药量对爆破振动强度的影响，结果证实爆破振动强度与装药量及比例距离之间存在某种线性关系。Qin 等发现三台阶预留核心土开挖方法可以有效控制既有地铁隧道的爆破振动，并通过ANSYS/LS-DYNA 软件对实测结果进行了数值模拟验证。Jiang 等依托地铁隧道下穿工程，研究地铁爆破振动对既有燃气管道的影响，通过量纲分析得到反映管道正上方地面振动速度的物理方程，基于第四强度准则计算了不同管道运行压力作用下运输管道的振动速度安全阈值。Lu 等通过现场实测及数值分析的方法，研究了临空自由面数量对爆破振动衰减规律的影响：1 个自由面的爆破振动速度远大于2 个或3 个自由面的爆破振动速度，由数值计算得知，1 个自由面的最大单响药量与2 个自由面的最大单响药量的比小于0.79 时，爆破振动效果相近。刘彦涛则利用最小二乘拟合及数值模拟，对隧道爆破振动信号特征进行研究，详细划分了爆破振动的影响区域。

综上所述，对爆破振动效应的研究大多通过现场实测或数值模拟的方式进行，但针对爆破振动效应的理论分析很少见。爆破振动效应的理论研究对探讨爆炸应力波的传播规律，有效控制爆破损伤均具有重要的意义。本文中，首先，依托下穿隧道爆破工程实例，基于Heelan 短柱药包理论的波动方程解析解，推导适用于隧道爆破振动速度的衰减模型方程；然后，通过量纲分析对其进行验证；最后，分别讨论爆破振动拟合方程的两种药量表达形式，对比不同拟合方法的预测效果。

1 理论分析

爆破施工过程中，爆破振动能量以应力波的形式向外界传播。受爆源特征、围岩力学性质、地形地质条件等影响，不同工程条件下的爆破振动衰减规律存在差异，从应力波传递的角度出发研究爆破振动速度的演化规律是可行的。

由文献[14]可知：目前，通常通过萨道夫斯基公式和USBM 模型，拟合爆破峰值振动速度；同时，也采用印度标准协会标准、Langefors 等经典方法预测爆破振动速度。

表1 为常用爆破峰值振动速度经验公式。表中，为爆破峰值振动速度（cm·s），为爆心距（m），为最大单响药量（kg），、、β、α 为相关拟合参数。

表1 爆破峰值振动速度的经验公式[14]Table 1 Prediction formulas of blasting peak vibration velocity[14]

以上经验公式中，均只考虑了爆心距和装药量，并未反映装药半径、钻孔半径、炮眼布置方式及岩体力学性质等对振动速度的影响。为此，基于短柱药包激发的波动解析解，本文中主要研究远场爆破振动强度的衰减规律，并通过量纲分析进行验证。

1.1 爆破振动衰减

当爆心距大于柱状药包的长度及应力波波长时，可以将柱状装药简化为短柱药包的瞬时起爆。基于此，Heelan 等通过理论推导得到短柱空腔在瞬时内部荷载激励下远场低频波动的解析解。

如图1 所示，设内部瞬时激励荷载()作用在长d、半径的短圆柱空腔内壁，则位移场为：

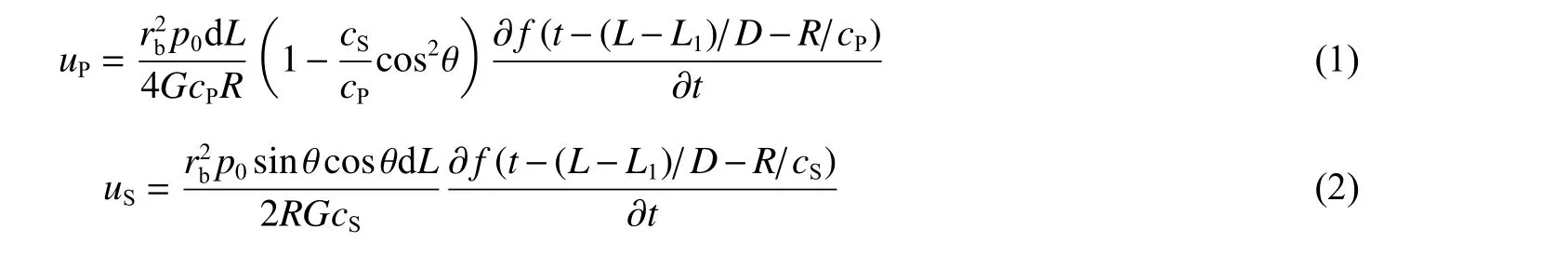
式中：为由压缩波（P 波）引起的位移，为由剪切波（S 波）引起的位移，为炮孔初始爆轰压力，()为与激励荷载相关的时间函数，为作用时间，为岩石的剪切模量，、分别为P 波、S 波的传播速度，为爆轰波的传播速度，为爆心距，、分别为的计算上下限，[0,]为瞬时荷载作用位置坐标。

由图1，短柱药包爆炸激发的径向位移u、竖向位移u分别为：

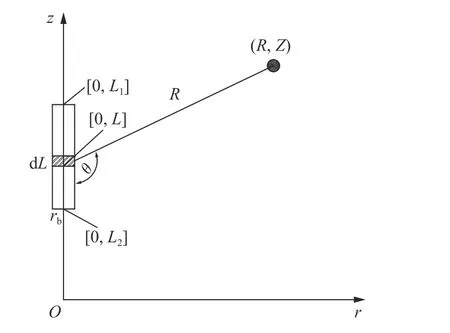
图1 短柱瞬时荷载作用Fig. 1 The instantaneous load action of a short column

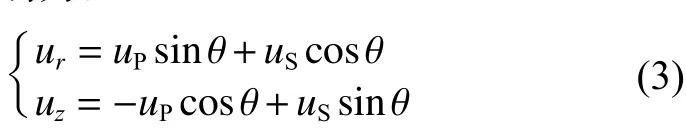
那么，瞬时荷载激发的径向速度v、竖向速度v分别为：

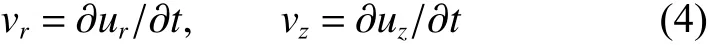
由文献[19-20]，S 波为爆破近区的主导波，而P 波在爆破近区及爆破远区均为其重要组成部分。本文中，因主要考虑远区的爆破振动传播规律，仅计算由P 波诱发的爆破峰值振动速度：

式中：为计算待定系数。

实际岩体具有黏弹性，且具有一定的阻尼性质，则岩体的爆破振动衰减方程修正为：

式中：、α 为计算待定系数。炮孔壁上振动峰值速度为：

则式(8)可简化为：

式中：为与场地条件有关的系数，λ 为衰减系数。

1.2 改进拟合公式

由文献[21]，式(10)适用于单孔爆破。隧道爆破工程中，往往采用多孔多段起爆，单孔爆破较少见。为此，本文中试图寻求一种适用于隧道爆破的等效解决方法。

1.2.1 等效作用边界

根据应力状态的差异，爆源附近的岩体可划分为粉碎区、破碎区和弹性振动区。实际爆破振动测试往往位于弹性振动区，位于这个区域的岩体可以近似为弹性体，而位于粉碎区和破碎区中的岩体受爆炸应力波破坏严重，不能简单视为弹性体，可以将非弹性区外边界视为爆破荷载等效作用边界。

柱状装药条件下，粉碎区半径和破碎区半径分别为：

式中：σ、σ分别为岩石的动单轴抗压强度、动单轴抗拉强度，σ为多向应力条件下的岩体动抗压强度，为炮孔初始爆轰压力，β 为传播衰减系数，β=(2-)/(1-)，为岩石的泊松比。通常，粉碎区半径为装药半径的3～5 倍，破碎区半径为装药半径的10～15 倍。

不考虑炮孔之间的相互作用时，每个掏槽孔起爆可近似看作一个短圆柱空腔在半无限介质中受内部瞬态荷载的作用，将掏槽段起爆的等效作用边界近似为多孔爆破破碎区的包络线是可行的。辅助孔、崩落孔、周边孔及底板孔等非掏槽孔则通过贯通相邻炮孔的轴线来破坏抛掷岩石，可以将其形成的临空面近似为等效作用边界。这里，定义为等效作用边界半径。图2 为掏槽孔爆破的等效作用边界示意图。

图2 掏槽孔等效作用边界Fig. 2 The equivalent boundary of cutting hole blasting

1.2.2 等效荷载

根据凝聚装药爆轰波CJ 理论，耦合装药时，炮孔壁上的初始爆轰压力为：

当不耦合系数较小时，炮孔壁上的初始爆轰压力为：

式中：ρ为炸药密度，γ 为炸药的等熵系数，、分别柱状药卷、炮孔的直径，υ 为爆生气体的等熵系数，为爆生气体的临界压力，取为200 MPa。

单个炮孔对应的等效爆破荷载随爆心距的变化为：

式中：为掏槽段炮孔的个数。

那么，掏槽段对应的等效爆破荷载为：

而对辅助孔、周边孔等非掏槽孔（见图3），可将爆破荷载等效作用在炮孔中心线与炮孔轴线所在的平面上，等效荷载为：

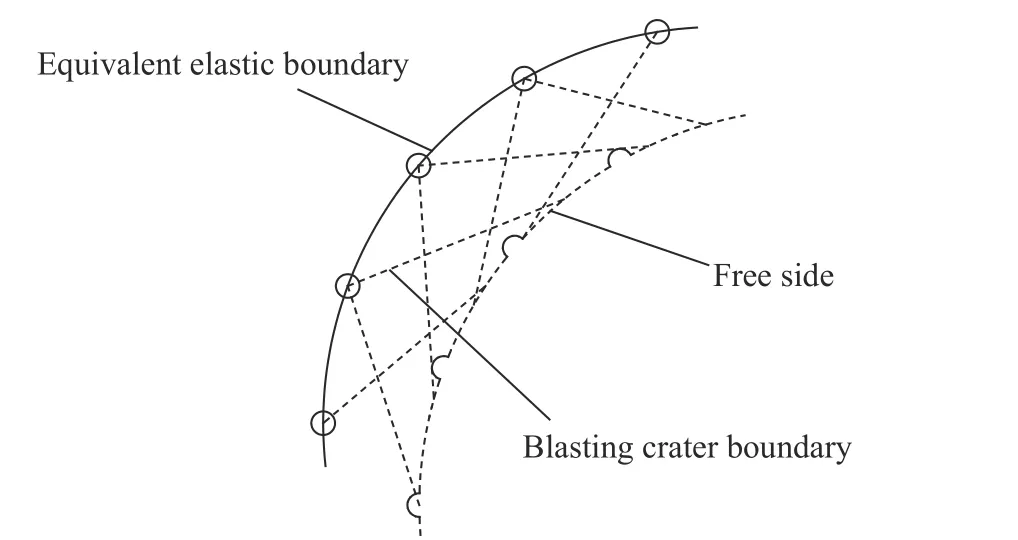
图3 等效边界[23]Fig. 3 The equivalent elastic boundary[23]

式中：为相邻炮孔的距离。

与经验公式相比，引入等效作用边半径和等效作用荷载替代和，可体现炸药特性、装药半径及炮孔布置等条件，更贴近工程实际。

综上所述，改进的爆破峰值振动速度衰减方程为：

1.3 量纲分析

为了验证式(21) 的可行性，且不失一般性，利用量纲分析，推导隧道爆破峰值振动速度的衰减方程。

选择岩体密度ρ、纵波传播速度、爆心距、岩体弹性模量、等效作用半径作为影响爆破振动速度的主要影响因素，并选取、、ρ 作为独立量纲进行量纲分析：

式中：为待定参数。可见，式(26)与式(21)具有相同的形式，验证了改进公式的可行性。

2 工 程

2.1 工程背景

以崇礼铁路工程中隧道爆破工程为例。隧道起止里程分别为DK62+310、DK67+800，全长5 490 m，洞身大段、山势陡峭，地貌单元属于中低山区，整体地形呈中间高、两侧低，地势起伏较大。地质勘探显示，隧道地层岩性主要为第四系全新统人工填土，第四系上更新统坡洪积层新黄土、砾石土、卵石土及碎石土。主要岩性有粗面岩、流纹岩、凝灰质砾岩、粗面安山岩和斜长片麻岩等。隧道主洞部分区域下穿既有村庄，下穿区域内隧道围岩设计为Ⅲ级，图4 为下穿隧道平面地形图。

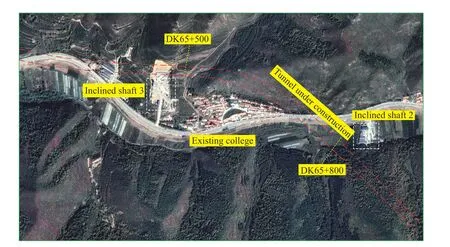
图4 下穿隧道平面地形图Fig. 4 Topographic map of the underpass section of the tunnel

2.2 施工方案

根据隧道的围岩等级、地质条件，采用全断面法爆破掘进，控制循环进尺为2.8～3.6 m。围岩密度为2 630 kg/m，纵波波速约为4 500 m/s，爆轰波波速约为3 600 m/s。爆破施工采用2#岩石乳化炸药，炸药密度为1 g/cm，药卷直径为32 mm，炮孔直径为40 mm。根据循环进尺确定炮孔深度，取范围为3.5～4.5 m。掏槽孔单孔装药为2.7 kg，辅助孔单孔装药为1.5～2.4 kg，底板孔单孔装药为2.1 kg，周边孔单孔装药为1.2 kg，在施工中动态调整，确定合理的装药量。采用电子数码雷管起爆，它可以精准控制各段炮孔的起爆时间，本文中利用数码雷管将各段雷管的起爆微差时间间隔控制为50 ms。隧道爆破采用柱状不耦合装药，填塞长度不小于0.3 m。具体装药量情况见表2。图5 为隧道断面炮孔布置。

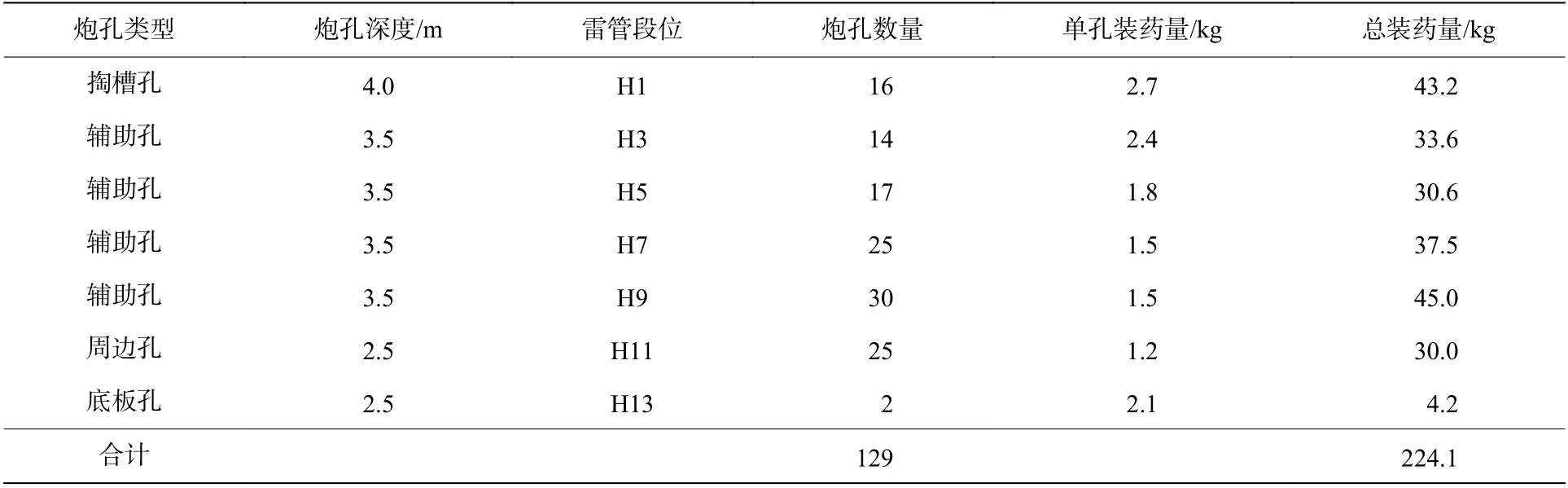
表2 隧道爆破装药情况Table 2 Charges for tunnel blasting

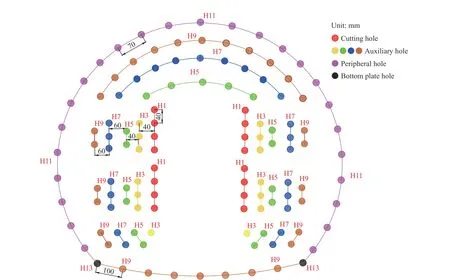
图5 隧道炮孔布置Fig. 5 The layout of the tunnel blast holes

2.3 监测方案

在村庄内部选择合适测点，布置爆破测振仪，组建光纤通讯系统，完成自动化爆破振动监测。爆破振动监测采用中科测控公司的TC-4850N 测振仪，配套三轴向振动速度传感器TCS-B3，可同时采集、和方向的爆破振动速度，并通过系统软件实时上传、处理数据。具体测点布置见图6。

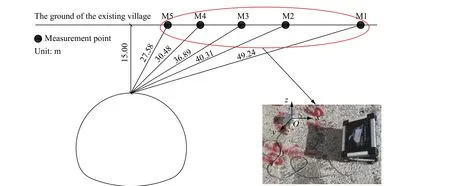
图6 爆破振动测点布置Fig. 6 Layout of the blasting vibration measurement points

3 数据的分析和拟合

3.1 数据分析

2020 年10 月31 日至12 月2 日，进行了多次爆破振动现场监测，典型爆破振动波形如图7 所示。这里，选取具有代表性的监测结果进行研究，监测结果见表3。

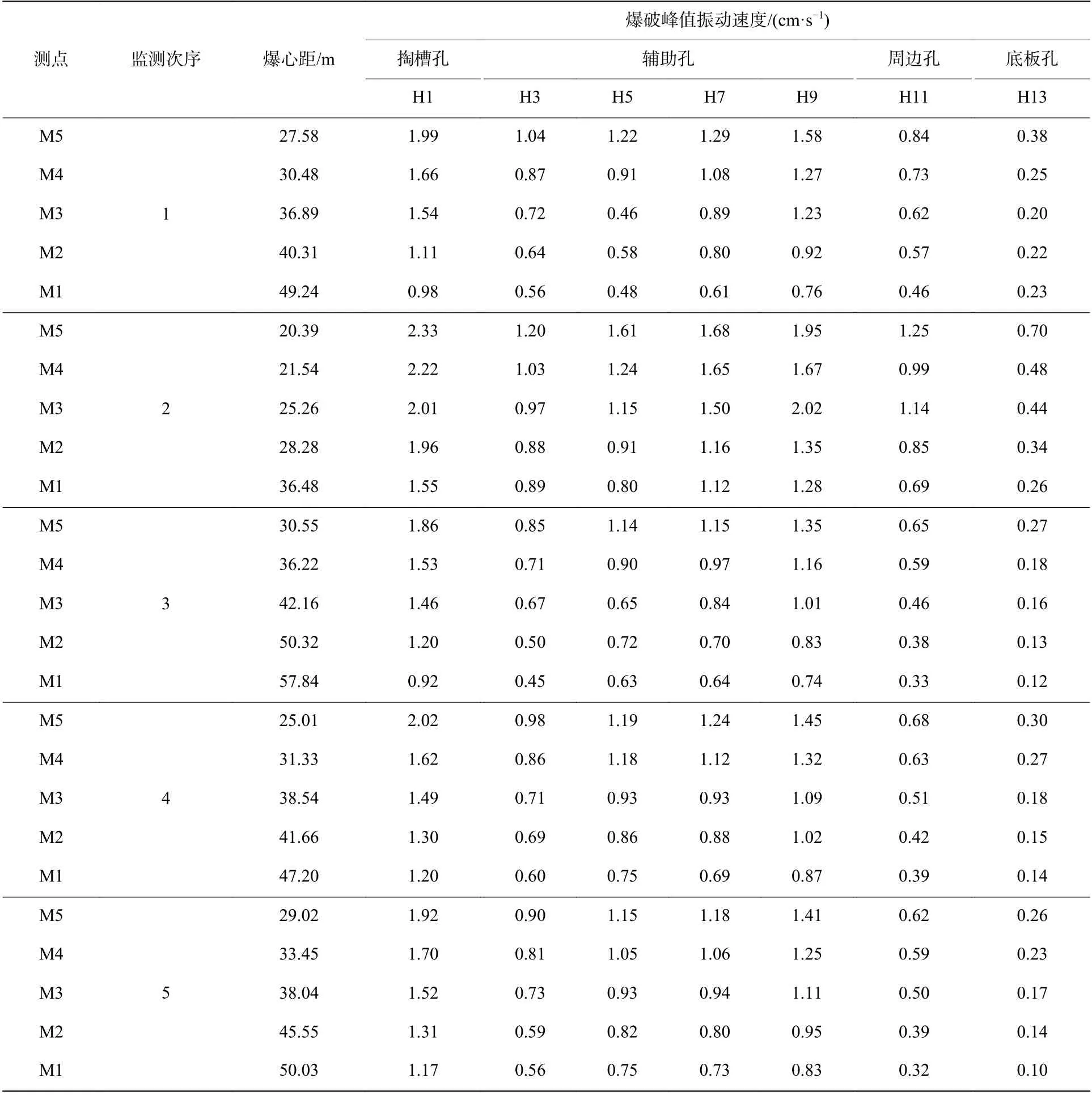
表3 爆破峰值振动速度及相关参数Table 3 Blasting peak vibration velocity and related parameters

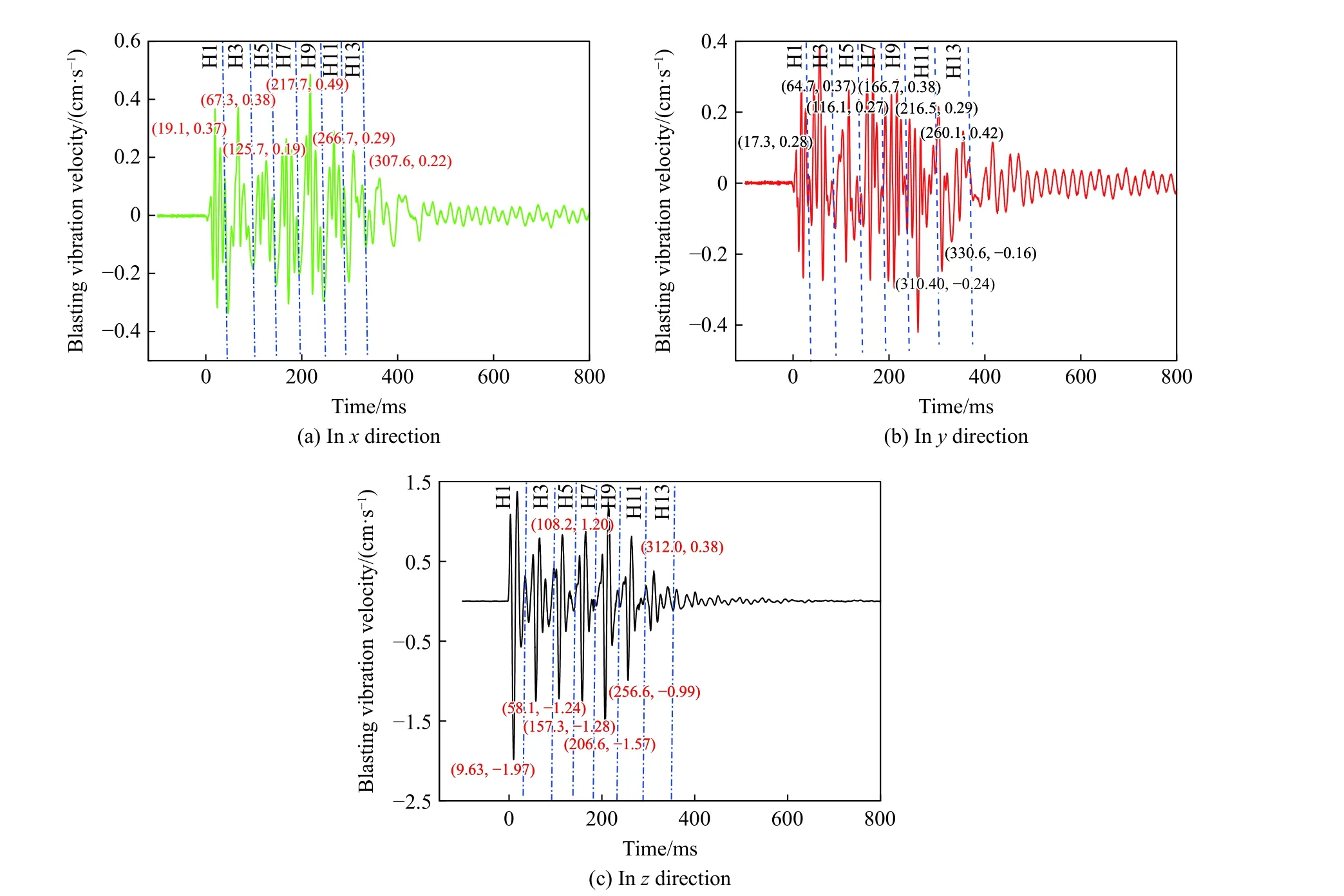
图7 典型的爆破振动速度波形Fig. 7 Typical blasting vibration velocity waveforms

按照GB 6722-2014《爆破安全规程》，应选取振动速度最大的进行研究。而在本文中，爆破振动速度以方向最大，这里只对方向的爆破峰值振动速度进行分析。采用电子数码雷管控制相邻段位的时间间隔均为50 ms，而由图7 可以看出，相邻雷管段位对应的振动速度的时间间隔也约为50 ms。在方向，段位1～13 雷管对应的时间分别为9.63、58.1、108.2、157.3、206.6、256.6 和312.0 ms，相邻段位的时间间隔分别为48.47、50.1、49.1、49.3、50.0 和55.4 ms，均分布在50 ms 左右。由以上分析可知，采用电子数码雷管起爆并未发生相邻雷管段位波形叠加的现象，这有利于减小爆破振动对周边环境的影响。掏槽孔爆破只存在一个临空面，爆破振动效应较大，而掏槽段对应的振动速度并不一定最大，由图7 可以看出，、方向的最大振动速度分别由段位9、11 雷管起爆引起。

每个雷管段位对应的爆破峰值振动速度均随着爆心距的距离增大而减小，且衰减速率随爆心距增大也呈减小趋势。段位1 掏槽孔或段位9 辅助孔或段位11 周边孔对应的振动速度最大，这与炮眼布置情况、单孔装药量、爆心距及起爆顺序等有关。隧道爆破开挖过程中，掏槽孔、辅助孔、周边孔及底板眼在装药条件、炮眼布置情况、临空面条件等都存在较大差异，这导致不同类型炮孔诱发的爆破振动存在差异。

为了提高炮孔利用率，隧道爆破中广泛使用空气柱间隔不耦合装药。实际应用中，根据式(14)～(19)，以不耦合系数为分类依据，可分别得到不同装药结构对应的等效爆破荷载，并将代入且改进获得式(21)，可以反映不同柱状装药结构对爆破振动衰减规律的影响。刘达等指出，等效作用半径的选取与隧道或隧洞的断面形式及炮孔布置方式有关：当断面为圆形、炮孔布置大致规则逐圈爆破时，各段同时起爆的炮眼形成的非弹性区包络线近似为闭合环形；当断面为圆拱直墙型、某些炮孔连接线为矩形一条边不能形成闭合的圆形时，将会影响峰值振速的拟合效果。如图4 所示，下穿隧道断面近似为圆形，且均大致按逐圈布置炮孔，因此式(21)理论上适用于本隧道爆破工程。按照临空面数可将隧道爆破炮孔划分为两大类：掏槽孔起爆时只有前方掌子面一个自由面；而辅助孔、周边孔及底板眼起爆时，除掌子面以外，掏槽爆破也可为他们增加一个临空面，这有助于爆破振动波的传递及衰减。为了体现自由面对爆破振动拟合的影响，对于掏槽孔及非掏槽孔，在等效爆破荷载的计算过程中有区别（见式(19)～(20)），对辅助孔、周边孔等非掏槽孔，将爆破荷载等效作用在炮孔中心线与炮孔轴线所在的平面上，荷载大小可根据力矩平衡原理计算得到。此外，等效作用半径的选取也应考虑临空面数的影响：对掏槽孔起爆，根据式(11)～(12)可得到粉碎区及破碎区半径：对辅助孔、周边孔等非掏槽孔，则可取各圈孔的圈径替代等效半径进行计算。综上所述，为准确反映隧道爆破振动的衰减规律，应依据不同雷管段位及不同炮孔类型分类进行研究。

3.2 改进公式的拟合

以下拟合式中，距离、药量和速度的单位均分别为m、kg 和cm/s。

由实测数据（见表3），利用最小二乘法回归分析，拟合结果见表4，拟合线如图8 所示。由表4 可知，不同段位雷管诱发的峰值振动速度采用式(21)的拟合效果良好，相关系数均大于0.8，证明改进公式可以反映下穿隧道施工诱发爆破振动衰减的规律。

表4 爆破峰值振动速度采用式(21)的拟合效果Table 4 Fitting effects of equation (21) for the blasting peak vibration velocity

由图8 可知，相同类型炮孔对应的峰值振动速度基本可以由相同方程表示，如段位3、5、7、9 雷管组成的辅助孔对应的爆破峰值振动速度与等效作用半径及爆心距有良好的拟合关系，相关系数为0.875。这说明，将相同类型炮孔诱发的振动速度统一进行拟合分析是可行的，这样不仅可以节省运算时间，而且可得到更符合工程的爆破振动衰减规律。综上所述，引入等效作用半径作为拟合变量，不仅可准确预测不同段位雷管对应的爆破峰值振速，而且适用于不同类型炮孔对应的爆破振动速度的拟合分析。

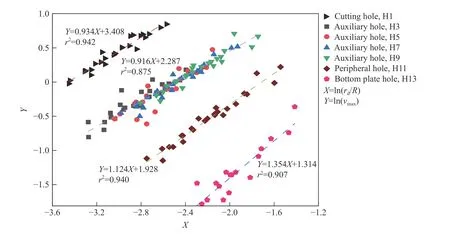
图8 爆破峰值振动速度采用式(21)的拟合曲线Fig. 8 Fitting curves of equation (21) for the blasting peak vibration velocity

3.3 几种拟合公式的比较

为了验证本文中改进拟合方程的可行性和普适性，通过常见的球形装药和柱状装药表达式展开对比分析。

对球形装药一次爆破，装药量与等效作用半径的关系为：

采用式(28)～(29)，对两次爆破振动实验数据进行回归分析，对比式(21)与式(28)～(29)的拟合效果。拟合结果的对比见表5，拟合线如图9～10 所示。

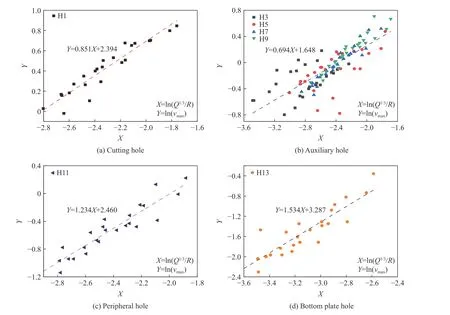
图9 爆破峰值振动速度采用式(28)的拟合曲线Fig. 9 Fitting curves of equation (28) for the blasting peak vibration velocity

由表5 可知，式(28)～(29)的相关系数均小于式(21)的。根据对应雷管段位的数量，可以将炮孔类型分为两大类，其中掏槽孔、周边孔及底板孔仅对应唯一的雷管段位，而辅助孔由段位3、5、7 和9 组成，受多个起爆雷管的影响。由统计数据可知，对仅对应唯一雷管段位的炮孔，尽管式(28)～(29)的拟合效果不如改进公式，但其相关系数大于0.8，可以满足预测精度的基本需要。然而，由段位3～9 雷管组成的辅助眼，通过式(28) 和(29) 得到的相关系数分别为0.646 和0.446，远小于式(21) 的，拟合效果差。

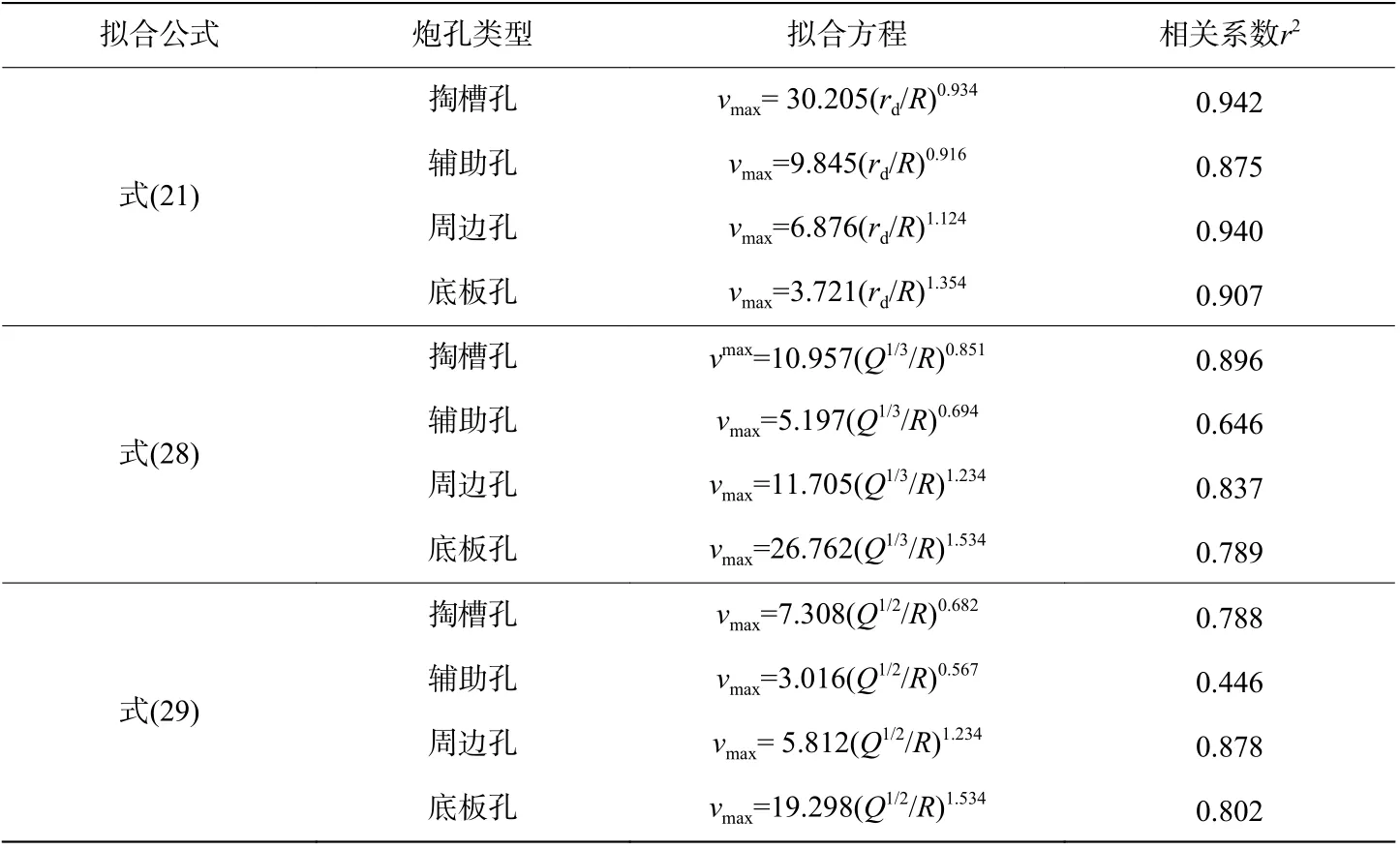
表5 爆破峰值振动速度的拟合效果Table 5 Fitting effects of the blasting peak vibration velocity

以上分析结果证明，爆破振动衰减公式的药量形式对掏槽孔、周边孔、底板孔对应的爆破振动速度的拟合效果较好，但并不适用于由多段雷管组成的辅助孔的振动拟合分析。产生这种差异可能是由于，

掏槽孔、周边孔等起爆主要受单段装药量的影响，而辅助孔由多段雷管组成，对应的爆破振动速度受各段装药量、自由面及雷管段位等多个因素的综合影响，所以若简单以最大单响装药量作为参考变量进行拟合分析并不能反映真实的爆破振动衰减规律。

图10 爆破峰值振动速度采用式(29)的拟合曲线Fig. 10 Fitting curves of equation (29) for the blasting peak vibration velocity

4 结 论

基于Heelan 短柱药包理论，推导了爆破峰值振动速度的衰减公式，并通过量纲分析进行校核。结合隧道爆破工程进行回归分析，得到以下结论。

(1) 基于Heelan 短柱药包理论，引入等效作用半径的概念，理论推导得到适用于隧道爆破振动峰值振速的衰减模型方程，并通过量纲分析验证其可靠性。

(2) 引入等效作用半径作为拟合参变量，不仅可以准确预测不同雷管段位对应的爆破峰值振动速度，而且适用于不同炮孔类型对应的爆破峰值振速的拟合分析。

(3) 推导得到振动衰减模型的药量表达形式，对比发现振速衰减模型的药量表达式的拟合效果不如改进公式。引入改进公式可以综合考虑装药量、装药结构及雷管段位等因素的影响。