一类可图拟阵的二阶圈图的哈密顿性

李亚宁，刘彬，邓梓健，王丽煊，火博丰，2，尹君

（1.青海师范大学数学与统计学院，青海 西宁 810008；2.青海省物联网重点实验室，青海 西宁 810008）

0 引言

拟阵的概念最早是由Whitney［1］在1935年提出的。它是矩阵的向量空间和图的圈空间及键空间的推广。1942年Rado［2］提出了有关拟阵的一些性质，Tutte［3-7］发展了这一概念，并研究了拟阵和图的性质以及拟阵的连通性等问题。1972年Holzmann和Haray［8］研究并证明了拟阵基图的一致哈密顿性。Alspach等［9］研究得到了拟阵基图中路和圈的性质，并证明了简单拟阵的基图是哈密顿连通的边泛圈图。在此之后邓汉元和李荣珩［10］与夏方礼［11］先后研究了拟阵基图的1-哈密顿性与P3-哈密顿性，进一步证明基之间的关系。一个拟阵的基图能够反映该拟阵的不同基之间的变换关系。因此，研究拟阵的基图有助于更好了解拟阵的性质。为了研究连通拟阵中圈的性质，李萍［12］提出拟阵圈图的概念，得出了拟阵圈图的哈密顿性［13-16］、连通度［17］和圈图中圈和路的性质［18］，并把圈图的概念推广为n阶圈图，从而得到了n阶圈图的一些性质。对于一阶圈图的哈密顿性，已经有了一般性的结果：设G=G(M)是一个连通拟阵M的圈图，而且B是M的一个基，则G的连通度［7］κ(G)≥2|E-B|-2。设G=G(M)是一个连通拟阵M的圈图，而且G的最小度是δ(G)，则G的边连通度κ′(G)=δ(G)。设G=G(M)是一个连通拟阵M的圈图，而且M含有至少4个圈，则G是一致哈密顿的［14］。为研究一般连通拟阵的二阶圈图的哈密顿性，本文在拟阵的一阶圈图已有结果基础上，探究了完全二部图K2，n和K3，n的圈拟阵的二阶圈图的哈密顿性。

1 基础知识

定义1［19-20］一个拟阵M是一个有序对(E，ℓ)，其中E是有限集合，ℓ⊆2E是E中子集的集合，满足以下的公理：

（I2）若I∈ℓ，及I⊆I′，则I′∈ℓ；

（I3）若I1，I2∈ℓ，且|I1|＞|I2|，则存在e∈I2-I1使得I1∪e∈ℓ。

集合ℓ中的独立元素成为拟阵M的独立集。设M(E，ℓ)是一个拟阵，若子集X∉ℓ，则令X称为M的一个相关集。极小的相关集为极小圈。令C(M)表示由拟阵M的全体极小圈组成的集合。

定义2［19］对于拟阵M，如果存在某个图G，使得拟阵M同构于图G的圈拟阵，那么称M为可图拟阵。

定义3［12］设拟阵M圈图为G，其中顶点集V(G)=C，边集E(G)={CC′|C，C′∈C，|C∩C′|≠0}，这里C和C′既代表G的顶点，也代表拟阵M的圈。设拟阵M的二阶圈图为G，其中顶点集V(G)=C，边集E(G)={CC′|C，C′∈C，|C∩C′|≥2}，这里C和C′既代表G的顶点，也代表拟阵M的圈。

定义4［21］设G是一个图，如果V(G)可以被划分为集合U和W，使得uw是G的边当且仅当u∈U且w∈W，则称图G为完全二部图。如果|U|=s且|W|=t，那么这个完全二部图有（s+t）个顶点和st条边且可以由Ks，t（或Kt，s）表示。

定义5［20］设G是一个图，包含图G的每个顶点的路称为图G的一条哈密顿路；包含图G的每个顶点的圈称为图G的一个哈密顿圈；如果图G存在一个哈密顿圈，则称之为哈密顿的。如果图G中的每对顶点u，v都存在一条u到v的哈密顿路，则称图G是哈密顿连通的。

定义6［20］对于任意的整数k，且满足3≤k≤n，图G的每对顶点含有长度为k的圈，那么图G就是泛圈图。

定义7［22］设G是一个图，如果G中的任意两个顶点都相邻，则称G是完全图。

定义8［23］设G是一个图，如果对于所有v∈V(G)，有d(v)=k，则图G是k-正则图。

引理1［24］设G是n(n≥3)阶简单图，w是最小度的顶点，如果则G是哈密顿的。

引理2(Menger定理)［21］G是一个顶点数≥k+1的图，图G是k-连通的当且仅当图中任意两个不同的顶点都被至少k条内部不相交的路连接。

2 主要定理

定理1完全二部图K2，n(n≥2)的圈拟阵的一阶和二阶圈图相同，是一个个顶点的(2n-4)-正则图，并且连通度是(2n-4)。

证明显然，在完全二部图K2，n中的圈，是个数恰好等于在这n个点中取两个点的组合数的4-圈，且如果圈与圈之间存在公共边，则公共边的数目为2，因此K2，n(n≥2)的圈拟阵的一阶和二阶圈图是具有个顶点的相同的图。

将K2，n中有两个点的分部中的两个点分别设为O和O′，另一分部中的n个点分别设为1，2，…，n。将经过O，i，O′，j四点的圈标记为{i，j}。则二阶圈图的顶点集合为V(C2(K2，n))={{i，j}|i，j=1，2，…，n，i≠j}。二阶圈图中任何两点{i，j}与{k，l}相邻当且仅当|{i，j}∩{k，l}|=1。对于其中任意一个顶点{i，j}它的邻点为{i，s}，s≠i，j；{j，t}，t≠i，j；s，t∈{1，2，…，n}，共[ ]2(n-2)个。因此完全二部图K2，n(n≥2)的圈拟阵的二阶圈图是(2n-4)-正则图。

对于二阶圈图中任何两点{i，j}与{k，l}，如果它们不相邻，即i，j，k，l各不相同，则有如下（2n-8）条长为3的路连接{i，j}与{k，l}：

{i，j}→{i，s}→{k，s}→{k，l}|；{i，j}→{j，s}→{l，s}→{k，l}|，s∈{1，2，…，n}，s≠i，j，k，l。另有4条长为2的路：

{i，j}→{i，k}→{k，l}|，{i，j}→{i，l}→{k，l}|，{i，j}→{j，k}→{k，l}|，{i，j}→{j，l}→{k，l}|。容易看出这些路的内部点都是各不相同的，因此得到(2n-4)条内部不交的路。

对于二阶圈图中任何相邻两点{i，j}与{j，k}，i，j，k各不相同，则有如下（n-3）条长为3的路连接{i，j}与{j，k}：{i，j}→{i，s}→{k，s}→{j，k}|，s∈{1，2，…，n}，s≠i，j，k。

另 有（n-3）条 长 为2的 路 连 接{i，j}与{j，k}：{i，j}→{j，s}→{j，k}|，s∈{1，2，…，n}，s≠i，j，k。一 条 长 为2的 路 连 接{i，j}与{j，k}：{i，j}→{i，k}→{j，k}。一 条 边 即 长 为1的 路 连 接{i，j}与{j，k}：{i，j}→{j，k}。容易看出这些路的内部点都是各不相同的，因此得到(2n-4)条内部不交的路。

根据引理2得此二阶圈图的连通度为(2n-4)。

定理2完全二部图K2，n(n≥3)的圈拟阵的二阶圈图是哈密顿的。

证明如图1所示，K2，n对应的二阶圈图有个顶点，可表示为V(K2，n)={{i，j}|i，j=1，2，…，n，i≠j}。由拟阵圈图的定义及以上列出的顶点发现，其子集Vi={{i，j}|j=1，2，…，n，i≠j}中任意两个点之间都有边相连，因此由Vi所导出的二阶圈图的子图是完全图，显然，完全图是哈密顿连通的。而i≠j时点集Vi与点集Vj有公共点{i，j}，因此很容易得到此二阶圈图的哈密顿圈。如哈密顿圈表 示 在Vi中{i，j}到{i，s}的一条哈密顿路。因此完全二部图K2，n(n≥3)的圈拟阵的二阶圈图是哈密顿的。

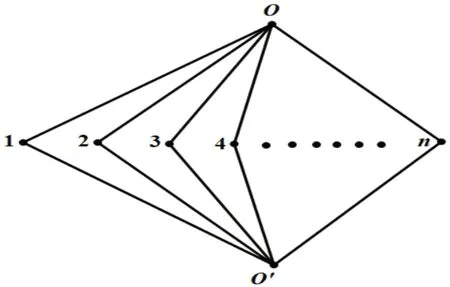
图1 完全二部图K2，nFig.1 Complete bipartite graphs K2，n

定理3完全二部图K2，n(n≥3)的圈拟阵的二阶圈图是泛圈的。

证明针对K2，n的情形，对n用数学归纳法证明。当n=3时，K2，n对应的二阶圈图为完全图K3，显然是泛圈的。假定结论对于n=4，5，…，n-1成立。因此K2，n-1的圈拟阵的二阶圈图是泛圈的。在K2，n-1的二阶圈图中可以找到包含长度从的圈。由定理1和定理2，K2，n的圈拟阵的二阶圈图有个顶点，且是哈密顿的。因此存在经过每个顶点的圈。因为K2，n是由K2，n-1增加（n-1）个顶点{1，n}，{2，n}，…，{n-1，n}得到，且K2，n的顶点{1，2，3，…，n}具有对称性，因此只需要证明对于所有个圈顶点存在包含它的长度从到的圈。

在K2，n-1的二阶圈图基础之上先增加一个顶点{i，n}(i=1，2，…，n-1)，可找到一个包含它的长度为的圈，以此类推，当增加到（n-2）个顶点时，可以找到包含它们的长度为的圈，而即存在长度为的圈。

综上所述，在K2，n的圈拟阵的二阶圈图中存在长度为到的圈。即K2，n(n≥3)的圈拟阵的二阶圈图是泛圈的。

定理4完全二部图K2，n(n≥3)的圈拟阵的二阶圈图是哈密顿连通的。

证明由定理1可得，K2，n对应的二阶圈图有个顶点，将其顶点集表示为V(K2，n)={{i，j}|i，j=1，2，…，n，i≠j}，其子集为Vi={{i，j}|j=1，2，…，n，i≠j}，在其子集中任意两个点之间都有边相连，因此由Vi所导出的二阶圈图的子图是完全图，显然完全图是哈密顿连通的。而i≠j时点集Vi与点Vj有公共点{i，j}，所 以 在 其 二 阶 圈 图 中 可 以 找 到{1，2}→{1，3}→…→{2，3}→{2，4}→…{n-2，n-1}→{n-1，n}的哈密顿路，从而可以发现任意两个顶点都有哈密顿路连接，所以K2，n(n≥3)的圈拟阵的二阶圈图是哈密顿连通的。

定理5完全二部图K3，n(n≥3)的圈拟阵的二阶圈图是哈密顿的。

证明如图2所示，将K3，n中有三个点的分部中的三个点分别设为a，b，c，另一分部中的n个点分别设为1，2，…，n。K3，n的圈都是4-圈和6-圈，4-圈是从a，b，c和这n个点中分别取两个点的组合，所以个数恰好等于。6-圈是将a，b，c与另一个分部中的n个点中任取三个点排列，所以个数恰好等于从n个元中任取三个元的排列数A3n。随着圈个数的增加，顶点的最小度也在逐渐变化，利用引理证明更为复杂。

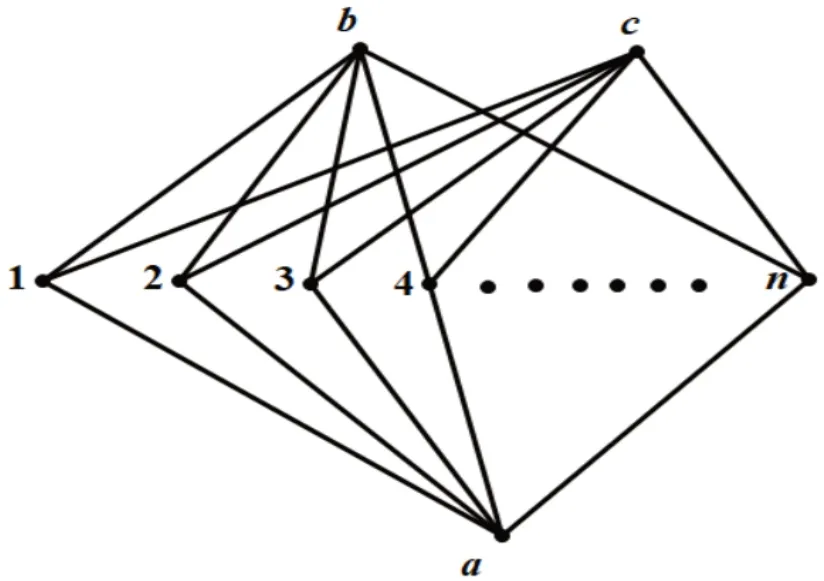
图2 完全二部图K3，nFig.2 Complete bipartite graphs K3，n

因此对n用数学归纳法证明。当n=3时，显然，K3，n对应的二阶圈图是哈密顿的。假定结论对于n=4，…，n-1成立。因此K3，n-1对应的二阶圈图是哈密顿的，其二阶圈图的顶点包括了4-圈和6-圈在二阶圈图中所代表的顶点。其4-圈的个数为个，6-圈的个数为A3n-1个。在其4-圈中含(a，b)，(a，c)，(b，c)的圈分别含有另一个分部的{i，j}(i≠j且i，j=1，2，3，…，n-1)，其6-圈是在一个分部中含有(a，b，c)，另一个分部中含有{i，j，k}(i≠j≠k且i，j，k=1，2，…，n-1)。已知其对应的二阶圈图是哈密顿的，所以其4-圈 与6-圈 作 为 圈 顶 点 在 二 阶 圈 图 中 存 在 哈 密 顿 圈{i，j}→{i，j，k}→{i，j}。K3，n与K3，n-1相比，其4-圈个数增加了[ 3(n-1)]个，6-圈个数增加了[A3n-A3n-1=3(n-1)(n-2)]个。在其4-圈中含(a，b)，(a，c)，(b，c)分别增加了{1，n}，{2，n}，…，{n-1，n}的圈，且此时在新增的4-圈中，在a，b，c分部相同时，圈与圈之间有一个公共元n则有连边；在a，b，c分部不完全相同时，圈与圈在{i，n}(i=1，2，…，n-1)中两个元均相同时才有连边。在其新增的4-圈中可以找到与新增的6-圈中有连边的圈，例如4-圈(a，1，b，n)与6-圈(a，1，b，n，c，i)(i≠1，n)均有连边。且6-圈中若在1，2，3，…，n的分部中若有两个公共元则有连边，即在新增的6-圈中也可以找到连边。所以K3，n的圈拟阵的二阶圈图中存在哈密顿圈，即K3，n(n≥3)的圈拟阵的二阶圈图是哈密顿的。

定理6完全二部图K3，n(n≥3)的圈拟阵的二阶圈图是哈密顿连通的。

证明当n=3时，显然，K3，n对应的二阶圈图是哈密顿连通的，利用K2，n的圈拟阵的二阶圈图是K3，n的圈拟阵的二阶圈图的子图，且在K3，n的6-圈在对应的二阶圈图中所构成的图是完全图的前提下而证明得出的。但发现当n≥5时，其6-圈在对应的二阶圈图中所构成的图不是完全图，因此对n用数学归纳法证明。假设n=4，…，n-1时结论成立，即K3，n-1的圈拟阵的二阶圈图是哈密顿连通的。在K3，n-1的4-圈中含(a，b)，(a，c)，(b，c)的圈分别含有另一个分部的{i，j}(i≠j且i，j=1，2，3，…，n-1)，将其4-圈简记为{i，j}(i≠j且i，j=1，2，3，…，n-1)，其6-圈 是 在 一 个 分 部 中 含 有(a，b，c)，另 一 个 分 部 中 含 有{i，j，k}(i≠j≠k且i，j，k=1，2，…，n-1)，将6-圈简记为{i，j，k}(i≠j≠k且i，j，k=1，2，…，n-1)。所以在其对应的二阶圈图中可以找到从4-圈对应的圈顶点到6-圈对应的圈顶点的哈密顿路{i，j}→{i，j，k}。

那么K3，n与K3，n-1相比，4-圈中含(a，b)，(a，c)，(b，c)的圈分别新增了{1，n}，{2，n}，…，{n-1，n}的圈，在新增的4-圈对应的圈顶点中可以找到连边的顶点，即{1，n}→{2，n}→…→{n-1，n}。在其6-圈中新增了含有n的顶点，6-圈与6-圈在1，2，3，…，n中若有两个公共元则有连边，且在新增的4-圈与6-圈中若含有n以及其它公共元，则可以找到连边，所以在K3，n的圈拟阵的二阶圈图中同样可以找到从4-圈到6-圈的哈密顿路{i，j}→{i，j，k}，此时i≠j≠k且i，j，k=1，2，…，n。

综上所述，K3，n的圈拟阵的二阶圈图是哈密顿连通的。

猜想1完全二部图K2，n和K3，n的圈拟阵的二阶圈图是具有一致哈密顿性的。