上三角算子矩阵的Browder谱和Drazin谱

青梅

（呼和浩特民族学院数学与大数据学院，内蒙古 呼和浩特 010051）

0 引言

Hilbert空间H=H1⊕H2上的有界线性算子T可表示为2×2的算子矩阵形式其中Tij：Hj→Hi，i，j=1，2。特别地，若H1是T的不变子空间，则T21=0。此时，T是上三角算子矩阵。近年来，很多学者研究Hilbert空间H⊕K上三角算子矩阵各类谱性质。文献［1-7］利用局部谱理论估计了集合Dσ*：=(σ*(A)∪σ*(B))σ*(MC)，并刻画了对任意的C∈B(K，H)等式

成立的充分条件，其中σ*包含谱、本质谱、Weyl谱、Browder谱和Drazin谱等。文献［8］利用Fredholm理论和谱集分类，更精细地刻画了集合Dσ*的分布范围，并给出了等式（1）成立的充要条件，其中σ*={σe，σw，σb}。文献［9］中得到的是无界上三角算子矩阵的谱，近似点谱和亏谱的类似性质。注意到，这些充要条件不仅与对角算子有关，也与算子矩阵本身有关。进一步，文献［10］将有界情形结论推广至无界情形，利用扰动理论和谱集分类描述了集合Dσe，Dσw的分布，并刻画了无界上三角算子矩阵的本质谱和Weyl谱的并集等于对角算子相应谱并集的充要条件。值得注意的是，这些充要条件只与对角算子有关。然而，未见有界或无界情形的Browder谱和Drazin谱类似结论。

本文主要研究有界上三角算子矩阵MC的Browder谱和Drazin谱性质。利用Fredholm理论和谱集分类估计集合Dσb、DσD的分布范围，再利用扰动理论给出MC的Browder谱和Drazin谱满足等式（1）的充要条件，进而推广前人的结论。此外，结合文献［9］的结论和扰动理论得到了MC的谱满足等式（1）的充要条件。本文中刻画的这些充要条件都只与对角算子A和B有关。

先给出文中涉及的符号和定义。设H和K均为无穷维复可分的Hilbert空间，B(H，K)表示从H到K的所有有界线性算子集合。若K=H，则通常简记为B(H)。一般T∈B(H)的共轭算子，零空间和值域分别记为T*，N(T)，R(T)。将零空间N(T)和商空间H/R(T)的维数分别记为α(T)和β(T)。若R(T)是闭集且α(T)＜∞（β(T)＜∞），则称T是左（右）Fredholm算子；若T是左或右（左且右）Fredholm算子则称T是半Fredholm（Fredholm）算子。当α(T)和β(T)至少有一个有限时，可定义T的指标ind(T)：=α(T)-β(T)。若T是Fredholm算子且ind(T)=0，则称T是Weyl算子。T的升标和降标记为

若下确界不存在，则升标asc(T)或降标dsc(T)为无穷大。若T是左（右）Fredholm算子且asc(T)＜∞(des(T)＜∞)，则称T是左（右）Browder算子；若T是左且右Browder算子，则称T是Browder算子。若存在正整数k和算子S∈B(H)满足TkST=Tk，STS=S，TS=ST，则称T是Drazin可逆算子。不难发现，T是Drazin可逆算子当且仅当asc(T)＜∞且des(T)＜∞。若asc(T)＜∞且R(Tasc(T)+1)是闭集，则称T是左Drazin可逆算子；若des(T)＜∞且R(Tdec(T))是闭集，则称T是右Drazin可逆算子。

T的左Browder谱、右Browder谱、Browder谱、左Drazin谱、右Drazin谱、Drazin谱分别定义为

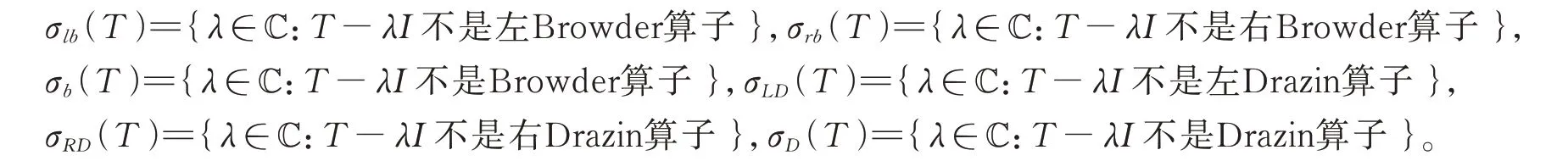
记T的谱，近 似点 谱和 亏谱 分别 为σ(T)，σap(T)，σδ(T)。此外，引入点谱σp(T)和剩余谱σr(T)的子集［9，11］：

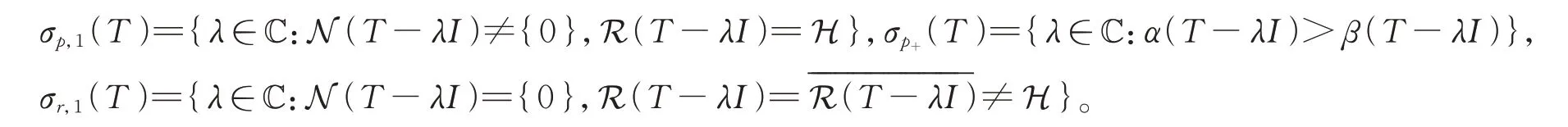
显然σ(T)=σap(T)∪σr，1(T)=σδ(T)∪σp，1(T)，且σp，1(T)⊂σp+(T)⊂σp(T)，σr，1(T)⊂σr(T)。

文中将复平面C内的集合S的孤立点集、聚点集、内部、边界分别记为isoS，accS，intS，∂S。

1 主要结论及其证明

给出主要结论之前先列出所用到的一些引理。

引理1［12］设T∈B(H)，则如下结论成立：

(1)若asc(T)＜∞，则α(T)≤β(T)；(2)若dsc(T)＜∞，则β(T)≤α(T)；(3)若asc(T)=dsc(T)＜∞，则α(T)=β(T)；(4)若α(T)=β(T)＜∞且asc(T)＜∞或dsc(T)＜∞是有限的，则asc(T)=dsc(T)。

引理2［6，13］设∈B(H⊕K)，则如下结论成立：

(1)若A、B、MC三者中任意两者是Browder算子，则第三者也是Browder算子；(2)若A、B、MC三者中任意两者是Drazin可逆算子，则第三者也是Drazin可逆算子。

1.1 MC的Browder谱性质

定理1设A∈B(H)和B∈B(K)是给定算子，则对任意的C∈B(K，H)成立等式

证明先证明等式（2）左边包含于右边。设λ∉σb(MC)∪(σp+(A*)*∩σp+(B))，则λ∉σb(MC)∪σp+(A*)*或λ∉σb(MC)∪σp+(B)。若λ∉σb(MC)∪σp+(A*)*，则A-λI是 左Fredholm算 子，asc(A-λI)＜∞，且α(A-λI)≥β(A-λI)。由引理1，可得α(A-λI)≤β(A-λI)。于是α(A-λI)=β(A-λI)＜∞。再由引理1，可知A-λI是Browder算子。进一步，根据引理2，可得B-λI也是Browder算子。因此λ∉σb(A)∪σb(B)。若λ∉σb(MC)∪σp+(B)，则同理可证λ∉σb(A)∪σb(B)。

反之，设λ∉σb(A)∪σb(B)，即A-λI和B-λI都是Browder算子。由引理1，可知ind(A-λI)=ind(B-λI)=0。因此λ∉σp+(A*)*∩σp+(B))。再由引理2，可得λ∉σb(MC)。于是等式（2）左边包含右边。

注1由定理1的证明可知，等式（2）可改写为

定理2设A∈B(H)和B∈B(K)给定算子，则对任意的C∈B(K，H)成立等式

当且仅当λ∈(σp+(A*)*σlb(A))∩(σp+(B)σrb(B))，蕴含α(A-λI)+α(B-λI)≠β(A-λI)+β(B-λI)。

证明设(σp+(A*)*σlb(A))∩(σp+(B)σrb(B))≠。由推论1可得，等式（3）成立当且仅当对任意的C∈B(K，H)，有(σp+(A*)*σlb(A))∩(σp+(B)σrb(B))⊂σb(MC)，即

再由固有Browder谱的表达式［14］

可易推出结论成立。

注2定理1更精细地刻画了集合Dσb的分布。而定理2中所描述的等式（3）成立的充要条件仅仅与MC的对角算子有关。显然，这些结论是文献［8］中定理3.3的推广。

结合文献［9］中的推论2和固有谱集合，可得到MC的谱满足等式（1）的充要条件。

定理3设A∈B(H)和B∈B(K)是给定的算子，则对任意的C∈B(K，H)成立等式

当且仅当λ∈σp，1(B)∩σr，1(A)蕴含α(B-λI)≠β(A-λI)。

证 明由 文 献［9］推 论2可 知，对 任 意 的C∈B(K，H)等 式（4）成 立 当 且 仅 当

1.2 MC的Drazin谱性质

定理4设A∈B(H)和B∈B(K)是给定的算子，则对任意的C∈B(K，H)成立等式

证明由引理2和包含关系σp，1(B)⊂σD(B)，σr，1(A)⊂σD(A)，可知等式（5）的左边包含于右边。

反之，设0∈(σD(A)∪σD(B))σD(MC)，则MC为Drazin可逆算子。于是存在ε＞0，对任意的满足的0＜∣λ∣＜ε的λ，可 推 出MC-λI是 可 逆 算 子。从 而A-λI是 左 可 逆 算 子 且B-λI是 右 可 逆 算 子，即λ∉σap(A)∪σδ(B)。于是0∉accσap(A)且0∉accσδ(B)。假设0∉σp，1(B)∩σr，1(A)，则需考虑如下两个情形。

情形I若0∉σp，1(B)，则0∈ρ(B)∪σδ(B)。(i)若0∈ρ(B)，可推出B是Drazin可逆算子，再由引理2，可 得A也 是Drazin可 逆 算 子，与0∈σD(A)∪σD(B)矛 盾；(ii)若0∈σδ(B)，则0∈isoσδ(B)。由isoσ(B)⊂∂σ(B)⊂σδ(B)∩σap(B)，可知0∈isoσ(B)。又因为des(B)＜∞，根据文献［15］定理10.5，可得B是Drazin可逆算子。进而可知A也是Drazin可逆算子，与0∈σD(A)∪σD(B)矛盾。

情 形II当0∉σr，1(A)时，由σr，1(A)=σp，1(A*)*，σap(A)=σδ(A*)*以 及A和A*的Drazin可 逆 等 价性，同理可得出与0∈σD(A)∪σD(B)矛盾的结论。故等式（5）的左边包含右边。

注3定理4更精确地刻画了集合DσD的分布范围。不难发现文献［7］中定理2.1和推论2.2—2.4是该结论的推论。下面给出文献［7］中推论2.5的推广形式。

推论1设A∈B(H)和B∈B(K)是给定的算子，则

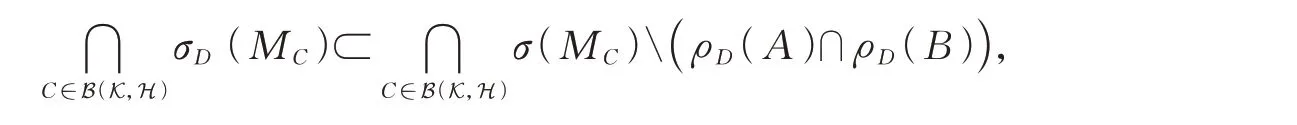
其 中ρD(A)=CσD(A)，ρD(B)=CσD(B)。特 别 地，若5个 等 式σp，1(B)∩σr，1(A)=，σp，1(B)=，σr，1(A)=，intσp，1(B)=，intσr，1(A)=之一成立，则

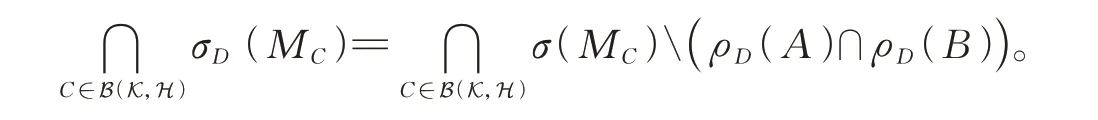
该推论证明类似于文献［7］推论2.5的证明，略证。进一步，文献［16-17］更精细地估计了固有Drazin谱的分布范围

下面给出MC的Drazin谱满足等式（1）的充要条件。

定理5设A∈B(H)和B∈B(K)是给定的算子，则对任意的C∈B(K，H)成立等式

当且仅当λ∈σp，1(B)∩σr，1(A)蕴含α(B-λI)≠β(A-λI)。

证 明先 证 明 必 要 性。若 等 式（6）成 立，则 根 据 定 理4，可 得 对 任 意 的C∈B(K，H)有σp，1(B)∩σr，1(A)⊂σD(MC)，即。再根据固有Drazin谱的分布，有

再证充分性。若λ∈σp，1(B)∩σr，1(A)，可推导出α(B-λI)≠β(A-λI)，则对任意的C∈B(K，H)，等式（4）成立。再根据文献［7］推论2.4可知，等式（6）也成立。根据上述定理可得出等式（3），（4）和（6）之间的关系。

定理6设A∈B(H)和B∈B(K)是给定算子。则

(1)下列3个条件等价：

(2)若σb(MC)=σb(A)∪σb(B)，则σ(MC)=σ(A)∪σ(B)且σD(MC)=σD(A)∪σD(B)。

证明(1)证明显然。

(2)若λ∈σp，1(B)∩σr，1(A)，则λ∈(σp+(A*)*σlb(A))∩(σp+(B)σrb(B))。由 已 知 条 件 和 定 理2，可 知α(A-λI)+α(B-λI)≠β(A-λI)+β(B-λI)。因 为α(A-λI)=0且β(B-λI)=0，于 是α(BλI)≠β(A-λI)。再根据本定理结论（1），结果显然。

2 例子

例1定 义 算 子A，B，C∈B(l2)为：A(x1，x2，x3，…)=(x1，0，x2，0，x3，…)，B(x1，x2，x3，…)=(x2，x4，x6，…)，C(x1，x2，x3，…)=(0，x1，0，x3，0，x5，…)。

容 易 验 证R(A)和R(B)都 是 闭 集 且α(A)=0，β(A)=∞，α(B)=∞，β(B)=0。则0∈σp，1(B)∩σr，1(A)且0∈(σp+(B)σlb(B))∩(σp+(A*)*σrb(A))。但 是α(A)+α(B)=α(B)=β(A)=β(A)+β(B)。根据定理2，3和5，可知等式（3），（4）和（6）不成立。

另一方面，不难验证MC是双射，从而0∉σ*(MC)。但是0∈σ*(A)∪σ*(B)。其中σ*∈{σb，σD，σ}。因此σ*(MC)≠σ*(A)∪σ*(B)。

例2定义算子A，B，C∈B(l2)为：A(x1，x2，x3，…)=(0，x1，x2，x3，…)，B(x1，x2，x3，…)=(x2，x3，x4，…)，C(x1，x2，x3，…)=(x1，0，0，…)。

注意到MC是双射。从而0∉σ*(MC)，其中σ*∈{σb，σD，σ}。而R(A)和R(B)都是闭集且α(A)=0，β(A)=1，α(B)=1，β(B)=0。于是可推导出0∈σ*(A)∪σ*(B)。根据定理2，3和5，可知存在λ1，λ2，满 足λ1∈(σp+(B)σlb(B))∩(σp+(A*)*σrb(A))，λ2∈σp，1(B)∩σr，1(A)，但 是α(A-λ1I)+α(B-λ1I)=β(A-λ1I)+β(B-λ1I)，α(B-λ2I)=β(A-λ2I)。

另一方面，取λ1=λ2=0即可。易验证0∈σp，1(B)∩σr，1(A)且0∈(σp+(B)σlb(B))∩(σp+(A*)*σrb(A))，但成立如下等式α(A)+α(B)=α(B)=β(A)=β(A)+β(B)=1。