Orlicz空间中Meyer-könig-Zeller-Kantorovich算子的加Jacobi权逼近

姜胜楠，吴嘎日迪，2

（1.内蒙古师范大学数学科学学院，内蒙古 呼和浩特 010022；2.内蒙古自治区应用数学中心，内蒙古 呼和浩特 010022）

0 引言

Meyer-könig-Zeller-Kantorovich算子由V.Totik在1983年的文献［1］引入如下：

其中

权函数w(x)=xα(1-x)β，-1＜α，β＜1，φ(x)=x(1-x)。

本文研究Meyer-könig-Zeller-Kantorovich算子加Jacobi权情况在Orlicz空间中的逼近问题，用M(u)和N(v)表示互余的N函数，有关于N函数的定义及性质详情可见文献［2］中的论述。定义Orlicz空间中的范数：

由具有有限Orlicz范数的可测函数的全体{u(x)}构成了N函数M(u)生成的Orlicz空间其中表示v(x)关于N(v)的模。由文献［2］知，Orlicz范数还可定义为

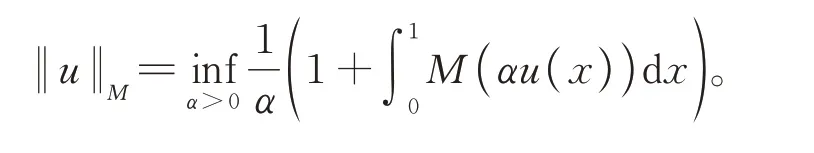
在此之前该算子在Lp空间内的加权逼近的特征刻划已由文献［3］得出，但在Orlicz空间中有关该算子加Jacobi权的逼近问题研究较少。本文利用Hölder不等式，凸函数的Jensenn不等式以及Orlicz空间中K-泛函与连续模给出了该算子在Orlicz空间中加Jacobi权的逼近的特征刻划。

1 相关引理及证明

引理1设wf∈L*M[0，1]，则

这里

C表示与x和n无关的常数（文中不同处C值可能不同）。

证明由文献［3］知，当时有

其中l∈N，m∈Z。且容易算出

因此有

引理1得证。

引理2设则‖

证明由文献［3］计算有

计算有

此外，

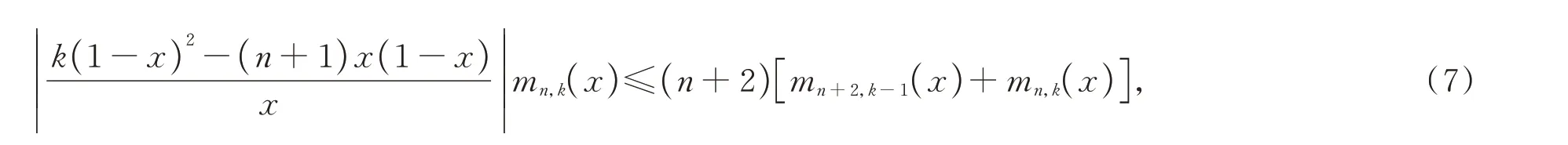
引理3令

则

证明由文献［3］先假设

令

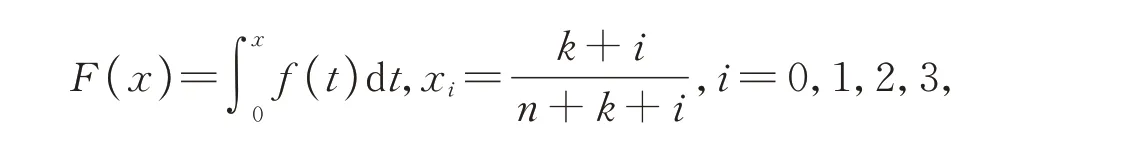
经计算有

根据Taylor公式有

将x=x1，x2，x3分别带入Δn，k F的表达式有

由文献［3］和式（8）有

所以有

显然对P2由引理1可以直接得出又由文献［3］和式（8）有

且由文献［4］有

其中γ(x)=(1-x)。由此即得

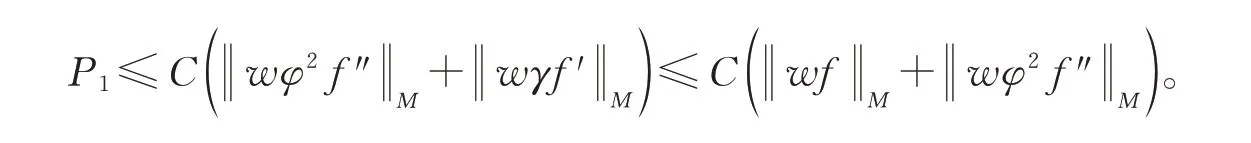
对∀f∈Dw，令

其中g，(f-g)∈Dw，显然当时，(f-g)′=0。

并且计算有

通过上述结果及引理1，有

引理3证毕。

引理4设f∈Dw，则

证明因为

其中

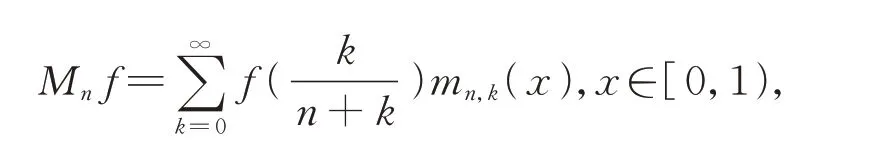
则有

因为Mn(t-x；x)=0，且有

所以用最大值函数L(·；·)表示有

此处

综上所述引理4得证。

2 主要结论

加权K-泛函定义为

定理设w(x)f(x)∈L*M[0，1]，0＜α＜1，则下列各式是等价的：

证明由引理1—4及文献［4-5］的结果可得（1)⇔(2)，由文献［1］可得出(2)⇔(3)，定理证毕。