S-度量空间中(ψ-)φ-弱压缩多值映射的不动点定理

李兆辉，杨理平

（广东工业大学 数学与统计学院，广东 广州，510520）

1 引言及预备知识

不动点理论在非线性泛函分析中占有重要地位. Banach率先提出的Banach不动点定理是度量空间理论中的重要工具，它保证了完备度量空间中自映射不动点的存在性和唯一性，并为寻找这些不动点提供了一种建设性的方法. 1969年，Nadler[1]将Banach压缩定理推广到多值压缩映射的不动点. 1973年，Markin[2]研究了Hausdorff度量空间中多值压缩映射的不动点定理. 此后，关于多值压缩映射的不动点定理得到了多方面的发展[3-8]. 1997年，Alber[9]提出了φ-弱收缩映射. 最近，Saluja[10]在S-度量空间中建立了(ψ-)φ-弱压缩映射不动点定理. 此外，还有一些学者在该课题上推广不动点定理[11-12]. 一些学者结合(ψ-)φ-弱压缩映射和多值映射的概念，探讨在此类条件下的不动点问题[12-14].

本文受到文献[7]和[10]的启发，将多值映射的概念和(ψ-)φ-弱压缩映射结合到S-度量空间，建立了一些不动点定理.

定义1[15]260设X是非空集. 若映射满足：

2）S（x,y,z）=0，当且仅当

则称S是X的一个度量，(X,S)为S-度量空间.

引理1[15][260]设(X,S)为S-度量空间，对于任意有

定义2[15][261]设(X,S)为S-度量空间.

1）我们称序列｛xn｝⊂X收敛到x∈X，如果满足

2）若对于任意ε＞0，存在n0∈N，当n,m≥n0时，有，则称序列｛xn｝为柯西列.

3）若在X中所有的柯西列收敛，则称(X,S)为完备的S-度量空间.

引理2[16]设(X,S)为S-度量空间，若序列｛xn｝,｛yn｝⊂X满足，那么有

受文献[4]在度量空间定义的Hausdorff度量启发，在本文中，设CB(X)为完备S-度量空间中的非空闭子集，由S-度量空间诱导在CB(X)上的Hausdorff度量定义为

令映射f:X→CB(X)为(X,S)上的闭多值映射，映射T:X→X为(X,S)上的单值映射，那么

1）x∈X是T的一个不动点，如果Tx=x，x∈X是f的一个不动点如果x∈fx；

2）x∈X是f和T的一个公共不动点，如果

定义3[7]映射是连续的，如果且时有

定义4[10]设(X,S)是S-度量空间. 自映射T:X→X称为(ψ- )φ-弱压缩映射如果对于一切x,y∈X时，

本文结合多值映射的概念，推广和改进了文献[10]讨论的S-度量空间中(ψ-)φ-弱压缩映射的不动点定理.

2 主要结果

定理1设(X,S)是完备S-度量空间. 若存在z∈fx，w∈fy满足

其中

ψ和φ是连续非增函数，当且仅当t=0，L≥0. 那么f在X上有不动点.

证任取x0∈X，存在x1,x2∈X，使得以此类推，则存在序列｛xn｝⊂X，使得其中n∈ ｛0 ,1,2,…｝.

由不等式（1）有

其中

综 上 分 析 有S(xn,xn,xn+1) ≤M(xn-1,xn-1,xn)≤2S(x n-1,x n-1,xn). 即 序 列｛S(xn,x n,xn+1)｝是 单 调 非 增 且 有界的. 则存在r≥0，有

于是，在不等式（2）中令n→∞，有φ(r) ≤φ(r)-φ(r)，当且仅当r=0时成立，否则矛盾. 因此

接下来证明｛xn｝是柯西列. 假设存在N∈N，当m＞n＞N时，有

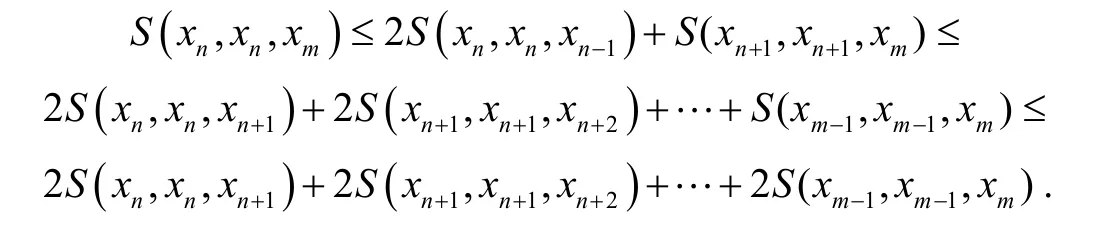
令上式n→∞，那么n,m→∞，有因此，序列｛xn｝是柯西列.

由CB(X)的完备性以及｛xn｝是在CB(X)上的柯西列可知，存在x∈CB(X)，使得另外，我们可以找到y∈fx，使得

其中

除外，由于y∈fx，我们有

则ψ(S（x,x,y）)=0，即S（x,x,y）=0. 因此有x∈fx，即f在X上有不动点. 证毕.

注1在定理1中，通过修改条件和构造新的不等式，将文献[7]中定理2.1的b-度量空间推广到S-度量空间；将文献[10]中定理3.2的自映射推广到多值映射.

推论1 设(X,S)是完备S-度量空间. 若存在z∈fx，w∈fy满足

其中ψ和φ是连续非增函数，当且仅当t=0. 那么f在X上有不动点.

定理2设(X,S)是完备S-度量空间，TX是X上的完备子集，fX⊂TX. 若映射T:X→X和多值映射f满足

其中

ψ和φ是连续非增函数当且仅当t=0，L≥0. 那么f和T在X上有一个叠合点z∈X，而且，如果TTz=Tz，那么f和T有一个公共不动点.

证令x0∈X，我们可以构造序列｛xn｝⊂X如下：由于fx0⊂TX，存在一点x1∈X使得Tx1∈fx0，以此类推，我们可以得到序列｛x n｝ :Txn∈fxn-1，其中对于n∈ ｛1 ,2,…｝. 由不等式（7）有

其中

于是，在不等式（8）中令n→∞，有当且仅当r=0时成立，否则矛盾. 因此

接下来证明｛Txn｝是柯西列. 假设存在N∈N，当m＞n＞N时，有

令上式n→∞，那么n,m→∞，有因此，序列｛Txn｝是柯西列.

由CB(X)的完备性以及｛Txn｝是在CB(X)上的柯西列可知，存在z∈CB(X)，使得由S-度量空间的三角不等式得

由不等式（7）得

其中

令不等式（11）和（12）中n→∞，有

假设S(Tz,Tz,fz)＞0，有然后，令不等式（9）中n→∞，有

矛盾. 因此S(Tz,Tz,fz)=0. 因为fz是闭集，所以有Tz∈fz. 因此，T和f在X上有叠合点z.

下证Tz是f在X上的公共不动点. 由有

其中

注2在定理2中，通过构造新的不等式将文献[5]中定理3.4从度量空间推广到S-度量空间.

3 结论

本文运用了多值映射的概念，在S-度量空间定义了Hausdorff度量. 另外，通过改进（ψ-φ）-弱压缩型函数，提出满足此条件公共不动点问题，探讨出在（ψ-φ）-弱压缩映射多值函数的情况下，其不动点是存在的，所得结果为多值映射在S-度量空间相关不动点定理的推广.