升沉补偿系统多目标构型优化
洪 黎,柏文峰,张 超,钱于杰
(1.中国航发控制系统研究所,江苏 无锡 214100;2.北京航空航天大学 自动化科学与电气工程学院,北京 100191)
引言
海上作业由于受到海浪、海风、海潮、洋流等各种恶劣海洋条件的影响,海洋作业装备会随之产生升沉运动,严重威胁海上作业的安全性,同时也会缩短海洋作业的窗口期,降低海上作业的效率。升沉补偿系统的目的是为了实现海洋作业设备运动和海浪运动的解耦,可以有效地降低海洋装备升沉运动对于海洋作业的各种影响。目前,国内外已经有很多关于升沉补偿系统控制算法和性能仿真的研究[1-5]。
WOODACRE J K等[6]为主动升沉补偿系统设计了模型预测控制器(Model-predictive Controller,MPC),克服了四位三通阀的滞后、死区和非线性特性等问题。LI S等[7]为了减少船舶意外升沉变化对水下有效载荷响应的不利影响,特别设计了一种具有非线性串联控制器的混合主动-被动升沉补偿(HAHC)系统。DO K D等[8]设计了一种采用非线性控制器的双杆电静液作动器驱动的主动升沉补偿系统,控制系统通过调节立管上端到海床的距离来减少船舶升沉运动对立管响应的影响。KUCHLER S等[9]为了解决主动升沉补偿系统传感器和执行器之间时间延迟的问题,首先提出了一种船舶垂直运动的预测算法,使用前馈控制器为液压驱动绞车制定了一种基于反转的控制策略,使得有效载荷的运动与船舶的运动分离。
随着升沉补偿系统的发展,补偿效率不再是评价其好坏的唯一标准。作为海洋作业的重要一环,升沉补偿系统的稳定性和可靠性越来越受到用户的关注。同时,升沉补偿系统作为一款商品,成本因素是其不可忽略的一个竞争力因素。在升沉补偿系统结构和控制方法日趋成熟的背景下,对于考虑多目标优化情况下的升沉补偿结构优化研究,可以使升沉补偿系统在补偿效率、成本、可靠性等各个方面都获得较好的指标,更加有利于升沉补偿系统高效、健康、低成本的稳定运行,也有利于推动其商业化发展。
在升沉补偿系统优化方面,国内外进行了相关的研究,主要集中在控制系统参数的优化和系统机械结构的优化两方面[10]。升沉补偿系统的补偿效果与控制参数的选择有关,ZHOU M等[11]建立了基于遗传PID控制算法的波浪补偿系统控制框图,采用遗传粒子群优化算法,通过交叉和变异算子对最优指标和PID参数进行优化。TANG G等[12]利用粒子群算法优化了升沉补偿系统控制器的控制参数,该算法使得系统超调小、响应快。在升沉补偿系统机械结构的优化方面,GU P等[13]为海上起重机开发了一种主动升沉补偿系统设计方法,将成本和性能因素纳入设计阶段;ZHANG Y等[14]为减小支撑腿的伸展范围,同时降低补偿平台上甲板的工作高度,对补偿平台的结构进行了优化,并设计了一种新型的3-SPR并行平台。
国内也对升沉补偿系统的优化进行了一定的研究。吴倩[15]用AMESim对绞车升沉补偿系统进行参数敏感性分析,分别研究了绞车转动惯量、蓄能器体积、初始压力以及负载因素对补偿效果的影响。李晓东等[16]对3种常见的天车升沉补偿系统进行分析比较,对性能较差的系统进行了优化升级,并通过仿真验证了优化结果的有效性。刘振东等[17]对比了3套不同的天车升沉补偿系统摇摆装置经典设计方案,分别建立其数值模型,基于线性加权法建立其影响因素权重表和综合评价标准,从而实现了3套方案中的评价选优。刘香福[18]将海浪补偿模拟系统的结构参数作为决策变量,将全局调整指标和全局操作指标作为目标函数,采用序列二次规划算法进行参数优化。熊云峰等[19]综合运用层次分析法、变异系数法、加权-灰色TOPSIS法,解决了天车型升沉补偿系统中摇摆装置构型优选问题。
本研究在对主被动复合式升沉补偿系统的工作原理进行分析的基础上,结合设计要求,提出了升沉补偿系统多目标优化的设计方法,以可靠性、成本和补偿效率为目标函数,综合应用非支配排序和层次分析方法获得了升沉补偿系统的最优构型。
1 升沉补偿系统构型分析
1.1 优化对象分析
主被动复合式升沉补偿系统多目标构型优化的第一步为构型搜索,首先需要对主被动复合式升沉补偿系统的结构进行分析。根据设计需求,所研究的升沉补偿系统是为了应对4级海况,对应浪高度范围为1.25~2.50 m。
液压系统具有驱动功率密度大、快速性好等优点,常作为升沉补偿系统的驱动方式。ZHANG C等[20-21]对某型主被动复合式升沉补偿系统液压系统的原理进行了详细的分析,并将其分为能源系统和补偿装置,其中能源系统为升沉补偿系统的正常工作提供能源支持,能源系统中的蓄能器和泵属于关键部件且重要度较高,对系统的安全可靠运行非常重要。因此本研究从提高升沉补偿系统可靠度的目的出发,对液压泵和蓄能器采用冗余设计,从而提高系统整体的可靠度,延长系统的工作时间。
船用升沉补偿系统考虑到离岸工作的特点及高可靠性的需求,在补偿装置层面上多采用系统级冗余的策略,如图1所示。本研究所考虑的升沉补偿系统需要设置2套补偿装置,即补偿装置1和补偿装置2。根据前期的需求分析和后续的目标函数约束,补偿装置1和补偿装置2可采用相似冗余设计,也可采用非相似冗余设计。在某个具体的补偿装置中,不同类型的液压缸与控制阀组的组合也可以进行优化设计。采用硬件余度的可靠性设计技术可以提高升沉补偿系统的可靠性,为海上作业提供更加可靠、安全的支撑。
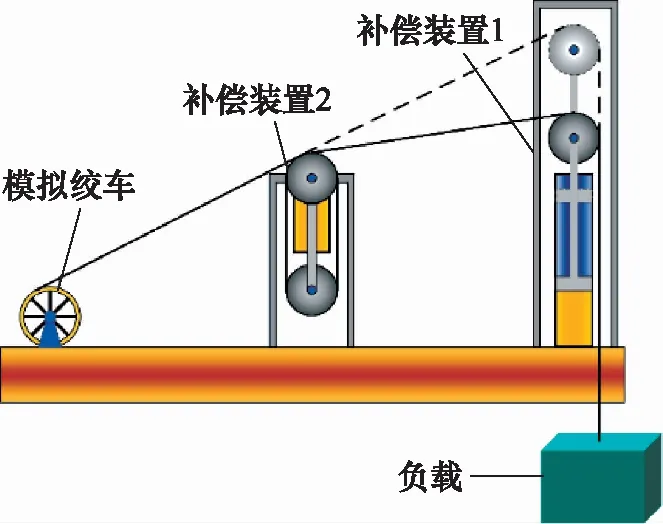
图1 补偿装置整体构型
1.2 基本构型
补偿装置是升沉补偿系统的核心,直接影响着系统的补偿效率,不同的补偿装置在部件类型、连接方式等方面上存在差异,图2~图4为3种不同的补偿装置构型。
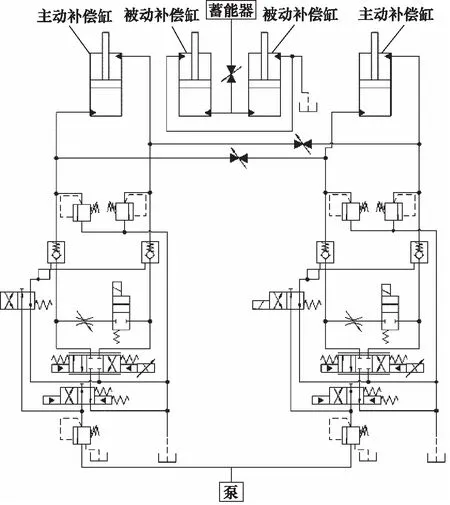
图2 补偿装置构型1
图2中为构型1,编号DC1。被动补偿缸和主动补偿缸均采用活塞缸,2个控制阀组分别控制2个主动补偿缸,实现4个活塞杆的同步伸缩。
图3为构型2,编号DC2,是构型1的缩减版,1个控制阀组控制2个主动补偿缸。由于仅采用1个控制阀组,最大流量为构型1的1/2,在应对低等级海浪时补偿效率不受影响,在面对恶劣海况时,补偿效率会下降。
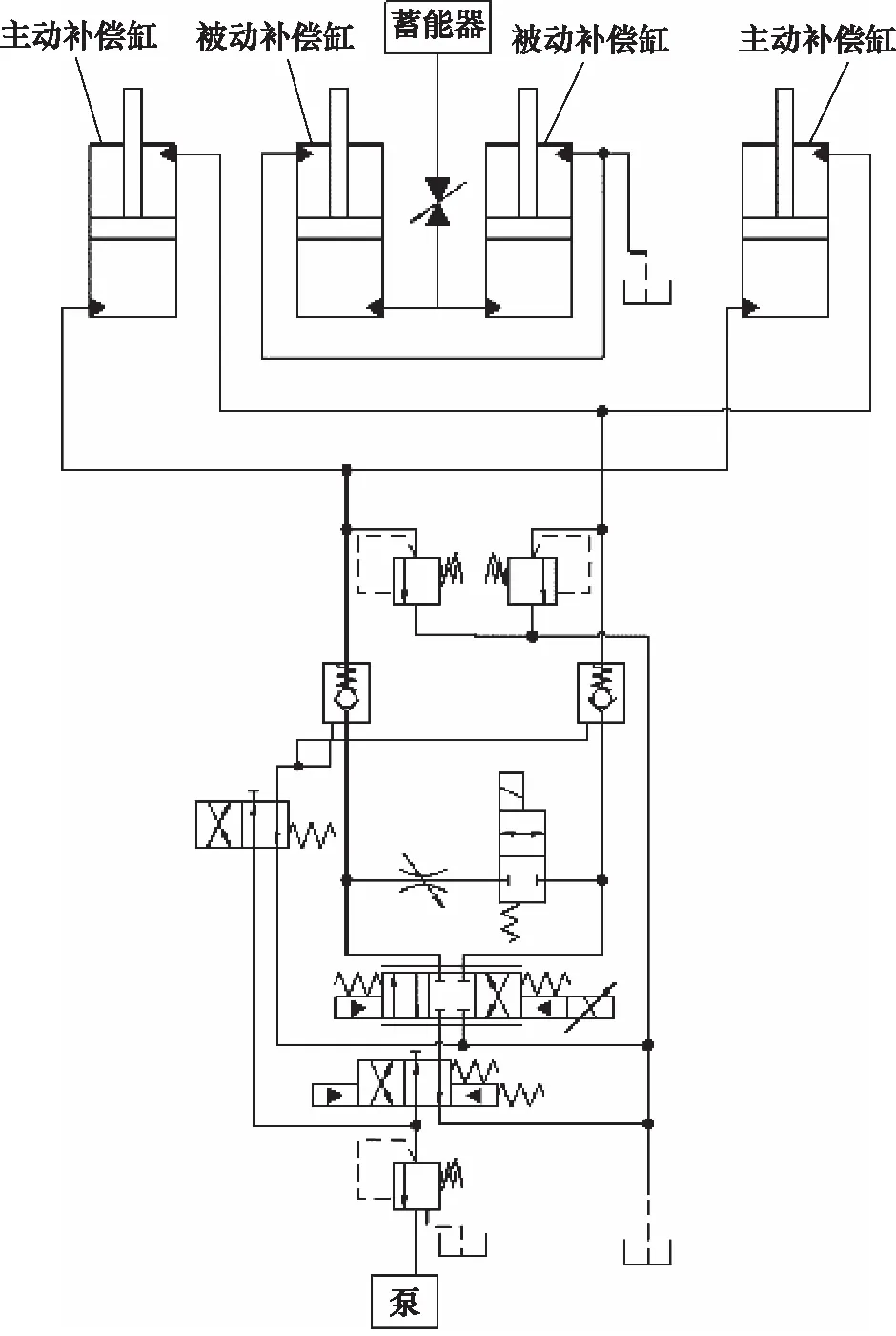
图3 补偿装置构型2
图4为构型3,编号DC3。被动补偿缸采用活塞缸,而主动补偿缸采用柱塞缸。由于柱塞缸具有只能伸出不能缩回的特点,因此控制阀组两端分别连接被动补偿缸的有杆腔和主动补偿缸。当控制阀组向主动补偿缸供油时,实现所有液压缸同步伸出;当控制阀组向被动补偿缸无杆腔供油时,实现所有液压缸同步缩回。

图4 补偿装置构型3
在3种构型中,控制阀组采用相同结构设计,减压阀起到减低压力的作用,2个电磁换向阀起到安全阀的作用,只有两者同时通电,系统才能正常工作。伺服阀接收控制信号,控制液压缸的伸出和缩回,实现升沉补偿的目的。节流阀和电磁开关阀共同作用,在系统启动和关闭时起到导通和缓冲的作用。
在补偿装置中,液压缸的行程决定了补偿装置的最大补偿能力,液压缸的行程越长,补偿装置可应对的海况等级越高。在本研究所讨论的3种构型的补偿装置中,液压缸的行程是根据4级海况要求设计的,其行程取浪高的典型值,即2 m。升沉补偿系统的补偿效率由补偿装置构型和控制方式直接决定,也受到液压泵、蓄能器等因素的影响。
泵在不同构型的差别为冗余数量的差别,如表1所示。本研究分别考虑1台泵、2台泵和3台泵的情况。由升沉补偿系统的工作原理可知,泵的流量会影响补偿效率,当海况等级较为恶劣时,海浪高度变化速度快,对于液压缸的活塞缸的伸出或者缩回的速度要求也相应提高。流入液压缸的流量决定了液压缸作动的快慢,泵为液压缸的作动提供流量,不同构型的泵组合在流量供给能力上存在差异。本研究的泵最大流量为100 L/min,若3台泵共同作用,则最大供油流量为300 L/min。在面对高度较低的海浪时,1台泵的流量足以支撑整个系统的流量需求,其余泵可作为冗余备份。在面对恶劣海况时,多台泵共同作用,可以提高补偿效率。
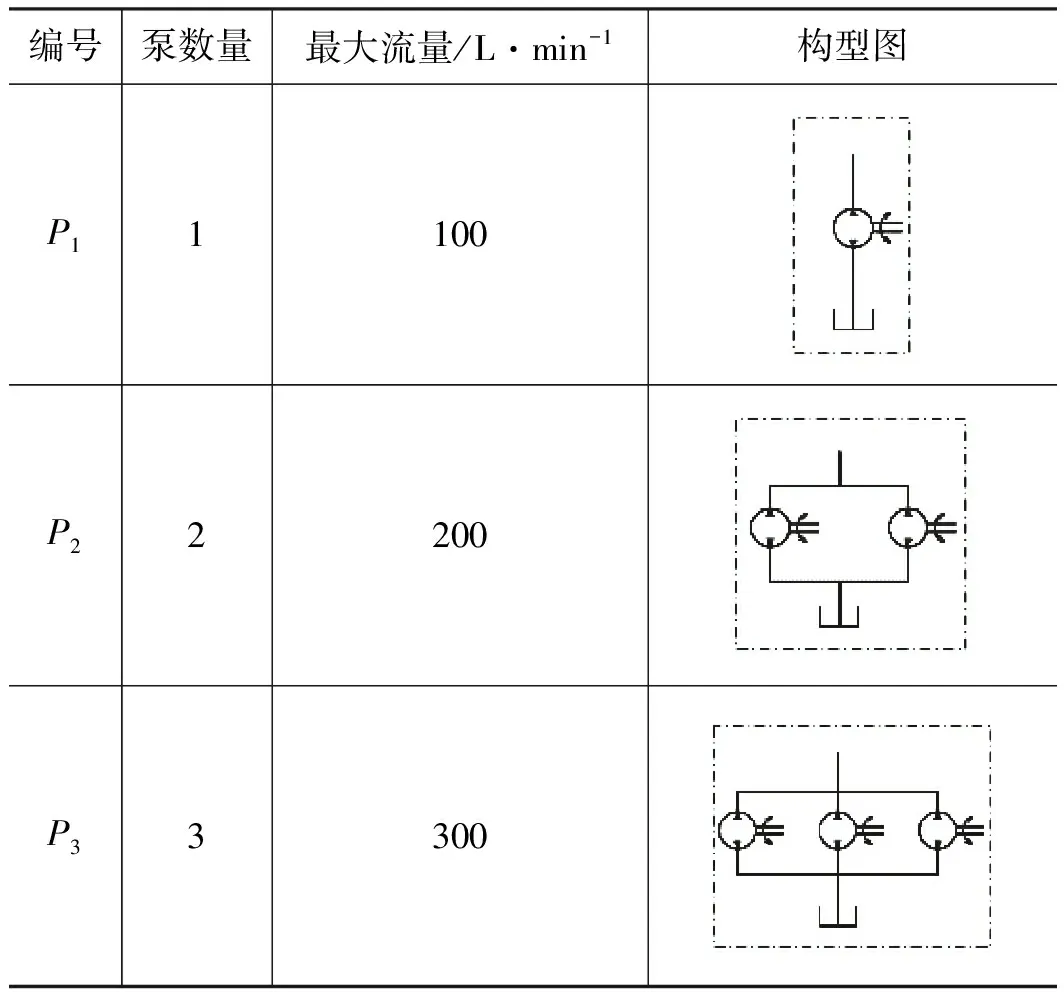
表1 泵的构型
蓄能器在主被动复合式升沉补偿系统中起到平衡静态负载的作用。蓄能器在不同构型的差别为冗余数量的差别,如表2所示。根据AMESim仿真结果,当2个被动补偿缸共同连接1个有效体积为20 L的蓄能器时,蓄能器的体积难以支撑6级海况时升沉补偿系统的工作要求,补偿效率会有明显的下降,因此,本研究分别考虑2个蓄能器、3个蓄能器和4个蓄能器,对应的蓄能器有效体积分别为40 L,60 L和80 L。
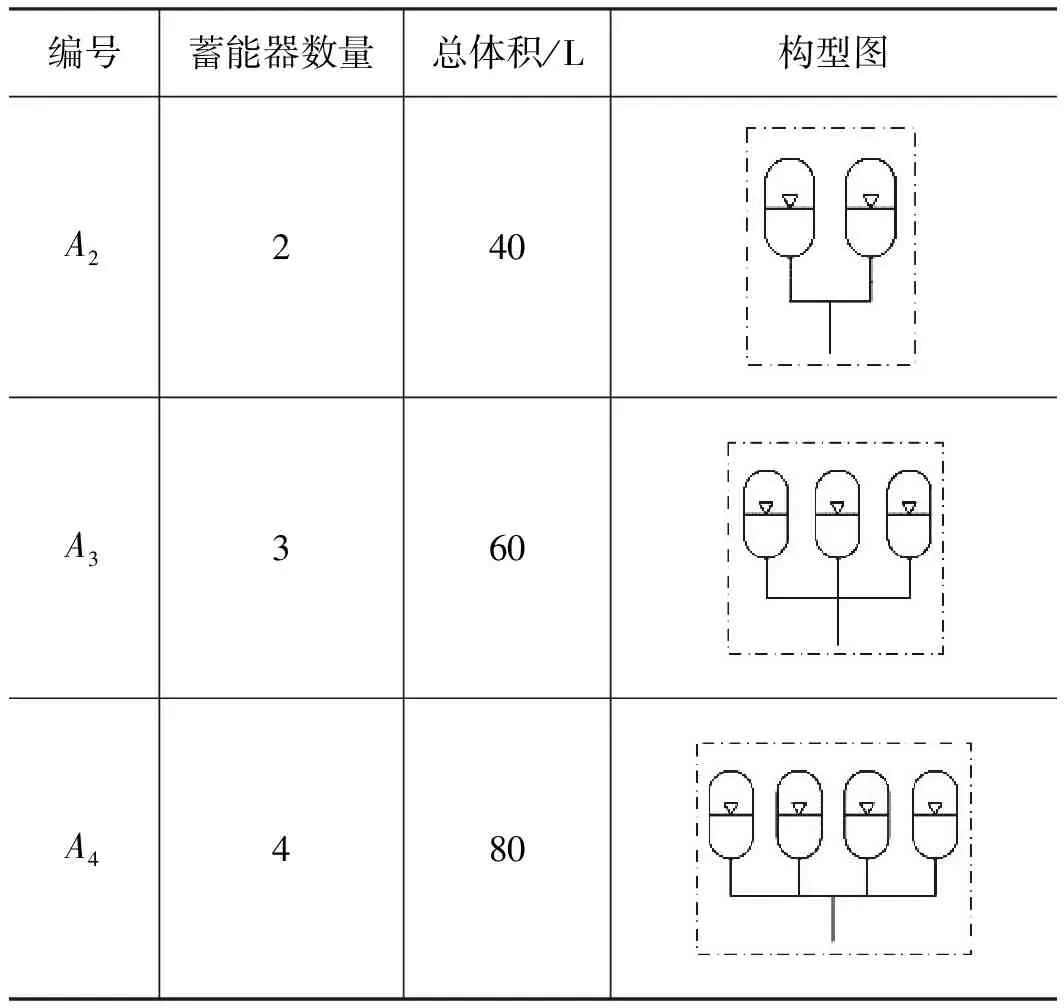
表2 蓄能器的构型
根据升沉补偿系统的设计要求,可确定决策变量为泵、蓄能器、补偿装置1和补偿装置2,表示成变量集合的形式为V={P,A,D1,D2}。其中P表示泵,其值域为P={P1,P2,P3};A表示蓄能器,其值域为A={A2,A3,A4};D1表示补偿装置1,其值域为D1={DC1,DC2,DC3};D2表示补偿装置2,其值域为D2={DC1,DC2,DC3}。
升沉补偿系统在配置构型时需要满足一定的约束条件,根据设计要求,补偿装置1和补偿装置2既可以采用相似冗余设计,也可采用非相似冗余设计。基于上述约束条件,共有54种升沉补偿系统构型组合满足约束条件。
2 升沉补偿系统目标函数评估
对于升沉补偿系统,一方面要考虑可靠性和补偿效率的提升,另一方面要考虑成本因素的限制。因此,可靠性R、成本C和补偿效率η成为升沉补偿系统多目标构型优化的3个目标函数,记为Z=[RCη]。不同构型的可靠性、成本和补偿效率会相互制约,以泵为例,多台泵的可靠性高于1台泵,同时对于恶劣海况的补偿效率也会提升,但是成本也会随之上升。
不同的工况影响着升沉补偿系统的工作模式,也影响着系统的目标函数,因此在对目标函数进行评估前,首先需要确定系统的工况。根据对海浪的分析结果可知,海浪能量集中在0.1 Hz左右,因此在多目标构型优化中,本研究采用频率为0.1 Hz的正弦波模拟海浪,浪高为2 m,对应出现概率最高的4级海况条件。
2.1 可靠性评估方法
可靠性是定量评估系统在规定的使用条件下,在规定的时间内,完成规定功能的能力。升沉补偿系统应用在恶劣的海洋工况下,为海洋作业提供安全稳定的支撑,其可靠性直接影响着海洋作业的安全性和稳定性。正因此,对于升沉补偿系统有着高可靠性的要求。此外,升沉补偿系统离岸工作的特点使其维护维修存在诸多不便之处,因此需要尽可能提高系统的可靠性,降低系统故障发生的概率。
可靠性框图法是一种常用的可靠性预计方法,这种方法是从可靠性角度出发研究系统与部件之间的逻辑图。升沉补偿系统整体的可靠性框图如图5所示,泵、蓄能器和补偿装置三者为串联关系,其中补偿装置中的补偿装置1和补偿装置2互为彼此的备份,为并联关系,因此系统整体的可靠性可以表示为:

图5 升沉补偿系统可靠性框图
R=RPRA[1-(1-RD1)(1-RD2)]
(1)
式中,RP——泵组的可靠性
RA——蓄能器组的可靠性
RD1,RD2——补偿装置1和补偿装置2的可靠性
在设计工况要求下,1台泵所能提供的流量满足升沉补偿系统正常工作的需求。因此,泵组是一个简单的并联系统,其可靠性可以表示为:
RP=1-(1-Rp)np
(2)
式中,Rp——单台泵的可靠性
np——泵的台数
由于主被动复合式升沉补偿系统正常工作至少需要2个蓄能器,因此蓄能器组是一个2/n的表决系统,其可靠性计算可由下式得到:
(3)
式中,na——蓄能器的个数,构型A2,A3,A4分别为2,3,4
i——构型i
Ra——单个蓄能器的可靠性
补偿装置构型1,2,3的可靠性框图如图6a~图6c所示,由此可计算3种构型的可靠性。
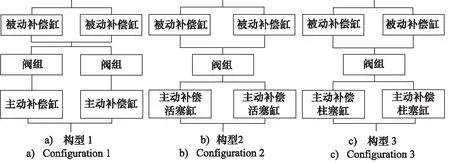
图6 补偿装置可靠性框图
由于部件和系统的可靠性是随时间变化的,因此本研究选取500 h时不同构型的可靠性作为评估的目标函数。表3列出了各个构型在500 h时的可靠性,结合式(1)~式(3),可计算出不同构型的升沉补偿系统可靠性。
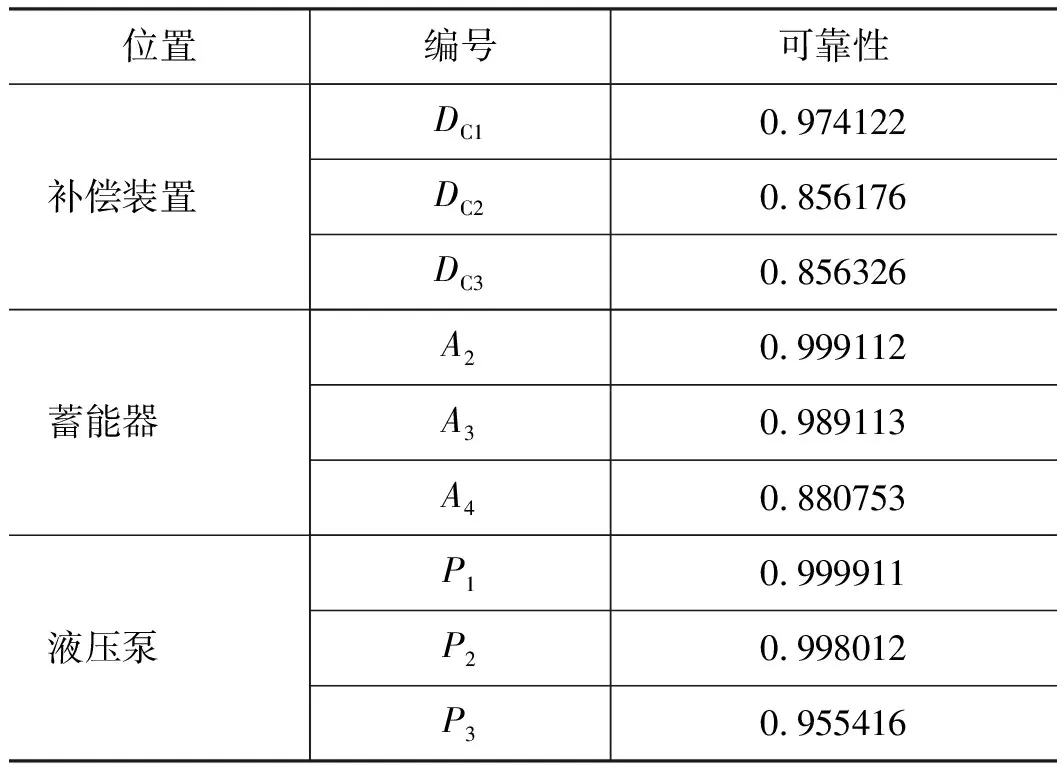
表3 500 h时各个构型可靠性
2.2 成本评估方法
在不考虑成本因素时,升沉补偿系统可以通过增加冗余来提高可靠性,防止补偿效率下降。对于实际的海洋作业装备,成本问题是升沉补偿系统开发及后续维护的一个重要约束指标,经济性也影响着商业化的发展。同时,成本因素也是限制升沉补偿系统可靠性和补偿效率提升的主要因素之一。因此,本研究考虑成本为升沉补偿系统多目标构型优化的一个目标函数。
升沉补偿系统的成本C可以表示为:
C=CP+CA+CD1+CD2
(4)
式中,CP——泵组的采购成本
CA——蓄能器组的采购成本
CD1,CD2——补偿装置1和补偿装置2的采购成本
表4列出了各个构型的采购成本,结合式(4),可计算出不同构型的升沉补偿系统的成本。
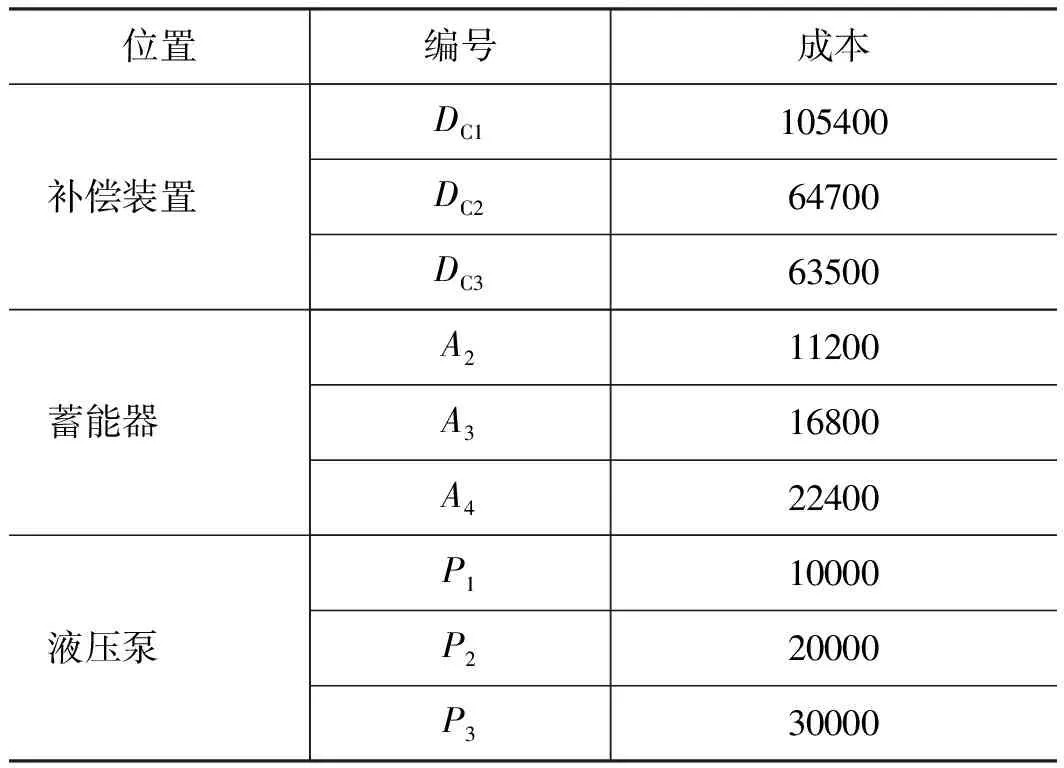
表4 各个构型成本
2.3 补偿效率评估方法
升沉补偿系统设计的初衷就是为了补偿海洋作业时母船受海浪影响造成的升沉运动,因此补偿效率是升沉补偿系统的关键技术指标。本研究利用AMESim软件对于不同构型的升沉补偿系统进行仿真,评估其补偿效率。
不同构型的补偿装置的补偿效率定义为峰值抑制率,即:
(5)
式中,ηCi——补偿装置构型i的补偿效率(i=1, 2, 3)
Δh0——补偿前负载运动的峰值
Δh——补偿后负载运动的峰值
在单纯的被动式升沉补偿系统中,蓄能器体积直接影响升沉补偿系统刚度,对补偿效率有明显的影响。而在主被动复合式升沉补偿系统中,蓄能器仅在被动补偿时起到平衡静态负载的作用;当控制阀组驱动主动补偿缸运动时,只要蓄能器提供的流量满足被动补偿缸的流量需求即可。通过AMESim仿真分析验证,当同一构型的补偿装置在分别连接不同有效体积的蓄能器时,补偿装置的补偿效果存在一定的差别,差别大概在毫米级别,相对较小。此外,根据AMESim仿真结果,1台泵所提供的流量可以满足设计工况的要求。基于以上两点,不同构型的升沉补偿系统的补偿效率几乎不受泵的构型和蓄能器的参数影响,可以通过直接分析不同构型补偿装置的补偿效率来确定整个系统的补偿效率。
本研究设计的升沉补偿系统具有2套补偿装置,因此,将不同构型的升沉补偿系统的补偿效率定义为2套补偿装置补偿效率之和,即:
η=η1+η2
(6)
式中,η1和η2分别为补偿装置1和补偿装置2的补偿效率。
通过AMESim仿真,补偿装置构型1,2,3对于模拟海浪的补偿效果分别如图7所示,补偿效率分别为94.0%,88.5%和89.6%。
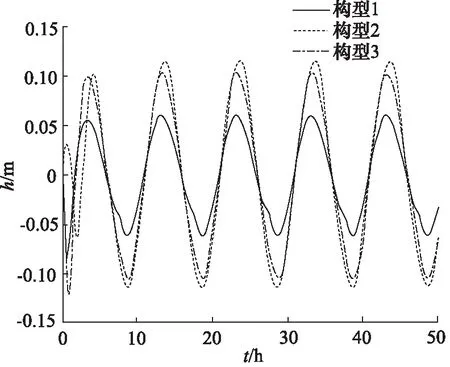
图7 不同补偿装置构型补偿效率
3 升沉补偿系统多目标构型优化
3.1 非支配排序
在确定不同构型的升沉补偿系统多个目标函数后,应用多目标优化算法对不同构型进行评估,其流程图如图8所示。升沉补偿系统评估为离散评估问题,同时存在多个评价指标,选用离散非支配排序,得到Pareto前沿解集,对构型数量的进一步降级。
支配定义为:任意决策向量x1和x2,对于全部的目标函数都有fi(x1)不比fi(x2)差,且至少存在一个目标函数满足fj(x1)比fj(x2)好,则认为x1支配x2,x1是非支配的,x2是受支配的。如果某个解x不受其他解的支配,则称这个解x为Pareto最优解。由Pareto最优解构成的集合成为Pareto前沿解集。如图9所示,构型1支配构型4,构型2支配构型5,构型3支配构型6,构型1,2,3组成Pareto前沿解集,并且相互之间没有支配关系。
本研究以可靠性、成本和补偿效率作为升沉补偿系统多目标构型优化的目标函数,希望在成本最小化的同时,可靠性和补偿效率尽可能的高,因此,升沉补偿系统的多目标优化问题可表述为:
f={maxfR(i),minfC(i),maxfη(i)}
(7)
式中,fR(i)——升沉补偿系统的可靠性
fC(i)——升沉补偿系统的成本
fη(i)——升沉补偿系统的补偿效率
本研究采用非支配排序的方法求解Pareto前沿解集,在这种排序方法中,计算复杂度仅为O(MN2)。对所有构型Y进行分层,根据目标函数,计算所有构型Y中支配构型i的数量ni,同时将被构型i所支配的所有构型纳入集合Si中。快速非劣分层的步骤为:
(1)在所有构型Y中查找所有ni=0的构型,并保存到集合F1中;
(2)当前集合F1中存在的每个构型i,被其支配的个体的集合为Si,对Si中每个构型l进行遍历,然后执行nl=nl-1,如果满足条件nl=0,那么在集合H中保存l;
(3)将F1中的构型视为首个非支配层个体,并把H视为当前集合,重复上述的步骤,将所有构型分层。
应用非支配排序将升沉补偿系统的所有构型进行分层,获得升沉补偿系统的Pareto前沿解集,如图10中圆圈所示。
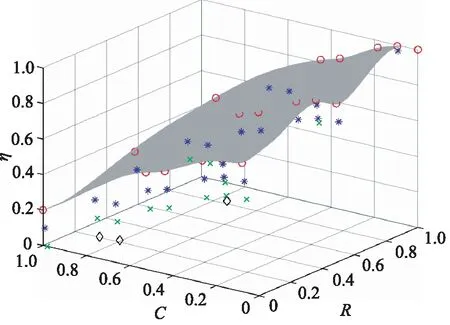
图10 升沉补偿系统Pareto前沿解集
3.2 层次分析法
多目标优化得到的不是一个最优解,而是一组多目标相互折中的Pareto前沿解集。优化结果有多个可行解时,如何在这些可行的目标解中,寻找一个最好的优化结果是进一步提高升沉补偿系统构型优化设计的关键问题。应用层次分析法把复杂的决策系统层次化,通过逐层比较多种关联因素的重要性,为分析、决策提供定量的依据。其基本原理是根据问题的性质和所要达到的总目标,将其分解为不同的组成因素,依照因素间的隶属关系和相互影响,按不同层次聚集组合后形成的一个多层次分析结构模型,利用人的经验对决策方案优劣进行排序,确定每一层的全部因素相对重要的权重值,进而提出最优方案。
图11为层次分析法结构图,将得到升沉补偿系统最优构型的目标设置为目的层,将补偿效率、可靠性、成本评价指标作为准则层,经过Pareto优化集合的各个构型方案作为方案层。在建立升沉补偿系统构型优化层次分析法模型以后,根据设计经验和专家意见,引入判断矩阵,计算每个构型的得分,以此确定升沉补偿系统的最优构型。
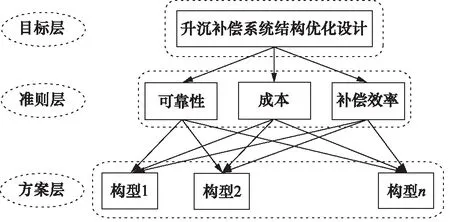
图11 层次分析法的结构图
根据升沉补偿系统各个目标函数之间的相对重要性,构建目标函数之间的判断矩阵B=(bij),bij表示第i个目标函数相对第j个目标函数的重要程度,bij的取值可根据表5确定。在判断矩阵B中bij=1/bji,且对角线元素bii=0。

表5 判断矩阵相对重要程度
在根据设计经验和专家意见构造判断矩阵B后,需要对判断矩阵B进行一致性检验,目的是为了避免各个目标函数之间的矛盾关系。例如,当目标函数1的重要程度大于目标函数2,且目标函数2的重要程度大于目标函数3,则目标函数1的重要程度必然大于目标函数3,不可能存在目标函数3的重要程度大于目标函数1的情况。矩阵的一致性通常按照式(8)进行判断:
(8)
式中,K——判断矩阵一致性指标系数
λmax——判断矩阵的最大特征根
n——判断矩阵的阶数,本研究有3个目标函数,所以n取值为3
Ka——判断矩阵的平均随机一致性指标系数,当n为3时,Ka取值为0.58
ζ——判断矩阵的随机一致性比率,若ζ小于0.1,则说明判断矩阵满足一致性要求;若判断矩阵B不满足一致性要求,则需要调整判断矩阵的元素取值,并重新进行一致性检验
本研究根据升沉补偿系统目标函数之间的相对重要性给出了判断矩阵B,考虑的目标函数为可靠性、成本和补偿效率。判断矩阵B为:
(9)
经检验,该矩阵满足一致性要求。
根据判断矩阵可以计算各个目标函数的相对权重,首先计算判断矩阵最大特征值λmax对应的特征向量w,将w归一化得到的归一化向量W即为各个目标函数的权重,本研究中可靠性、成本和补偿效率的权值系数W为:
(10)
因此每个构型的得分为:
S=ZW
(11)
得分最高的即为最佳构型,根据层次分析法获得的升沉补偿系统最优构型集合为Vm={P2,A4,DC1,DC3}。
4 结论
本研究提出了一种升沉补偿系统构型的多目标优化方法。首先,根据工作原理分析和设计要求,液压泵、蓄能器和补偿装置被确定为决策变量;然后,根据约束条件确定符合条件的升沉补偿系统构型解集,分别给出了可靠性、成本和补偿效率的评估方法;再利用非支配排序获得升沉补偿系统的Pareto前沿,进一步缩小构型范围,在此基础上构造判断矩阵、利用层次分析法综合评定Pareto前沿中每个构型的分数,最终获得了升沉补偿系统的最优构型。后续工作将关注拓展升沉补偿系统的构型空间,同时对实际系统的可靠性、成本和补偿效率进行更加全面和准确的评估,以进一步寻找最优构型。

