相对交连续半格及其等价刻画
陈必琴,姜广浩①
(淮北师范大学 数学科学学院,安徽 淮北 235000)
0 引言
Domain理论为计算机程序设计语言的指称语义学奠定数学基础,属于格论、拓扑学、范畴论及理论计算机科学为基础的交叉学科,而连续Domain是Domain理论中的重要研究对象[1-7].而作为Domain理论的重要理论特殊元理论,是众多学者研究的热门话题.文献[8-9]对偏序集上的弱理想的研究取得丰富的成果,文献[10-11]对偏序集上的局部极大理想和滤子极大理想的探究也取得不错成绩.近年来,这方面的研究得到一些好的结果[11-15].文献[16-17]将经典概念定向集推广为一致集,引入并探讨一致连续偏序集.文献[18]利用相对的思想引入相对定向集的概念,探讨相对连续偏序集及其性质[18-20].作为Domain理论中交连续半格这一经典概念的自然推广,本文首先引入相对辅助关系的概念,研究其在给定的集合T中的一些性质;然后利用相对辅助关系定义相对逼近辅助关系的概念.此外给出相对交连续半格的概念,并得到其若干内部刻画.最后探讨相对连续Domain及其若干拓扑性质,并研究相对连续半格与相对交连续半格之间的关系.
1 预备知识
设P为偏序集,记↓X={y∈P:∃x∈X,y≤x},↑X={y∈P:∃x∈X,x≤y},↓x=↓{x},↑x=↑{x}.X⊆P,称X为下集当且仅当X=↓X;X为上集当且仅当X=↑X.设X⊆P,X≠∅,若∀x,y∈X,∃z∈X使得x,y≤z,则称X是P的定向子集.设X⊆P,X为理想当且仅当X既是下集又是定向集.记P所有的理想构成的集合为Idl(P).若对于任意定向子集D,supD存在且supD∈D,则称P是定向完备的.简记为dcpo.
定义1[2]若偏序集L上的二元关系"≺"满足:
(1)x≺y⇒x≤y.
(2)u≤x≺y≤z⇒u≺z.
(3)若最小元0存在⇒0≺x.
称"≺"为辅助关系,全体"≺"记为Aux(L).
定义2[18]设L是偏序集,S,T⊆L,S≠∅,若∀x,y∈S,存在t∈T,使得x≤t,y≤t,则称S为偏序集L上相对于T的定向集.当T明了时,简称S为相对定向集.记U(T)={S:S为相对于T的定向集}.
定义3[18]设L是偏序集,I,T⊆L,I≠∅,T≠∅,若I相对于T定向且I为下集,则称I是偏序集L上相对于T的理想,当T明确给定时,简称I为相对理想.记RIdl(T)={I:I为相对于T的理想}.
定义4[18]设L是偏序集,T⊆L,T≠∅,若任意相对于T的定向集S,L都有最小上界supS,则称L为相对于T的定向完备集;当T明了时,则称L为相对定向完备集,记为RDCPO(T).
定义5[18]设L是偏序集,T⊆L,T≠∅,L为相对于T的定向完备集,∀x,y∈L,若对于任意相对于T的定向集D,当y≤supD时,∃s∈D,使x≤s,则称x在L上相对于T双小于y,当T明确给定时,记为x<<T y.若x<<T x成立,则称x为L上相对于T的紧元,当T明确给定时,称为x为相对紧元.记⇑T x={u:x<<Tu},⇓T x={v:v<<T x}.
定义6[18]设L是偏序集,T⊆L,T≠∅,U⊆T,若U满足:
(1)U=↑TU={z∈T:∃x∈U,x≤z};
(2)对于L中的任意相对于T的定向集D,当supD∈U时,∃d∈D使得d∈U,则称U是L的相对T的Scott开集,当T明确给定时,简称为相对Scott开集.令σT(L)={U⊆L:U为L的相对于T的scott开集},则σT(L)为T的一个拓扑,称它为L上相对于T的Scott拓扑,当T明确给定时,简称为相对scott拓扑.
2 相对交连续定向完备半格
首先来定义相对辅助关系,再依赖此定义展开其他研究.
定义7设L是偏序集,T⊆L,T≠∅,L为相对于T的定向完备集,对于任意u,x,y,z∈T,若L上的二元关系"≺T"满足:
(1)x≺T y⇒x≤y;
(2)u≤x≺T y≤z⇒u≺T z;
(3)若L上有最小元0存在⇒0≺T x.
称"≺T"为相对辅助关系,全体"≺T"记为RAux(L).
命题1二元关系"≺T"满足下列两条性质:
(1)反对称性:∀a,b∈L,若a≺Tb,b≺Ta,有a≤b,b≤a,即a=b;
(2)传递性:∀a,b,c∈L,若a≺Tb,b≺Tc,有a≤b,b≺Tc,即a≺Tc.
例1设L是连续偏序集,T⊆L,T≠∅,L为相对于T的定向完备集,则L上的"≤T","<<T"为相对辅助关系.
定义8在dcpo L中,设T⊆L,T≠∅,L为相对于T的定向完备集,L上的相对辅助关系"≺T"称为相对逼近关系当且仅当集合{u∈T:u≺T x}=s≺T(x)是定向的,且∀x∈L,x=sup{u∈T:u≺T x}=sups≺T(x),所有的相对逼近辅助关系记为RApp(L).在偏序集中"≤T"是相对逼近辅助关系,Domain中"<<T"为相对逼近辅助关系.
命题2在dcpo L中,设T⊆L,T≠∅,L为相对于T的定向完备集,"≺T"为L上的辅助关系,则下列条件等价:
(1)"≺T"为相对逼近的;
(2)∀x,y∈L,若x■y,则∃z≺T x使z■y.
证明(1)⇒(2)反证法:若∀z≺T x,有z≤y,则z∈s≺T(x),从而sups≺T(x)≤y,由(1)x≤y,矛盾.
(2)⇒(1)∀y∈L,显然sups≺T(y)≤y.设sups≺T(y)=x,若y■x,由(2)知,∃t≺T y,t■x,矛盾.故y≤x,即y=sups≺T(y)=sup{u:u≺T y},故"≺T"是相对逼近的.
定义9设L是定向完备半格,若∀x∈L,T,D⊆L,D≠∅,D为L上相对于T的定向集,满足xsupD=supxD,则称L是相对交连续的半格.
下面给出相对交连续定向完备半格的若干等价刻画.
定理1在定向完备半格L中,设T⊆L,T≠∅,L为相对于T的定向完备集,则下列条件等价:
(1)相对理想的并映射I→supI:RIdl→L是一个并半格同态;
(2)对于相对理想I1,I2,有( s upI1)( s upI2)=supI1I2;
(3)对于相对定向集D1,D2,有( s upD1)(s upD2)=supD1D2;
(4)L是相对交连续的;
(5)∀相对定向集D和∀x≤supD,有x≤supxD;
(6)交运算(x,y)→xy:L×L→L保相对定向并.
证明(1)⇒(2)∀I1,I2∈RIdl,由(1)的并映射同态,有( s upI1)∧( s upI2)=sup(I1∧I2)=sup(I1I2).
(2)⇒(1)∀I1,I2∈RIdl,( s upI1)∧( s upI2)=sup(I1∧I2),即并映射同态.
(2)⇒(3)∀两个相对定向集D1,D2,需证( s upD1)(s upD2)=sup(D1D2),对D1,D2同时取下集↓D1,↓D2,
此 时↓D1,↓D2为 相 对 理 想,由(2)得,( s up↓D1)(s up↓D2)=sup(↓D1↓D2),下 证sup(↓D1↓D2)=sup(D1D2).
一 方 面,D1⊆↓D1,D2⊆↓D2,故D1D2⊆↓D1↓D2,sup(D1D2)≤sup(↓D1↓D2).令c=sup(D1D2),e=sup(↓D1↓D2),则c≤e;∀f∈↓D1↓D2,则∃d1∈D1,d2∈D2,使f≤d1,f≤d2,有f≤d1d2≤supD1D2=c,故c为↓D1↓D2的一个上界,又e为↓D1↓D2的上确界,即最小上界,故e≤c,即e=c.
另一方面,因为自身性和传递性,D1和↓D1有相同的上界.设a=supD1,b=sup↓D1,由D1⊆↓D1,有supD1≤sup↓D1,即a≤b.又∀d∈↓D1,∃d1∈D1,使d≤d1≤supD1=a,即d≤a,从而a为↓D1的上界,又b为↓D1的最小上界,故b≤a,即a=b,则supD1=sup↓D1.同理supD2=sup↓D2.
综上,( s upD1)( s upD2)=sup(D1D2)成立.
(3)⇒(2)因为相对理想为相对定向集,故(2)成立.
(3)⇒(4)令D1={x},D2=D,则( s upD1)( s upD2)=xsupD,supD1D2=supxD,从而xsupD=supxD,故(4)成立.
(4)⇒(5)由(4),L为相对交连续,D为相对定向集,满足xsupD=supxD.∀相对定向集D,若x≤supD,两边同时取交,x∧x≤x∧supD,即x≤xsupD.
(5)⇒(6)设D⊆T,D⊆L×L是相对于T的定向集,且集Dn=πnD,n=1,2,…,那么D⊆D1×D2.另一方面,(d,e)∈D1×D2,∃x,y∈L,(d,y),(x,e)∈D,因D相对定向,(d*,e*)∈T,有(d*,e*)∈↓D,由(d,e)≤(d*,e*),有(d,e)∈↓D,从而D1×D2⊆↓D.
设m:L×L→L,m(x,y)=xy,则
m(D)⊆m(D1×D2)=D1D2⊆m(↓D)⊆↓m(D),
故supm(D)≤supD1D2≤sup↓m(D)=supm(D),即supm(D)=supD1D2.
令d1=supD1,d2=supD2,则(
d1,d2)=supD.
下证d1d2=supD1D2,∀x∈D1,有xd2≤supD2,因此xd2=supxd2D2=supxD2,又d1d2≤supD1,即d1d2=supd1d2D=supD1d2,那么

即( s upD1)( s upD2)=supD1D2,则∧supD=sup∧D,即m(s upD)=supm(D).
(6)⇒(3)显然.
定义10在dcpo L中,设T⊆L,T≠∅,L为相对于T的定向完备集,∀I∈RIdL,定义
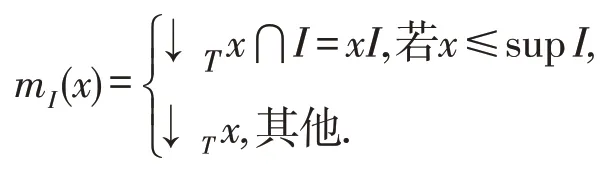
命题3在相对交连续半格L中,∀I∈RIdL,所有属于函数mI的关系都是相对逼近的.
证 明设x∈L,若x≤supI,则 由 定 理1有,supmI(x)=supxI=xsupI=x;若x■supI,则supmI(x)=sup↓T x=x.
定理2在定向完备半格L中,设T⊆L,T≠∅,L为相对于T的定向完备集,所有的相对逼近辅助关系包含"<<T"关系.若L为相对交连续半格,则"<<T"⇔相对逼近辅助关系的交,即⇓T x=s<<T(x)=⋂{s≺T(x):≺T∈RApp(L)}.
证明设y<<T x,"<<T"是相对逼近辅助关系,有{u∈L:u≺T x}是相对于T的定向集,且上确界为x,则∃u,有y≤u≺T x,因此y≺T x,即<<T⊆≺T.
另一方面,若L为相对交连续半格,由命题3有⇓T x=⋂{mI(x):I∈RIdL}⊇⋂{s≺T:≺T∈RAPP(L)}.
定义11L为偏序集,设T⊆L,T≠∅,L为相对于T的定向完备集,若L上的相对逼近辅助关系满足:∀x,z∈L,x≺T z且x≠z⇒∃y,有x≺T y≺T z且x≠y,则"≺T"具有强插值性质;∀x,z∈L,x≺T z⇒∃y,x≺T y≺T z,则"≺T"具有插值性质.
定理3在定向完备半格L中,设T⊆L,T≠∅,L为相对于T的定向完备集,若L上的相对逼近辅助关系满足:∀x,z∈L,x≺T z且x≠z⇒∃y,x≤y≺T z且x≠y.
证明∀z∈L,z=sup{u∈L:u≺T z}=sups≺T(z),有u≺T z,u■x.当s≺T(z)={u∈L:u≺T z}是相对定向时,由u■x,x≠y,则∃{x,u}的一个上界y,有y≺T z.
定理4在定向完备半格L中,设T⊆L,T≠∅,L为相对于T的定向完备集,若"≺T"为L上的相对逼近辅助关系,则下列条件成立:
(1)若x<<T z,x≠z且z≤supD,D为相对定向集,则∀d∈D,x≺Td,x≠d;
(2)若x<<T z且x≠z,则∃y,使得x≺T y≺T z,且x≠y.
证明(1)任取D∈U(T),因L为相对于T的定向完备集,故supD存在,且满足z≤supD.
令I=⋃{s≺T(d):d∈D},且supI=sup{s ups≺T(d):d∈D}=supD,故z≤supI,又x<<T z,则x∈I.即∃d∈D,有x≺Td.
(2)令D=s≺T(z)={y∈L:y≺T z},z=sups≺T(z)=supD.若x<<T z且x≠z,由(1),∃y∈D,有x≺T y且y≠x,则x≺T y≺T z.
由定理4可得如下结论.
推论1在相对连续Domain中,相对way below关系满足强插值性质.
3 相对连续Domain
定义12设L为偏序集,T⊆L,T≠∅,且L为相对于T的定向完备集,若∀x∈L,x=sup↑⇓T x,则称L为相对于T的连续偏序集.当T明了时,简称L是相对连续偏序集.若L为dcpo,则称L为相对于T的Domain.若相对DomainL是半格,则称L为相对连续半格.↑⇓T表示相对定向双下集.
定理5相对连续半格是相对交连续半格.
证明设L是相对连续半格,T⊆L,T≠∅,D是相对于T的定向集,且x≤supD,由定理1中(5),要证x≤supxD,即证⇓T x⊆⇓supxD⊆↓supxD.事实上,∀y∈⇓T x,有y<<T x,从而y≤x.又∃z∈D使y≤z,从而y≤xz∈xD,则y≤supxD,即y∈↓supxD,综上⇓T x⊆↓supxD,故x≤supxD.
定理6在dcpo L中,设T⊆L,T≠∅,L为相对于T的定向完备集,下列条件等价:
(1)L相对连续Domain;
(2)<<T是最小的相对逼近辅助关系;
(3)L上有最小的相对逼近辅助关系.
证明(1)⇒(2)由L是相对连续Domain知,"<<T"是相对逼近辅助序,所以⇓T x是相对理想.又由{s≺T(x):≺T是相对逼近的}⊆{I∈RIdL:x≤supI},所 以⋂{s≺T(x):≺T是相对逼近的}⊇⋂{I∈RIdL:x≤supI}=⇓T x.又 因"<<T"是 相 对 逼 近 的,则⇓T x∈{s≺T(x):≺T是相对逼近的},所 以⇓T x=⋂{s≺T(x):≺T是相对逼近的}.
(2)⇒(3)显然.
(3)⇒(1)若L有最小的相对逼近辅助序M,下证∀x∈L,M=⇓T x.事实上,M⊆⋂{I∈RIdL:x≤supI}=⇓T x⊆M,从而有M=↑⇓T x,所以L是相对连续Domain.
下面给出相对连续Domain中Scott开集的若干性质.
定理7若L是相对连续Domain,T⊆L,T≠∅,⇑T x⊆T,则下列条件成立:
(1)∀x∈L,集合⇑T x是相对于T的Scott开集;
(2)若L是定向dcpo且y∈int(↑T x),则x<<T y.
证明(1)因⇑T x是L上相对于T的上集,只需证定义6中的(2).设D为相对于T的定向集,且supD∈⇑T x,则x<<TsupD.又L为 相 对 连 续Domain,∃d∈D,使 得x<<Td,即d∈⇑T x,故D⋂⇑T x≠∅,⇑T x为相对Scott开集.
(2)若L是dcpo且y∈int(↑T x),设D是L上相对于T的定向集,且y≤supD,故supD∈↑y⊆int(↑T x),D⋂int(↑T x)≠∅.从而∃d∈D,有d∈int(↑T x)⊆↑T x,有x≤Td,即x≤d,故x<<T y.
定理8设L是相对连续Domain,则下列条件成立:
(1)上集U是相对T的Scott开集⇔∀x∈U,∃u∈U,使得u<<T x;
(2){⇑Tu,u∈L}构成σT(L)的一个基;
(3)在σT(L)中,有int(↑T x)=⇑T x.
证明(1)⇒设T⊆L,T≠∅,上集U是相对于T的Scott开集且x∈U,又L为相对连续Domain,有x=sup↑⇓T x,故sup↑⇓T x∈U,即⇓T x⋂U≠∅.从而∃u∈U,有u∈⇓T x,即u<<T x.
⇐若∀x∈U,∃u∈U,使得u<<T x,即x∈⇑Tu.因U⊆⋃{⇑Tu:u∈U}⊆U,即U=⋃{⇑Tu:u∈U},由定理7(1)知,⇑T x是Scott开的,即U为相对于T的scott开集.
(2)由(1)显然.
(3)设T⊆L,T≠∅,因⇑T x⊆↑T x,有⇑T x⊆int(↑T x).反之,由定理7(2)知,int(↑T x)⊆⇑T x,故⇑T x=int(↑T x).

