一类非线性微分方程三阶三点边值问题三个正解的存在性
武晨①
(江苏联合职业技术学院 南京分院,江苏 南京 210019)
0 引言
三阶微分方程边值问题来源于应用数学及物理学领域中,例如弯曲梁的挠度、电磁波和重力驱动流等方面.正因为其强大的理论价值和应用背景引起众多学者的关注.通过对三阶微分方程所对应的不同边值条件的研究也得到一系列重要的研究成果[1-20].例如文献[4]研究如下的一个三阶边值问题:

正解的存在性.作者通过构造相应的Green函数,在证明该Green函数的一系列性质基础之上,应用锥拉伸和压缩不动点定理得到上述边值问题 至少一个正解的存在性结果;文献[13]利用迭代的方法得到如下三阶边值问题:

在本文中,假设f∈C([0,1]×[0,+∞)→[0,+∞)).
1 相关引理和定义
令E=C[0,1],赋予范数,显然E为Banach空间.设P为E中的锥,φ为P中的一个非负连续泛函,若a,b,r>0是三个给定的常数,记:

引理1.1[5,9](Leggett-Williams不动点定理)假设0<d<a<b≤c,→是一个全连续算子,φ为P上的一个非负连续泛函,对任意u∈,使得φ(u)≤‖‖u成立,且有:
(i){u∈P(φ,a,b):φ(u)>a}≠∅,且当u∈P(φ,a,b)时,φ(Tu)>a;
(ii)当u∈时,‖‖Tu<d;
(iii)当u∈P(φ,a,c)且‖‖Tu>b时,恒有φ(Tu)>a成立.则T在中至少存在3个不动点u1,u2,u3满足‖‖u1<d,a<φ(u2),‖‖u3>d,φ(u3)<a.
引理1.2[6,8]设,则对任意给定的h(t)∈C[0,1],边值问题:

有唯一解:

其中

引理1.3[6,8]对于任意(t,s)∈[0,1]×[0,1],G(t,s),G1(t,s)有如下性质:

引理1.4[8]令0<τ<1,边值问题(3)有唯一解u(t)≥0,且满足

显然算子T的不动点即为边值问题(2)的解.
引理1.5[6,8]算子T:P→P是全连续的.
2 主要结果
定理2.1如果存在常数a,c,d,其中,且满足下述条件:

则边值问题(2)至少存在3个正解u1(t),u2(t),u3(t),且满足
证明定义锥P上的一个非负连续泛函.显然,对于任意的u∈P,都有φ(u)≤‖‖u成立.
接下来,将逐步验证Leggett-Williams不动点定理的条件成立.
首先,证明存在一个常数c,使得当0≤u<c时,有,则由引理1.2、1.3和式(7)可知:


由引理1.3和式(6)的定义可知:
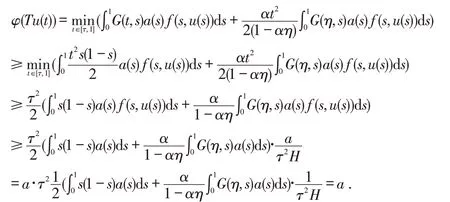

从而有‖‖Tu<d成立.
最后,证明若当u∈P(φ,a,c)且时,恒有φ(Tu)>a成立.因为u∈P(φ,a,c)且,从而根据引理1.3可知:

从而


