基于截痕法和遗传算法的FAST主动反射面形状调节模型研究
庞登浩,胡帆汛,李哲楷,连 横①
(安徽大学 互联网学院,安徽 合肥 230000)
0 引言
“中国天眼”500 m口径球面射电望远镜FAST工程,是中国乃至世界天文领域的重大科技基础设施项目.FAST索网主动反射面结构由2 226个主索节点、6 525根节点间连接主索以及4 300块反射面板构成.每个主索节点连接一根下拉索,下拉索下端与固定在地表的促动器连接,通过促动器顶端的伸缩,可控制主索节点的移动变位,但连接主索节点与促动器顶端的下拉索长度保持不变.主动反射面系统采用整体索网张拉设计,当位移距离和实际距离不相同时,控制促动器在径向上运动,使得索网移动并带动反射面运动到理想工作抛物面以汇聚目标天体电磁波,观测时抛物面会随着被观测物体移动,实现主动变位,使得反射面在照明区域内形成瞬时工作抛物面[1-2].主动反射面可以分为基准态和工作态2个状态[3],馈源舱的接收信号有效区域为直径1 m的中心圆盘.
文章研究目的在于求出主网反射面的理想抛物面,控制促动器带动主索节点的移动,使得主动反射面对理想抛物面的拟合达到最佳效果,从而使反射汇聚到馈源舱有效区域的电磁波数量最多.由于可知数据的局限性,本文做出如下3个假设:
假设1:假设面板上的小孔不影响对天体电磁波的反射.
假设2:假设促动器沿径向的伸缩导致的主索节点在纬向上的偏移可以忽略.
假设3:假设三角网格上的反射面板为球面.
1 模型及其原理
1.1 遗传算法与抛物线模型
遗传算法是一种通过模拟自然进化过程来搜索最优解的方法.遗传操作为选择、交叉和变异,关键步骤包括参数编码、设定初始群体、设计适应度函数、设计遗传操作及参数控制.
首先,以基准态球面的球心C为原点建立空间直角坐标系,将每一个主索节点投影到XOY平面上,可以得到其在XOY平面上的坐标M0i=(X0i,Y0i),(i=1,2,…,2 226),求到原点的距离,接着沿Z轴和d0i所在线为面做切割,得到一个二维平面,原点不变,以d0i所在线为现X轴,原Z轴为现Y轴,确定当前主索节点的新坐标即:
设抛物线顶点A与对应圆弧线最低点之间长度为h,抛物面的焦比为f.f、h为所需要控制的2个变量,使用遗传算法来搜索最优解[4].在此只需建立一个模型即可解决假定f不变以及f、h均可变的这2种情况,具体模型如下:
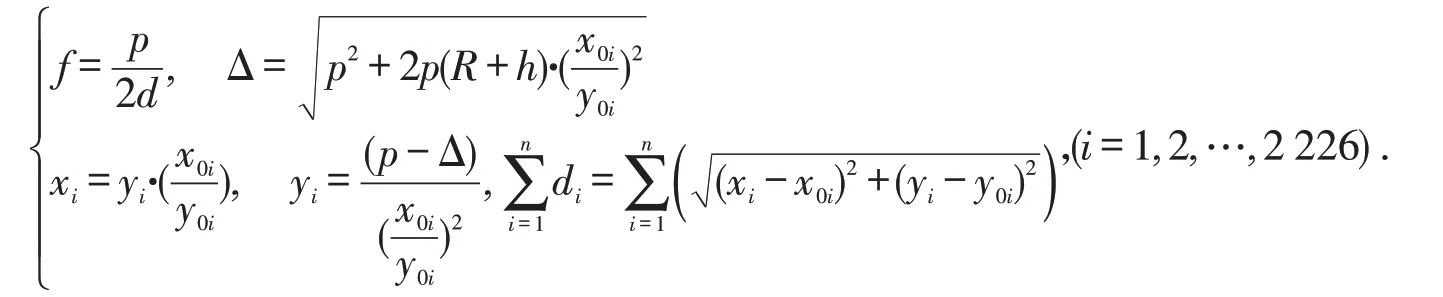
为进一步减少主动反射面的变形,减小工作抛物面弧长与基准球面的弧长差,提出对原模型的优化:在主索节点变化不超过0.07%的条件下,利用遗传算法对其进一步优化参数h.
设主索节点M′0i到抛物线顶点A的弧长为,积分求出,主索节点M′0i到500 m口径基准球面顶点O的弧长为
1.2 旋转矩阵转换法与天体方位变换模型
旋转矩阵[5-7]是指在乘以一个向量时,改变向量的方向但不改变其大小,并且保持手性的矩阵.利用主动旋转法将向量逆时针围绕旋转轴旋转,建立天体方位变换模型.
当目标天体不在馈源舱正上方时,将以目标天体与坐标原点C的连接线所在的轴S经2次矩阵旋转到原Z轴所在方向,再次建立新的空间直角坐标系.设S轴上任意一点R,α为天体的方位角,β为天体的仰角.点R先绕X轴旋转,再绕Z轴旋转α到Z轴.设点R的单位向量为E,c为常数,则有其中,绕X轴旋转的矩阵为:;绕Z轴旋转的矩阵为:,则有旋转矩阵T=Rx(β)·Rz(α),可得旋转后的最低节点为T·E,然后只需验证该向量的x,y是否为0,即可证明结果的正确性.由此就可将问题转化为“目标天体在基准球面正上方”的情况.
1.3 截痕法与主索节点调节模型
通过调节促动器可使主索节点从基准态球面移动到工作态抛物面上.采用截痕法,将三维空间内的位移问题转换到二维平面内,间接求出各主索节点变动后的空间坐标[8-9].
如图1(a)所示,Q(xo,yo,zo)在基准球面上,沿径向移动落到理想抛物面的上为Q′,Q′Q所在直线与点Q所在纵轴即z=zo形成平面,在此平面上过O点做z轴的垂线为降维变换后的横轴,记为x′轴,z轴为变换后的纵轴,记为y′轴,新坐标系如图1(b)所示.
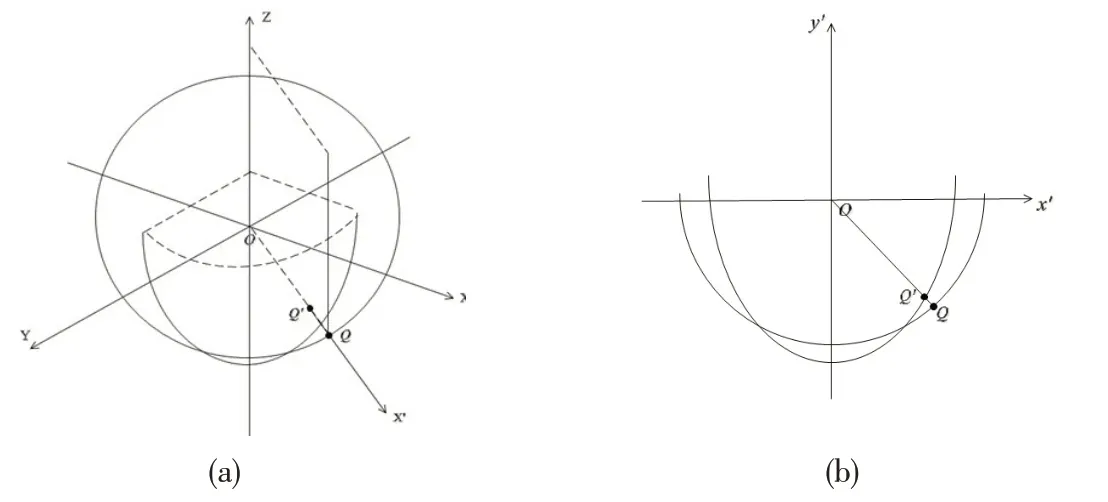
图1 截痕法降维图解
设在二维坐标系中,Q(x0,y0)(其中所在直线的方程为,联立抛物线方程可得:;以 及
2 研究结果
2.1 基准态下的理想抛物面
设抛物面口径为d=300 m,已知R=300 m,由此得.由文献[10-12]可知,焦点F位置的适当改变可使所得抛物线效果更佳.根据不同的限制条件,可给出2种优化f和h的方案.
对照组:f=0.466 0,h=0.焦点F确定,设f不变,抛物线顶点在对应圆弧线最低点,由此作为一个基础态来衡量后续方案的优劣.
方案一:f=0.466 0,h=0.60.假定f不变.在该情况下利用遗传算法[13]对h进行优化,在最优解下求得的理想抛物线方程为-x2+2×208.8y+1.681 0×105=0.
方案二:f=0.469 0,h=0.455 2.f、h均为变量.利用遗传算法对其进行优化,在最优解下求得理想抛物线方程为-x2+2×281.4y+1.690 96×105=0.
综合分析2种变形方案,可以看出方案二的效果明显优于方案一.因此,当f=0.469 0,h=0.455 2时,主动反射面的抛物线方程最理想,即基准态下的理想抛物面方程为:-x2-y2+2×281.4z+1.690 96×105=0.
2.2 工作态下的理想抛物面
在此以天体在α=36.795°,β=78.169°时为例求解.将所有主索节点代入天体方位变换模型,根据旋转结果找到最低节点的位置为R′=(0.000 0,0.000 0,6.090 8)(R′的X、Y轴的坐标结果均为10-16量级,因此完全可以将其视为0).证明旋转结果正确,故可根据基准态求得理想抛物线的方程为-x2+2×281.4y+1.690 96×105=0.
根据基准态下主索节点最低点的坐标(0,0,-300.4),经矩阵旋转可得最低节点的坐标M1(-49.319 4,-36.889 0,-294.018 7),抛物线顶点A1(-49.320 0,-36.889 4,-294.018 5).设某一主索节点坐标为Ni(xni,yni,zni),通过读取每个主索节点的坐标给Ni,然后将Ni乘以天体方位变换模型中的旋转矩阵,得到旋转后的主索节点位置坐标N′i(x′ni,y′ni,z′ni).通过约束条件Z′ni<150 3得出共有699个节点在300 m口径抛物面范围内.然后将所得每个主索节点的位置与理想抛物面的位置进行比较,主索节点的位置与对应理想抛物面上的点之间的欧氏距离即为促动器的伸缩量[14].
2.3 基准态反射球面与工作态馈源舱的接收比
馈源舱的接收比可转化为图2中1 m的直径长度与JK的长度之比,设馈源舱的接收比为P1,故在三角形中有:
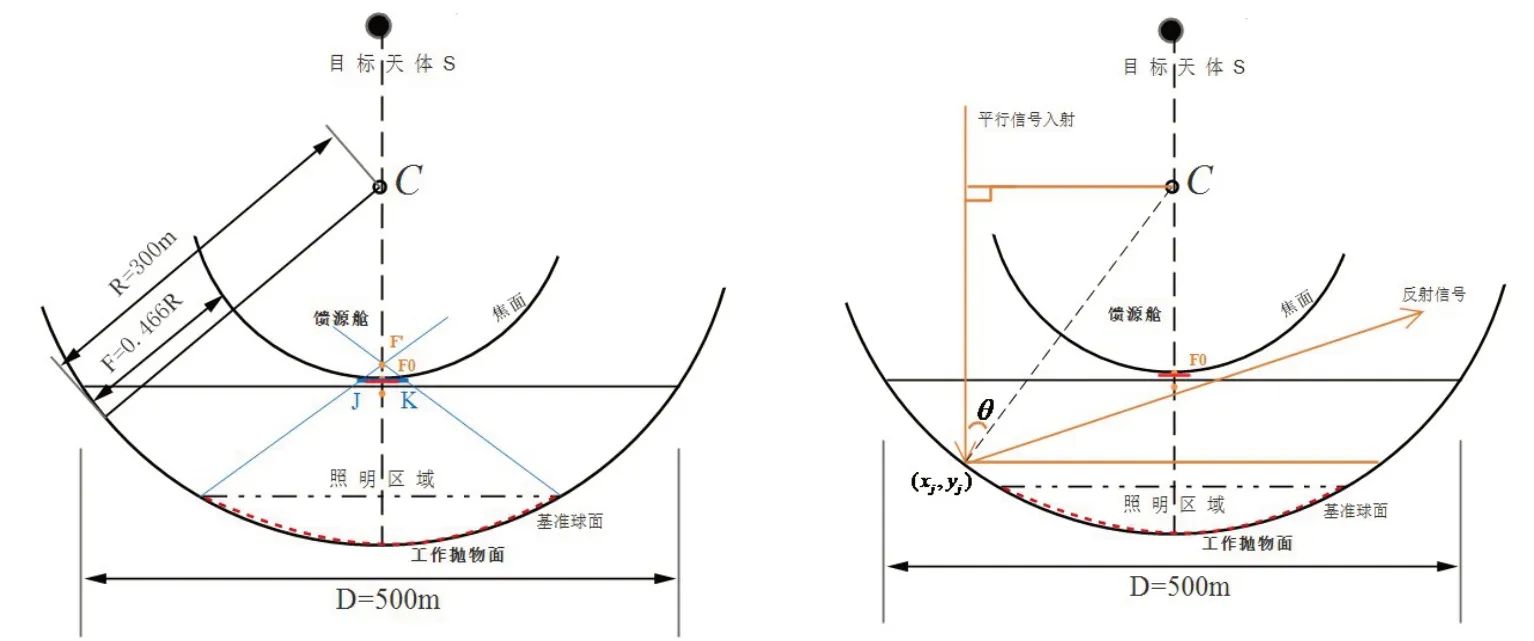
图2 馈源舱及基准反射球面接收比计算方法示意图
3 灵敏度分析
本模型可视为由2个变量f、h决定的优化模型,优化指标为3个:促动器的伸缩量之和、主索节点到理想抛物面距离与所对应圆弧长之差的和、抛物线与基准圆交点口径[15].
在此把主索节点促动器伸缩量之和作为主要优化指标,由方案二的遗传算法可以得出f2=0.469 0,h2=0.455 2为最优方案.取f0=0.466 0,h0=0.60为起始点,向最优点移动Δ,变化后的坐标为:把变化后的变量代入3个指标的函数计算得,通过建立相关模型,求出伸缩量变化率为-2.56%,口径变化率为9.68%,弧长差变化率为-9.11%.表明3种评价指标对(f,h)的变化不敏感,模型较为稳定.
4 总结
文章结合FAST相关节点数据,基于截痕法、遗传算法和旋转矩阵法等建立FAST主动反射面调节模型.通过比较工作态馈源舱与基准态反射球面的接收比P1=0.749 8,P2=0.071 8的结果,可以发现馈源舱的接收比明显要比基准反射球面的接收比大得多,说明求出的工作抛物面可以使得馈源舱接收更多的反射信号,文章提出的主动反射面的变形方案较为理想.另外,文章对FAST主动反射面的形状调节策略做较为完整的分析,综合考虑包括下拉索对主索节点经纬向位移偏移误差的影响、工作抛物面与基准球面过渡是否平滑等多种因素,对于实际的射电望远镜、主动反射面等相关内容有一定的借鉴意义.

