宁波地区典型地层HSS 模型参数试验研究

叶俊能 ,刘干斌 ,骆睿栋 ,高 游 ,陆 幸

（1.宁波市轨道交通集团有限公司,浙江 宁波 315010;2.宁波大学 岩土工程研究所,浙江 宁波 315211）

地下空间的开发已然成为城市建设的重点方向,一方面基坑工程的规模越来越大,另一方面基坑工程向超深方向发展[1].宁波市位于长江三角洲南翼,濒临东海,土质属于典型的海相沉积软土.宁波市区建筑物密集,地下管线错综复杂,在这种条件下进行基坑的开挖工作,除了需要关注基坑开挖本身的安全性外,开挖过程中对周围环境和建筑物的影响也需引起重视.随着基坑工程规模和难度的不断增加,数值方法逐渐成为基坑变形分析最为有效的方法之一[2].

在数值方法计算过程中,选择合适的本构模型和准确的模型参数至关重要.其中,HS 模型[3-4]适用于敏感环境下的基坑开挖数值分析,且近年来使用率不断提高.在此基础上,Benz[5]对HS模型进行了修正,得到了HS-Small 模型(简称HSS 模型).修正后的模型考虑了土体剪硬性和压硬性在土体开挖过程中产生的影响;同时,在小应变范围内还考虑了剪切模量随应变的减小而衰减的行为.而HSS 模型参数的选取在很大程度上影响着模拟结果的准确性,因此,王卫东等[2]进行了一系列室内土工试验,较为完整地获得了上海浅层土层的HSS 模型参数,并结合相关工程实例对参数的准确性进行了验证.梁发云等[6]通过对工程实例进行数值分析,验证了HSS 模型参数的确定方法及其适用性.司马军等[7]通过室内试验,较完整地获得了武汉地区老黏土HSS 模型参数,指出HSS 模型可以模拟超固结土的峰前力学行为.林乔宇[8]通过对厦门花岗岩残积土进行一系列试验研究,较为完整地获得了该类型土的HSS 模型参数,并对相关参数进行了敏感性分析.张骁等[9]根据土工试验初步拟定了苏南地区各典型土层的HSS 模型参数,对参数作了进一步优化,并结合数值模拟的结果提出了相应工程防护措施.张卫兵等[10]通过反演的方法获得了银川地区典型土层的HSS 模型参数,并基于该参数进行了数值模拟.

目前,关于宁波地区软土HSS 模型参数的研究较为欠缺,现有工程应用中的HSS 模型参数多采用经验取值,但经验取值存在参数范围较大、不够精确的缺点.本文通过一系列室内土工试验,对宁波地区HSS 模型参数进行较为系统的研究,获得了宁波地区典型土层的HSS 模型主要参数,即淤泥质粉质黏土层②、③,粉质黏土层④、⑥、⑦,和含粉砂粉质黏土层⑤的HSS 模型关键参数,最后详细分析了各土层HSS 模型关键参数间的关系,可为后续宁波地区基坑开挖等数值模拟中的参数选择提供基础性的参考数据.

1 HSS 模型简介

HSS 模型即硬化土小应变模型,是Benz[5]在HS 模型的基础上,结合修正的Hardin-Drnevich 剪切模量关系[11]改进得到的.相较HS 模型,它考虑了小应变范围内刚度和应变的非线性变化关系.HSS 模型共包含13 个参数,其中11 个为HS 模型参数,另外2 个为小应变相关参数.其中:K0为正常固结条件下静止侧压力系数;ψ为土的剪胀角;m为刚度应力水平相关幂指数;pref为参考应力;νur为加卸载泊松比.上述5 个参数可根据经验或者公式取值[6],见表1.

表1 HSS 模型部分参数的取值

此外,还有8 个参数可以根据室内试验进行量测:为参考切线模量;为参考割线模量;Rf为破坏比;为参考加卸载模量;c′为土的有效黏聚力;φ′为土的有效内摩擦角;为参考初始模量;γ0.7为割线剪切模量衰减到初始剪切模量70%时所对应的剪应变.

2 试验材料及仪器

试验土样取自宁波海曙区,取土土层分别为②、③、④、⑤、⑥、⑦层,取土深度分别为6～7、19～22、25～30、46～51、57～62 和68～72 m.三轴试验和弯曲元试验试样为直径50 mm、高度100 mm的三轴样,固结试验试样为直径61.8 mm、高度20 mm的环刀样.各层土样的基本物理力学参数见表2.

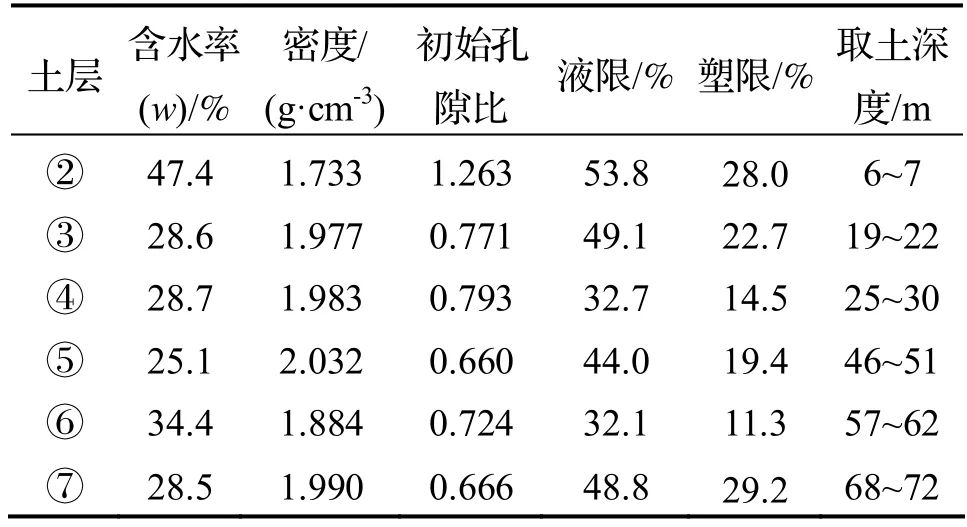
表2 土层基本物理力学参数

HSS 模型参数中K0、ψ、pref、νur和m可参照已有经验进行取值,具体取值方法见表1,本文重点是确定其他8 个参数.针对宁波软土,通过以下4 部分试验来确定这些参数: (1)标准固结试验获得参数;(2)常规三轴不排水剪切试验获得参数c′和φ′;常规三轴排水剪切试验获得Rf和;(3)三轴固结排水加卸载剪切试验获得参数;(4)弯曲元试验获得参数和γ0.7.

标准固结试验采用常规固结仪,8 级荷载逐级加载: 12.5、25、50、100、200、400、800、1 600 kPa,每级加荷时间为24 h.常规三轴排水/不排水剪切试验采用全自动三轴仪,三轴固结排水加卸载剪切试验和弯曲元试验采用动三轴仪器和弯曲元设备,试验步骤依据土工试验方法标准[12].

3 试验结果分析

3.1 参数 的确定与分析

图1 表示各土层轴向荷载与轴向应变的实测点与拟合曲线.实测点数据由标准固结试验测得,线条为拟合曲线(R2均为0.99).图中1、2 和3 表示3 组平行试验,要获取参考切线模量需对实测点进行拟合.拟合曲线采用一元三次方程[8]:

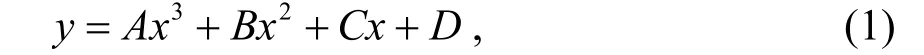
式中,A、B、C和D为拟合参数.根据每层确定参数的试验曲线拟合函数,求得轴向荷载为100 kPa时曲线的斜率,该斜率即为参考切线模量.根据图1 即可求得各土层参考切线模量.其中,⑤层土3 号拟合曲线的离散性较大,这是因为⑤层土土质不均匀,土中存在较多砂粒和碎石,故3 号取土孔所取的土与1、2 号取土孔所取的土存在较大差异,故导致数据产生了较大离散性.表3 汇总了各土层参考切线模量与压缩模量Es1-2.

表3 各土层的 和Es1-2值 MPa

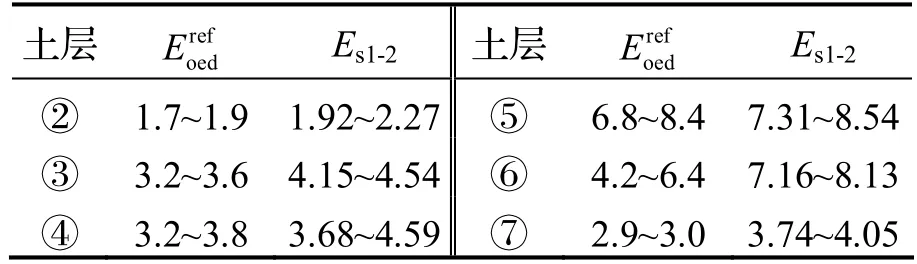
表3 各土层的 和Es1-2值 MPa

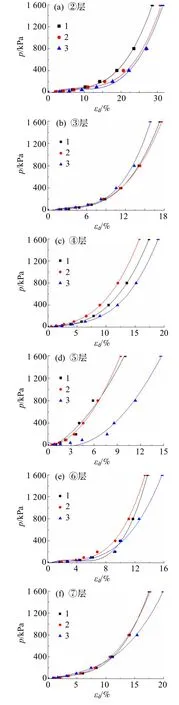
图1 轴向荷载与轴向应变关系曲线

图2所示为宁波地区及其他地区土体的和Es1-2关系曲线.由图可知,宁波地区土体的为Es1-2的0.83 倍,厦门含砂黏土为0.7 倍[8],上海淤泥质黏土为0.9 倍[13],北京粉质黏土为1.1 倍[14].各土层和Es1-2的比例关系较为接近,没有表现出很大的离散性.目前在实际应用中,对于参数,一般与Es1-2取值相同.对于包括宁波在内等多地的参数间比例关系进行分析后可知,该方法是可行的.

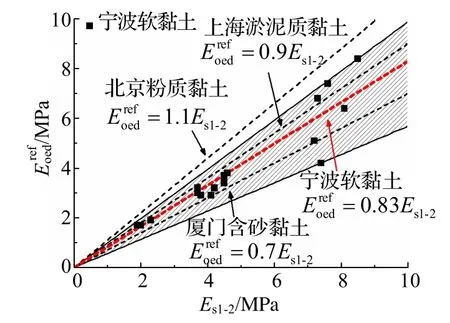
图2 和Es1-2关系曲线

3.2 参数 和Rf的确定与分析

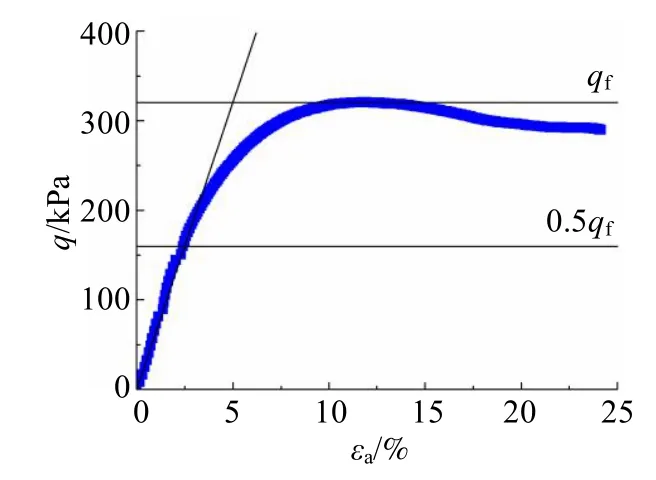
图3 应力—应变曲线

破坏比Rf的确定: 将HS 模型中偏应力和轴向应变的双曲线关系[11]转换成εa/q—εa直线关系:

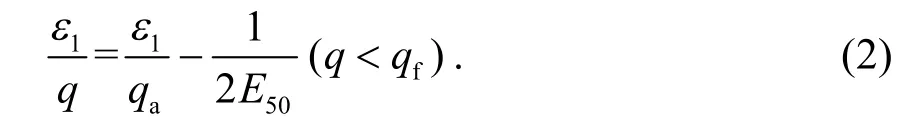
在转换过程中,为了提高准确性,使直线通过q/qf=70%和95%的点,绘制出εa/q—εa关系曲线,直线斜率的倒数即为qa,故破坏应力比Rf=q/qf,图4 给出了宁波各土层的εa/q—εa关系曲线.由图可以看出,各土层的εa/q—εa关系几乎为线性关系,第⑤层斜率最大,即qa最小.

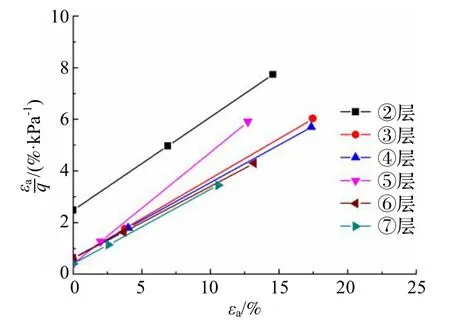
图4 εa/q—εa 关系曲线

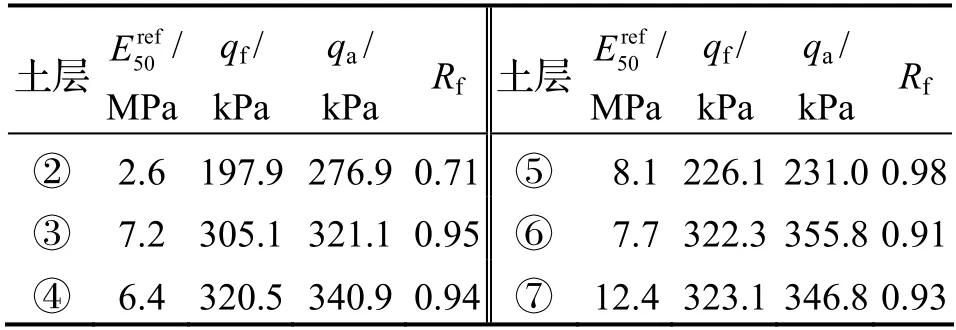
表4 各土层的qa 和Rf值

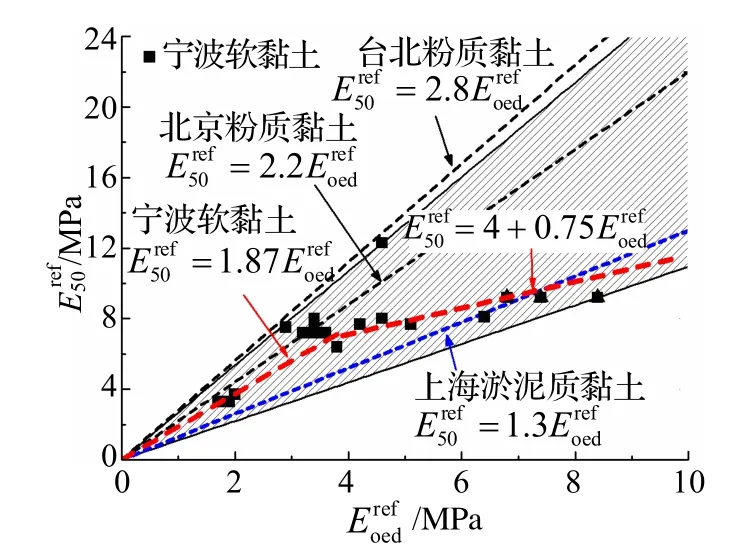
图5 和 关系曲线

3.3 参数 的确定与分析

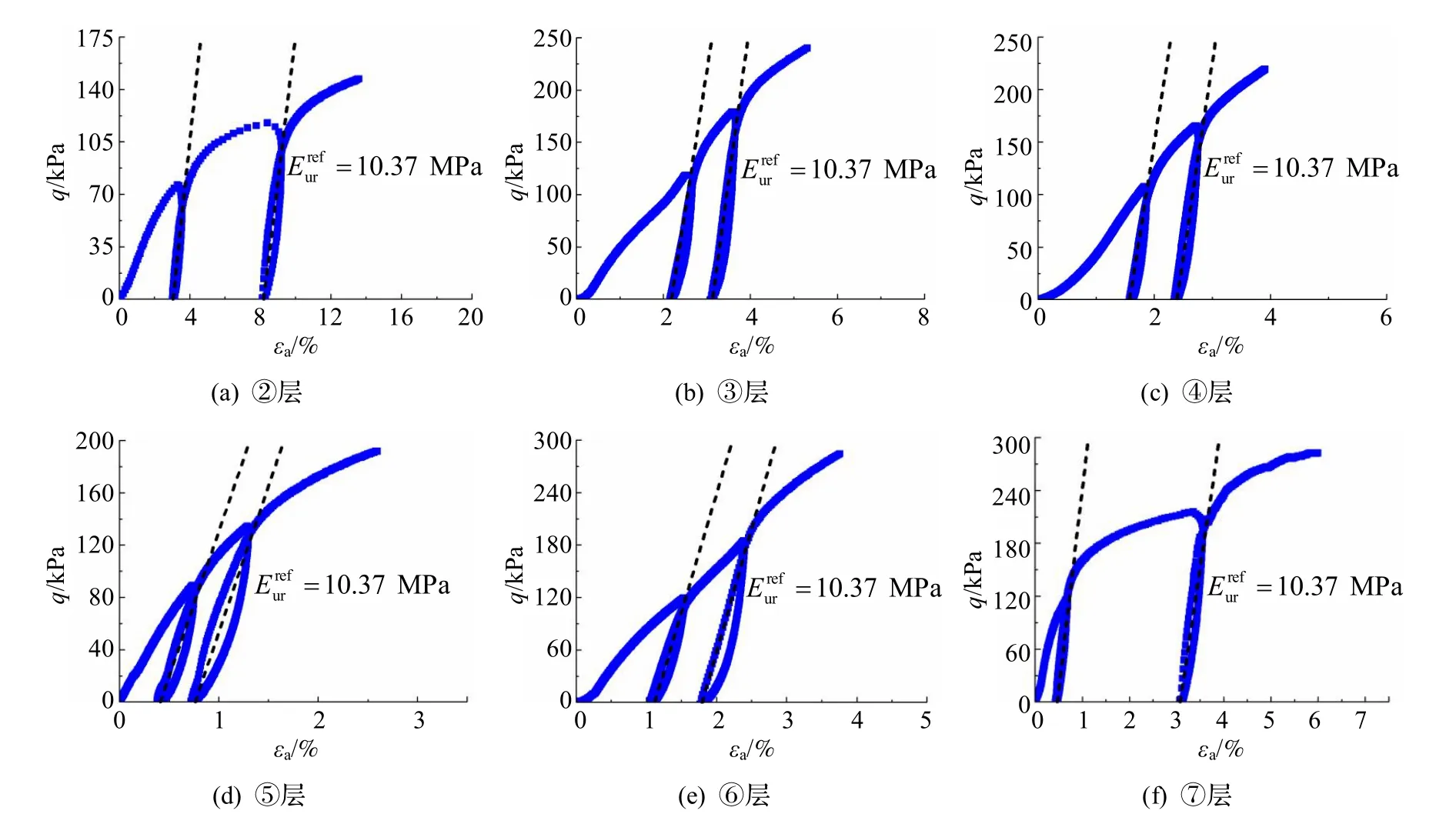
图6 各土层应力—应变曲线

3.4 参数c′和φ′值的确定

通过常规三轴固结排水剪切试验获得土体的值,试样的围压根据不同埋深来确定,若原状土试样的原位有效竖向应力为,则有效等向压力值的计算公式为:

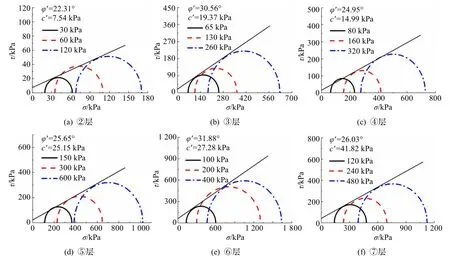
图7 各土层莫尔应力圆

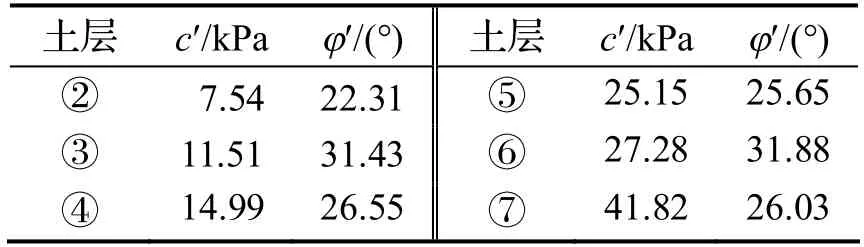
表5 各土层的c′和φ′值

3.5 参数 和γ0.7的确定与分析

图8 为参考围压在100 kPa 下,各土层的弯曲元试验波形.本次试验中,剪切波的传播时间通过峰值法(P-P 法)来确定,即发射波和接收波第一个波峰间的时间间隔t,实际计算中的时间间隔还应扣除仪器空接时产生的误差.完成固结后,在计算机中打开GDS BES 软件,输入试样的高度、采样频率及采样时间,选择正弦波作为激发信号,并输入发射波的频率,本次试验发射波频率选为2 kHz,剪切波速可根据下式求得:

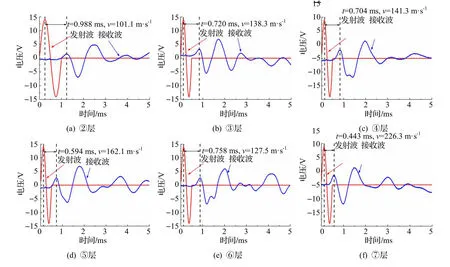
图8 各土层弯曲元波形图

式中,L为试样的高度.小应变剪切模量可根据土体密度ρ和Vs由下式求得:

根据Brinkgreve 等[19]的介绍,参考应变γ0.7可由下式表达:

表6 各土层的 和γ0.7值

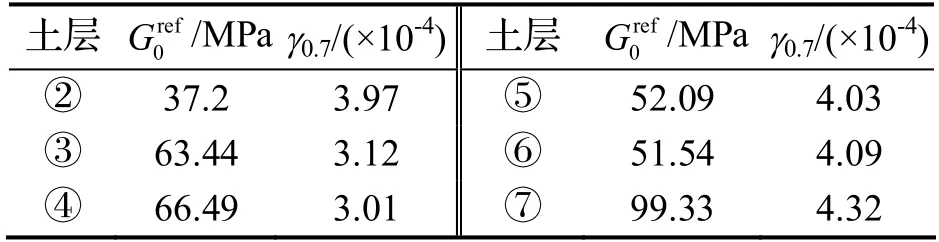
表6 各土层的 和γ0.7值

4 结论

本文通过一系列室内土工试验,获得了宁波地区典型地层的HSS 模型参数及主要模型参数之间的比例关系,主要结论如下: