基于模糊PID控制的差动AGV稳定性控制研究

吴瑞明,冯浩然,傅阳，陈凯旋，李阳，程强

(浙江科技学院机械与能源工程学院，浙江杭州 310023)

0 前言

随着物流与仓储行业的快速发展，企业与工厂运输货物效率亟待提高，传统生产运输方式逐步被淘汰，自动引导车(Automated Guided Vehicle，AGV)的应用与开发得到了越来越多的关注，并应用于各个领域。

AGV在智能制造业中占有极其重要的地位，是现代智能仓储和物流系统的关键组成部分。AGV作为一种物流运输的移动机器人，正广泛应用于物流仓储、烟草行业等领域中，它能够根据规定路线自动行驶，将货物搬运到指定位置。AGV小车具有自动化程度高、柔性化程度高以及可靠性强等优点，能够提高工厂的自动化水平，提高生产效率，降低生产成本，已经成为现代物流仓储、自动化生产线不可缺少的重要设备。依据机器人获取环境信息的方式又可以将导航方式分为：GPS导航、激光导航、惯性导航、视觉导航等。AGV运动控制算法主要可划分为：适用于线性或简单非线性系统的模糊PID控制,适用于精确系统模型的线性系统的LQR控制和适用于线性或简单非线性系统及最优解滚动优化的MPC控制。

面向实际仓储和物流复杂环境下的行驶应用需求，设计了一辆AGV小车，用西门子PLC控制机械手实现搬运功能，小车能够实现跟随、避障，满足多种不同型号产品配送需求。设计采用视觉导航方式，将CCD摄像机安装在车身前部以实时获取环境信息，并通过地标(黑色胶带和二维码)发送到工控机，工控机处理信息并控制PLC操作。

所研发的AGV可以实现车间物流作业，但由于实际运行转向时会出现转向不稳定的问题，因此对该AGV定点自转进行研究，确定影响参数并进行优化，选择模糊PID控制，实现AGV稳定转向控制。

1 AGV底盘运动学

所研究的两驱动轮差动传动AGV的前侧为机械手装置，机身内存放电池组、工控机、西门子S7-1200PLC和中大24 V直流无刷电机驱动器BD15L等模块，底盘模型如图1所示，底盘运动学模型如图2所示，由于六轮结构比三轮或四轮结构具有更大的承载能力和更好的稳定性，因此采用双轮的六轮机构。后轮和前轮是两个万向轮，中间是两个驱动车轮，驱动轮由直流无刷电机驱动，转向由两电机的差动控制。

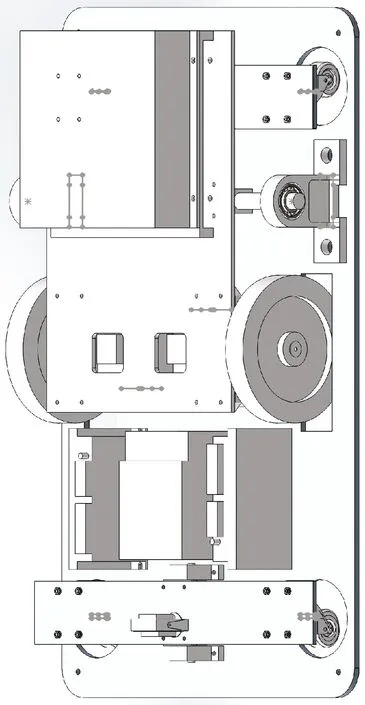
图1 AGV底盘模型

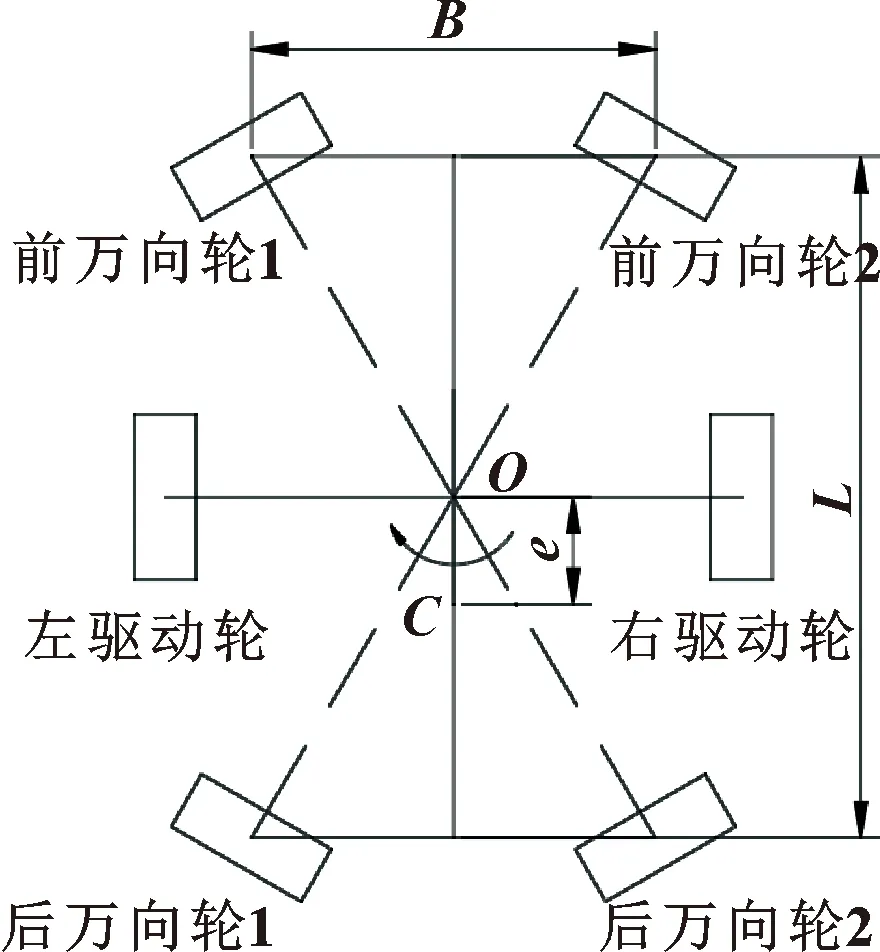
图2 底盘运动学模型

在图2中，AGV前后两侧有4个万向轮，车体的质量中心在点处，设AGV总质量为,前后轮距离为，左右轮距为,偏心距为，质心高度为，静摩擦因数为，滚动摩擦因数为，左右驱动轮水平距离为。对AGV的定点加速度转向过程进行受力分析，如图3所示。

图3 AGV受力分析简图

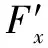
R4=0

(1)

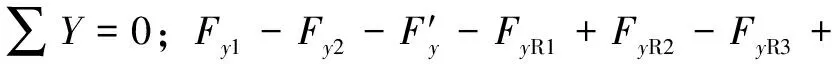
R4=0

(2)

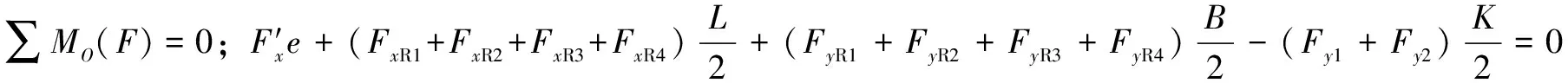
(3)

由于在相同的路面环境下，AGV两侧的垂直载荷是相同的，所以驱动轮1和2在方向上的静摩擦力是相等的，则由方程(1)可得：

(4)

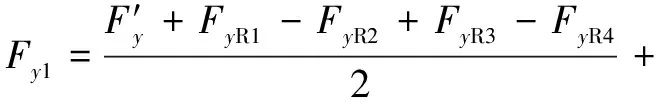
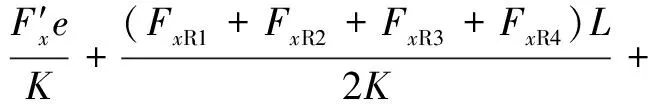
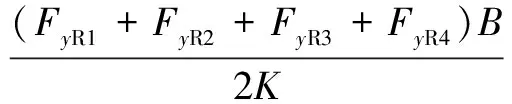
(5)

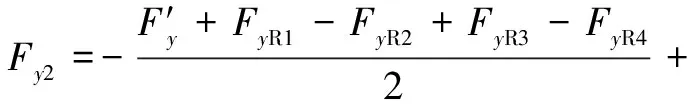
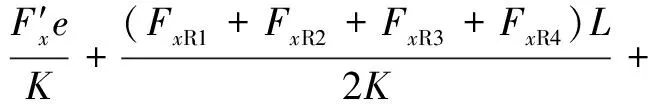
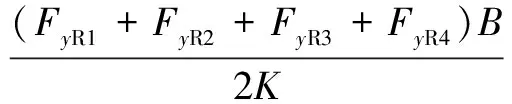
(6)

2 AGV转向稳定性分析

2.1 侧滑

对于AGV侧滑的情况，由方程(1)和(2)可以看出，当AGV在转向过程中加速时，在方向上，左右驱动轮的最大静摩擦力小于AGV受到其他力的总力，则会导致AGV存在侧滑的情况。为了确保AGV运行稳定，应避免这种情况，因此：

(7)

将AGV相关参数代入式(7)，化简后：

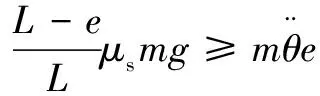
(8)

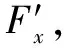
2.2 驱动轮滑动

当驱动轮减速或转动时受到路面的扭矩不足时，驱动轮会发生滑移情况。因此，为避免滑动的发生：

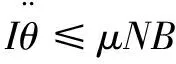
(9)

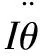
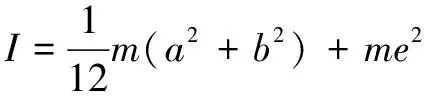
(10)

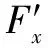
(11)

从式(11)可得:AGV总质量、前后轮距离、左右轮距、偏心距、质心高度、静摩擦因数及角加速度都会影响AGV的定点自转。

2.3 驱动轮间的加速度差异

左驱动轮转动受力分析如图4所示。

图4 左驱动轮受力分析

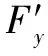
(12)

∑=0;--=0

(13)

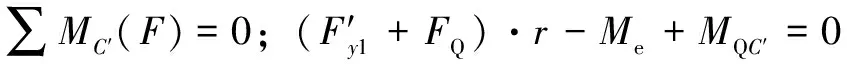
(14)

根据上述方程，可得：

(15)

同理，右驱动轮的角加速度为

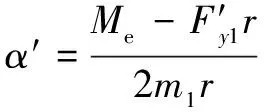
(16)

分析可得两个驱动轮的角加速度都会影响AGV的定点自转。

3 AGV仿真分析与优化

3.1 AGV运动仿真

为分析所研究的AGV动态特性影响因素，在SolidWorks中建模，然后导入ADAMS进行运动学仿真，简化不影响AGV稳定性的圆角和倒角以及不影响AGV强度和刚度的元件；减少模型中零件的数量，通过设置一些连接部件加快计算速度；仿真模型包括AGV模型及其相应的运行环境，AGV车轮与其运行道路接触处建立矩形模块。AGV车体框架采用6061钢材制作；车轮采用聚氨酯制作；路面采用混凝土制作，其他材料的质量根据实际质量直接在软件中设置。所研究的AGV实体如图5所示，SolidWorks模型和ADAMS模型分别如图6和图7所示。

图5 AGV实体

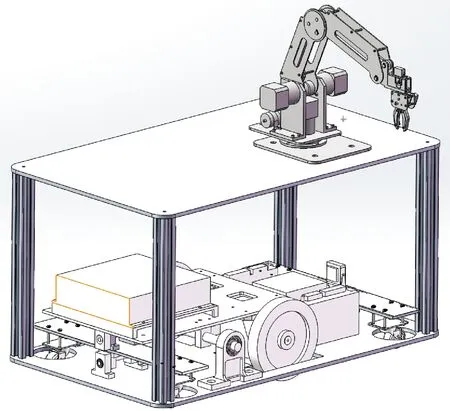
图6 SolidWorks模型

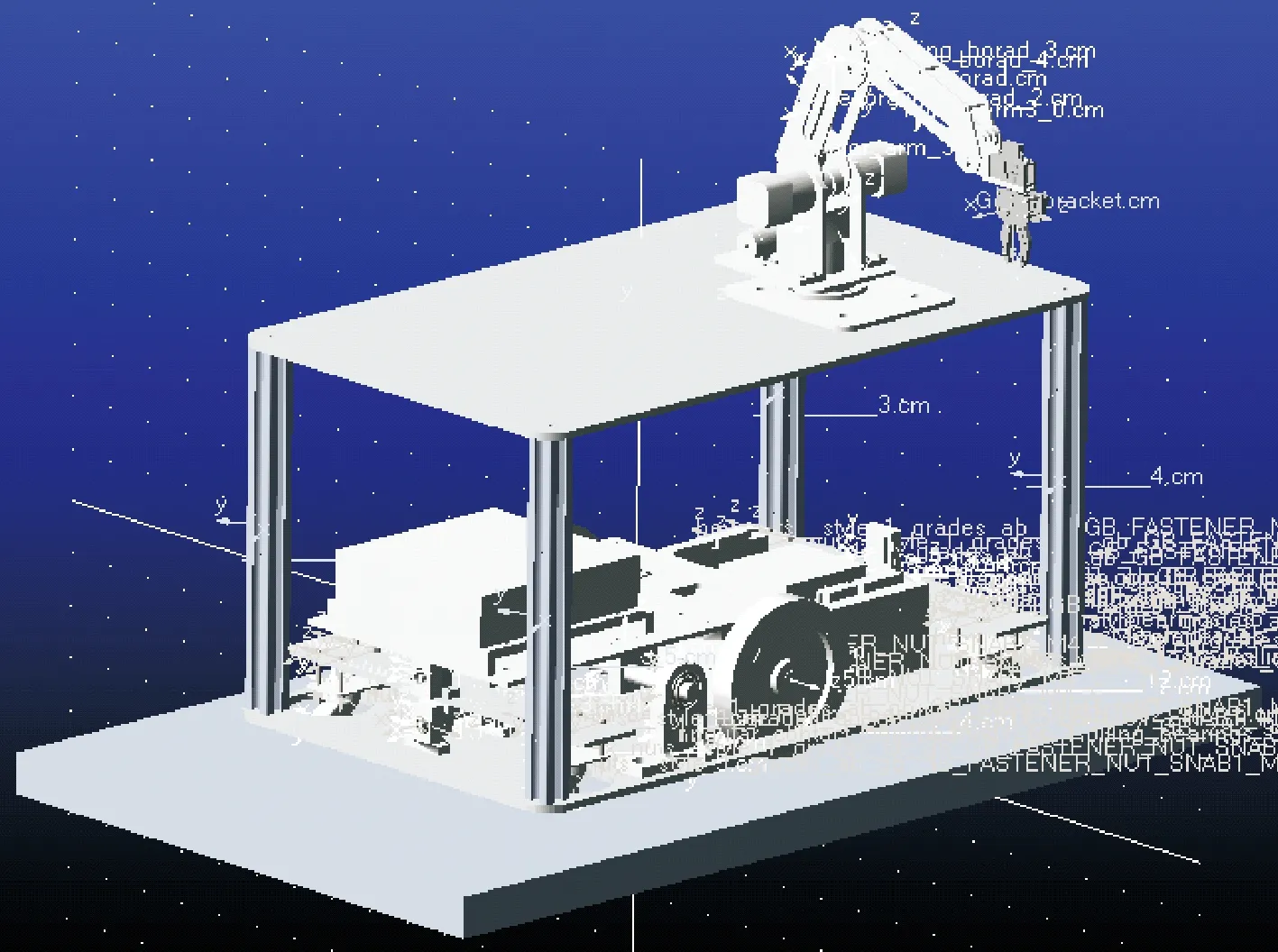
图7 ADAMS模型

3.2 转向影响因素的优化

根据所得的AGV运动影响因素，为了分析AGV定点自转稳定性，通过仿真，输出驱动轮不同角速度和角加速度下与自转中心点的最大偏差，分别如图8和图9所示。

图8 不同角速度的定点中心偏差 图9 不同加速时间的定点中心偏差

从图8可以看出:当AGV在转向时处于低速时，旋转中心的最大偏差极小;而随着速度增加，偏差随之变大。因此，为了保证稳定转向，同时提高AGV的工作效率，驱动轮的角速度可选择28～32 rad/s之间。进一步分析驱动轮角加速度对AGV的运动影响，对AGV从0到30 rad/s不同加速时间下的偏移量进行分析，仿真结果如图9所示。可看出：当加速时间小于0.4 s时，AGV旋转中心最大偏差很大；在0.4 s之后，偏差较小且处于相对稳定状态。综上，与上述理论分析一致。

再通过控制其他条件不变，对不同静摩擦因数下的离中心点最大偏差量进行仿真实验，如图10所示。可以看出：静摩擦因数对AGV定点转向影响较大，当静摩擦因数为0.1时，AGV转向极其不稳定，旋转中心的最大偏差接近36 mm；静摩擦因数为0.6左右时，AGV转向相对稳定。在仿真中，驱动轮与地面的静摩擦因数对AGV定点转向的影响符合理论推导。在实际应用中，不改变车轮材料情况下，AGV与地面的静摩擦因数与0.6接近，因此，不需要改动车轮和地面的情况下，静摩擦因数满足AGV运行作业的稳定性要求。

图10 不同静摩擦因数的定点中心偏差

因此，为了保证稳定转向，同时提高AGV的工作效率，驱动轮的角速度选择30 rad/s，在此加速度下的减速时间设定为0.4 s。

3.3 AGV转向控制设计优化

AGV控制系统组成如图11所示。控制单元选择西门子S7-1200 PLC，跟踪单元选择CCD视觉传感器进行视觉导航，通信单元采用RS485通信，驱动单元采用两个中间驱动轮差动驱动。驱动电机是AGV驱动力的主要来源，驱动电机决定AGV的功率性能和负载能力，从性能方面选择直流无刷电机作为AGV驱动电机。

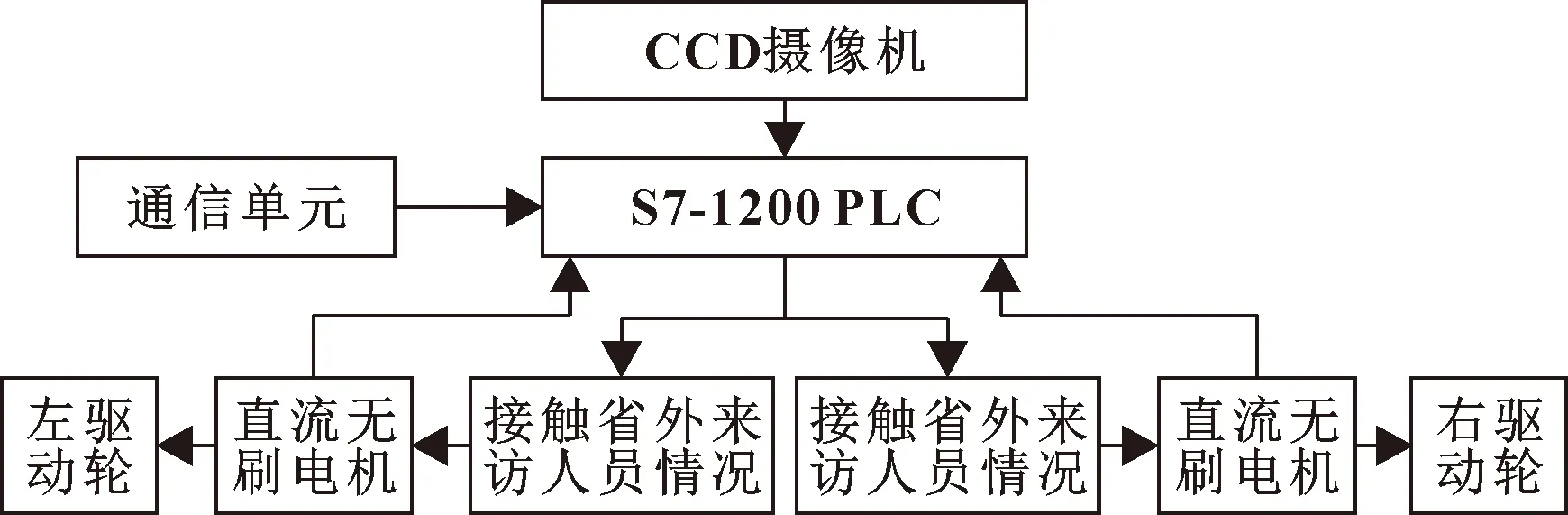
图11 AGV控制系统组成

所研究AGV的总质量约50 kg，机械手搬运质量为5 kg。因此，满载AGV对地面的压力为550 N, 由于AGV的运行环境是水平地面，因此不需要考虑斜坡阻力，且由于AGV的运行速度很低，空气阻力可以忽略不计。因此，在运行过程中，AGV只需要克服加速过程中的滚动摩擦和加速阻力：

∑=+

(17)

式中:是AGV的滚动阻力;是加速阻力。因远小于，因此将它忽略。AGV的设计最大加速度为2 m/s，则加速阻力==55×2 N=110 N。

AGV驱动轮的半径为0.075 m，可得总阻力矩∑=×=110×0.075=8.25 N·m。经过参数优化后的AGV仍存在结构偏心问题，为进一步提高AGV的转向稳定性，研究AGV定点转向的控制策略。

通过CCD视觉传感器检测AGV旋转时离定点的偏差，计算当前偏差与上一次偏差的偏差值。通过实验得到转向过程中最大偏差值为15 mm；其基本论域为[-80,80]。然后将其模糊化，转化为模糊集论域[-3，-2，-1，0，1，2，3]，用模糊语言表示为{NB，NM，NS，ZO，PS，PM，PB}。同样，对于模糊输出Δ、Δ和Δ，首先通过调试确定其基本论域，然后同样进行模糊化，采用相同模糊语言表示。

而对于去模糊，选择采用重心法，将得到的隶属度A()、B()和对应的横坐标代入下面的方程，求出模糊推理的最终输出值。

(18)

经调试，AGV转向稳定性有所提高，能满足实际工作要求。图12为AGV实际运动的轨迹偏差。AGV在=5～8 s内转弯，最大偏离起始距离为4 mm，经调整后，偏差减小到小于2 mm。初始AGV的最大偏差以及运行过程中的调整效果均达到了预期。

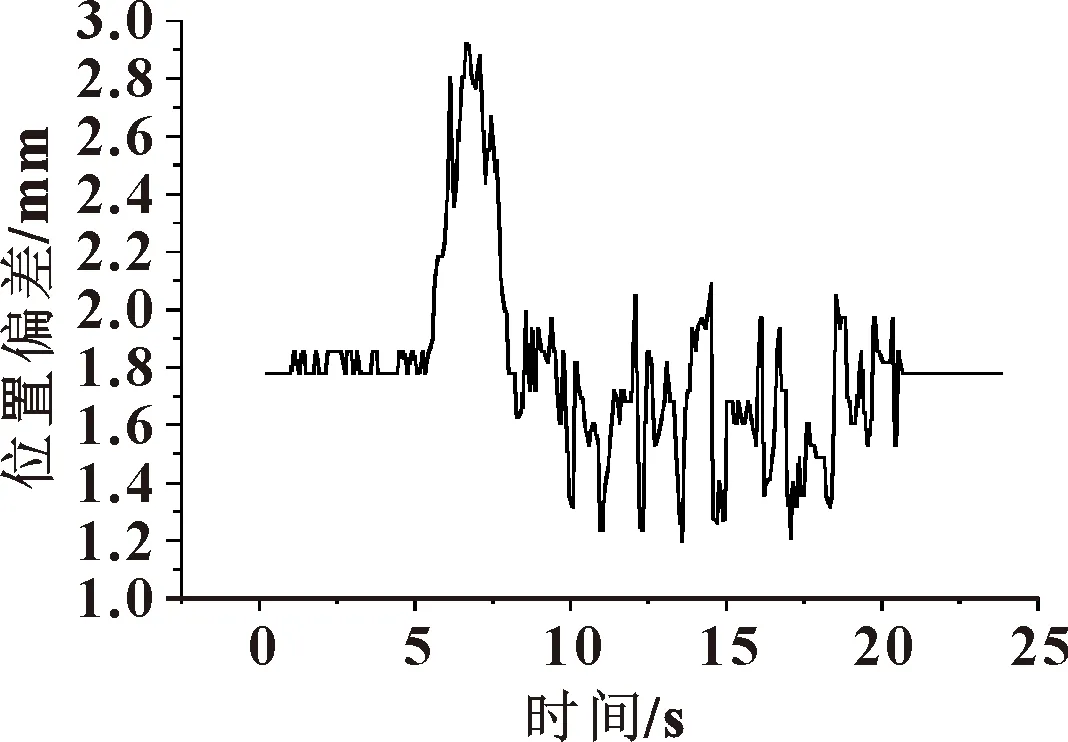
图12 AGV轨迹偏差

4 结语

针对AGV定点自转不稳定问题，从理论上分析了AGV定点转向的3种不稳定情况：AGV定点转向过程时的滑移问题，驱动轮的滑移问题以及两驱动轮间加速度的差异。建立了对应的物理模型和数学模型，确定影响AGV定点转向稳定性的结构和运动参数：转向角速度、加速度、偏心率、地面与驱动轮之间的静摩擦因数以及AGV转弯时的转动惯量与AGV的大小和质量有关；然后建立AGV模型，分析了速度、加速度和静摩擦因数对AGV定点转向稳定性的影响。研究发现，驱动轮的角速度选择30 rad/s时，既可以保证稳定转向，也同时提高AGV的工作效率；当将AGV驱动轮角速度从0提升到30 rad/s的加速时间小于0.4 s时，AGV旋转中心的最大偏差显著增加，AGV滑动；当AGV驱动轮与地面的静摩擦因数从0.1增加到0.3时，AGV的转向稳定性显著提高。这与理论推导的结果一致，验证了理论推导的合理性。再选择模糊PID控制算法设计相应的转向控制策略，经调试，优化后的AGV转向工作稳定，满足实际工作要求，为提高AGV的稳定性和安全性提供理论依据和设计思路。