基于约束扰动观测器的感应电机鲁棒模型预测控制方法

姚阳，杨朝翔

(国网冀北综合能源服务有限公司，北京 100045)

0 前言

随着现代工业对电气传动系统性能要求的不断提高，国内外对高性能电机驱动的研究也日益深入。串级控制结构是一种广泛应用的高性能电机驱动方式，主要包括内环转矩控制和外环转速控制。其中，转矩控制广泛采用基于模型预测控制(MPC)的各类算法，如通过将MPC与直接转矩控制(DTC)相结合，有效替代了传统的线性电流控制策略。文献[5]提出了一种有限控制集MPC(FCS-MPC)方法，利用一组有限电压矢量进行优化，每次采样过程中选择最佳的电压矢量，由于直接考虑了逆变器的开关状态，FCS-MPC的控制性能与经典DTC方法相近。文献[6]通过引入空间矢量脉宽调制技术，采用连续控制集MPC(CCS-MPC)实现了感应电机的高性能转矩控制，相较于FCS-MPC方法，CCS-MPC具有转矩脉动小、谐波失真小等优势。

除转矩控制器外，优良的速度控制技术也是高性能电机驱动的关键。其中，基于各类观测器的速度控制方法以其结构简单、易于实施且性能优良，得到了广泛应用。文献[8]基于扩展状态观测器(ESO)，提出一种反演滑模控制策略，实现了扰动环境下永磁同步电机的鲁棒速度控制。文献[9-10]基于小增益定理和频域分析，提出结构简单、抗干扰性能优良的扰动观测器(DOB)，实现了感应电机的转速控制。文献[11-12]基于奇异摄动理论，在离散时域内设计了相应的DOB，但未对观测器的鲁棒性进行分析。文献[13]采用Luenberger观测器，有效减小了MPC方法的稳态误差，但未考虑参数不确定性的影响。文献[14]将FCS-MPC与连续时间DOB相结合，提高了FCS-MPC的性能，但未进行离散时域分析。

本文作者针对感应电机(IM)高性能驱动控制方法的需求，基于串级控制结构，提出一种由内环转矩控制和外环速度控制组成的感应电机鲁棒速度控制器。对于内环转矩控制，在已有CCS-MPC方法的基础上，通过考虑系统参数随转速的变化，基于线性矩阵不等式提出改进的CCS-MPC方法，在保证控制性能相同的前提下降低计算成本。对于外环速度控制，在考虑转矩限制、力学模型参数不确定性和负载转矩扰动的情况下，将稳定化MPC与DOB相结合，在离散时域内设计约束DOB，并给出相应的定理和推论，证明所提出的速度控制器的稳定性及其条件。通过物理实验对所提控制方法进行验证。

1 IM模型及其运行方式概述

1.1 IM数学模型

静止坐标系中的IM模型可由公式(1)进行描述：

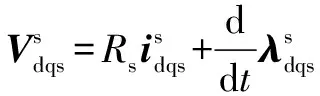
(1a)

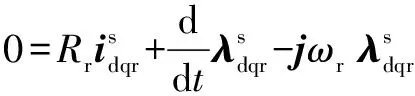
(1b)

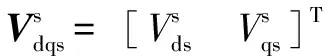
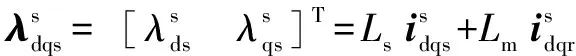
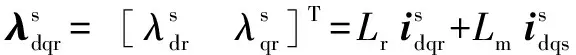
其中：、及分别为定、转子绕组自感及定、转子绕组互感系数。IM转矩可表示为公式(2)：

(2)

式中：为极对数；=/。

经典的磁场定向控制通常在同步坐标系中设计控制器。当采用转子磁链定向控制(RFOC)时，公式(1)中的各矢量需转换至同步坐标系中，例如：

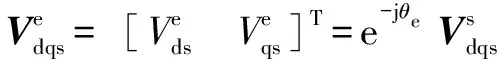
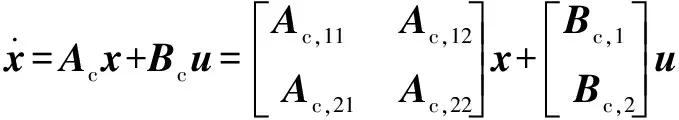
(3)

其中：

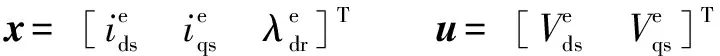
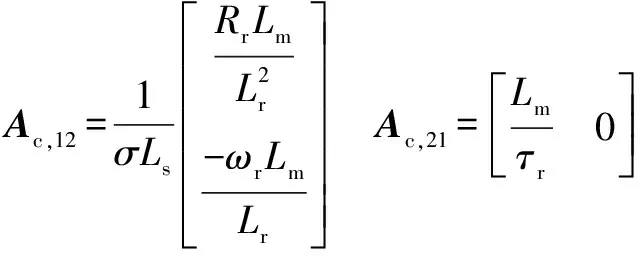
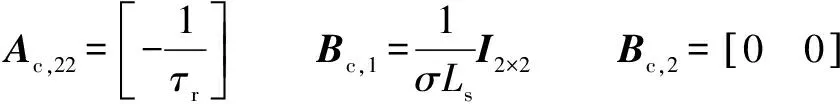
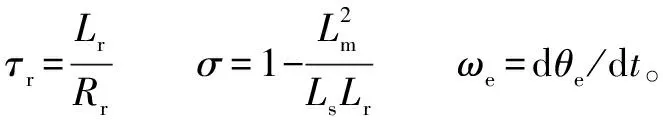
进一步，IM转子转速由下述不确定模型给出：

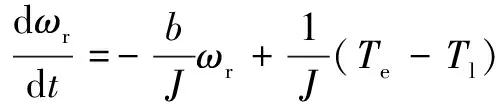
(4)

其中：和分别表示转动惯量和黏滞摩擦系数；表示负载转矩。负载转矩和模型参数在实际中通常是不确定的，为便于后续讨论，对不确定参数和引入如下假设：

假设1：不确定参数>0和>0属于如下已知有界集：

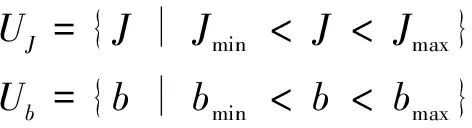
1.2 IM运行模式

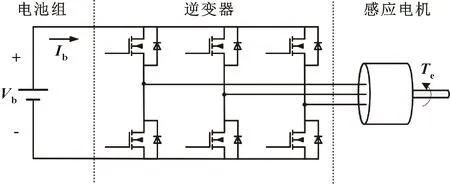
图1 采用电池组及逆变器的IM供电模式

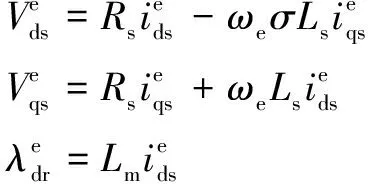
(5)

进一步，可得出IM稳态转矩为

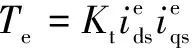
(6)

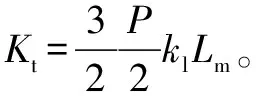
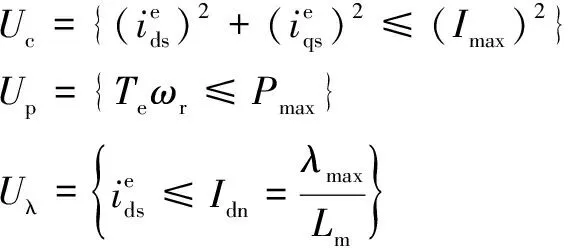
(7)

其中：表示逆变器的电流极限；表示IM磁通极限；表示IM在安全运行区域内的输出功率极限，此时逆变器应在极限范围内工作，=，其中是直流链路中电池馈送至逆变器的最大输出电流。

基于公式(7)，IM的工作区域可分为恒转矩(CT)区域和恒功率(CP)区域。对于每个区域，最大可用扭矩为()由公式(8)计算：

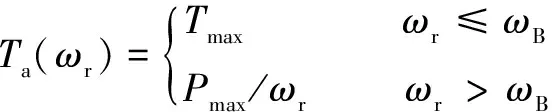
(8)

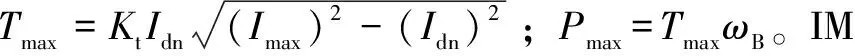
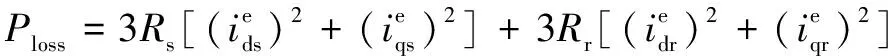
(9a)

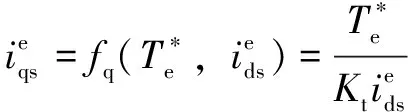
(9b)

2 转矩控制器设计

利用公式(3)，应用Euler近似方法获得IM的离散时间模型：

(+1)=()()+()

(10)

其中：()=()+；=；为采样间隔；∈，为自然数集。此外，()应属于如下集合：

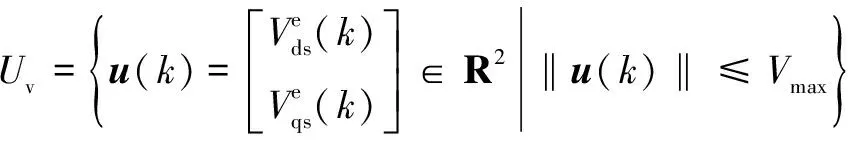
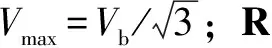
2.1 CCS-MPC方法设计

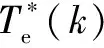
其中：

(11)

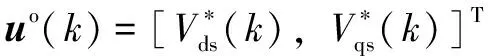
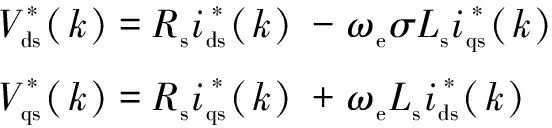
(12)

且有：

()=()()+()

(13)

由公式(11)—(13)，给出单步损失函数：

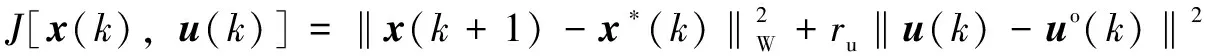
(14)

基于上述公式，可将CCS-MPC的设计归结为求解如下约束优化问题：

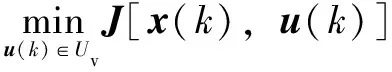
(15)

上述优化问题的解可表示为

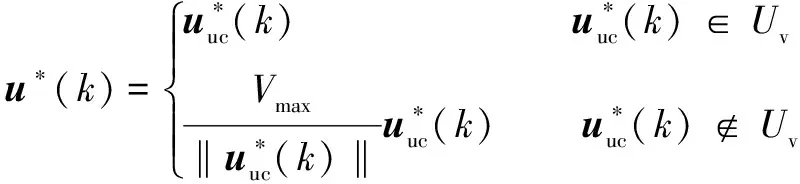
(16)

其中：

{-[()()-()]+()}

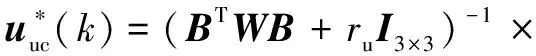
(17)

为优化问题(15)的无约束解，可通过求解∂[(),()]/∂()=0得出。

公式(14)中权重矩阵的确定应遵循如下规则：在和转矩参考值不变的情况下，当稳态控制输入施加至被控对象时，应使代价函数[(),()]单调减小；然后，通过求解优化问题(15)确保代价函数进一步减小。设()=()-表示状态跟踪误差，将公式(10)与公式(13)相减可得出：

(+1)=()()+[()-]

(18)

令()=，有：

[(),]=(+1)(+1)=

()()()()

(19)

且：

()[()()-]()

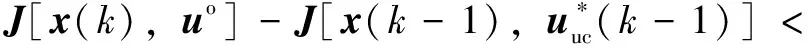
进一步，由公式(16)可得出：

[(),()]≤[(),]

因此，代价函数[(),()]单调递减，且当下述条件成立时，有[(∞),(∞)]=0：

()=[()]()-<0

(20)

可见，权重矩阵应满足式(20)。

2.2 改进的CCS-MPC设计方法

前述系统矩阵()实际上是随转速变化的，这意味着控制器式(17)中的加权矩阵必须通过在每个采样步中对公式(20)求解得出，计算量大。为降低计算成本，引入基于线性矩阵不等式(LMI)的方法。将公式(20)两边乘以,=，得出：

-[()]()>0

(21)

将上式转化为如下LMI：

(22)

设转速属于集合={∣≤≤}，由公式(3)和公式(10)可知，条件(22)关于是仿射的。因此，只需在集合的两个边界满足式(22)，即()>0且()>0。

如果IM具有较小的电阻，则磁通由具有较大时间常数=/的d轴电流产生。此时，可采用移动平均滤波器，使得磁通具有较低的变化频率。受文献[16]的启发，引入如下参考状态生成器：

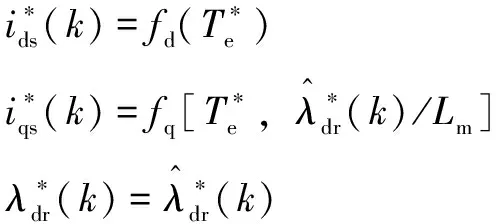
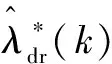
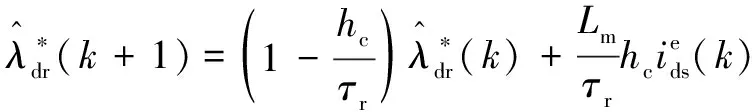
此时，公式(17)可修改为

(23)

其中：

式中：增益∈,可由下述过程确定：

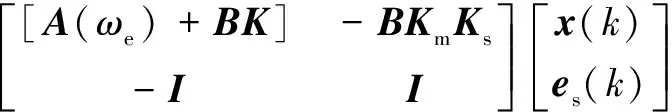
(24)

其中：=-(+)；=()。增益矩阵应使得齐次系统(24)具有稳定性。由公式(19)—式(24)可以得出，当满足如下不等式时，式(24)所示系统具有稳定性：

-[()]()>0

(25)

其中：=diag(,)(>0)且>=。因此，在收敛速度最大化的前提下，最优增益可以通过求解如下优化问题确定：

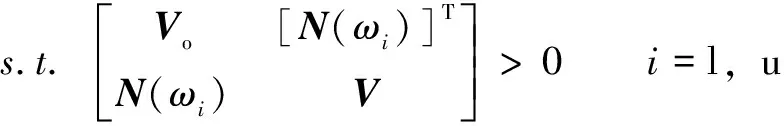
α>

(26)

式中：

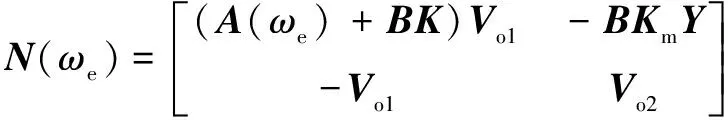
(27)

=

(28)

通过求解上述问题，可以得到最佳增益=()。上述优化问题本质上属于广义特征值问题，可以通过MATLAB2014a LMI工具箱YALMIP Solver进行求解。

3 转速控制器设计

不确定机械系统[式(4)]的离散时间模型可表示为

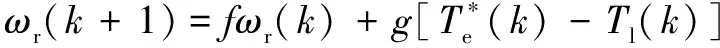
(29)

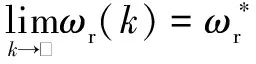
(30)

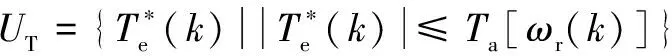
(31)

因此，首先基于无扰动名义模型(29)设计相应的稳定化MPC方法；针对不确定性扰动和转矩约束条件，设计相应的约束扰动观测器实现IM转速鲁棒控制。

3.1 基于名义模型的稳定化MPC方法

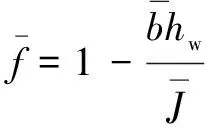
(32)

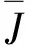
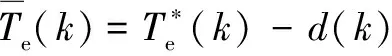
(33)

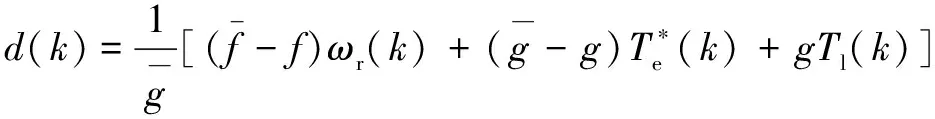
(34)

可见，()集总包含了模型参数及负载转矩的不确定性。

考虑稳态期望转速及其相应的输入参数，依据公式(32)，有：

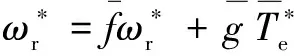
(35)

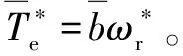
(36)

其中：

(37)

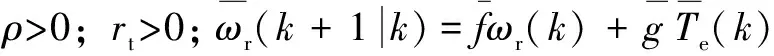
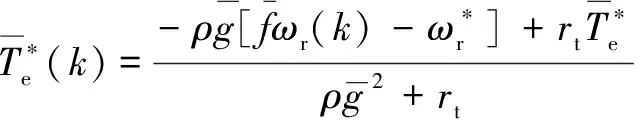
(38)

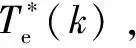
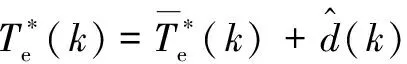
(39)

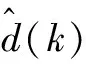
3.2 约束扰动观测器设计

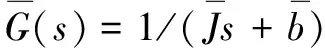
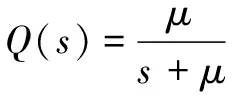
(40)

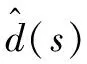
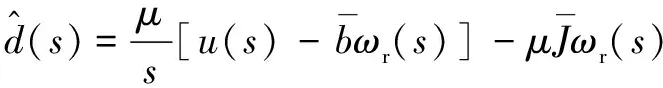
(41)

(42)

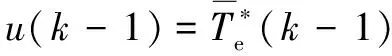
图2 基于经典DOB的鲁棒转速控制器

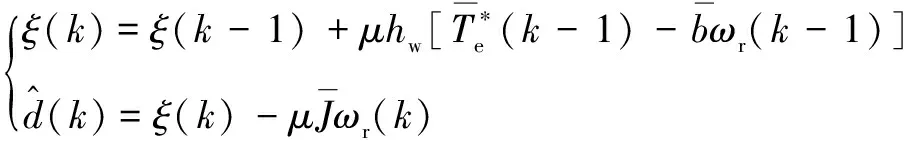
(43)

进而，闭环系统式(29)、(39)及(43)可表示为

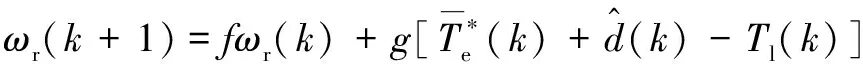
(44a)

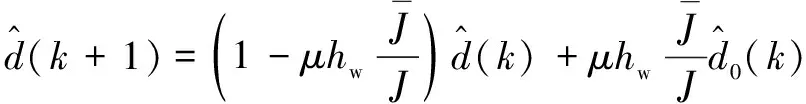
(44b)

其中：

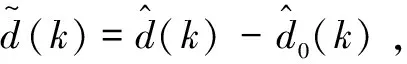
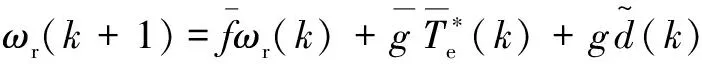
(45a)

(45b)

定理1：在假设1的条件下，如果满足如下两个不等式，则闭环系统式(45)具有稳定性。

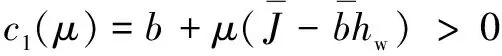
(46a)

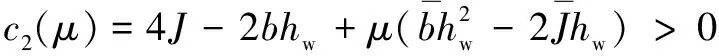
(46b)

证明：闭环系统的特征方程可以表示为

(47)

引入双线性变换=(+1)(-1)，将特征方程()变换至平面，称为()。对上述连续时间系统直接应用Routh稳定性判据，则当()>0且()>0时：

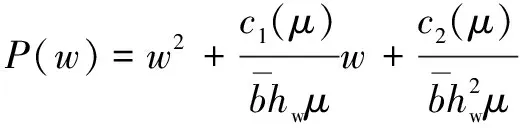
满足Herwitz稳定性条件，定理证毕。

为保证鲁棒稳定条件式(46)成立，应考虑不确定系统参数以及采样时间间隔的影响，可以通过假设较小的对问题进行简化，如推论1所述。

推论1：对于满足如下条件的

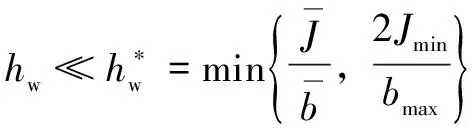
(48)

存在如下参数条件：

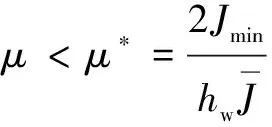
(49)

使得在假设1条件下，闭环系统式(29)及式(42)对于不确定性参数具有鲁棒性。

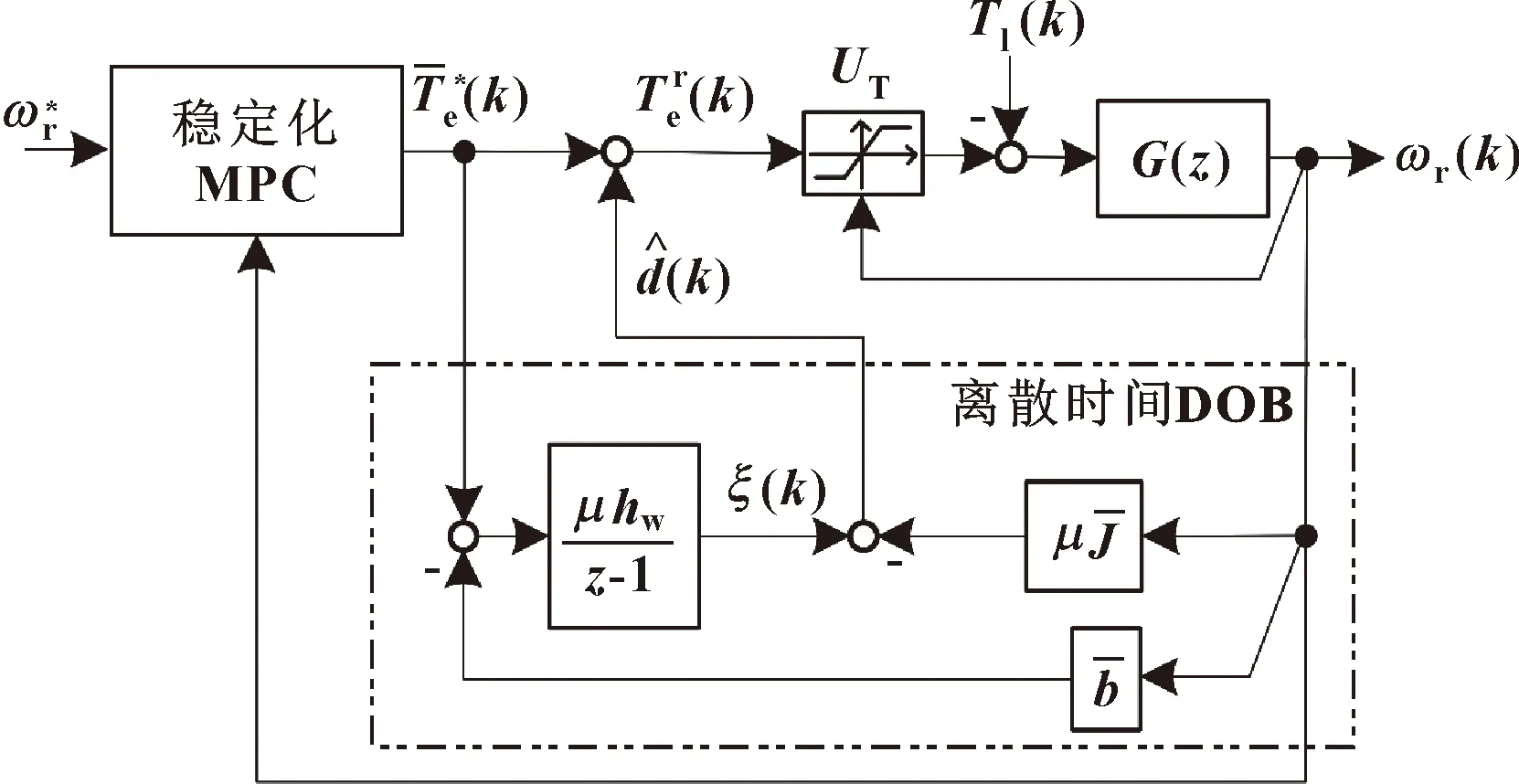
图3 基于稳定化MPC和离散时间DOB的鲁棒转速控制器

图4表示所提出的基于公式(50)所示的约束DOB的鲁棒速度控制器。为避免积分饱和问题，()的积分需满足如下约束：

图4 基于稳定化MPC和约束DOB的鲁棒转速控制器

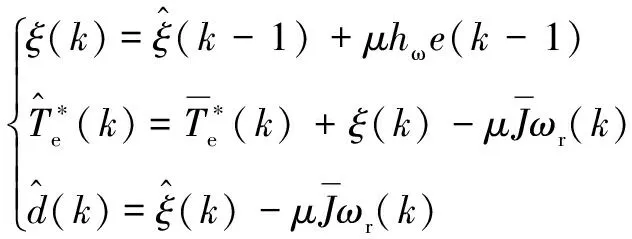
(50)

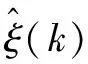
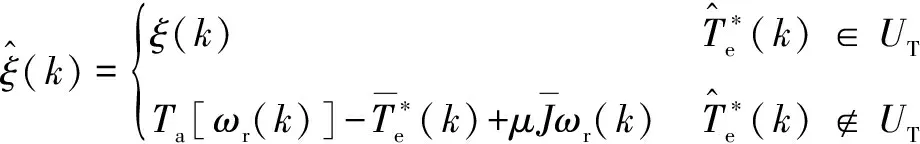
图4所示的鲁棒速度控制器控制流程如下：

(1)离线过程

①计算满足公式(20)的权重矩阵和公式(24)相应的增益及；

②求解式(36)所示的优化问题,获得式(23)所示积分器的增益。

(2)在线过程

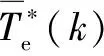
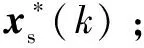
③依据式(16)和式(23)计算IM逆变器的控制输入()，并使用适当的PWM技术将()输入至逆变器。

4 实验验证

为验证所提出的控制方法，搭建相应的实验平台，如图5所示。实验采用两台相同的IM，其中一台为受控电机，用以验证所提出的控制方法，另一台则提供所需的负载转矩。所提出的控制算法由微处理器TMS320F28377D执行，逆变器的开关频率为=1/=10 kHz，并采用分辨率为12 800 PPR的光电编码器测量电机转速，采样间隔为10 ms。表1列出了所采用的IM各项参数。

图5 实验装置

表1 实验中IM的各项参数

为表述简洁，采用如下缩略语：

(1)CCS-MPC1：基于名义模型的稳定化MPC，如第2.1节所述；

(2)CCS-MPC2：所提出的改进CCS-MPC，参见第2.2节；

(3)DOB-MPC1：采用经典DOB的稳定化MPC；

(4)DOB-MPC2：所提出的采用约束DOB的稳定化MPC。

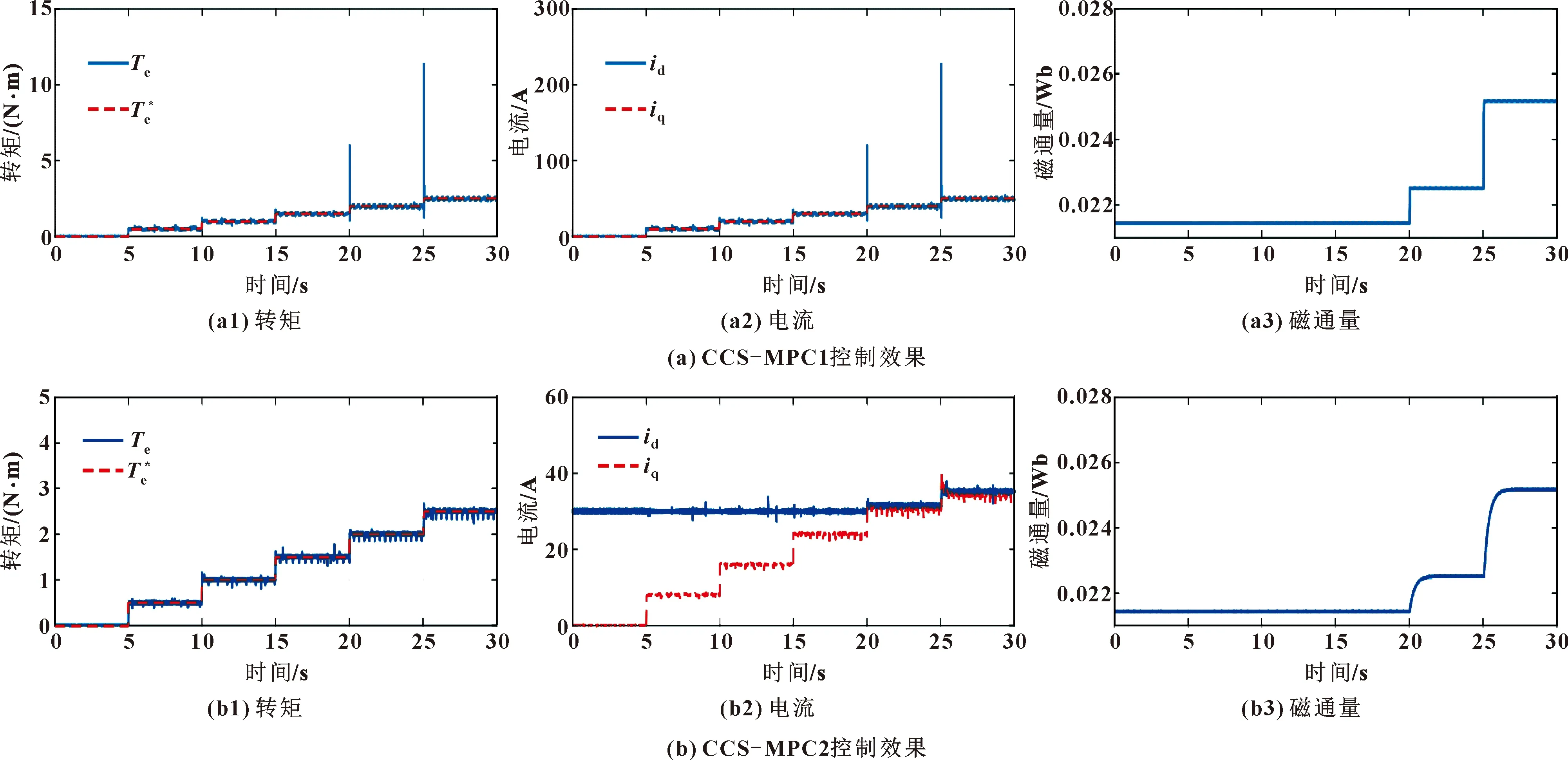
图6 步进信号下转矩控制器CCS-MPC1及CCS-MPC2的控制性能

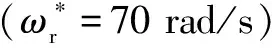
图7 阶跃参考转速下不同参数ρ对应的转速控制器DOB-MPC1及DOB-MPC2控制性能

图8 负载转矩扰动条件下的DOB-MPC2控制效果

5 结论

本文作者将模型预测方法与约束扰动观测器相结合，在考虑参数不确定性、负载扰动及转矩限制的基础上，提出一种感应电机的高性能鲁棒速度控制方法。基于串级控制结构，设计了相应的内环转矩控制器和外环鲁棒速度控制器。考虑系统参数随转速的变化，基于线性矩阵不等式提出改进的CCS-MPC方法进行内环转矩控制，在保证控制性能相同的前提下降低了计算成本。针对外环转速控制，设计一种DOB-MPC控制器，补偿了参数不确定性和负载转矩扰动的影响；同时，考虑电机转矩限制，利用条件积分器避免了积分饱和问题，通过给出相应的定理和推论，证明了所提速度控制器的稳定性及其条件。物理实验结果表明：与不考虑转矩限制的控制器相比，所提控制方法具有更好的瞬态响应，且系统在负载转矩扰动条件下具有优良的鲁棒性。