改进人工蜂群算法优化SVM的电能表故障诊断研究

韩彤，杨正宇 ,，陈叶 ，赵振刚

(1.云南电网有限责任公司电力科学研究院,云南昆明 650217;2.昆明理工大学信息工程与自动化学院,云南昆明 650500)

0 前言

电力系统的稳定运行依赖于各种电力设备，其中电能表是电力系统运行中的重要计量设备，用于测量用电量以及传输数据。随着电能表更新迭代越来越快，精密程度越来越高，其功能也更加多样化、模块化，倘若电能表故障得不到及时处理，将对电力系统稳定运行产生严重影响，因此准确快速识别电能表故障类型对维护电力系统正常运行、提高电表检修效率有重要意义。

目前主要采用的分类预测算法包括决策树、支持向量机、人工神经网络和随机森林等。文献[4]中利用模型自适应选择融合方法，通过分别取各类样本分类精度的最大值，计算样本精度阈值和差值，利用阈值和差值比较标记后选择融合模型，但是融合过程中计算过于繁琐，参量太多，计算工作量较大。文献[5]中利用排列熵(PE)具有抗噪能力强、计算效率高等优点，通过提取故障信号的MPE作为特征向量输入，将PSO与SVM结合起来建立模型，对SVM中参数进行优化选择，有着搜索速度快、效率高、算法简单的优点，但是对于离散的优化问题处理不佳，容易陷入局部最优。文献[6]中研究基于胶囊网络的诊断方法，特点是利用卷积神经网络强大的特征学习能力提取故障特征，建立特征和故障类型之间的映射关系，建立训练模型，结果表明诊断精度得到提高，但是编码过程过于复杂。文献[7]中充分分析特征与故障类型的相关性关系，基于实时数据与历史数据的SVM相关性分类方法实现判别，得到高精度判别模型，但是此模型需要大量数据进行支持，提高了系统运行的复杂性。黄帅等人利用PSO-LSSVM模型进行钢丝绳的故障诊断研究，相比于PSO-SVM速度明显提升，但是测试精度上没什么优势，而且相比之下不具有稀疏性。田干等人利用支持向量机回归(SVR)与最小二乘估计法相结合，建立了液体火箭发动机故障预测模型(LS-SVR),并分别将其应用于液体火箭发动机参数预测问题，但是分析选用的总样本数量较少，不具有很强的说服力。

人工蜂群(Artificial Bee Colony，ABC)算法是基于蜜蜂采蜜机制的蜂群算法，具有算法参数少、易于实现、稳定性好的优点。作者针对传统优化算法易于陷入局部最优的问题，利用Tent混沌搜索随机、遍历行的特点对ABC进行优化,有利于使其跳出局部最优解，通过不断优化支持向量机惩罚因子与核函数，提高了分类器的性能。通过实验仿真分析，验证了CABC-SVM在电能表故障诊断方面的优越性。

1 改进人工蜂群算法研究

1.1 人工蜂群算法原理

人工蜂群算法中，蜜蜂种类包含引领蜂、跟随蜂以及侦查蜂，蜜蜂对蜜源的搜索过程如下：(1)引领蜂负责发现蜜源，并记录蜜源信息；(2)跟随蜂通过识别引领蜂提供的蜜源信息，随机选择一个蜜源；(3)当一个蜜源被放弃后，相应的引领蜂变为侦查蜂，继续寻找新的蜜源。

在ABC算法过程中，蜜源的位置代表优化问题的可行解，蜜源的质量(适应度值)代表可行解的质量。首先，ABC算法随机生成含有个解的初始种群，每个解(=1,2,…,)用一个维向量=(1,2,…,)来表示，是待优化问题的特征参数的个数。初始解产生公式为

=+rand(0，1)(-)

(1)

其中：、分别为取值范围的上、下限;rand(0,1)为0～1之间的随机数。

跟随蜂根据得到的蜜源信息按照概率进行选择，质量越高的蜜源被选择的概率越大。引领蜂和跟随蜂按照下式搜索蜜源

(2)

其中:∈{1,2,…,},∈{1,2,…,}，和均为随机选取，但是≠；为[-1,1]间的随机数。

这里跟随蜂选择第个蜜源采蜜的概率为

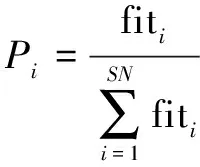
fit=()

(3)

式中:为第个蜜源(解)被选择的概率；fit为第个解的适应度值；()为适应度函数。

假定某个解未被更新的次数超过“limit”，则表示这个解连续经过有限次循环之后没有得到改善，认为这个解陷入局部最优，那么这个解就要考虑被放弃，与这个解相对应的引领蜂也转变为侦察蜂。计算公式如下

(4)

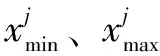
1.2 Tent混沌映射优化原理

Tent混沌映射(Chaos Optimization Algorithm)是利用混沌搜索的遍历性特点，使混沌算法在计算过程中可以不重复地经历一定范围状态，通过采用Tent映射模型系统产生混沌变量，并映射到相应取值区间进行混沌搜索。Tent混沌映射表达式如下

(5)

Tent混沌映射经贝努利变换后表达式如下

+1=(2)mod1

(6)

其中:表示(0,1)中随机数。

传统优化算法中，种群初始化的质量往往很大程度上决定着算法的寻优效果。在以往的研究内容中，通常采用随机初始化来产生相应的初始解，这种方法导致解空间的范围得不到充分的应用。通过Tent混沌映射初始化解，保证解在解空间内均匀分布。

在算法运算后期，各解运算结果相对较近，很难避免运算结果陷入局部最优，本文作者利用Tent混沌映射的思想，将所解蜜源利用Tent混沌搜索进行刷新，产生新一组混沌序列后代入算法内与现蜜源进行对比，保留最优适应度的解为最优解。

2 改进人工蜂群算法优化SVM模型建立

2.1 支持向量机

支持向量机(SVM)最初是为二值分类而设计的，原理思想是将特征映射到高维空间，在此高维空间内建立超平面，使得各特征向量距离次超平面距离最远，也就是此时分类误差越小。

文中电表故障一般属于多分类非线性问题，成对分类方法(One-Against-One)是在每两个类之间都构建一个二进制分类器，共构造(-1)/2个分类器，每个分类器根据两个类的数据进行训练，对于第类和第类数据，训练一个SVM即求解二次规划问题，给定含个样本的训练集=(,,…)(=1,2,…,)，其中为特征向量维数，(=1,2,…,)为标签类数。

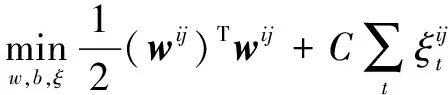
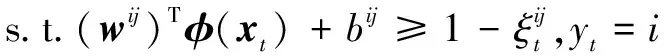
()()+≤-1,=

(7)

其中:上标表示是类和类之间SVM的参数；下标表示类和类的并集中样本的索引；()表示输入空间到特征空间的非线性映射。

第类和第类之间SVM决策函数为

()=sign[()()+]

(8)

径向基核函数RBF是常用的核函数，其函数表达式为

(，)=exp(-‖-‖)

>0

(9)

2.2 基于改进人工蜂群算法优化SVM模型

针对改进人工蜂群算法优化SVM对电表故障分类问题，包括数据预处理、Tent混沌映射优化初始蜂群、SVM利用优化参数分类等过程，具体步骤如下：

(1)对获取数据进行预处理，并对数据进行归一化。

(2)设定算法初始值，包括种群数量，蜜源数量，更新限制次数limit，最大迭代次数，参数、取值范围。

(3)以Tent混沌映射产生初始解，引领蜂根据式(2)进行领域搜索，以贪婪法选择较好蜜源，以式(3)计算蜜源被跟随蜂选择的概率。

(4)跟随蜂根据式(2)搜索选择的蜜源，计算适应度值。

(5)若有蜜源(解)经limit次循环后没有改善，将蜜源通过Tent混沌搜索产生新的蜜源来替代，计算其适应度值，保留最优解。

(5)达到最大迭代次数后，将最优解赋值于SVM模型。

(7)利用数据集划分训练集以及测试集，测试集代入通过最优、训练好的模型，输出分类结果。

改进人工蜂群算法优化SVM方法流程如图1所示。

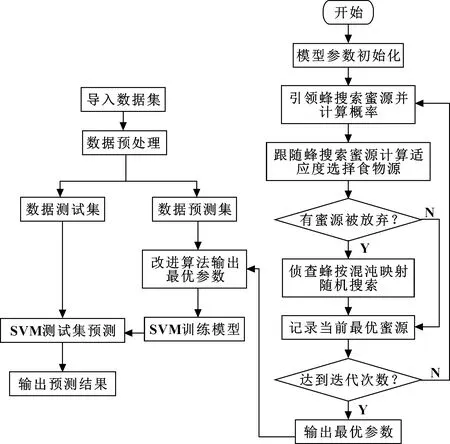
图1 模型整体流程

3 算例分析

3.1 样本数据整理

根据云南电网某公司监测到的电能表故障数据，以8∶2的比例划分训练集以及测试集。由于各影响特征之间数值范围相差较大，为了避免系统精度低或损失函数不收敛等问题，对数据进行归一化处理，采用Min-Max标准化将其归化至(0,1)区间内。计算公式如下

(10)

对不同故障类别编号，由于终端上电、掉电等故障类型采集不到有效数据，所以先不予以讨论。经数据研究整理，反映电能表故障的因素包括A相电压、B相电压、C相电压、A相电流、B相电流、C相电流以及正向有功总功能。电能表故障类型与数据集样本关系如表1所示，对优化算法设置初值，CABC-SVM各参数设定如表2所示。

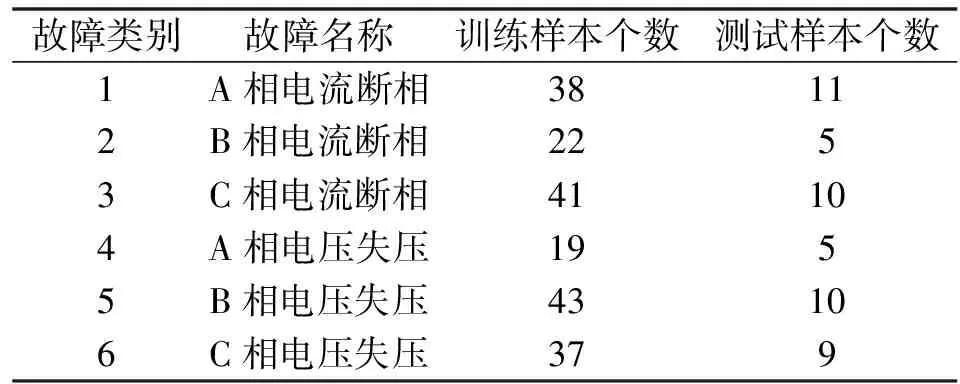
表1 故障编号以及样本信息

表2 系统初始化参数

3.2 实验结果分析

为了验证提出的CABC-SVM模型的有效性，对建立的CABC-SVM优化模型进行仿真实验，利用MATLAB软件建模和进行仿真实验。图2所示为系统迭代次数与适应度函数值的关系。

图2 系统迭代次数与适应度函数值的关系

由图2可知：随着迭代次数的增加，当前解通过不断更新获得更优的适应度函数值，逐渐向最优解逼近。为了更好地体现出CABC-SVM的分类效果，引入ABC-SVM、PSO-SVM以及GA-SVM模型做分类效果对比。相比于上面3种模型，在算法中期CABC-SVM明显具有更好跳出局部最优解的能力，获得更优适应度并且CABC-SVM在第40代就完全收敛，而ABC-SVM、GA-SVM、PSO-SVM分别在89、70和79代才收敛，对比发现CABC-SVM模型具有更好的收敛能力。图3为4种模型对测试集分类精度的情况。

如图3所示:以50组数据作为测试数据进行分类，CABC-SVM出现了1个诊断错误，诊断精度达到98.0%;ABC-SVM在和CABC-SVM模型精度相同但运行时间更长；PSO-SVM与GA-SVM模型分别有3个和5个诊断错误，诊断精度分别为94.0%和90.0%。表3为各模型性能对比。

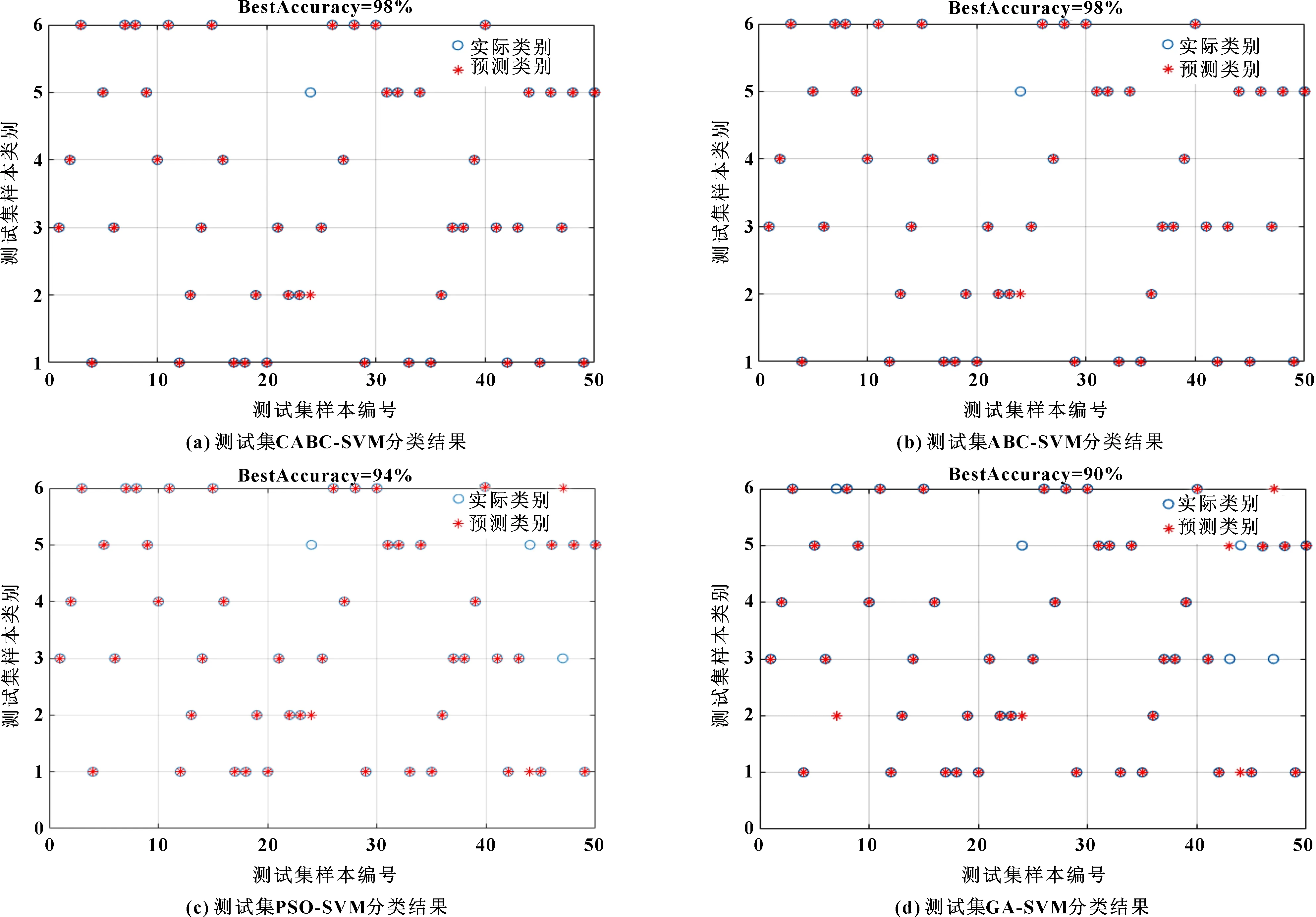
图3 CABC-SVM、ABC-SVM、PSO-SVM和GA-SVM分类模型分类精度对比

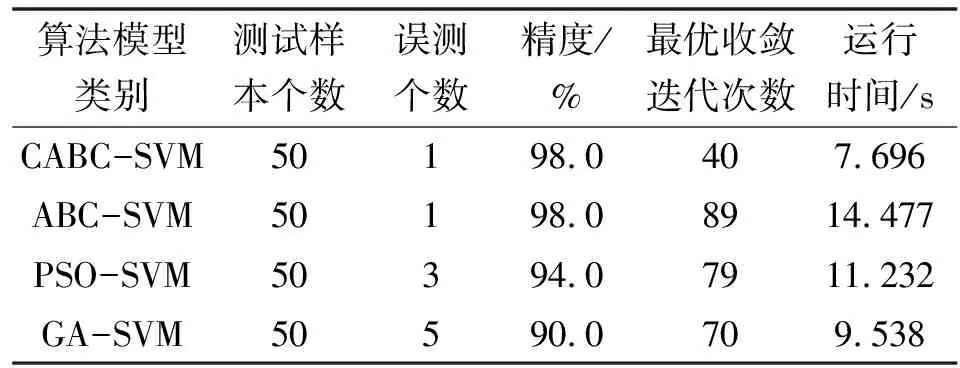
表3 各模型性能对比

经MATLAB建模仿真分析发现无论在精度以及收敛迭代次数和运行时间上，CABC-SVM模型都具有一定优势，尤其与传统ABC-SVM算法相比运行时间缩短接近一倍。

4 结束语

提出一种基于改进人工蜂群算法优化SVM的电能表故障诊断方法，通过分析故障数据的类型和规模，对数据进行预处理；利用改进人工蜂群算法对SVM分类器的惩罚因子和核函数参数进行优化；最后将故障训练集作为输入建立模型，测试集验证模型性能；通过实验仿真分析，对比文中4类模型对于故障数据的分类效果，证实了CABC-SVM在电能表故障诊断方面具有快速收敛、高精度的诊断效果，为电能表故障诊断提供了一种参考。