一种求解三维简约布里渊区体积的方法
李建军,张振东
(北京工业大学 电子科学与技术学院,北京 100124)
布里渊区(BZ,Brillouin Zone)是固体物理学中的一个非常重要的概念,在晶格振动及能带论等与波相关的章节都有涉及[1,2]. BZ定义为波矢空间的点的集合,三维情况下,BZ是由倒格矢的垂直平分面围成的区域. 根据从原点到各布里渊区需穿越垂直平分面的数目,划分为第一BZ(不穿过任何垂直平分面),第二BZ(穿过1个垂直平分面),以及第N个BZ(穿过N-1个垂直平分面)[3]. 不论是能带论中的E-k关系,还是晶格振动中ω-q关系,都具有关于倒格矢的平移对称性,因此可以通过平移将E-k或ω-q关系约化在第一BZ内表示,因此第一BZ也叫简约布里渊区,通常所说的BZ一般是指简约布里渊区.
BZ的一个重要性质是所有BZ的体积都相等,且等于倒格子原胞的体积[4]. 对于不同的晶体结构,由于倒格子形式不同,因此简约BZ的形状也不同. 当前,为了具体计算简约BZ区的体积以体现其等于倒格子原胞的体积,需要针对不同的简约BZ形状采用不同的方法求解其体积,即使是求解同一种BZ的体积,也有不同的方法[5-8]. 这就增加了本知识点的教和学的难度. 据此,本文根据简约BZ的结构特点,提出一种可求解各种形状BZ体积的普适方法,此方法简单且易于掌握.
1 简约BZ体积的求解
简约BZ是由距k空间原点Γ最近或次近的倒格点的连线的垂直平分面围成的凸多面体,因此Γ点位于该多面体内部. 设凸表平面的数目为N,从Γ点到多面体的各顶点做连线,则凸多面体被划分成为N个以Γ为顶点的棱锥,简约BZ的体积V便是这N个棱锥体积的和,即
(1)
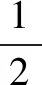
(2)

图1 面心立方简约布里渊区的体积的求解

(3)
式(3)中,利用了两个矢量叉乘的模等于其围建的平行四边形的面积这一性质,将式(3)代入式(2),得
(4)

(5)
将式(5)代入式(1),即得到求解BZ体积的普适公式为
(6)
由式(6)可见,不论是哪种形式的布里渊区,只要确定出其表面各顶点的坐标以及与各表面相对应的倒格矢,即可求得其体积.
归纳用式(6)求解BZ体积的具体过程如下:① 从原点Γ向有N个表平面的BZ的各顶点做直线,以各直线为棱边将BZ划分为以Γ为共同顶点的N个棱锥体;② 写出以各棱锥底面为垂直平分面的倒格矢Gn;③ 写出棱锥底面各顶点的坐标An,m;④ 由式(5)求各棱锥的体积;⑤ 由式(6)对各棱锥的体积求和得到BZ的体积.
2 应用实例
下面首先以面心立方正格子为例,给出应用实例. 对于面心立方的正格子,其固体物理学原胞的基矢为
(7)
其中,a是晶格常量,i、j、k是直角坐标系3个方向的单位矢量. 根据正、倒格子基矢间的关系,求得倒格子基矢为
(8)
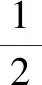
面心立方的简约BZ是由体心立方8个顶角的最近邻倒格矢及6个次近邻倒格矢的垂直平分面围成的14面体,如图1(a)所示.14个面中的8个面是正六边形,6个面是正四边形.从原点Γ向各面的顶点引直线作为棱边,由于简约BZ的对称性,简约BZ被划分为8个体积相同的正六棱锥和6个体积相同的正四棱锥.
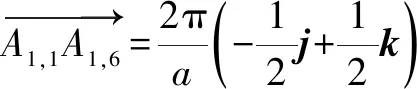
(9)
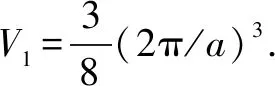
最后,把8个六棱锥与6个四棱锥的体积求和,得简约BZ的体积为4(2π/a)3,与前述倒格子原胞的体积相等.
对于正格子为体心立方的晶体结构,其固体物理学原胞的基矢为


(10)
根据正、倒格子基矢间的关系,求得体心立方的倒格子基矢为
(11)


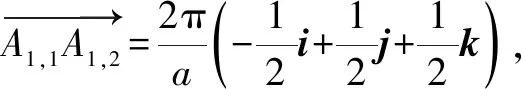
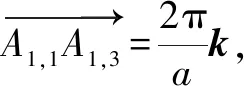
(12)
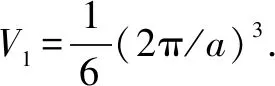
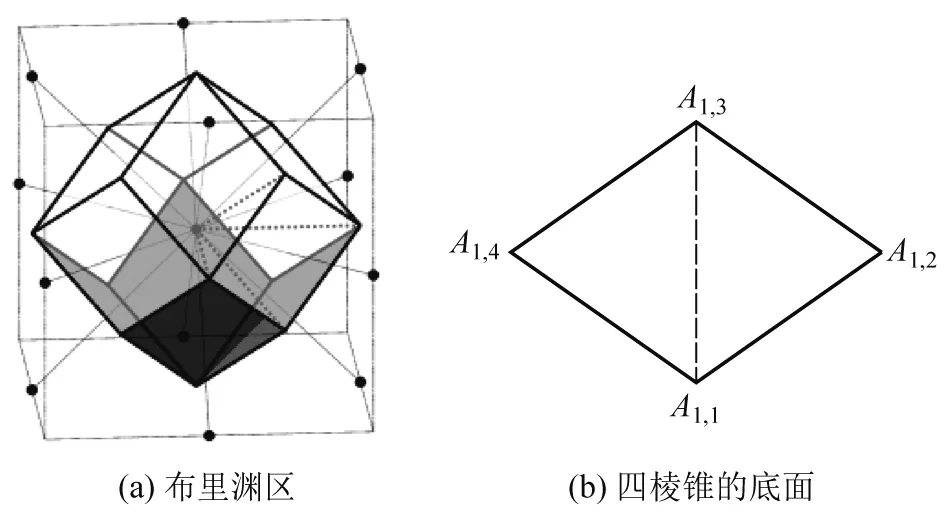
图2 体心立方简约布里渊区体积的求解
3 结语
为求解BZ的体积,可将其离散为以原点Γ为共同顶点的N个棱锥体来求解. 此方法简单直观、易于掌握,且适于求解任意晶体结构的BZ区体积. 布里渊区是固体物理学的一个重要概念,本文提出的BZ体积的求解方法对该知识点的教与学提供了有益的手段.

