二体问题的探讨

林灏宸, 马 丽

(西安理工大学 理学院，陕西 西安 710048)

想必大家都听说过刘慈欣先生写的科幻小说《三体》，距离地球四光年外的“三体文明”，在3颗无规则运行的恒星主导下，经历百余次毁灭与重生，被逼迫不得不逃离母星. 在探索宇宙的过程中，我们希望能定量地精确计算出各天体的轨道，这免不了牵涉多天体的相互作用. 对于多体问题，人们目前还不能完全解决，只能通过数值积分方法(如Runge-Kutta法、几何积分算法、显式辛算法、Nacozy流形改正方法、Fukushima旋转线性变换方法等)进行轨道演化计算[1].

对于太阳系这种含1个占绝大部分质量的主天体的特殊N体问题，太阳与每个行星组成的二体会受到其余星体的引力作用(受摄二体模型). 当摄动力远小于二体间相互作用力时，在不需要精确计算的情况下，可将该多体问题简化为二体问题.

本文主要是对这一类二体问题的方法进行总结，通过变换参考系和能量守恒两个角度推导出了柯尼希定理，并引入折合质量μ，简化了二体问题的讨论. 同时介绍了等效一体化处理问题的方法，用折合质量进行二体修正的本质是将问题一体化处理.

1 柯尼希定理

我们在高中就已经接触到碰撞问题，想必大家都见过一道很经典的问题，就是在两个物块之间加一个弹簧，在它们运动的过程中，求解两物块之间的弹性势能. 我们可以通过列弹簧处于原长和两物块共速两时刻的动量守恒、能量守恒，联立，进而求解，但求解过程很繁琐. 如果运用柯尼希定理就会简便很多，甚至可以口算得出答案. 这样的二体问题的例子还有很多[2-4].下面先给出柯尼希定理的证明.

证明：设两质点质量分别为m1、m2，相对于地面参考系S和平动质心系S′的速度分别为v1、v2；v′1、v′2,u为质点1相对质点2的相对速度，有

u=v12=v1-v2=v′1-v′2

(1)

m1v′1+m2v′2=0

(2)

由方程组可得

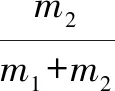
(3)

(4)

可得相对于质心系S′的动能E′k的表达式为

(5)

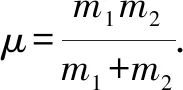
我们还可以从能量守恒的角度验证柯尼希定理的正确性：

质心速度为

(6)

相对于质心系S′的动能为

E′k=Ek-Ekc=

(7)

2 二体问题与等效一体化思路

运用折合质量对二体问题进行修正的方法如下, 即选定一个随质点1运动的参考系，在该参考系上看质点1为静质点，另一个质点2为动质点，同时认为该静质点1所在的参考系为惯性系，写出动质点相对于静质点的动力学方程F=ma，把ma中的动质点质量m改为折合质量μ，即可实现对二体问题求解的简化.

等效一体化就是将需要考虑的一系列物体视为整个系统，通过讨论系统中各物体之间的联系，或者寻找出系统中保持不变的点或参数，选取其为基准，来对实际问题进行求解.

在二体问题中，引入折合质量进行二体修正的本质是找出两质点间的相互联系，将问题一体化处理.同时我们也可以选用质心参考系来对两个质点的运动情况进行研究.

二体问题中质点1、质点2和质心C始终在同一条直线上，该质心系为惯性系.设质量为m1的质点1相对于质心C的位矢为r1c，质量为m2的质点2相对于质心C的位矢为r2c，如图1所示，有

(8)

(9)

求导可得

(10)

(11)

(12)

(13)

所以有

(14)

m1a1c=f12

(15)

m2a2c=-f12=f21

(16)

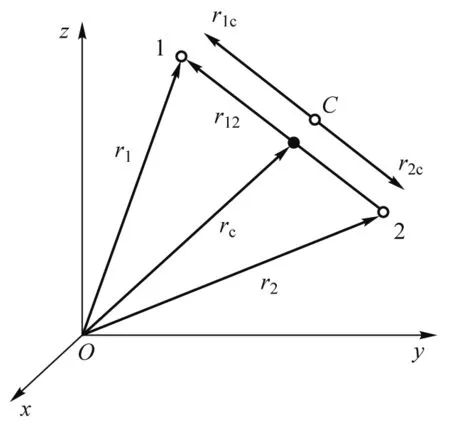
图1 等效一体化示意图

综上所述，对两质点孤立系统的问题简化处理，可以找出两质点间相互联系，采用折合质量的方法进行修正，也可以选定质心系，写出两质点相对于质心的动力学方程，进而求解.

3 二体问题多解法的讨论与改进

在许多天体问题中需要计算两个天体相碰的时间，一般都采用积分的方法进行求解，计算量相对来说比较大.在两个天体相对静止或者速度相差不大的情况下，可以利用开普勒第三定律和退化椭圆的方法，简便快速地求解二者相碰所需时间.

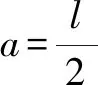
这里必须强调的是，该方法只适用于求解末状态的时间，如需具体求出相距某一距离的时间仍需要通过积分法进行求解.

3.1 天体系统

假设宇宙空间的一个惯性系中，有两颗相距为d，质量分别为m1、m2的静止不动的星球，在万有引力的相互作用下，开始相向运动，dm1和dm2为m1、m2相对于质心C点的距离,如图2所示.求两星球由静止到相碰，共经历多长时间？设两星球半径远比相互间距小[5].

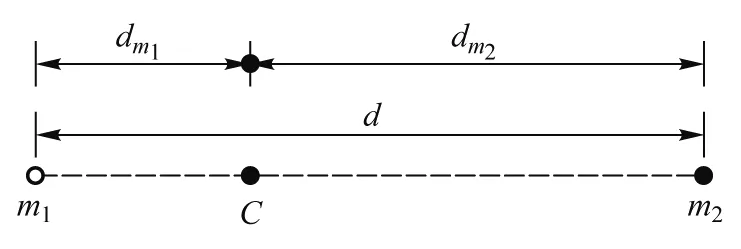
图2 两个天体组成的系统示意图

对本问题，我们分别采用折合质量进行二体修正法、质心等效质量法进行求解.

方法一：用折合质量进行二体修正法

商务英语有着很重要的作用，尤其是在我国农产品对外贸易中，其以独特的专业性特点为农产品对外贸易领域奠定了坚实基础，如今在农产品对外贸易中，商务英语应用占很大比重。商务英语在农产品对外贸易进行协商和谈判时，可以帮助贸易双方简单直白地了解合作意向。由此可见，商务英语在我国和其他国家的贸易中起着非常重要的作用。

选任意质点为静质点，比如我们选m1为静质点，写出动质点m2的动力学方程

(17)

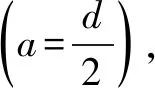
(18)

方法二：质心等效质量法

在质心系中引入质心质量等效替代某一质点质量，讨论质心与待研究质点的受力情况.

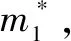
(19)

(20)

(21)

这两种方法本质相差不大，求解的步骤都比较简略.

3.2 点电荷系统

对于电磁学中两个静止异号点电荷的运动情况，在一些书籍中都只有积分解法，求解过程过于繁琐，如果我们并不需要求出两个点电荷相距某一距离的时间，就没有必要采用微积分，只需要类比之前讨论的天体系统的二体问题就可以更简洁地求解.

下面讨论如何类比天体问题，快速求出两个点电荷从相对静止的初状态到最后相碰所经历的时间.

真空中有两个异号点电荷q1和q2，它们的质量分别为m1和m2，t=0时刻，两个电荷均静止，相距r0，如图3所示.试问它们何时相碰，只考虑其间的库仑相互作用[6].

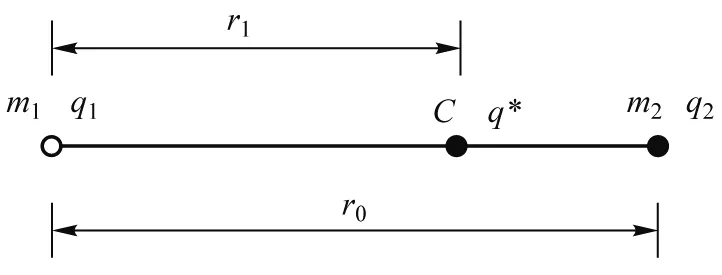
图3 两个点电荷组成的系统示意图

对本问题，我们先采用常规积分法进行计算，再通过类比上述的天体系统二体问题，采用折合质量进行二体修正法，以及质心等效电荷量法对问题进行处理.

方法一：常规积分法

(22)

(23)

(24)

(25)

(26)

(27)

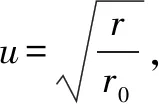
dr=2r0udu,

(28)

代入式(27)，得

(29)

两点电荷相碰时r=0，有

(30)

方法二：用折合质量进行二体修正法

我们可以把它类比天体问题，选取任意点电荷为静质点，比如选m2为静质点，m1为动质点.由于在这道题中只考虑两电荷之间的库仑力，就相当于天体中二体间的万有引力在这里变成了两点电荷间的库仑力，同样都是平方反比的力，在系统总能量E<0时二者相对位置满足椭圆轨迹，类比二体天体问题可列出动力学方程：

(31)

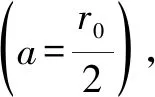
(32)

方法三：质心等效电荷量法

在质心系中引入质心电荷量等效替代某一点电荷所带电荷量，讨论质心与待研究点电荷的受力情况.

选取质心C为参考点，m1和m2最终在质心处相碰，某一点电荷受另一点电荷的作用力可等效为位于质心处的点电荷对其施加的库仑力，我们只需求出在质心C处的等效电荷量q*，即可通过退化椭圆的方法求出相碰时间.

m1到C点的距离为r1：

(33)

等效电荷为q*：

(34)

(35)

类比二体天体问题得动力学方程：

(36)

相碰时间为t：

(37)

可以看到，采用常规的积分法求解过程非常繁琐，而采用本论文提出的二体修正法以及质心等效法要简略很多.所以在二体问题中运用等效一体化思路，找出两质点间的相互联系，通过引入折合质量进行二体修正，或者采用等效替代的思维，选用质心参考系来对两个质点的运动情况进行研究，在很大程度上可以简化二体问题的求解.

4 总结

本文对二体问题的求解方法进行了归纳总结，给出了相关的证明，提出等效一体化的思路，简化了二体问题的讨论.并引入了退化椭圆求时间的方法巧解了两物体在平方反比的作用力下从相对静止到碰撞的时间问题.在本文的最后，对二体问题的多解法进行了讨论与改进，同时用天体系统二体问题的结论类比两个点电荷问题，避免书中积分的繁琐，突出了对问题等效一体化处理的优越性.