量子力学中表象变换理论的教学探讨：结合中微子振荡的前沿案例

涂 涛，郭奥林，李传锋，郭光灿

(中国科学技术大学 物理学院，中国科学院量子信息重点实验室，安徽 合肥 230026)

量子力学是物理学专业一门重要的基础课程，同时其内容又与量子调控、量子信息、粒子物理、凝聚态物理等领域的研究前沿密切联系在一起[1-3]. 如何把现代物理学的一些前沿进展，与基础物理课程的教学内容融合在一起，需要在教学研究、教学改革和课程建设中不断思考、探索与实践.

在目前的量子力学教材中[4-7]，有一些基本概念和知识点如定态薛定谔方程，有许多具体的教学案例和教学研究，例如结合无限深方势阱、中心势场中的氢原子等来求解定态薛定谔方程[8-11]. 然而，还有一些基本概念和知识点如表象变换理论等，都比较抽象，也没有具体的教学案例. 学生们普遍反映这些概念和知识点较难理解，也不清楚这些抽象公式所代表的物理图像. 因此表象变换理论等内容成为当前量子力学教学中的重难点之一.

笔者所在的中国科学技术大学量子力学教学研究团队，从2006年起就提出 “面向现代物理前沿，开展科教融合的量子力学课程建设”.团队持续关注物理学研究前沿和动态，探索将一些前沿进展以适合本科生教学的方式融入到量子力学课程中[12,13]. 一方面，学生运用学到的基础知识来解决具体和实际的科研问题，可以大大加深他们对基础知识的理解和掌握. 另一方面，研究前沿作为教学案例，也是学生接触科学研究的一条途径，可以很好地激发他们从事科学研究的兴趣和热情. 本文主要探讨利用中微子振荡作为教学案例促进量子力学中表象变换理论的教学过程和效果.

1 表象变换理论教学的难点分析

|Ψ〉=∑iai|vi〉

(1)

这里展开系数是ai.

|Ψ〉=∑jbj|φj〉

(2)

这里展开系数是bj.

同样一个量子态，可以分别用A表象和B表象来表示:

|Ψ〉=∑iai|vi〉=∑jbj|φj〉

(3)

对于上式，左乘以A表象的基矢〈vi|，利用基矢的正交归一性，可以得到

ai=∑j〈vi|φj〉bj=∑jSijbj

(4)

可以把上式写成矩阵的形式，即为

(5)

式(5)表明，同一个量子态在A表象和B表象中的表示系数是有联系的，它们通过一个幺正矩阵S联系在一起.

以上就是量子力学中表象变换理论的一般形式. 在我们多年的教学实践中[13]，通过对学生学习情况的问卷调查和交流讨论，学生普遍反映存在如下两个困难：1) 这些矩阵公式比较抽象，学生往往不知道如何将抽象的符号与具体的物理图像联系在一起；2) 这些公式包含的概念较多，有表象、力学量算符、态矢量、本征态的正交归一性和完备性等，如何用一个完整的物理图像来理解这么多的公式，也有相当大的挑战.

针对上述困难，我们选取中微子振荡这一粒子物理学前沿作为教学案例，促进学生对表象变换理论的学习和理解.

2 中微子物理前沿进展的介绍和引入

为了能够将中微子振荡作为教学案例，我们需要向学生简单地介绍一下中微子物理. 这部分内容可以看作是原子物理课程中粒子物理内容的一些扩展和延伸，学生不难掌握.

中微子是构成物质世界的一种基本粒子，中微子不带电，只参与弱相互作用，所以它与其他物质的相互作用很弱. 为了探测到中微子，需要有很强的中微子源，也需要庞大的探测器，才能产生足够的信号. 历史上，美国科学家利用核反应堆发射中微子束流，并利用200 L的水和1 682 L的液体闪烁体作为探测器，测量到了中微子的信号. 中微子的发现获得了1988年和1995年两次诺贝尔物理学奖.

目前科学家已经发现了3种类型的中微子，分别是电子中微子、μ子中微子和τ子中微子. 日本科学家在KamLand建造了埋在地下矿井中的、拥有50 000 t水和11 500个光电倍增管的大型中微子探测装置. 他们分别探测了来自核反应堆的中微子束流，和由宇宙射线产生的中微子束流. 他们观测到如下有趣的现象：

核反应堆会产生一定数目的电子中微子，当这些电子中微子经过一段距离，到达KamLand的探测器时，科学家观测到电子中微子数目出现减少.

当高能宇宙射线进入大气层，会产生一定数量的电子中微子和μ子中微子. 当这些电子中微子和μ子中微子经过一段距离达到KamLand的探测器时，科学家观测到电子中微子的数目几乎不变，而μ子中微子数目发生减少.

这些现象说明了中微子会在几种不同状态之间发生相互转换，称为中微子振荡. 中微子振荡是粒子物理学的研究前沿，这一发现已经获得了2002年和2015年两次诺贝尔物理学奖，进一步的研究仍然方兴未艾[14,15].

下面我们就利用量子力学的表象变换理论来解释中微子振荡这一有趣而重要的现象.

3 两代中微子情况的表象变换理论

3.1 中微子的味表象

在味表象中，中微子的一般状态可以表示为这两种基矢的叠加：

(6)

这一组数a1、a2就构成了量子态在味表象中的表示.

3.2 味表象中的力学量算符

在味表象中，中微子的质量算符可以表示为一个矩阵：

(7)

这个矩阵表示的物理意义是：对角元素mee、mμμ分别表示电子中微子和μ子中微子的质量.而非对角元素meμ、mμe表示电子中微子和μ子中微子之间的混合.

首先，我们求解质量算符的本征方程：

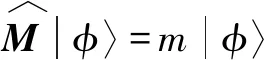
(8)

此时它是一个矩阵的本征方程:

(9)

这是一个矩阵的本征问题.质量本征值可以由如下方程得到：

(10)

通过代数运算，可以求得两个质量本征值为

(11)

这里我们令meμ=mμe.

进一步，我们将质量本征值代入方程(9)中，可以得到相应的两个质量本征态为

(12)

3.3 中微子的质量表象

通过线性代数计算，我们可以验证如下式子：

即质量本征态|φ1〉和|φ2〉是正交归一的，因此它们构成态空间的一组基矢.以|φ1〉和|φ2〉为基矢的表象，我们称为质量表象.

在质量表象中，中微子的某一状态可以表示为质量本征态的叠加：

(13)

这一组数b1、b2就构成量子态在质量表象中的表示.

3.4 中微子两个表象之间的表象变换

从上面的讨论中，我们看到，同样一个中微子状态在味表象和质量表象中，可以表示为不同的形式，分别是表达式(6)和(13).一个很自然的问题是，这两种表示之间有什么联系呢？

注意到，同一个中微子态有

|Ψ〉=a1|ve〉+a2|vμ〉=b1|φ1〉+b2|φ2〉

(14)

对于上式，左乘〈ve|，我们有

〈ve|ve〉a1+〈ve|vμ〉a2=〈ve|φ1〉b1+〈ve|φ2〉b2

(15)

再利用基矢的正交归一性，可得到如下关系式：

a1=〈ve|φ1〉b1+〈ve|φ2〉b2

(16)

同理，对式(9)，如果左乘〈vμ|，可得到类似关系式：

a2=〈vμ|φ1〉b1+〈vμ|φ2〉b2

(17)

为更清楚，将式(16)和(17)表示为矩阵的形式：

(18)

式(18)清楚的显示，同一个量子态在味表象和质量表象这两个表象中的不同表示之间是相互关联的，它们是通过一个变换矩阵S联系在一起的.矩阵元素Sij是味表象的基矢|vi〉和质量表象的基矢|φj〉之间的标积Sij=〈vi|φj〉.

在3.2节中，我们已经求得了在味表象下，质量本征态的表达式(12)，因此不难得到如下结果：

这样我们可以把表象变换矩阵S写成

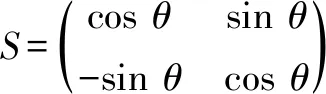
(19)

表象变换矩阵S具有很直观的物理意义，每个矩阵元Sij代表了电子中微子态|ve〉或μ子中微子态|vμ〉是由两种质量本征态|φ1〉和|φ2〉混合而成的

|ve〉=cosθ|φ1〉+sinθ|φ2〉=S11|φ1〉+S12|φ2〉

(20)

|vμ〉=-sinθ|φ1〉+cosθ|φ2〉=S21|φ1〉+S22|φ2〉

(21)

这里，我们把θ称为中微子的混合角.如果用表象变换矩阵S表示，即为

|vi〉=∑jSij|φj〉

(22)

3.5 中微子的含时演化和中微子振荡现象

下面，利用中微子的表象变换理论，分析中微子状态的含时演化行为.设在初始时刻，产生了一个电子中微子，在味表象下，中微子的状态表示为

|Ψ(0)〉=|ve〉

(23)

利用味表象和质量表象之间的变换关系，可以得到在质量表象下的式子：

|Ψ(0)〉=cosθ|φ1〉+sinθ|φ2〉

(24)

显然，中微子的状态可以看成是两种质量本征态|φ1〉和|φ2〉的组合.

(25)

因为每种质量的中微子都随着其能量发生含时演化，所以我们可以得到t时刻的状态为

|Ψ(t)〉=cosθe-iE1t/ћ|φ1〉+sinθe-iE2t/ћ|φ2〉

(26)

这里的E1和E2分别代表两种质量为m1和m2的中微子相应的能量.

因为在实验中，我们探测的是电子中微子或μ子中微子的信号，所以我们重新在味表象下表示t时刻的状态.利用味表象和质量表象之间的变换关系，我们可以得到

|Ψ(t)〉=(cos2θe-iE1t/ћ+sin2θe-iE2t/ћ)|ve〉+

sinθcosθ(e-iE2t/ћ-e-iE1t/ћ)|vμ〉

(27)

从上述表达式，我们容易得到，在t时刻发现中微子处于电子中微子状态|ve〉的概率为

Pe(t)=|ve|Ψ(t)〉|2=

|cos2θe-iE1t/ћ+sin2θe-iE2t/ћ|2=

1-sin22θsin2[ΔEt/2ћ]

(28)

这里我们令ΔE=E1-E2.

(29)

这里定义中微子从发射源到探测器的飞行距离为L.

上述理论公式(29)清楚的表明，初始时候的电子中微子，在t时刻只有一部分的概率Pe仍然处在电子中微子，另外有1-Pe的概率转化为μ子中微子.这种随时间演化的现象称为中微子振荡.而中微子振荡的概率取决于两个关键的参数：混合角θ和质量差Δm.

3.6 与中微子实验的对照和分析

科学家使用核反应堆产生电子中微子，然后在距离为L处利用探测器探测到达的电子中微子. 世界上许多发达国家都开展了这类中微子振荡的实验，特别是日本的KamLand实验组. 这些反应堆中微子的实验结果[14]，在图1中由不同形状的数据点给出. 在图1中，横轴表示中微子从反应堆到探测器的飞行距离L，纵轴表示探测器测量到电子中微子的概率Pe.

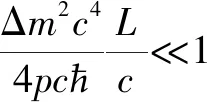
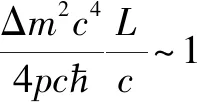
进一步，可以利用理论公式(29)来定量分析日本KamLand组的实验结果. 在KamLand组的实验中，反应堆产生的中微子动量为pc=4 Mev，从反应堆到探测器的距离为L=180 km.两个主要参数的数值为：中微子的混合角θ=0.59，中微子的质量差Δm2c4=7.1×10-5eV2.将这些参数代入理论公式(29)，我们可以计算最后探测到电子中微子的概率为Pe=0.47，这与实验测量值Pe=0.51是符合的[14].

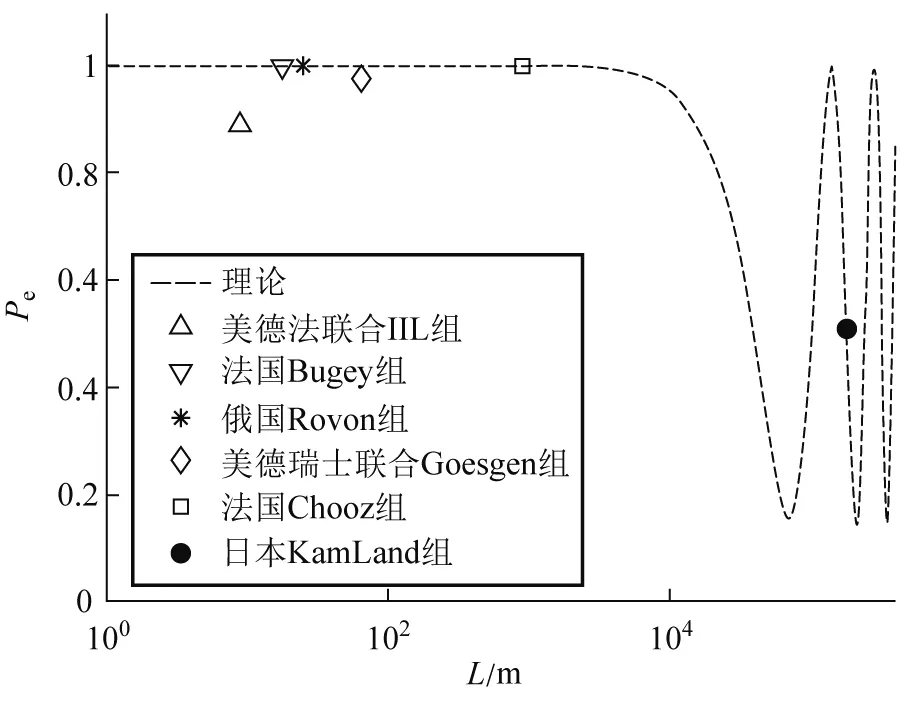
图1 反应堆中微子振荡的实验结果和理论分析

4 三代中微子情况的表象变换理论

4.1 中微子味表象和质量表象之间的表象变换

在第3节中，我们给出了中微子的两种表象：味表象和质量表象.进一步，利用两种表象之间的表象变换，分析了中微子状态随时间的演化行为：中微子振荡现象.理论分析和实验观测是完全一致的.当然，在第3节中，我们只讨论了两代中微子的情况，更完整的讨论应该包括3代中微子的情况.因此，我们将中微子的表象变换理论从2代中微子推广到3代中微子.

在味表象中，中微子的3种基矢态，即电子中微子、μ子中微子和τ子中微子分别标记为|ve〉、|vμ〉和|vτ〉.中微子的一般状态可以表示为这3种基矢态的叠加：

(30)

这一组数a1、a2和a3就构成了量子态在味表象中的表示.

在质量表象中，我们将3种质量本征态分别标记为|φ1〉、|φ2〉和|φ3〉，它们的质量为m1、m2和m3.在质量表象中，中微子的一般状态可以表示为这些质量本征态的叠加：

(31)

这一组数b1、b2和b3就构成了量子态在质量表象中的表示.

注意到，同一个态有

|Ψ〉=a1|ve〉+a2|vμ〉+a3|vτ〉=

b1|φ1〉+b2|φ2〉+b3|φ3〉

(32)

对于上式，左乘〈ve|、vμ|或者〈vτ|，我们可以得到如下关系式：

a1=〈ve|φ1〉b1+〈ve|v2〉b2+〈ve|φ3〉b3

(33)

a2=〈vμ|φ1〉b1+〈vμ|φ2〉b2+〈vμ|φ3〉b3

(34)

a3=〈vτ|φ1〉b1+〈vτ|φ2〉b2+〈vτ|φ3〉b3

(35)

很显然，上述关系式可以表示为矩阵的形式：

(36)

这个表象变换矩阵S显示同一个量子态在两个表象中的表示系数是联系在一起的.其中矩阵元素Sij是味表象的基矢|vi〉和质量表象的基矢|φj〉之间的标积Sij=〈vi|φj〉.这里的矩阵元素具有很明显的物理含义，即电子中微子态、μ子中微子态或τ子中微子态是由3种质量本征态混合而成的：

|ve〉=S11|φ1〉+S12|φ2〉+S13|φ3〉

(37)

|vμ〉=S21|φ1〉+S22|φ2〉+S23|φ3〉

(38)

|vτ〉=S31|φ1〉+S32|φ2〉+S33|φ3〉

(39)

如果用表象变换矩阵S，可以写成

|vi〉=∑jSij|φj〉

(40)

4.2 中微子振荡现象的理论分析和实验对照

这里，我们利用中微子的表象变换，来分析3代中微子状态的含时演化行为.设在初始时刻，产生了一个某种味i的中微子，在味表象下，该中微子的状态表示为

|Ψ(0)〉=|vi〉

(41)

这里i=e,μ,τ分别标记3种味本征态：电子中微子、μ子中微子和τ子中微子.利用表象变换式(40)，我们可以得到在质量表象下的式子：

|Ψ(0)〉=∑jSij|φj〉

(42)

这里j=1,2,3分别标记3种质量本征态.

进一步，我们可以得到t时刻的中微子状态为

|Ψ(t)〉=∑jSije-iEjt/ћ|φj〉

(43)

在t时刻探测中微子，会发现其不再是某种味i的状态|vi〉，而是转换为另一种味β的状态|vβ〉.这一转换过程的概率为

(44)

下面，我们利用上述公式，对于实验中关心的

几种典型情况进行分析.

第1种情况，我们讨论电子中微子和μ子中微子之间的转换.利用式(44)，可以计算初始时刻为电子中微子，末了转换为μ子中微子的概率为

(45)

第2种情况，我们讨论μ子中微子和τ子中微子之间的转换.利用式(44)，可以计算初始时刻为μ子中微子，末了转换为τ子中微子的概率为

(46)

5 教学效果分析

我们利用中微子振荡作为教学案例，来讲述表象变换理论.对于这种方式的教学效果，我们进行了问卷调查，让学生以一段话来评价这种教学方式.从调查结果来看，学生普遍给予了积极评价，主要可以归纳为如下2点：

1) 以中微子的味表象和质量表象作为具体例子，在讨论过程中，没有抽象的数学计算，而是把表象变换公式的物理含义揭示出来：表象变换矩阵元表示不同质量本征态的混合.这样的教学方式可以让学生们直观理解和掌握表象变换公式.

2) 以中微子振荡这一前沿成果作为教学例子，可以让学生了解当前的科研热点，让他们可以用所学的基本知识来理解前沿成果，而且是获得诺贝尔物理学奖的重要成果，这使得他们产生了强烈的兴趣和热情，学习的积极性得到较大提高.

6 结论

中微子振荡作为粒子物理学前沿，其基本思想可以用量子力学的表象变换理论很好的理解：在实验中产生和探测到的中微子味本征态|ve〉、|vμ〉和|vτ〉并不是质量本征态，而是质量为m1、m2和m3的3种质量本征态的线性组合.因此在飞行过程中，不同味本征态将会发生相互转换.

在教学中，我们利用中微子振荡作为具体案例，它很自然的包含了表象变换理论的几个基本概念：两个表象——味表象和质量表象，不同表象的变换矩阵——不同中微子态的混合.理论公式的计算比较简单，而且具有清晰的物理含义，能够很好地解释实验现象.

量子力学课程中融入前沿的研究成果，一方面可以培养学生利用抽象的理论公式解决具体物理问题的能力，另一方面这些具有前沿性和挑战性的内容，也极大鼓舞了学生对未知领域和前沿课题的探索兴趣.在本文中以中微子振荡作为典型案例，我们希望在今后的教学研究中，不断与时俱进，探索更多的前沿案例来丰富和促进量子力学的教学.