基于AHP-FEA权重分配方法的码垛机器人腰部转台多目标结构优化
贺 莹 王 丹 高 涵 马 超 陈 晔
(天津仁爱学院机械工程系,天津 301636)
高速重载码垛机器人已被广泛应用于现代化食品生产物流作业中。腰部转台是码垛机器人用于带动腰部支架以及其上机械臂实现腰部回转运动的基础零件,往复运动频繁,受载大且复杂。因此在腰部转台的设计过程中,其强度、刚度和振动稳定性是需要保证的重要指标,同时应使其质量尽可能小,以提高机器人系统的动态特性,降低能耗。
目前,有关机器人结构优化方面的研究较多,但大多针对机械臂[1-4],而针对腰部转台这类基础零件的研究却相对较少。鉴于高速重载码垛机器人的作业特点,针对其基础性零件的结构优化设计需要在动力学层面开展研究,通过振动激励测试试验测得工作过程中的激励力频率,并与基础性零件的固有频率比较,判定动力学性能优化指标。同时,结合静力学分析开展多目标结构优化设计研究[5-6]。
此外,通过多目标优化求解可以得到满足优化目标的Pareto解集,该解集是一个包含多组优化设计方案的集合,需要通过构建各项优化指标的权重系数,从Pareto解集中选择出最满意的优化方案。权重系数通常由设计者根据经验定性地确定,比如平均分配法[7-8]或经验赋权法[9-10]等,具有较强的主观性。研究拟引入层次分析法(Analytic Hierarch Process,AHP)[11-12],获得各项性能指标的权重,并提出一种基于有限元分析的层次分析法(AHP-FEA),即依据有限元分析结果考察各个优化目标的重要性,以提高比较矩阵的客观性,旨在形成一种更加科学,优化效果更优的权重系数分配方法。
1 研究方案
MD1200-YJ码垛机器人的三维模型如图1所示,该机器人的性能参数和机构参照文献[5-6]。腰部转台的下部与腰关节RV减速器输出端连接,其上部与腰部支架连接。伺服电机通过腰关节RV减速器驱动腰部转台转动,进而带动腰部支架以及其上安装的机械臂实现腰关节的回转运动。
研究方案:建立腰部转台的有限元模型,对腰部转台进行静力学分析、模态分析以及振动激励测试,确定优化目标、设计变量以及约束条件,利用试验设计和响应面法建立优化目标函数的近似模型,利用AHP-FEA方法获得各项性能指标的权重系数,建立综合评价指标;利用NSGA-Ⅱ算法进行优化求解;通过与常用的平均分配法和经验法两种赋权方法获得的优化结果进行对比,验证AHP-FEA方法的优越性,并完成腰部转台的优化设计。
2 多目标结构优化设计
2.1 有限元模型建立
腰部转台模型如图2所示,质量83.458 kg。
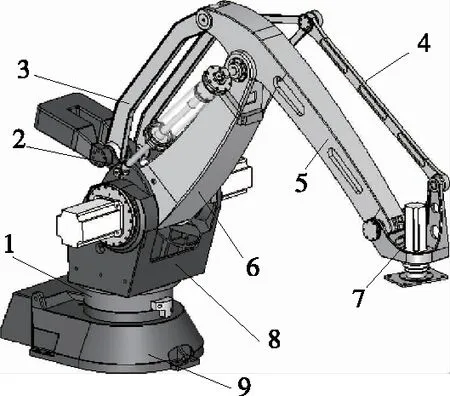
1. 腰部转台 2. 小臂驱动臂 3. 小臂驱动连杆 4. 水平保持连杆 5. 小臂 6. 大臂 7. 末端执行器 8. 腰部支架 9. 机座图1 MD1200-YJ码垛机器人模型Figure 1 MD1200-YJ palletizing robot model

图2 三维模型Figure 2 3D model
(1) 材料属性:QT500-7,弹性模量1.62×1011Pa;泊松比0.3;抗剪模量6.27×1010Pa;密度7×103kg/m3;屈服强度3.2×108Pa[13]。
(2) 网格划分:四面体网格,最大单元45.697 mm;最小单元9.139 mm;节点总数44 542;单元总数26 160。有限元模型,如图3所示。

图3 有限元模型Figure 3 Finite element model
2.2 腰部转台静力学分析
2.2.1 施加位移约束 根据装配关系,在腰部转台的底面施加固定约束。


图4 运动部件受力分析Figure 4 Force analysis of moving parts
(1)
∑Fz′=0FN=G1+G2,
(2)
(3)
(4)

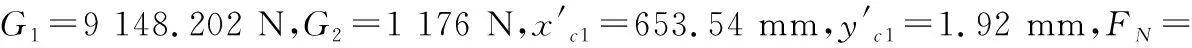
2.2.3 静力学分析求解 经静力学分析求解,腰部转台的等效最大应力为12.972 MPa,远小于材料的许用应力;总变形量最大值约0.017 mm,如图5和图6所示,因此,腰部转台具备轻量化设计的潜力。

图5 等效应力Figure 5 Equivalent stress

图6 总变形量Figure 6 Total deformation
2.3 振动稳定性分析
振动稳定性的设计准则是使腰部转台的固有频率和外载荷激励频率互相远离,需要进行动态分析,包括模态分析和振动激励测试。模态分析可以获得零件的固有频率和振型,振动激励测试可以获得机器人运动过程中,零件受到的外载荷激励频率。
2.3.1 模态分析 对于一个n自由度无阻尼系统的自由振动方程一般形式为
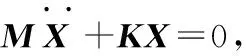
(5)
式中:

在系统自由振动中,假设所有的质量均做简谐运动,则方程解的形式为
Xi=A(i)sin(ωnit+φi),i=1,2,3,…,n,
(6)
式中:
Xi、A(i)、ωni、φi——第i个振型的n个位移列阵、幅值向量、固有频率(单位:rad/s)和相位角(单位:rad)。
将式(6)代入方程式(5),得:
(7)
令
(8)
式(8)称为特征矩阵。
由式(7)可知,要使A有不全为零的解,则必须有
(9)
由式(9)可以求得n个固有频率。
将各个固有频率代入式(7),可以求得相应的主振型矢量A(i)。
n自由度振动系统,具有n个固有频率和与之对应的n阶主振型。各主振型之间存在着关于质量矩阵和刚度矩阵的正交性。
对式(7)右乘转置A(i)T可以得到
(10)
由于M是正定的,K是正定或半正定的,由式(10)可以得到
(11)
由此可知,在保证结构刚度不降低的情况下,减小质量,可以增大固有频率,提高系统的动态性能。
对腰部转台进行模态分析,此处只给出前两阶模态振型,如图7所示。一阶固有频率824.97 Hz,一阶振型为绕x偏z45°和绕z偏-x45°方向对角两两往复扭动;二阶固有频率854.99 Hz,二阶振型为绕x和z轴对角两两往复扭动。

图7 前两阶模态振型Figure 7 The first two modes
2.3.2 振动激励测试 采集机器人工作过程中腰部转台受到的激励信号,结合模态分析结果考察其振动稳定性。主要试验设备见表1。

表1 试验设备Table 1 Experimental equipment
连接螺钉是振动在零件之间传递的“桥梁”,所以将加速度传感器布置于腰部转台与其上腰部支架连接螺钉处测量激励信号。仪器设置:采样时间30 s,带宽1 024 Hz,分辨率0.125 Hz。测取测试点-x、+y、-z3个方向的加速度频谱,此处只给出#1和#2两个测试点的加速度频谱,结果见图8。
由图8可知,#1和#2测试点3个方向的加速度频谱变化趋势相似,但峰值存在差异,这与两点位处结构的连接刚度差异有关;测试点-x和-z方向的加速度峰值对应的频率约为388 Hz,+y方向的振动加速度峰值对应的频率为1 557 Hz,均与腰部转台的第一阶固有频率值(824.97 Hz)距离较远,表明腰部转台出现共振的几率较低,具有较好的振动稳定性。考虑到码垛机器人的运动平稳性及定位精度要求较高,提高第一阶固有频率有利于保证结构的整体刚度,因此在优化过程中以第一阶固有频率最大作为优化目标之一。

图8 加速度频谱图Figure 8 Acceleration spectrum
2.4 优化建模
2.4.1 设计变量 选取腰部转台的4个相互独立且非装配尺寸的结构参数为设计变量X=(x1,x2,x3,x4),如图9所示,对应的名称、初始值以及取值范围见表2。
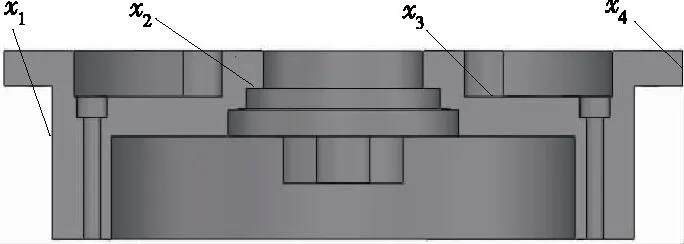
图9 设计变量指示图Figure 9 Design variables indicator diagram
2.4.2 目标函数 由腰部转台的设计准则、静力学分析以及动力学分析确定,以质量最小、最大位移最小、第一阶固有频率最大、最大应力最小为优化目标,其目标函数:
(12)
采用Box-Behnken试验设计方法,结合表2设计变量数据,建立25组试验设计方案,根据各组设计方案,更改模型结构参数,并逐一通过质量测算、静力学分析和模态分析分别完成质量m、最大应力σmax、最大位移δmax、第一阶固有频率f1的计算,得到试验设计矩阵及结果见表3。利用RSM方法获得4个优化目标函数的近似模型:m(X),δmax(X),f1(X),σmax(X)。
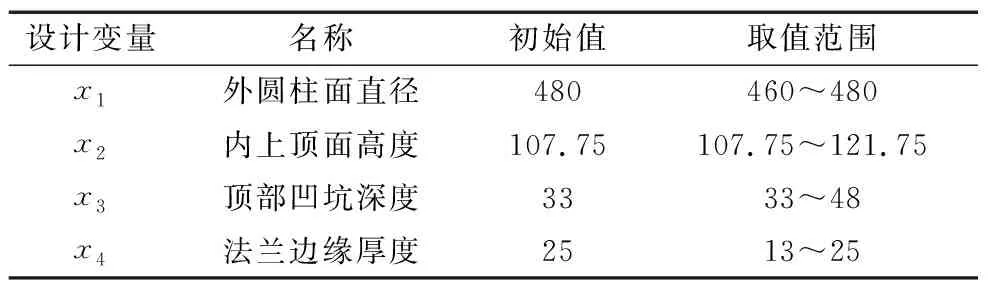
表2 设计变量表Table 2 Design variables tablemm
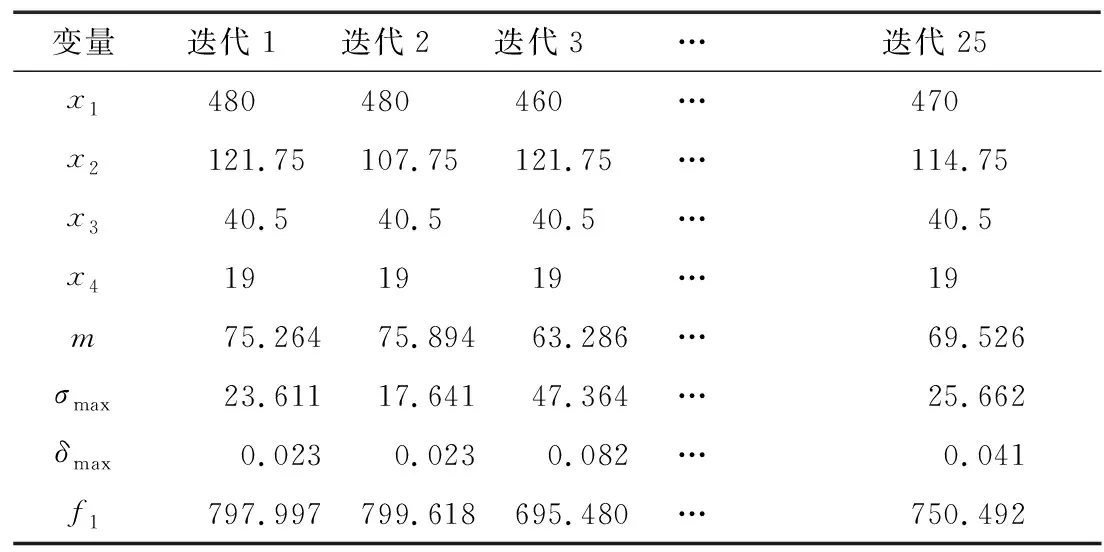
表3 试验设计矩阵Table 3 Experiment design matrix
2.4.3 约束条件 以各设计变量的边界条件作为约束条件。
(1) 变量x1和x4为腰部转台的厚度尺寸,其尺寸越小,质量越轻,因此以各尺寸的初值为最大值,以剩余材料厚度不小于球墨铸铁最小壁厚[13]为原则选取最小值。
(2) 变量x2和x3为腰部转台的深度尺寸,其尺寸越大,质量越轻,因此以各尺寸的初始值为最小值,以剩余材料厚度不小于球墨铸铁最小壁厚为原则选取最大值。
2.4.4 权重系数的确定 提出一种基于有限元分析结果的层次分析法确定权重系数。层次分析法的原理参照文献[11-12]。
(1) 建立递阶层次结构模型。将优化问题分成目标层、准则层和方案层3个层次,如图10所示。

图10 递阶层次结构模型Figure 10 Hierarchical substructure model
(2) 构造比较矩阵。质量、位移、第一阶固有频率、应力分别用B1、B2、B3、B4表示。依据有限元分析结果,考察各性能指标的重要性。从有限元静力和动力学分析结果来看,最大应力、最大位移均远小于许用值,第一阶固有频率与激励频率相距较远,说明腰部转台轻量化的潜力较大,因此将减轻质量作为主要目标,其重要性排第一。对于第一阶固有频率、位移和应力的重要性评价:最大位移较小,但是机器人的臂杆尺度长,对腰部转台的变形量具有放大作用,容易增大机器人末端的位置误差,故最大变形量应越小越好,因此其重要性排第二;第一阶固有频率比较高,振动稳定性比较好,但是提高第一阶固有频率,有利于提高结构的整体刚度,因此其重要性排第三;最大等效应力值远小于QT500-7的许用应力,安全系数较大,其重要性排第四。因此,准则层各因素两两比较结果见表4,并得到比较矩阵式(13)。

表4 各因素的影响程度比较Table 4 Compare the influence degree of each factor

(13)
矩阵A的最大特征值λmax=4.019 2;相应的特征向量为ω*=(0.914 2,0.191 2,0.339 2,0.112 4)T。
(3) 一致性检验:一致性指标CI=0.006 4<0.1;随机一致性指标RI=0.9;一致性比率CR=0.007<0.1。
据此,可以判定比较矩阵A通过一致性检验,将特征向量ω*归一化处理得到Fm(X)、Fδ(X)、Ff1(X)和Fσ(X)4个优化目标的权重向量:
ωA=(0.587 2,0.217 9,0.122 8,0.072 2)T。
同时,选取两种常见的权重系数分配方案:第一种为基于平均分配法确定权重系数,4个优化目标同等重要,即:
ωT=(0.25,0.25,0.25,0.25)T。
第二种为基于经验法确定权重系数,4个优化目标重要性依次降低,即:
ωJ=(0.4,0.3,0.2,0.1)T。
2.4.5 综合目标函数的建立 根据4个分目标函数以及3种不同的权重系数向量,构建综合目标函数:
(14)
由于优化设计的目标是使综合目标函数值最小化,而其中第一阶固有频率的目标是使其最大化,因此其前面加负号。式(14)可作为3种赋权方法优劣的评价指标,综合目标函数值越小,说明所获得的优化设计方案的综合效果越优。
2.5 多目标优化求解
采用性能优越的NSGA-Ⅱ算法[14]分别对3种权重系数分配方案下构建的综合目标进行优化求解。参数配置:种群规模为40;代数为200;交叉率为0.9;交叉分布指数为10;变异分布指数为20。
2.6 结果与分析
通过计算求解得到优化后结构参数及相应的结构性能参数,如表5所示。由表5可知,3种权重系数下,腰部转台的质量均有不同程度的减小,其中采用AHP-FEA权重系数优化的质量最小,最大位移和最大应力值均有不同程度的增大,但均在许用范围内,第一阶固有频率变化不大。将3种方法获得的优化后的最小(大)化的结构性能参数值[Fm(X)、Fδ(X)、Ff1(X)、Fσ(X)]代入式(14),分别计算综合目标函数值。结果表明,采用AHP-FEA权重系数下的优化综合目标函数值最小,说明该方法综合优化效果更优。

表5 不同权重系数下的优化结果Table 5 Optimization results under different weight coefficients
考虑结构工艺性,对AHP-FEA权重系数下的优化结果进行圆整,根据最终结构参数重构三维模型,得到优化后的目标性能参数,结果见表6和图11~图13,经多目标结构优化,外圆柱面直径(x1)无变化;内上顶面高度(x2)和顶部凹坑深度(x3)均有增大,相对应的结构厚度分别减小了6.25,4.00 mm;法兰边缘厚度(x4)减小了10 mm。腰部转台质量减小了9.6%,最大总位移增大了约0.009 mm,最大等效应力值增大了5.759 MPa,但仍在允许范围内,其结构强度和刚度仍充分满足要求;第一阶固有频率增加了1.31 Hz,使之更加远离腰部转台受到的外载荷激励频率,提高了振动稳定性,也充分验证了“在保证结构刚度不降低的情况下,减小质量,可以增大固有频率”的论断。通过优化研究,腰部转台的整体结构性能得到提升,提高了码垛机器人的动态性能,达到结构优化的设计目的,验证了优化方法的有效性。

表6 优化结果及性能参数Table 6 Optimization results and performance parameters

图11 优化后模型的等效应力Figure11 Equivalent srtess of optimized model

图12 优化后模型的总位移Figure 12 Total deformation of optimized model

图13 优化后模型的一阶振型Figure 13 The first modal shape of optimized model
3 结论
针对MD-1200YJ码垛机器人腰部转台的多目标结构优化问题进行了研究,提出了一种基于有限元分析的改进层次分析方法(AHP-FEA)来确定各分优化目标权重系数,并与常用的平均分配法和经验赋权法进行对比,证明了AHP-FEA方法的优越性。通过优化设计,腰部转台结构性能得到进一步提升。从优化后的最大应力和位移值可以看出,腰部转台仍具有较大的轻量化设计的潜力,后续可以考虑基于形状优化、拓扑优化等方法,进一步探讨其结构优化问题。

