密度峰值隶属度优化的半监督Self-Training 算法
刘学文,王继奎+,杨正国,李 冰,聂飞平
1.兰州财经大学 信息工程学院,兰州 730020
2.西北工业大学 光学影像分析与学习中心,西安 710072
目前,数据规模大幅增长,但有标签数据的获取成本仍然较高,大部分数据只含有少量标签。不同于监督学习和无监督学习,半监督学习允许利用数据集中的大量无标签数据和少量有标签数据。Self-Training 算法是半监督学习算法家族中的一员,其实现方式开放灵活,可以适应多样的半监督学习任务。
Self-Training 算法在迭代过程中,从无标签样本中选取高置信度样本并由基分类器赋予其标签,将这些样本和标签添加进训练集,迭代训练输出优化后的分类器。然而,如果带有错误标签的样本被添加进训练集,将导致半监督分类性能降低。为降低此类风险,研究者们提出了各种选取高置信度样本的方法。
文献[6]提出了编辑自训练算法(self-training with editing,SETRED),采用割边权重统计(cut edge weight statistic,CEWS)方法,利用左侧检验将含有较多割边的样本从训练集中移除,SETRED 算法的计算开销较大,而且当样本在相关邻近图(relative neighborhood graph,RNG)上的近邻数量较少或者割边权重不平衡时,假设检验的效果不佳。聚类算法是一种有效的发现样本潜在信息的方式,它可以从大量无标签样本中提取有价值的信息来辅助高置信度样本的选取。文献[11]基于聚类假设提出了基于半监督模糊C 均值聚类的自训练算法(using clustering analysis to improve semi-supervised classification,STSFCM),在Self-Training 迭代过程中嵌入半监督模糊C 均值(semi-supervised fuzzy C-means algorithm,SSFCM)聚类算法,将类簇隶属度大于设定阈值的样本作为高置信度样本。STSFCM 算法从训练集中移除类簇归属确定性低的样本是一种有效的思路,然而该算法对非球形数据聚类的效果不理想,且易受初始点选择的影响,因此,有研究者尝试在Self-Training 算法中嵌入DPC(density peaks clustering)算法。DPC 是一种简单、快速、有效的聚类算法,它可将任意维度数据映射成二维,利用密度峰值在二维空间内建构数据之间的层次关系,而且对于非球形数据也具有较好的适应性。近年来,DPC 算法的研究热度不减,文献[16-20]从密度峰值计算、聚类中心选取和数据点分配等方面提出了改进方法,文献[21]利用密度峰值对模糊C 均值(fuzzy C-means,FCM)聚类算法中初始聚类中心、类簇数目选择等过程进行了优化。文献[22]提出基于数据密度峰值的自训练半监督分类算法(self-training semi-supervised classification based on density peaks of data,STDP),在DPC 算法发现的层次空间结构中,先标记有标签样本的无标签“前驱”,再标记无标签“后继”。文献[23]通过局部密度阈值将样本划分为核心点和边界点,并依次赋予标签、添加进训练集。文献[24]将STDP 算法与SETRED 算法结合,用CEWS 方法检验选取的高置信度样本,进一步提升了训练集的质量。
DPC 算法的一个重要创新就是提出“峰值”这一概念,峰值的本质是距离,但峰值带有密度指示方向——低密度点指向距离其最近的高密度点。密度相对更高的样本点通常是局部中心点,在Self-Training 迭代过程中,中心点的重要程度比边缘点更高。因此,本文受DPC 思想的启发,定义“簇峰值”和“密度峰值隶属度”,提出密度峰值隶属度优化的Self-Training 算法(semi-supervised self-training algorithm for density peak membership optimization,STDPM)。STDPM 算法的主要工作如下:
(1)利用DPC 算法密度峰值计算过程中发现的数据潜在空间结构,定义原型树和近亲结点集。
(2)利用近亲结点集中的无标签样本与不同类别有标签样本之间的局部密度与距离关系,定义簇峰值和密度峰值隶属度。
(3)利用密度峰值隶属度,选取大于设定阈值的样本作为高置信度样本,添加进训练集,迭代优化分类器。在8 个基准数据集上的实验结果验证了STDPM 算法的有效性。
1 相关工作
1.1 符号说明
将本文中常用的符号和相关说明列在表1 中。

表1 STDPM 中的符号Table 1 Notations in STDPM
1.2 Self-Training 算法
Self-Training 算法是一种简单高效的利用无标签数据的半监督学习框架,通过在迭代过程中生成“伪标签”替代真实标签,达到优化模型的目标。标准的Self-Training 算法通常利用基分类器生成“伪标签”,最后输出优化后的分类器,主要过程如下:
(1)在有标签样本集中训练分类器;
(2)从无标签样本集中选取一部分高置信度样本集,并由赋予“伪标签”;
(3)将添加进中,并从中移除;
(4)返回(1),直至稳定或中没有样本时停止,输出。
在Self-Training 算法中,涉及一个关键的问题,即如何选取高置信度样本,本文主要针对这个问题进行研究。如果高置信度样本选取不当,“伪标签”变成“错误标签”会污染训练集,进而使得分类性能下降。接下来简要介绍两种具有代表性的、采用不同高置信度样本选取方法的Self-Training 算法。
1.3 STSFCM 算法
STSFCM算法利用半监督聚类SSFCM隶属度选取高置信度样本,最小化以下目标函数:
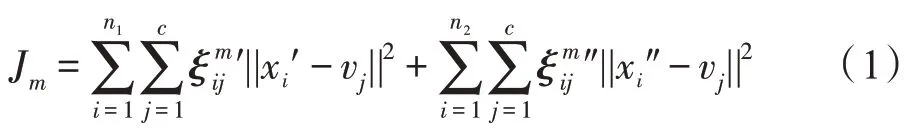
其中,有标签样本′∈,无标签样本″∈,为类簇数,v为第个类簇中心,′为有标签样本的隶属度矩阵,″为无标签样本的隶属度矩阵。
用拉格朗日乘子法,获得无标签样本x″的隶属度:

SSFCM 基于FCM 算法,利用有标签样本的先验知识改善聚类效果,STSFCM 则通过设定一个阈值,利用SSFCM 的隶属度改善分类效果,将ξ″≥的无标签样本作为高置信度样本集′,然后在′中训练支持向量机(support vector machine,SVM),选取SVM 分类器输出的概率值f≥的样本作为更高置信度的样本集″。
1.4 STDPCEW 算法
结合密度峰值和切边权值的自训练算法(selftraining algorithm combining density peak and cut edge weight,STDPCEW)在STDP算法的基础上,结合SETRED算法,采用假设检验的方式选取高置信度样本。
首先,利用DPC 发现样本的潜在空间结构,找到有标签样本的“前驱”样本集和“后继”样本集。
其次,在⋃中构造相关邻近图,图中顶点满足条件d≤max(d,d),∀≠,,计算内样本点的割边权重和J:

其中,W为割边权重,I的值为0 或1,当x的标签Y等于x的标签Y时I=0,否则I=1。J在零假设下服从正态分布(,),和的计算如下:
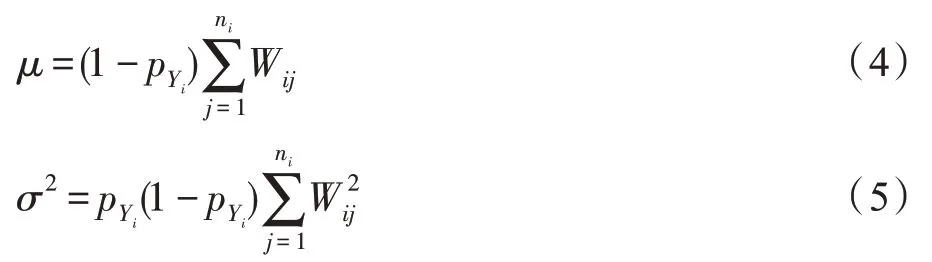
其中,p表示样本标签为Y的概率。
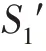
2 密度峰值隶属度优化的Self-Training 算法
2.1 原型树
根据文献[14]中DPC 算法的定义,给定样本x的局部密度(截断核)计算如下:
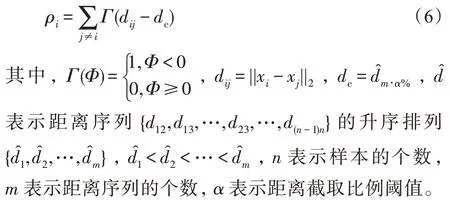
样本x的局部密度(高斯核)计算如下:

样本x的峰值计算如下:
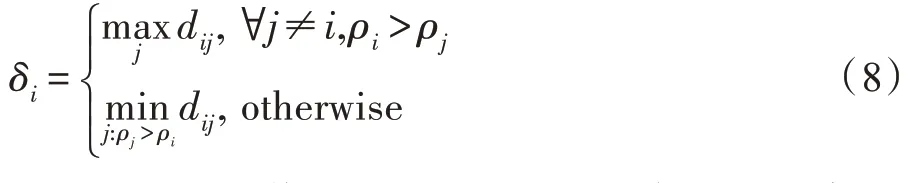
由公式知,峰值是低密度点与距其最近的高密度点之间的距离,其融合了密度与距离信息,由峰值的计算引出原型的定义。
样本x的原型P定义为:

由公式知,低密度点的原型即为离其最近的高密度点。对于密度最高的点,由于没有比它密度更高的点,其原型为自身,即P=x,∀≠,ρ>ρ。
由样本与其原型之间的联系可以递归构造出原型树,主要过程如下:
(1)确定原型树的根结点:密度最高的点作为根结点,根结点x须满足条件∀≠,ρ≥ρ。
(2)确定除根结点之外的父结点:x的原型P为其父结点,即x的父结点满足条件x=P。
随机生成3 类别的高斯分布样本,每个类别包含5 个样本,表2 为样本的密度峰值和原型等信息。
由表2 中的样本绘制图1 中的原型树。表2 中数值精确到小数点后3 位,为便于比较,每个样本的和值已经归一化。根据文献[14]中的定义,类簇中心为和值均较大的样本点,因此,和的乘积值较大的点可作为类簇中心。
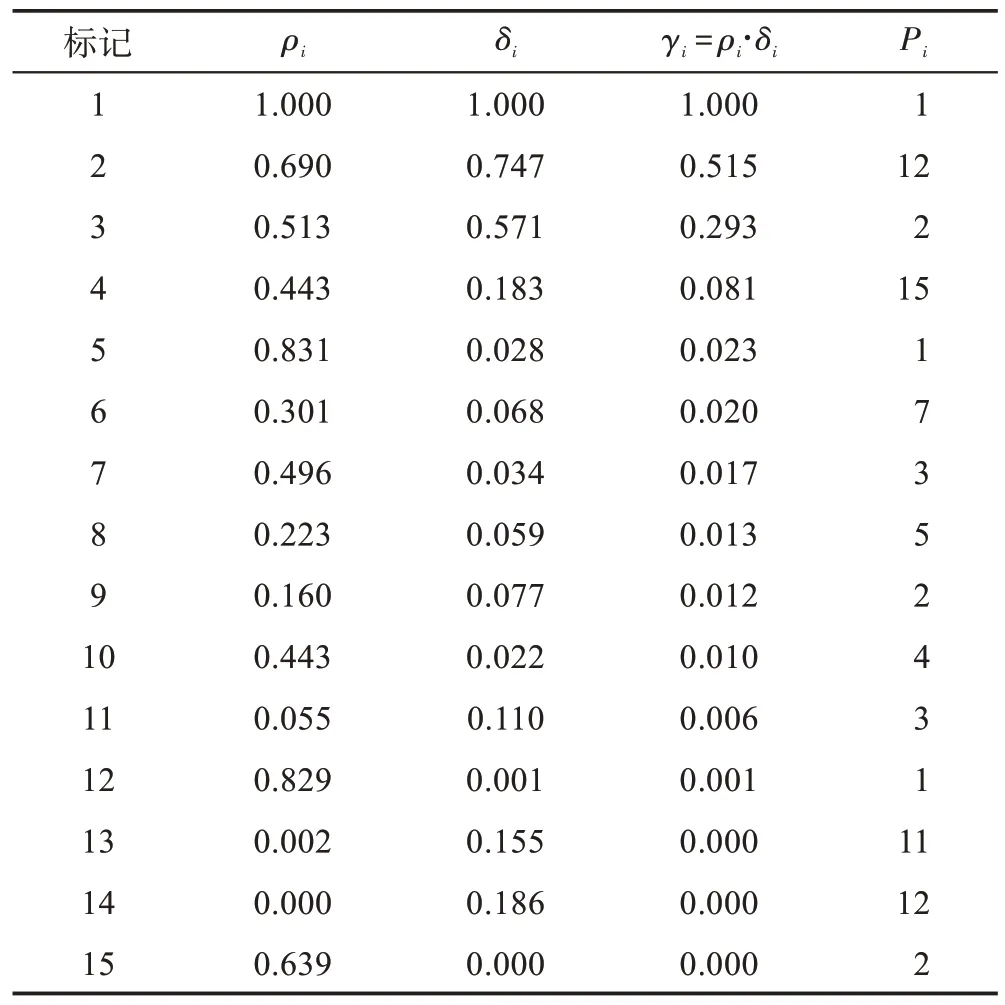
表2 样本信息Table 2 Samples information

图1 样本分布和原型树示意图Fig.1 Samples distribution and illustration of prototype tree
图1(a)中圆、矩形和六边形表示不同类别的样本,箭头指示样本点的原型,如样本13 的原型为样本11。虚线椭圆内区域为类簇中心区域,由表2 知样本1、样本2 和样本3 的值较大,因此它们分别为各自所在类簇的中心点。
图1(b)为图1(a)中样本的原型树结构的树状示意图,由表2 知样本1 的值最大,因此其作为根结点,样本5 和样本12 的原型为样本1,样本8 的原型为样本5,样本2 的原型为样本12,根据表2 中每个样本的原型,可以递归构造原型树。
2.2 近亲结点集
在原型树中,任意结点至少存在父结点、子结点或兄弟结点中的一种结点。不同于一般的近邻关系,由图1 可知,原型树上结点的“近邻”关系是基于峰值的,本文将这种特殊的“近邻”关系定义为“近亲”关系,原型树中的所有近亲构成其近亲结点集,给出如下定义。
样本x的近亲结点集R定义为:
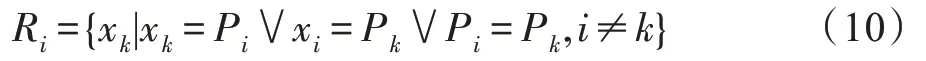
由公式知,x的近亲结点集即为其父结点、子结点和兄弟结点构成的一个集合。如图1(b)所示,样本3 的父结点为样本2,兄弟结点为样本9 和15,子结点为样本7 和11,则样本3 的近亲结点集={,,,,}。
在原型树上搜索每一个有标签样本的近亲,获得近亲结点集=⋃⋃…⋃R,其中为有标签样本的个数。从中移除所有的有标签样本,得到有标签样本的无标签近亲结点集R=-。
2.3 密度峰值隶属度
在硬聚类算法中,每个样本隶属于某个类簇是确切的,要么属于某个类簇要么不属于某个类簇,隶属度取值为0 或1。而在软聚类算法中,样本隶属于某类簇的隶属度是模糊的,其取值范围为[0,1]。
在对类别的数据进行聚类的过程中,如果样本x的隶属度U≫U,≠,∀∈[1,],则x具有更确切的归属,x被分类器误分的可能性也会更小。反之,如果样本的隶属度之间相差较小,则其被误分的可能性更大。因此,STDPM 通过设定一个阈值,将密度峰值隶属度大于阈值的样本作为高置信度样本,密度峰值隶属度由簇峰值权重归一化后得到,先定义簇峰值:
给定样本x是无标签近亲结点集R内的点,样本x是有标签样本集中的点。样本x的簇峰值ζ定义为:
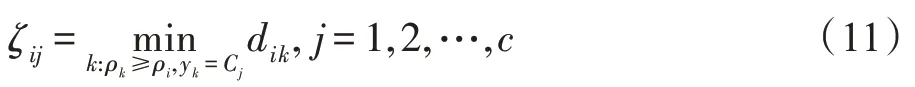
其中,表示类簇的个数;y表示样本x的标签;C表示第个类的标签;d表示样本x与样本x的欧式距离。
图2 为簇峰值的计算示意图。图2 中不同形状表示不同的类簇C,有颜色填充形状表示有标签样本,无颜色填充表示无标签样本。如图2 所示,在簇、和中,距样本11 最近且密度更大的有标签样本分别为样本2、样本3 和样本12,则样本11 对应的簇峰值分别为=,=,=。

图2 簇峰值计算示意图Fig.2 Illustration of calculating clusters-peak
由簇峰值计算簇峰值权重,其中为中的最大值,给定样本x对应第类的簇峰值权重W计算如下:

由公式知,ζ越大,W就越小,样本x隶属于第类的概率就越小。将簇峰值权重按行归一化后得到密度峰值隶属度,给出如下定义:
给定样本x是无标签近亲结点集R内的点,样本x的密度峰值隶属度ξ定义为:

其中,为ζ中最大值,为ζ中最小值。
无标签样本的密度峰值隶属度,取决于在各类簇中密度比它更高且距离它最近的有标签样本,而不是仅取决于离它最近的或者密度比它高的样本。密度峰值隶属度充分地利用了样本的密度和峰值信息,兼顾了数据的全局与局部特性。
2.4 算法描述
密度峰值隶属度优化的Self-Training算法(STDPM)从无标签近亲结点集中,选取隶属度值较高的样本作为高置信度样本,将其添加到训练集,迭代训练分类器。STDPM 算法描述如算法1 所示。
STDPM 算法

2.5 算法分析与讨论
令表示输入样本的个数,表示维度,表示迭代次数。STDPM 算法计算密度峰值的时间复杂度为(),构造原型树的时间复杂度为(),计算簇峰值、簇峰值权重和密度峰值隶属度的时间复杂度为(),因此,STDPM 算法的整体时间复杂度为()。SETRED 和STDPCEW 算法的时间复杂度主要在于构造相关邻近图,其整体时间复杂度为()。STDP 算法的时间复杂度主要在于计算密度峰值,其整体时间复杂度为(),STSFCM 算法计算模糊隶属度的时间复杂度为(),训练SVM 分类器的复杂度为(),其整体时间复杂度为()。因此,由上述分析可得结论:STDPM 算法的时间复杂度低于SETRED、STSFCM 和STDPCEW 算法,但与STDP 算法一致。STDP、STDPCEW 和STDPM 算法的空间复杂度主要在于计算密度峰值,整体空间复杂度均为(),SETRED 的空间复杂度主要在于构造相关邻近图,其整体空间复杂度为(),STSFCM算法的空间复杂度主要在于计算模糊隶属度和SVM分类器的训练、预测,其整体空间复杂度为()。
STSFCM 算法在非球形数据上的分类效果不佳,STDPCEW 利用密度峰值发现数据结构,在球形数据上的分类效果较好,但是对于大数据集,其构造相关邻近图的时间复杂度高。STDPM 算法也利用密度峰值信息构造原型树,利用密度峰值隶属度选取高置信度样本,不仅适用于非球形数据,而且没有增加时间复杂度。
3 实验结果与分析
所有实验基于64 位的Windows 10 系统、Matlab 2019b,处理器为Intel Core i5,内存为8 GB。实验涉及的对比算法均参照原文实现,所使用的其他算法均来自Matlab 工具箱。
3.1 对比算法与数据集
选取4 个相关的Self-Training 算法与STDPM 算法进行对比,分别为SETRED、STDP、STDPCEW、STSFCM。
5 个算法均采用最近邻分类器(nearest neighbor,NN)作为基分类器,各个算法的参数设置如表3所示。因为STSFCM 采用了NN 作为基分类器,所以,其阈值参数只有一个。

表3 参数设置Table 3 Parameters setting
为验证STDPM 算法的有效性,在选取的8 个基准数据集上进行实验,数据集信息如表4 所示。其中Banknote、Breast、Hepatitis、Ionosphere、Palm、Segment和Zoo数据集均来源于公开的UCI数据库(http://archive.ics.uci.edu/ml/index.php),Yale(32×32)数据集来源于公开的耶鲁大学人脸数据库(http://cvc.cs.yale.edu/cvc/prjects/yalefaces/yalefaces.html)。
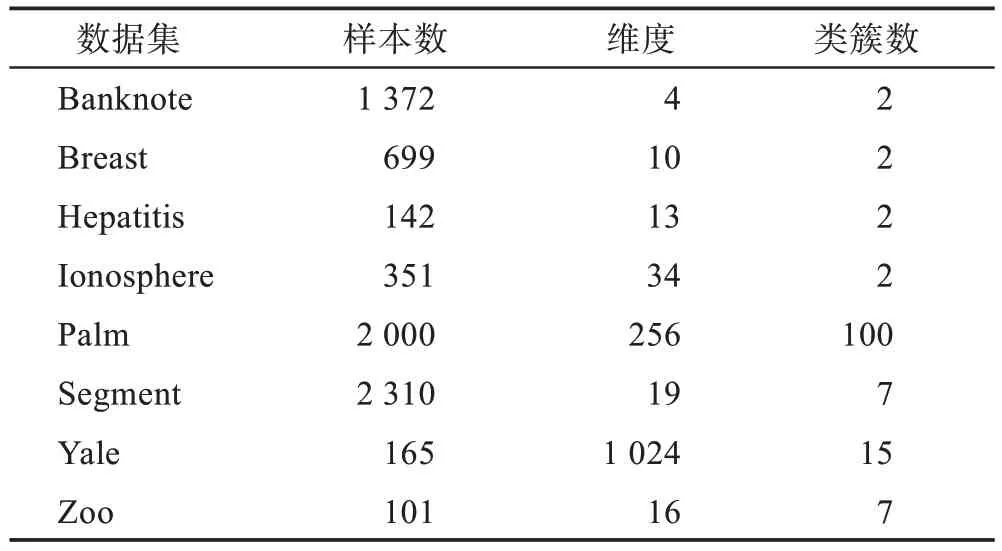
表4 数据集信息Table 4 Datasets information
表4 中,大部分数据集的维度较高,为便于实验对比,先将维度大于10 的数据集用PCA 降到10 维,小于10 维的数据集则保持不变。
3.2 分类性能分析
为验证STDPM 算法的有效性,表3 中5 个对比算法按照设定参数,在表4 的8 个基准数据集上进行实验。
5 个算法在每个数据集上运行30 次:随机抽取10%的数据作为有标签数据,其余90%作为无标签数据,将这两类数据作为算法的输入数据;将不做划分的原始数据集作为固定测试集,记录算法最终输出分类器的测试准确率(Accuracy)和F 分数(F-score)。
计算5 个算法在对应的数据集上的测试准确率和F 分数的均值(mean)与标准差(std),实验结果如表5 和表6 所示,每个数据集上的最高性能以加粗字体显示。
由表5 可知,STDPM 在Banknote、Breast、Hepatitis、Ionosphere 数据集上都获得了最高的分类性能,Accuracy 值分别高出第2 名0.18 个百分点、0.10 个百分点、2.10 个百分点和0.78 个百分点,F-score 值分别高出第2 名0.14 个百分点、0.09 个百分点、2.44 个百分点和0.62 个百分点。因为4 个数据集的数据分布较平衡,所以Accuracy 值和F-score值趋于一致。
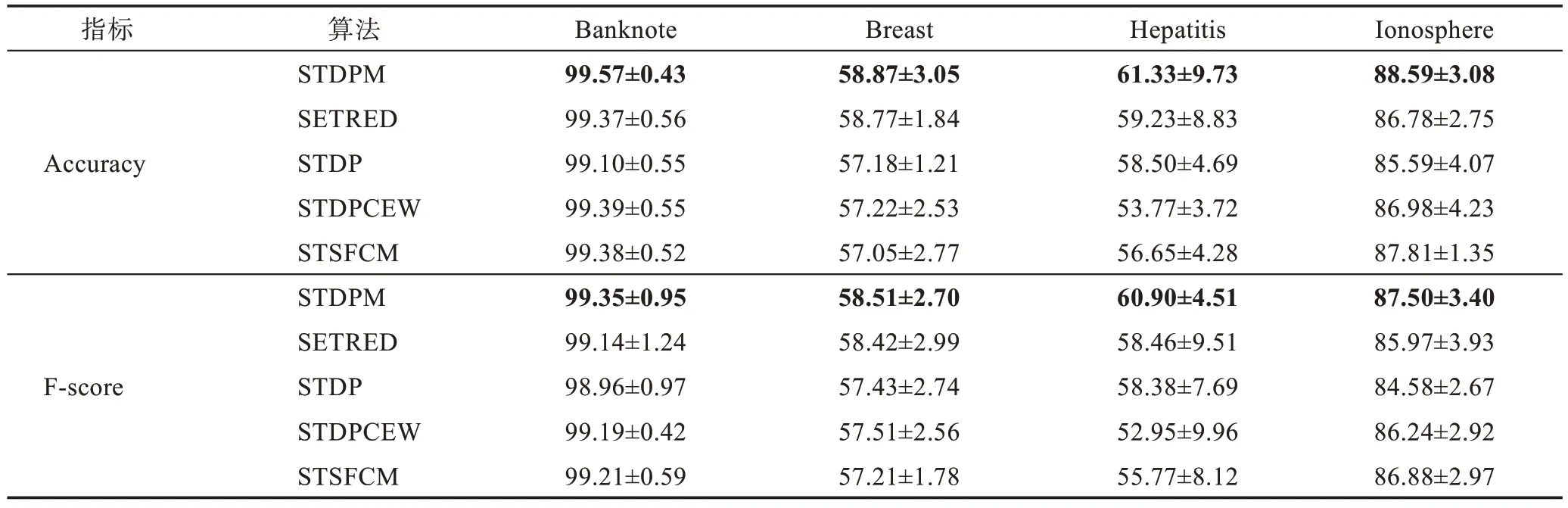
表5 在数据集Banknote、Breast、Hepatitis和Ionosphere上的性能(mean±std)Table 5 Performance on Banknote,Breast,Hepatitis and Ionosphere datasets(mean±std) 单位:%
由 表6 可知,STDPM 在Palm、Segment、Yale 和Zoo 数据集上都获得了最高的分类性能,Accuracy 值分别高出第2 名0.04 个百分点、0.10 个百分点、0.29个百分点和2.81 个百分点,F-score 值分别高出第2 名0.13 个百分点、0.11 个百分点、1.83 个百分点和5.33个百分点。
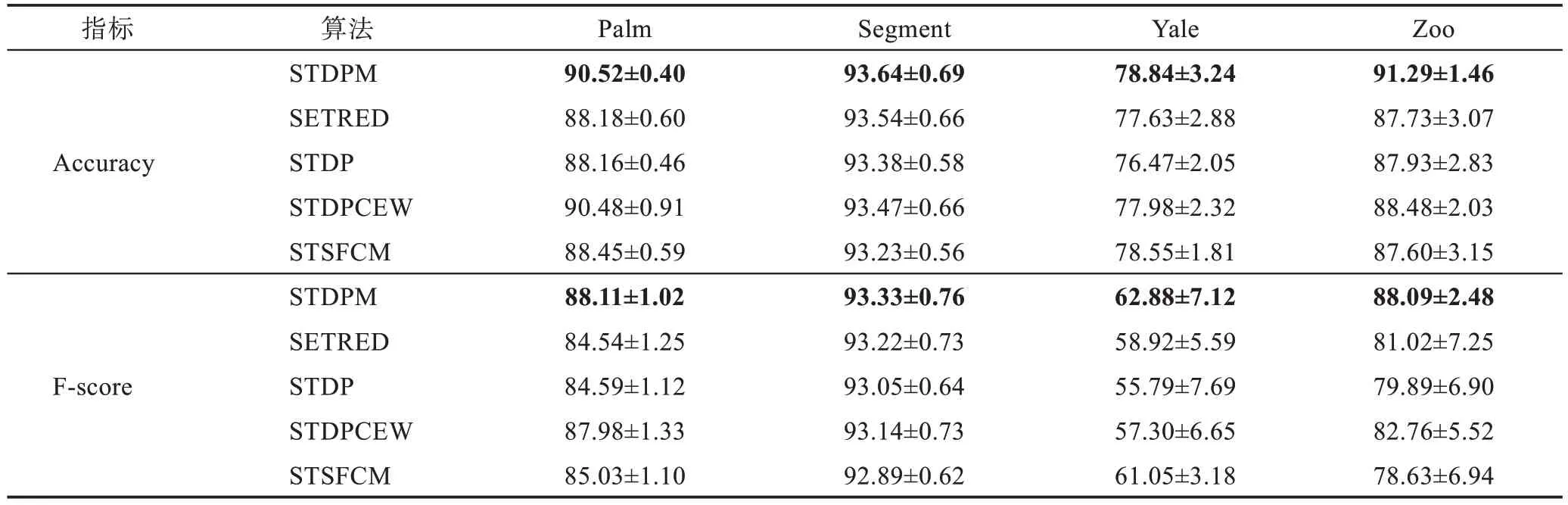
表6 在数据集Palm、Segment、Yale和Zoo 上的性能(mean±std)Table 6 Performance on Palm,Segment,Yale and Zoo datasets(mean±std) 单位:%
虽然Zoo数据集的数据分布不平衡,但是STDPM的分类性能却显著高于其他算法,这表明STDPM 能充分利用密度峰值发现样本的局部结构信息,提升分类性能。
3.3 有标签样本比例对性能的影响
有标签比例过低会导致监督信息太少,但是增加有标签数据并不一定会增加有用信息,因此,需要分析有标签样本比例对性能的影响。
在表4 中的8 个数据集上进行实验,初始有标签比例取值范围为5%~50%,步长为5%,每个算法均运行30次,记录Accuracy的平均值。实验结果如图3所示,图中蓝色十字实线为STDPM算法的性能表现。
从图3 可以看出,当有标签样本比例小于20%时,在Banknote、Hepatitis、Ionosphere、Yale 数据集上STDPM 能获得较高的准确率,这是因为STDPM 能在有标签数据较少的情况下,利用密度峰值信息构造更接近真实数据结构的原型树,利用密度峰值隶属度选取出质量更高的样本添加进训练集。对于不同的有标签样本比例,在Breast、Palm 和Segment 数据集上各个算法的性能表现较为稳定,在Hepatitis、Ionosphere、Yale 和Zoo 数据集上,大部分算法的性能表现波动较大,而STDPM 在8 个数据集上的性能表现相较于对比算法更加平稳。
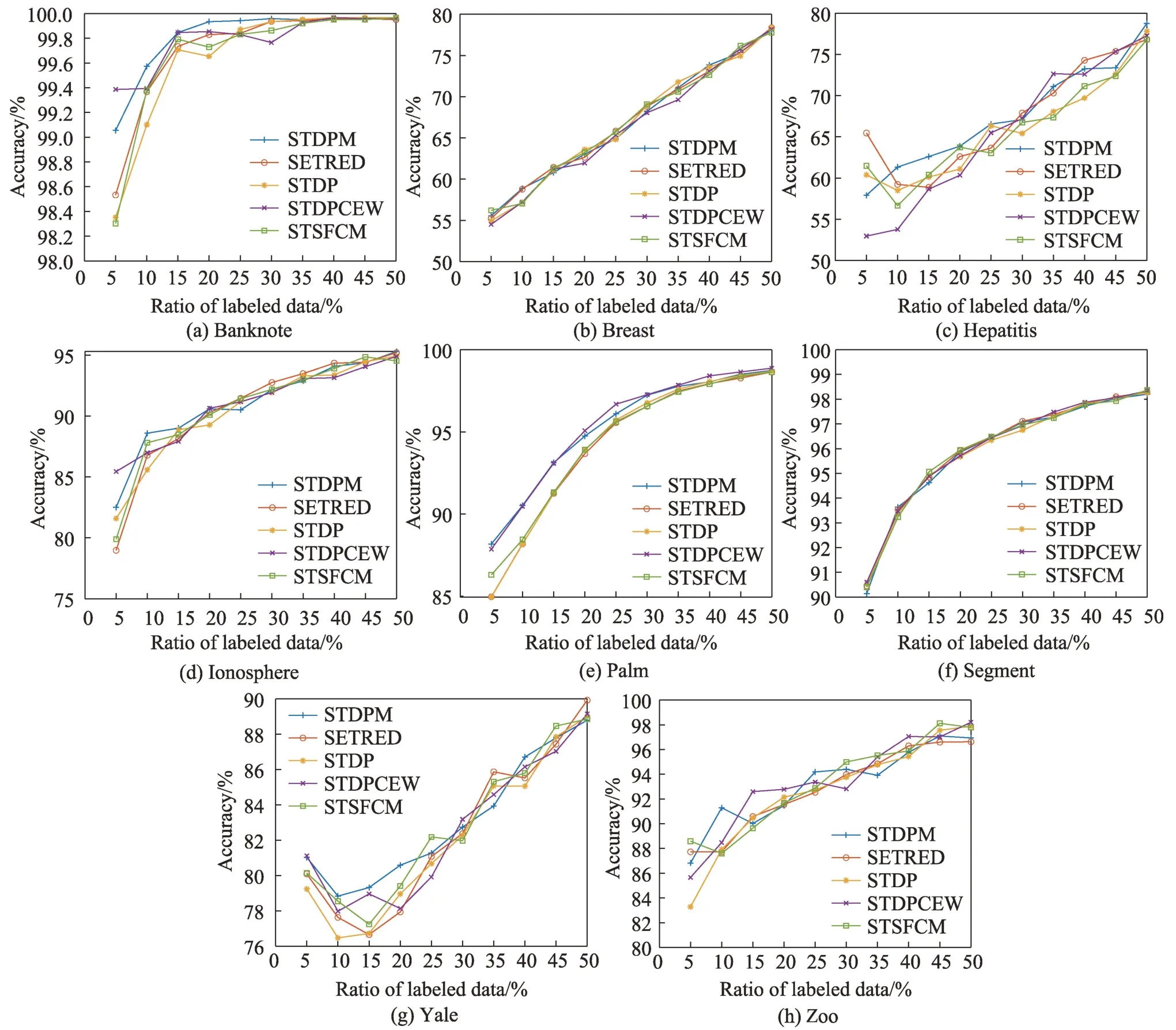
图3 不同有标签样本比例数据集上的准确率Fig.3 Accuracy on different ratios of labeled datasets
3.4 运行时间分析
表7 为5 个算法在8 个数据集上的平均运行时间(ms)和迭代次数,基分类器均为最近邻(NN),每个算法按照表3 设定的参数运行30 次。
由表7 可知,在样本量较多的Banknote、Breast、Palm 和Segment 数据集上,STDPCEW 算法的耗时高、迭代次数多,而SETRED 算法的耗时仅低于STDPCEW 算法但是高于其他3 个算法,因此,这两个算法并不适用于大规模数据。STSFCM 算法在7个数据集上耗时最低并且迭代次数较少,在较大的数据集上的耗时明显低于另外4 个算法,这是因为STSFCM 算法在不采用SVM 而采用NN 作为基分类器的情况下复杂度低于其他算法。STDP 算法在7 个数据集上的耗时仅高于STSFCM 算法,而STDPM 算法在7 个数据集上的运行时间略高于STDP 算法。由上述分析可知,STDPM 算法能以较少的迭代次数和较短的运行时间获得更高的分类性能。
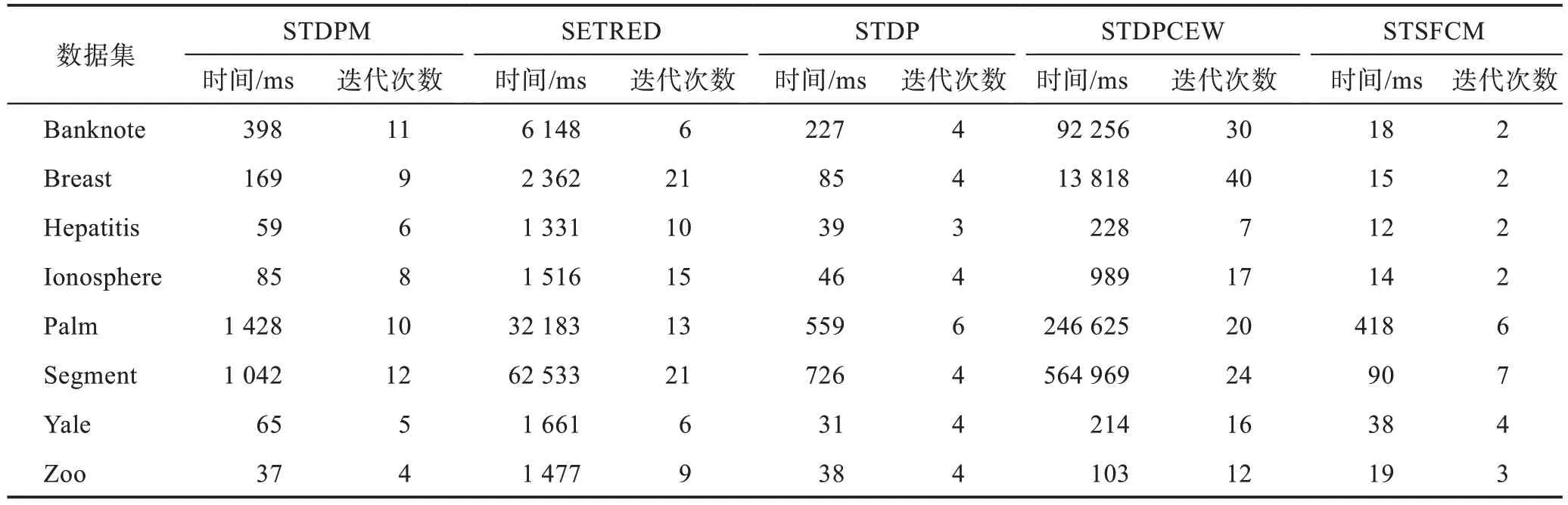
表7 运行时间对比Table 7 Comparison of running time
3.5 参数分析
STDPM 算法需要输入两个超参数:截断距离比例阈值和密度峰值隶属度阈值。取值的变化会影响截断距离的取值,使构造的原型树发生变化,最终对隶属度的计算产生影响。取值过大会导致类簇合并,取值过小会导致局部中心点过多,不合适的取值会导致原型树偏离数据的真实结构。
取值的变化会影响高置信度样本的选取,取值过大会导致迭代过程中选取高置信度样本过少,使迭代次数增加,取值过小会导致较低置信度的样本被添加进训练集,增加了误分类风险。
图4所示三维图展示了超参数和在不同数据集上的不同取值对准确率的影响,的取值范围为[1,10],步长为1,的取值范围为[0.1,1.0],步长为0.1。
如图4 所示,在8 个数据集上,取值小于5 能获得最高的准确率,在Banknote、Breast、Hepatitis、Ionosphere 和Yale 数据集上,取值较大时准确率较低,这是因为截断距离不合适,导致原型树不能反映真实类簇结构。因此,根据实验结果,的建议取值范围为(0,5]。在Banknote、Breast、Hepatitis、Yale和Zoo数据集上,取值小于0.5 能获得较高的准确率,在Ionosphere、Palm 和Segment 数据集上,取值大于0.5 能获得较高的准确率。由图4 可知,的合适取值取决于具体的数据集。
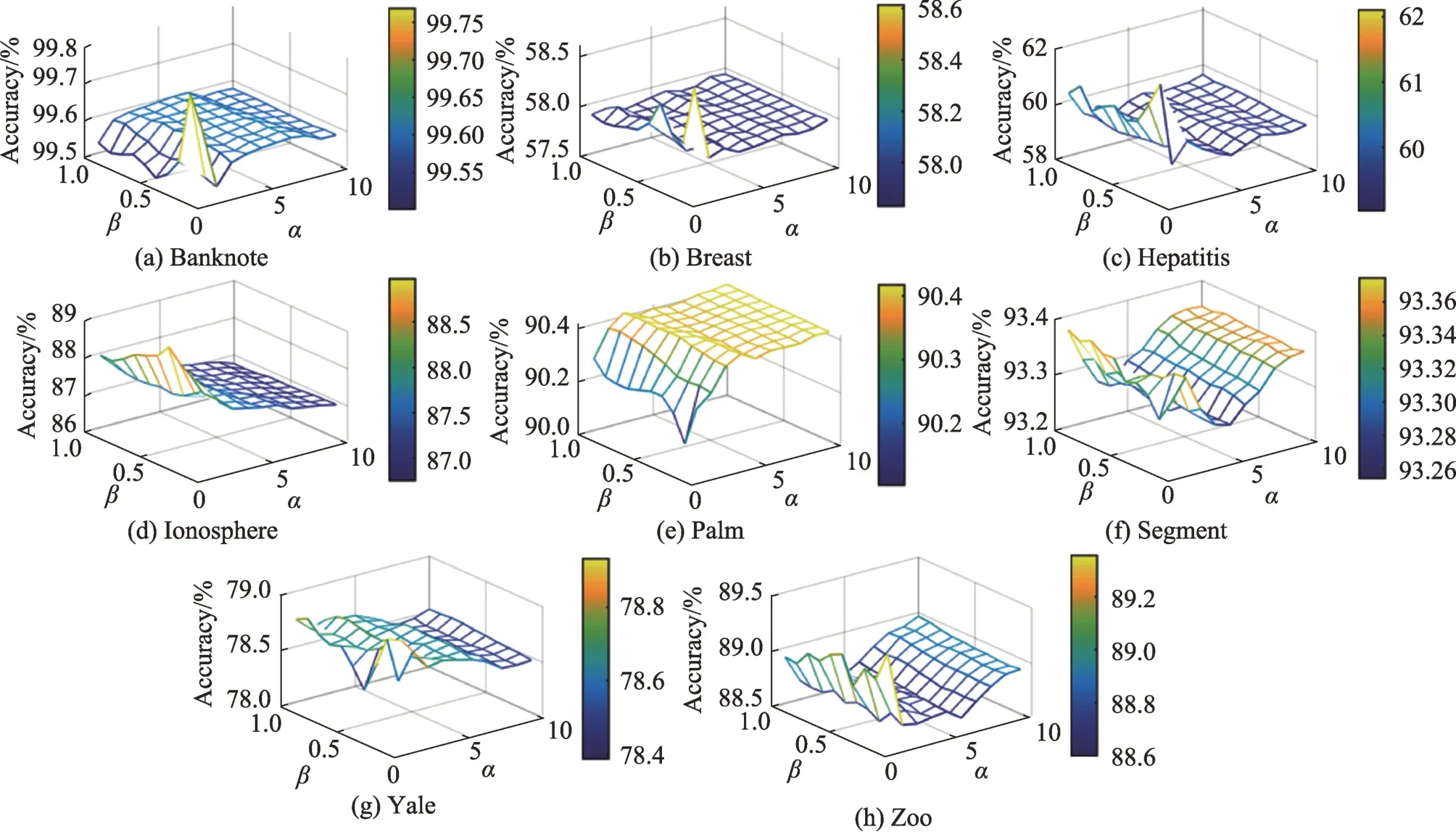
图4 不同参数α 和β 在不同数据集上的准确率Fig.4 Accuracy on different datasets with different parameters α and β
4 结束语
针对Self-Training 过程中高置信度样本选取问题,提出一种密度峰值隶属度优化的Self-Training 算法。首先利用密度峰值信息构造原型树,在原型树中搜索有标签样本的无标签近亲结点集。其次利用近亲结点集中无标签样本与每个类簇中有标签样本的簇峰值信息,计算密度峰值隶属度。最后设定密度峰值隶属度阈值,选取隶属度大于阈值的高置信度样本。在8 个基准数据集上的对比实验结果表明,STDPM 算法的分类性能优于对比算法,验证了利用密度峰值信息能更好地发现数据的潜在空间结构,利用密度峰值隶属度能选取更高质量的高置信度样本,从而提升Self-Training 算法的性能。
在今后的工作中,将在距离学习等方面更深入地研究密度峰值与原型树,重点探索更高效地发现高维数据、复杂数据的潜在空间结构的方法,并将其应用在半监督学习中。

