车铣复合直驱转台动静态特性优化设计
王俊雄,刘康,廖映华,胥云
(四川轻化工大学机械工程学院,四川宜宾 644000)
0 前言
车铣复合加工中心能实现多角度加工,满足多样化加工需求,不仅可缩短产品制造工艺链,提高生产效率,而且能减少装夹次数,提高加工精度。随着时代的发展,机械行业对加工精度的需求也越来越高,车铣复合加工中心在机械、航空、仪表、电子等工业中占有越来越重要的地位。
数控直驱转台作为车铣复合加工中心的核心部件,能够体现数控机床的高精度和高效率。它作为加工中心的第四或五轴对复杂曲面的加工具有十分重要的意义,不仅提高了数控机床的加工工件范围及精度,而且提高了数控机床的生产效率,因此国内外学者对它进行了大量研究。WHITTAKER和SADEK在优化设计前首先进行模型简化处理,实现在保持精度的情况下降低计算规模,从而降低计算量,节约了大量时间。目前对转台的优化设计方法主要是:对静态特性的对比优化,对动态特性的对比优化,结构拓扑优化和参数优化设计。周玲莉等利用多体动力学理论,建立了直驱转台的空间误差模型并进行了分析。胡秋等人以某型号高精度立式加工机床回转工作台为例分析了其关键技术,并提出了解决方案。苏彩虹建立了直驱转台的铣削动力学方程,并使用Deform-3D对仿真结果进行验证,为研究多个因素对切削力的影响提供了参考。李树宏通过分析直驱转台真实的铣削工况,并与VERICUT数控仿真结果相结合,检验了数控代码的正确性。栾强利等对数控机床直驱转台抱闸机构的工作原理进行分析,完成了多种抱闸机构设计。马进等人通过MATLAB的Simulink模块设计了满足光电子基片超精密抛光要求的转台系统。冯博、谢黎明等通过传热学理论对直驱转台进行了热分析,并提出了解决方案。上述文献对直驱转台加工精度、优化过程展开了分析,但是尚未发现利用直驱转台轻量化设计提高其加工精度的研究。
因此,本文作者以某型号摇臂式直驱转台为研究对象,将响应面法应用到直驱转台优化设计,建立较为准确的直驱转台模型,计算转台的加工力,并对转台进行动静特性分析,使用直驱转台的尺寸参数构建响应面并进行设计参数的灵敏度分析;利用NSGA-II算法对响应面进行优化得到Pareto解,重点解决直驱转台的轻量化设计,提高转台的动静态特性。
1 切削力计算
图1(a)所示为某型号车铣复合加工中心悬臂式直驱转台的剖分模型。
车铣复合转台的加工方式分为车削和铣削两种,其中车削时以轴带动工件旋转为主运动,刀具进行进给运动,实现对工件的切削加工。而铣削时,铣刀在电主轴带动下快速旋转,为主运动,工件在转台轴的带动下以较慢的速度旋转,并配合轴的摆动对工件进行加工。因为轴的运动原理与轴相似,故以轴为例,其受力分析如图1(b)所示。
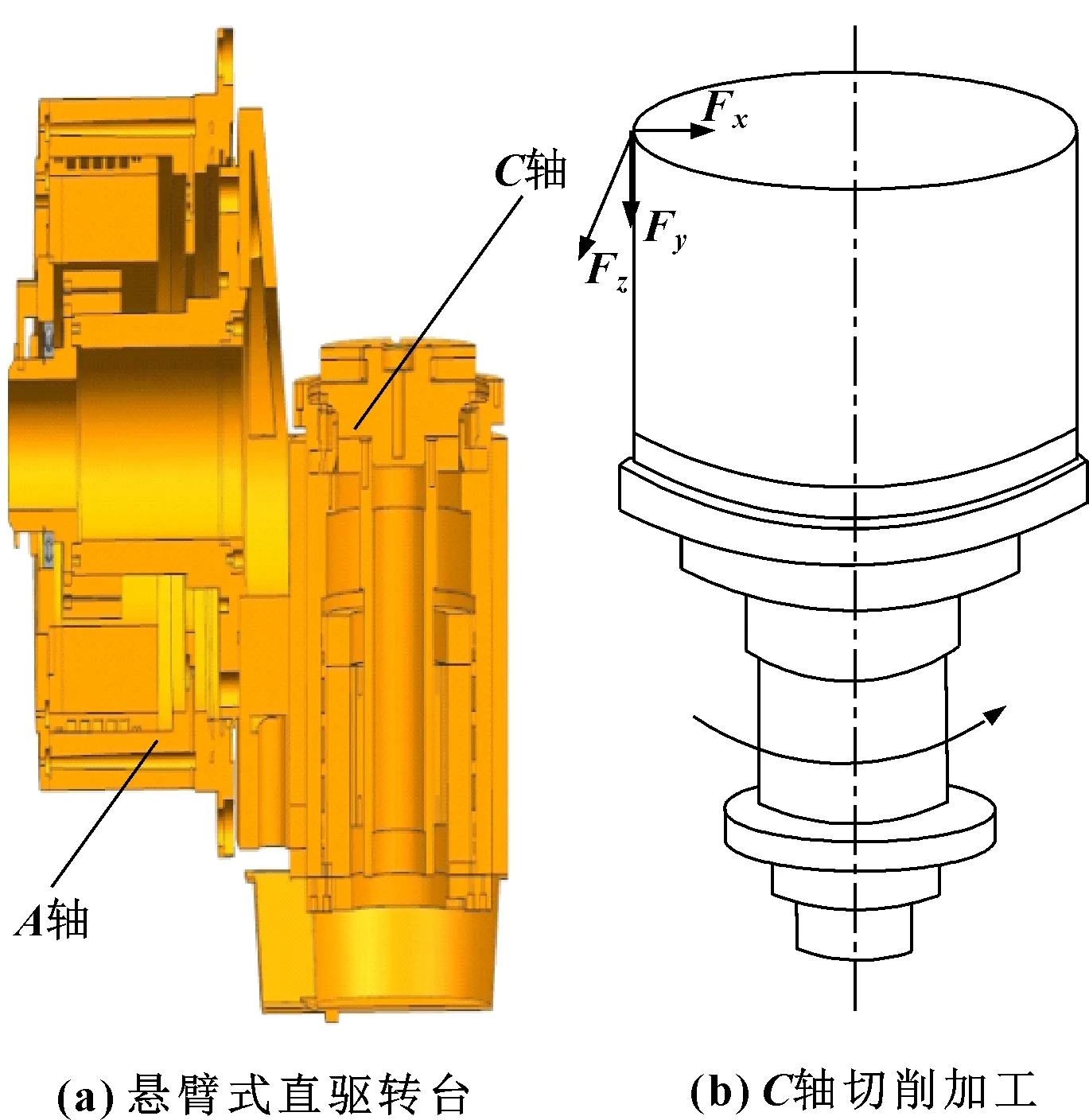
图1 直驱转台结构及加工示意
1.1 车削力计算
车削时,将车削力分解为3个分力,分别为主切削力、进给力、背向力,如图1(b)所示。
切削力为

(1)
由于工件为灰铸铁,根据切削实验确定的数据,刀具的主偏角=45°,刃倾角=0°,前角=10°,查询相关公式可以得到车削力的3个分力计算公式为

(2)
其中:、和取决于被切削金属和切削条件;、、、、、、、、分别为3个分力的背吃刀量、进给量、切削速度的指数;、和为3个分力的修正系数。
各系数如表1所示。

表1 在外圆纵车条件下切削力各参数系数
通过查询相关文献可知,在文中实验条件下,修正系数、和均为1.0。加工类型为外圆纵车,加工时背吃刀量为3 mm,每齿进给量为0.3 mm,切削速度为1.4 mm/s。
将切削参数代入到式(1),可以得到:
=1 097.53 N=577.18 N=836.36 N
1.2 铣削力计算
与铣削力相关的参数很多,如加工转台的铣刀类型、加工工件的材料、加工刀具的材料等。在铣削工况下与车削使用同样的刀具和工件材料,电主轴的功率为7.5 kW,额定转速为1 500 r/min,铣刀直径为63 mm,直驱转台的转速为200 r/min,铣刀长度=80 mm,铣削宽度=2/3,所以=53.3 mm。铣削方式为对称端铣削,铣削力可以用以下公式表示
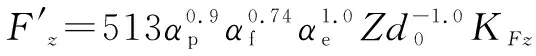
(3)
其中:为铣削深度,mm;为每齿进给量,mm;为铣削宽度,mm;为铣刀齿数;为铣削直径,mm;为修正系数。
刀具的齿数通过经验公式(4)计算
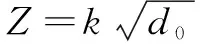
(4)
其中:为系数;为刀具直径,mm。端铣时各铣削分力的经验比值如表2所示。

表2 端铣时各铣削分力的经验比值
刀具采用螺旋齿铣刀,铣刀螺旋角=42°,=0.8,刀具直径为50 mm,齿数=6。
铣削宽度=0.6=30 mm,铣削深度=2 mm,每齿进给量为=0.15 mm,代入公式求得主切削力为

端铣采用对称端铣,各方向铣削力为
=09=761.895 N,=0.35=296.29 N,=0.52=440.20 N
2 直驱转台动静特性计算与分析
2.1 实体建模
由于直驱转台分析需要多学科知识结合,结构和驱动方法确定较为复杂,如果要建立真实的直驱转台模型非常困难,所以在建立实体模型时,必须进行必要的简化。简化的主要方法:(1)简化一些进行模型分析时可忽略的特征,如定位孔圆角等;(2)只分析比较关键的传动部位。因此,以车铣复合加工中心直驱转台的轴为例,使用UG简化并建立如图2所示的模型。

图2 直驱转台简化图
2.2 材料选择
转台面和工件使用的材料分别是HT200和HT250,安装套与旋转主轴使用45钢,YRT轴承材料为GCr15,具体参数如表3所示。
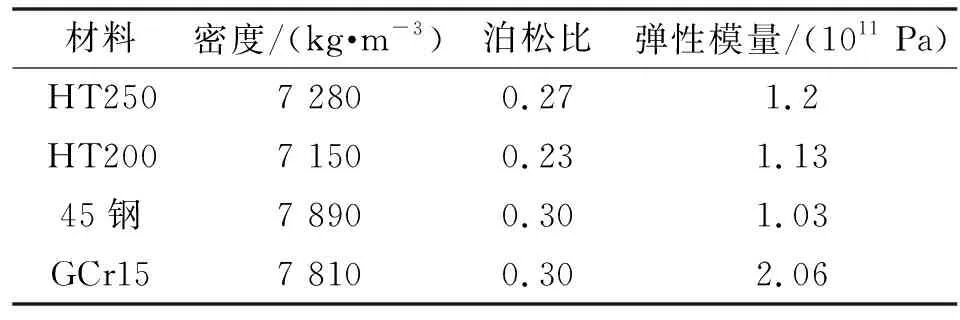
表3 材料参数
2.3 网格划分
利用有限元分析软件的自动划分网格功能对直驱转台进行网格划分,产生166 645个节点和67 418个网格。直驱转台网格划分如图3所示。
图3 直驱转台网格
2.4 静态特性分析
直驱转台的两种工作方式中,铣削对直驱转台的精度要求较高,故以铣削工况为例。
在直驱转台轴的转台轴承处添加固定约束,当铣削力添加在工件顶部的最大半径处时,不仅符合实际情况的加工条件而且能使工件和转台的变形和应力最大。铣削状态下其形变量如图4所示。
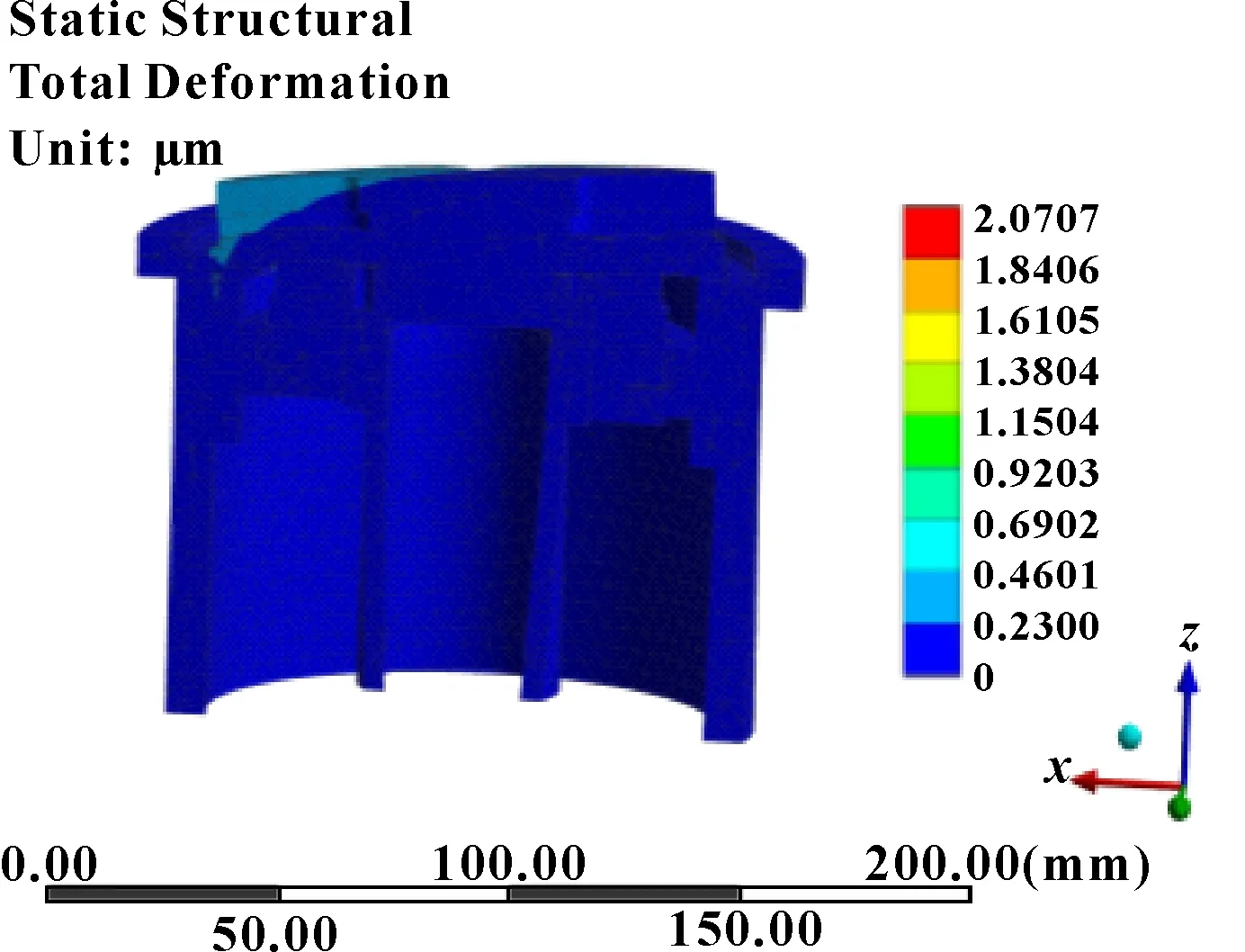
图4 铣削状态下的变形量
由图4可以得到:就刚度而言,在铣削工况下,其变形最大值出现在工件与刀具接触的位置上,约为2 μm;对于转台本体而言,其变形较小,主要分布在转台面边缘位置,约为0.36 μm。
2.5 结构动态特性分析
模态分析主要用于物体固有频率计算以及振型显示。固有频率是物体的固有特性,与物体的载荷无关。约束其安装套下部,对模型进行模态分析,得到前6阶模态如图5所示。对于一般物体,其第1阶模态在加工过程中最容易形成共振,所以在对物体进行模态分析时,应该重点关注其1阶模态。模态分析结果如表4所示。

图5 直驱转台的前6阶模态
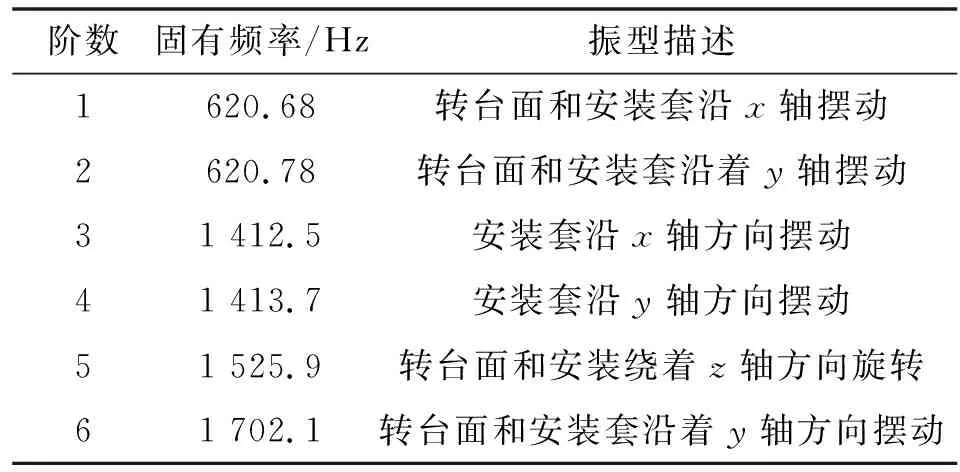
表4 模态分析结果
对比直驱转台轴工作参数,可以推断出转台的1阶模态满足要求。为防止直驱转台出现故障导致电主轴转速加快,在优化时应保证其1阶模态值不下降。
3 直驱转台的动静态多目标优化设计
未优化的直驱转台的轴质量为100.93 kg,铣削工况下加工最大变形为0.002 059 mm,1阶固有频率为620.68 Hz。为减少材料的浪费、降低转台工作时的刹车惯性及提高其加工精度,对直驱转台的动静态特性进行优化。
在优化之前需要选取直驱转台的优化目标、优化参数和约束条件。以工作台质量、1阶模态和刚度为优化目标,设置的约束范围为各优化参数的±10%,约束条件为不降低刚度和1阶固有频率,实现轻量化。
根据直驱转台结构,确定优化参数;采用UG对优化参数进行参数化设计。具体优化流程如图6所示。

图6 优化流程
3.1 直驱转台响应面设计方法
设计过程中选取6个优化参数,如图7所示。
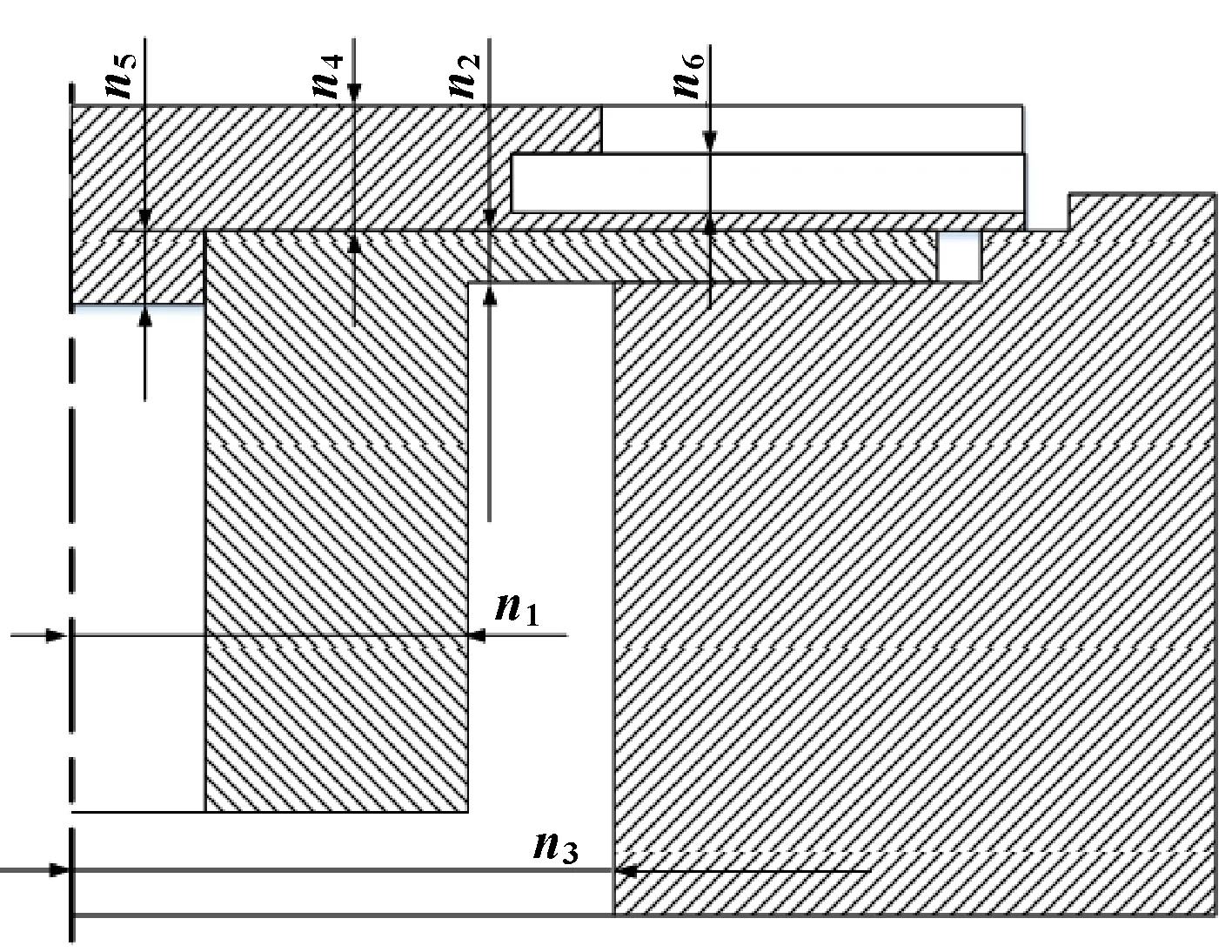
图7 直驱转台的设计参数
将这6个尺寸参数作为优化参数,设最大变形量、质量、1阶固有频率作为优化目标,可以建立如下优化模型:
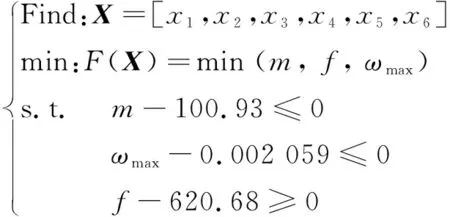
(5)
其中:为设计变量的向量;()为目标函数;为每个设计变量;为直驱转台的总质量,kg;为直驱转台在铣削工况下一阶模态,Hz;为直驱转台在铣削工况下最大的变形量,mm。
设计点的选取方法会极大地影响响应面的精度,实验方法的理论及选择可以通过相关文献进行查询,限于篇幅,文中不展开叙述。在响应面设计的过程中,需要选择响应面设计方法,此次实验采用中心复合实验设计(CCD)确定实验点。使用中心复合实验方法不仅能够保证精度,而且设计点的数量较少。使用CCD进行点的设计并计算出对应设计点的值,通过这些值来建立响应面模型。
响应面法是一种类似于拉格朗日展开式的全局性近似法,使用它解决多变量最优解的计算和分析问题。利用简单的数学模型来解决复杂问题,响应面法的数学原理如式(6)所示:

(6)
其中:代表所有设计点的集合=(,,…,);为CCD确定的设计点个数;为最小设计点个数,通过文献[17]可知=(+1)(+2)/2,在使用最小二乘法确定时,为CCD法确定的最小设计点个数,其设计点的数量必须大于。

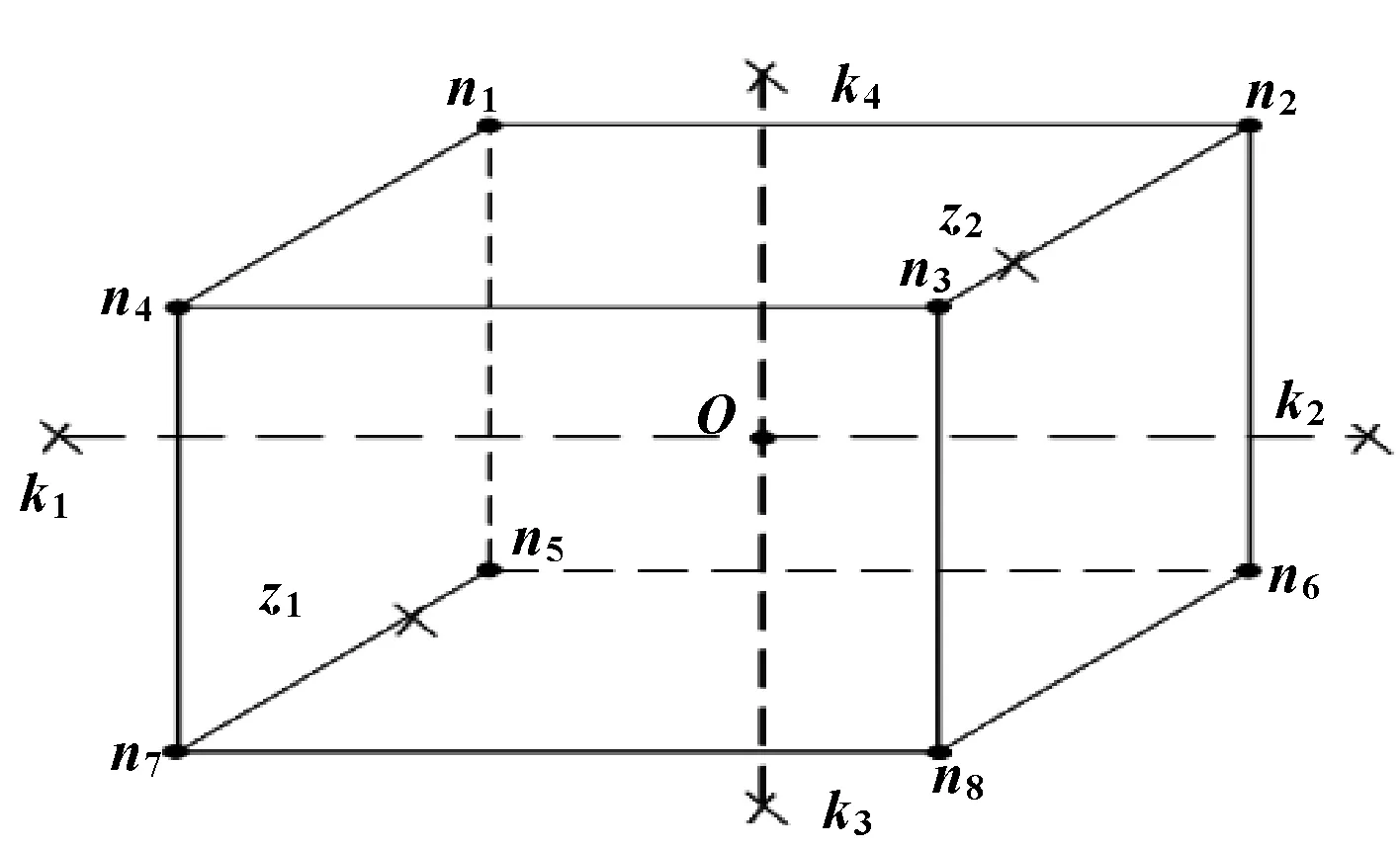
图8 CCD模型
通过有限元软件的优化功能得到了46个设计点,通过对设计点的计算构建响应面。由于参数值之间相差较大,采用归一法统计数据,可以较直观地得到优化参数~取值对优化目标的影响程度。刚度、频率和质量随优化参数的变化曲线如图9所示。
由图9可以看出:设计点与转台的1阶固有频率、刚度和质量均有关系,但是其相关性呈不规则分布。综合考虑上述参数与目标的关系,不能单纯地增大或减小单独参数来提高直驱转台的动静态特性以及降低其质量。由于所有优化参数很难同时达到最优,需要进一步进行多目标优化,以取得最优值。

图9 直驱转台响应面模型
3.2 转台的灵敏度分析
为方便优化过程,可以对直驱转台灵敏度进行计算,考察6个设计参数,计算出对转台质量、频率和刚度影响较大的参数。然后,对这些影响较大的参数进行重点关注,以避免无目的性的结构修改,最快、最好地进行结构设计,快速优化动静特性。灵敏度的理论依据可以用下式来表示:

(7)
其中:()为可导函数;为灵敏度。
通过对6个变量进行计算,得出对于转台质量、刚度、频率的灵敏度,结果如图10—图12所示。

图10 频率灵敏度相关性 图11 刚度灵敏度相关性
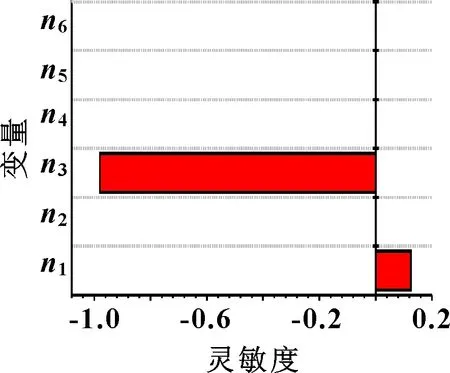
图12 总质量灵敏度相关性
由图10—图12可知:对频率敏感的参数为、和且均为负相关;对变形敏感的参数也为、和,均为正相关;对总质量敏感的参数为和,其中为正相关而为负相关。
3.3 优化结果
重点关注参数、、、和,使用有限元软件的响应面优化设计模块,将最小化转台质量、最大化1阶固有频率和最小化变形作为目标,使用多目标遗传算法(MOGA)取得3组Pareto的最优解。
传统的多目标优化方法是将多目标优化转化为单目标优化进行求解,但是传统求解的方法计算效率低而且不易得到全局性的优化解。因此,提出使用多目标遗传算法解决实际问题。由于各目标之间在优化过程中很难同时达到最优,多目标优化常常产生一系列有效解,也叫做Pareto解。就目标函数而言,这些解之间是无法比较优劣的,求解多目标优化问题就是无偏好地找到尽可能多的具有代表性的符合要求的Pareto最优解,在计算得到均匀分布的Pareto最优解之后,根据设计要求和工程实际经验,客观地选择最优的优化结果。NSGA-II被认为是最有效的多目标遗传算法之一,可以降低计算规模且可保存有效精英和种群的多样性,优化前后选取的优化尺寸参数、目标函数变化分别如表5、表6所示。

表5 原始参数及优化尺寸参数 单位:mm

表6 优化值及原始数据
由于质量占直驱转台优化权重最大,故选择优化值1为最优解。优化后质量降低了6.87%,1阶固有频率提高了2.28%,相同载荷的情况下变形量降低了1.99%,优化后优化目标均优于初始值,达到了优化的目的。
4 结论
通过分析该型号直驱转台的结构,以经典的铣削理论为基础,建立了该型号直驱转台的铣削模型,确定在铣削工况下的轴向力、径向力和切向力并使用有限元软件进行仿真分析,得到直驱转台在铣削工况下的前6阶固有频率以及刚度。在此基础上,为在保证直驱转台动静态特性满足加工要求的情况下实现直驱转台的轻量化设计,选取6个直驱转台上的优化参数,并将直驱转台的1阶模态、质量和刚度作为目标函数,使用有限元软件的优化设计模块对直驱转台进行优化。结果表明:优化后的直驱转台不仅具有更好的动静态特性,且质量下降了6.87%,能够更好地适应加工需求。

