基于光滑急动S曲线的激光钢坯标识机构轨迹规划
赵忠祥,潘存海,张帅鹏,李嘉文
(1.天津科技大学机械工程学院,天津 300222;2.天津市轻工与食品工程机械装备集成设计与在线监控重点实验室,天津 300222)
0 前言
传统的钢坯标识设备主要有撞号机、涂料喷涂标识设备、电弧喷涂设备和高能束喷涂标识设备等。而激光直接零部件标识(Laser Direct Part Marking)技术是一种在工业环境中证实可行、可实现高度自动化且绿色环保的标识技术,已经成为工业产品追溯中产品标识的重要手段。新型钢坯标识设备以多轴机械手为传动机构、激光打标机为核心部件对钢坯进行准确标识。
根据标识运动过程的不同,标识模式分为固定标识和飞行标识。固定标识即将标识设备运动到某一点后进行静态打标,要求运动结束后标识设备定位准确,并且残余振动小、在运动结束后能立刻进行标识而不需要额外的等待时间。飞行标识是标识机构在运动过程中对多个分立的产品进行动态打标,要求飞行过程中,标识机构快速进入运动平稳阶段,没有晃动,因此需要快速达到匀速段,即要求加速和减速时间短。同时,要保证机构运动过程中急动曲线的连续,以免产生较大的启停振动,但倍福PLC内置的梯形加减速曲线明显不能满足上述要求。因此,基于倍福PLC开发适合钢坯标识过程的轨迹规划算法很有必要。
标识机构轨迹规划算法直接影响最终的标识结果。梯形速度剖面虽然可达到时间最优,但它在理论上具有无限大冲击峰值的缺点,并且加速度曲线并不连续。S速度剖面曲线被限制在有限的加速度和冲击范围内,冲击曲线不连续,容易在结束位置产生残余振动。而高阶多项式S曲线、正弦S曲线和谐波S曲线具有连续且光滑的急动曲线,能保证开始和结束时刻急动值为0,即残余振动更小,适合此研究平稳、准确的要求。
本文作者介绍激光钢坯标识机构的运动学模型,比较正弦和谐波2种不同类型急动剖面的特点;给出谐波AS曲线的时间参数确定算法,并引入加速段和减速段的比率参数以简化模型;进一步比较两类存在匀速段的正弦S曲线,以找出匀速段占比更大的适合飞行标识任务的曲线类型;给出PLC程序数据转换时对精度的三次补偿策略,并在直角坐标机械手上进行试验验证。
1 直角坐标机械手运动学建模
采用滚珠丝杠结构将直角坐标机械手3个关节的平动转换成3个伺服电机的转动,并通过倍福PLC带动伺服驱动器进行运动控制。其运动学模型如图1所示。固定标识时3个轴同时运动,在对每个轴分别进行轨迹规划后需要进行三轴同步,以保证同时到达指定位置。激光打标器有一定的标识工作范围,因此在飞行标识时应保证激光打标器与钢坯端面距离恒定。基于上述任务要求,飞行标识时轴1运动到方向某一位置后,轴2、轴3同时运动,带动安装在工具坐标系的激光打标机对平面上多个钢坯端面进行平动标识。
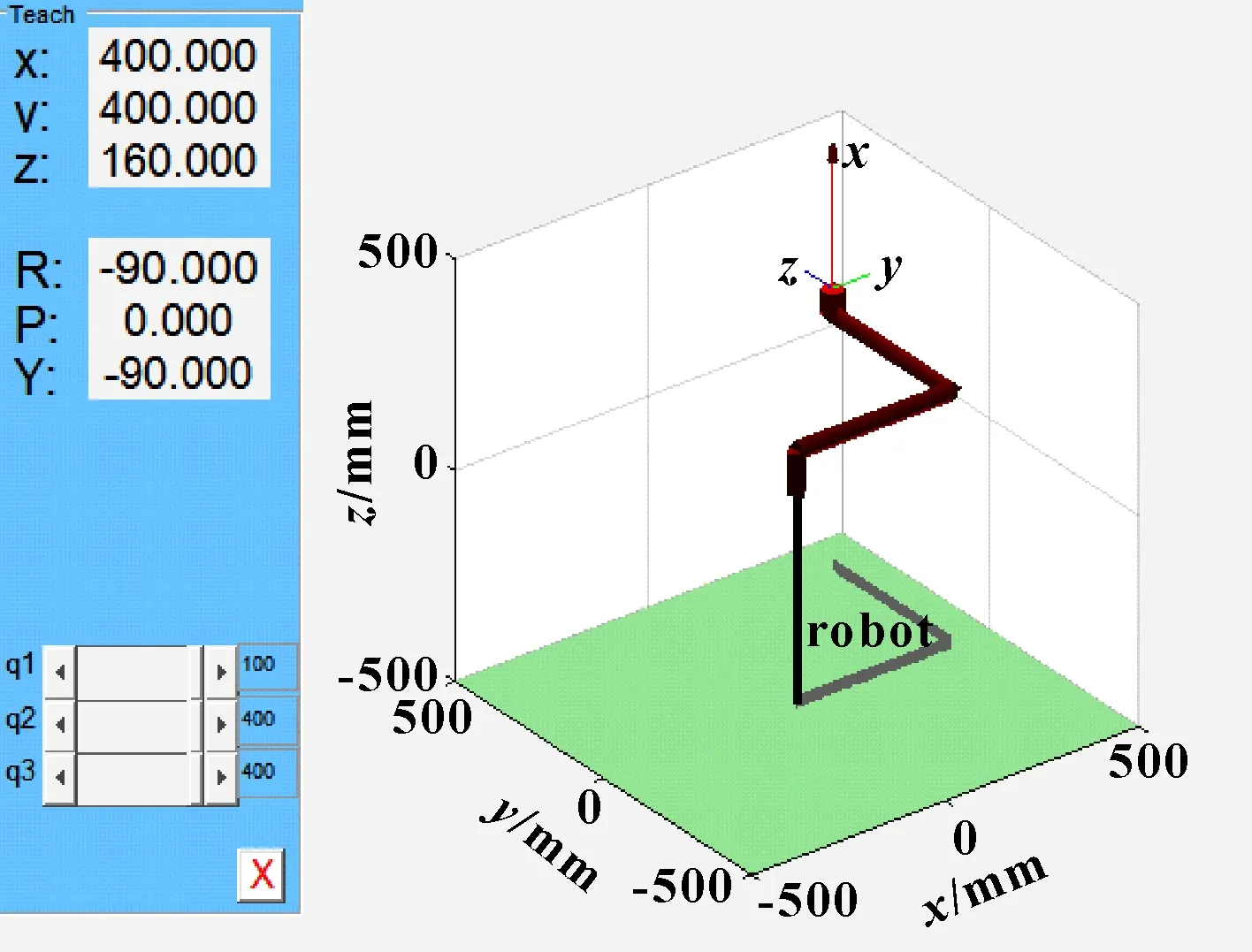
图1 直角坐标机械手运动学模型
2 正弦和谐波急动轮廓比较
正弦和谐波S曲线不仅克服了高阶多项式S曲线表达式复杂、难以实时进行运动控制的缺点,同时具有曲线无限可微、急动轮廓与高阶多项式S曲线急动轮廓一样光滑的优点。典型的正弦和谐波S曲线急动轮廓的表达式分别为
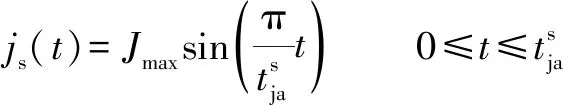
(1)
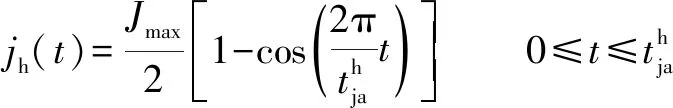
(2)
如图2所示,正弦和谐波S曲线的急动轮廓具有不同的分布特性,因此得到的轨迹规划曲线适用于不同的运动场合。
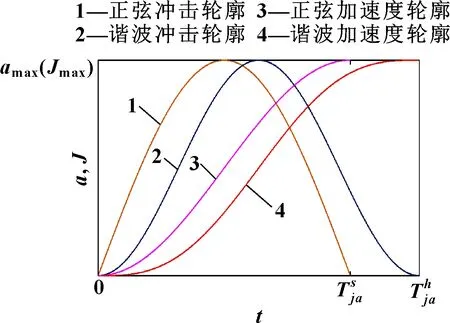
图2 正弦和谐波S曲线冲击轮廓比较
由图2可知:当两种曲线以相同的急动限制值达到相同的加速度限制值时,显然谐波S曲线更加平缓但付出了更多的运动时间和运动距离。因此谐波S曲线更适合于要求启停平稳尤其是停止时残余振动小的固定标识任务,而正弦S曲线适合于要求有较小加速、减速时间和距离的飞行标识任务。
3 谐波AS曲线的时间参数确定
为获得具有低残余振动强度的精确定位,期望执行机构具有快速启动和缓慢、平滑的停止。因此,在设计具有这种运动学特征的输入时,需要不对称的速度剖面。典型的不对称谐波AS曲线如图3所示,轨迹规划重点在于在给定的运动学约束范围内合理规划各时间段参数以及找出产生各类曲线的位移边界值。为简化轨迹规划模型,引入加速段和减速段的比率参数,其中、、和中有3个独立参数和1个相关参数,相关参数可由独立参数确定。

(3)
(1)能达到速度最大值,同时达到加速度最大值和时,则有:

(4)
其中:能达到这种情况的最小位移
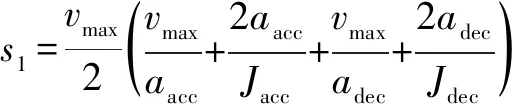
(5)
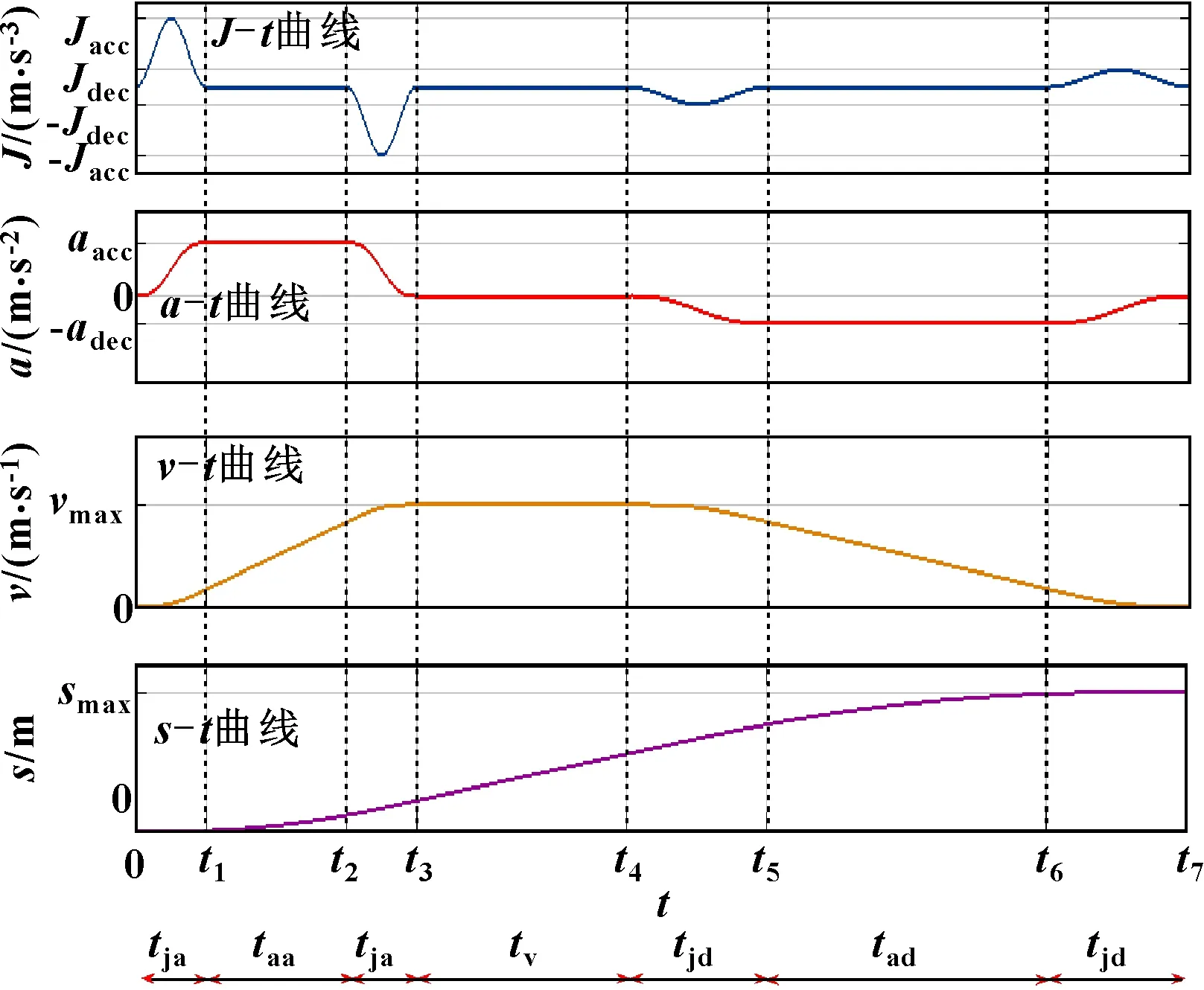
图3 不对称谐波AS曲线
(2)不能达到速度最大值,能达到加速度最大值和时,则有:
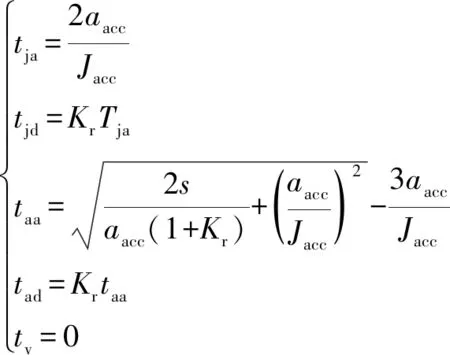
(6)
其中,能达到这种情况的最小位移值
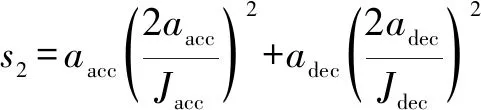
(7)
(3)能达到速度的最大值,不能达到加速度最大值和时,则有:
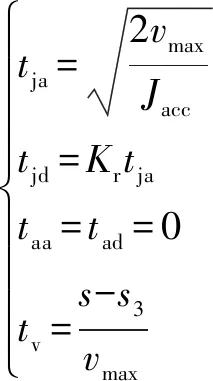
(8)
其中,能达到这种情况的最小位移值

(9)
(4)不能达到速度的最大值,不能达到加速度最大值和时,则有:
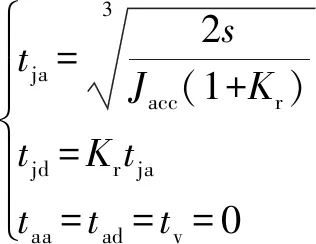
(10)
为保证所有轴同时到达目标位置,需要以最慢的轴为基础进行时间尺度同步。=max{,,}为3个轴中的最大运动时间。除最慢的轴外其他两轴需要重新进行运动学参数限制。同步因子利用式(11)进行计算,同时重新生成的运动学参数允许值由式(12)确定。
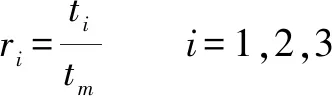
(11)

(12)
4 正弦S曲线类型选择及参数确定
激光器的标识工作状态应处于匀速以确保在相同时间延迟后达到下一钢坯端面的相同位置进行打标,如果速度变化会导致每个钢坯端面的标识位置不同,甚至不能成功打标。因此,轴2和轴3应在同一时刻开始和结束匀速段。
与谐波S曲线类似,正弦S曲线同样由于运动距离的长短会产生4种不同情况。考虑存在匀速段的2种情况,如图4所示。时间参数的确定与第3节谐波S曲线类似,此节侧重进一步比较2种情况的匀速段在整个运动过程中的占比,以选择匀速段占比更多的曲线类型。

图4 存在匀速段的2种正弦S曲线
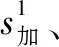

(13)
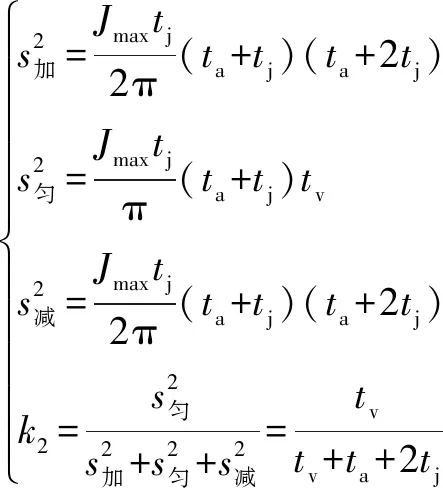
(14)
显然,在各时间段取值相同的情况下>,即不存在匀加速度段正弦S曲线的匀速区间在整个运动过程中的占比更大,所以飞行打标过程的运动曲线选择不存在匀加速段的正弦S曲线。激光飞行打标机构运动精度取决于直角坐标机械手轴2和轴3各自关节空间运动合成笛卡尔空间运动后的精度。它要求轴2和轴3在同一时刻开始和结束匀速段。考虑对排列在斜面上的圆钢端面进行标识,设斜面倾角为,则轴2关节空间的位移和轴3关节空间的位移有以下关系式:
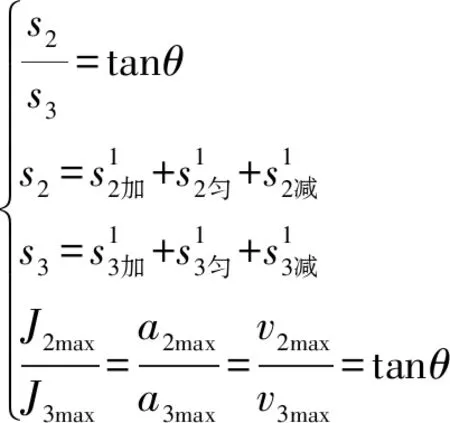
(15)
5 三次精度补偿
在实际工程应用中,上述算法都需要经过离散化才能在数字控制器上实现。因此,必须将、和全部转化为系统采样周期的整数倍,以保证同步、提高精度。以第3节的谐波AS曲线为例进行说明,值得注意的是此补偿方法对第3节的4种情况都适应。
(1)根据给定约束条件,按照第3节算法计算各时间段、和的值,转换为采样周期整数倍后如式(16)所示,其中[]表示不超过某个数的最大整数,为采样周期。

(16)
将重新计算后的、和代入算法得到补偿前的位移和能达到的最大速度。与目标位移之间的差值通过增加最大速度的持续时间进行第一次精度补偿。则需要增加的最大速度持续时间为
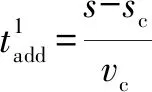
(17)
转换为采样周期的整数倍后:

(18)

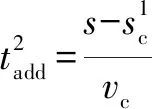
(19)
转换为采样周期的整数倍后:
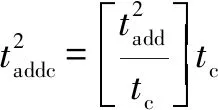
(20)
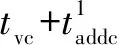
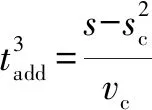
(21)
转换为采样周期的整数倍后:

(22)
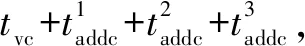
6 试验验证
在基于倍福PLC搭建的直角坐标机械手上分别对第3节和第4节的两类曲线进行试验验证。以在平面上运动的轴2和轴3为研究对象,谐波AS曲线在两次不同运动学参数限制条件下的运动曲线分别如图5—图8所示。正弦S曲线在达到最大许用运动学限制的条件下刚好能产生匀速段的极限运动情况,如图9和图10所示。当进一步提高运动距离或降低急动、加速度限制值时匀速段持续时间将会增加。
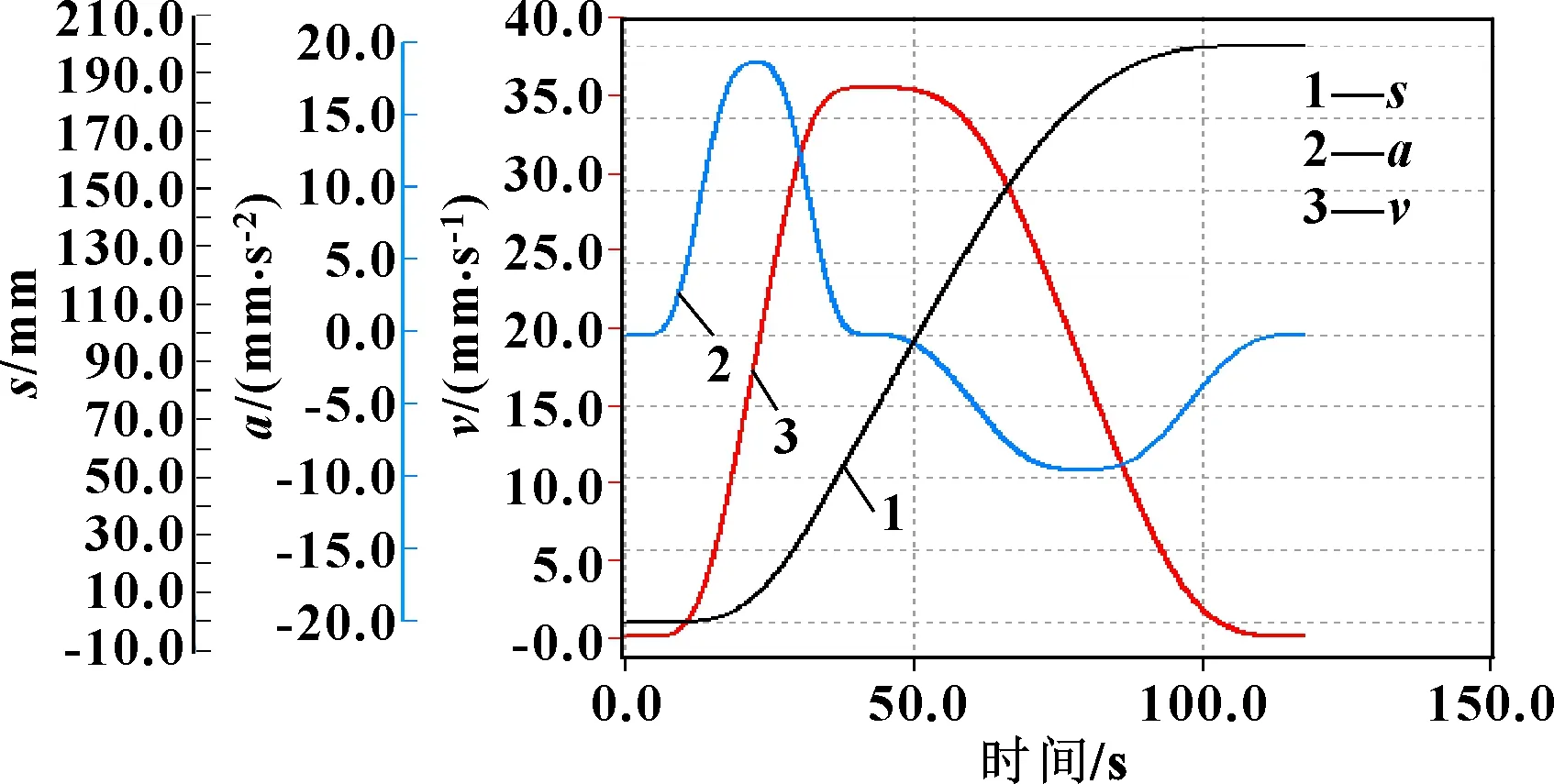
图5 第一次试验时x方向轴2的运动曲线(不能达到速度和加速度许可限制值)

图6 第一次试验时y方向轴3的运动曲线(能达到速度许可限制值,不能达到加速度许可限制值)
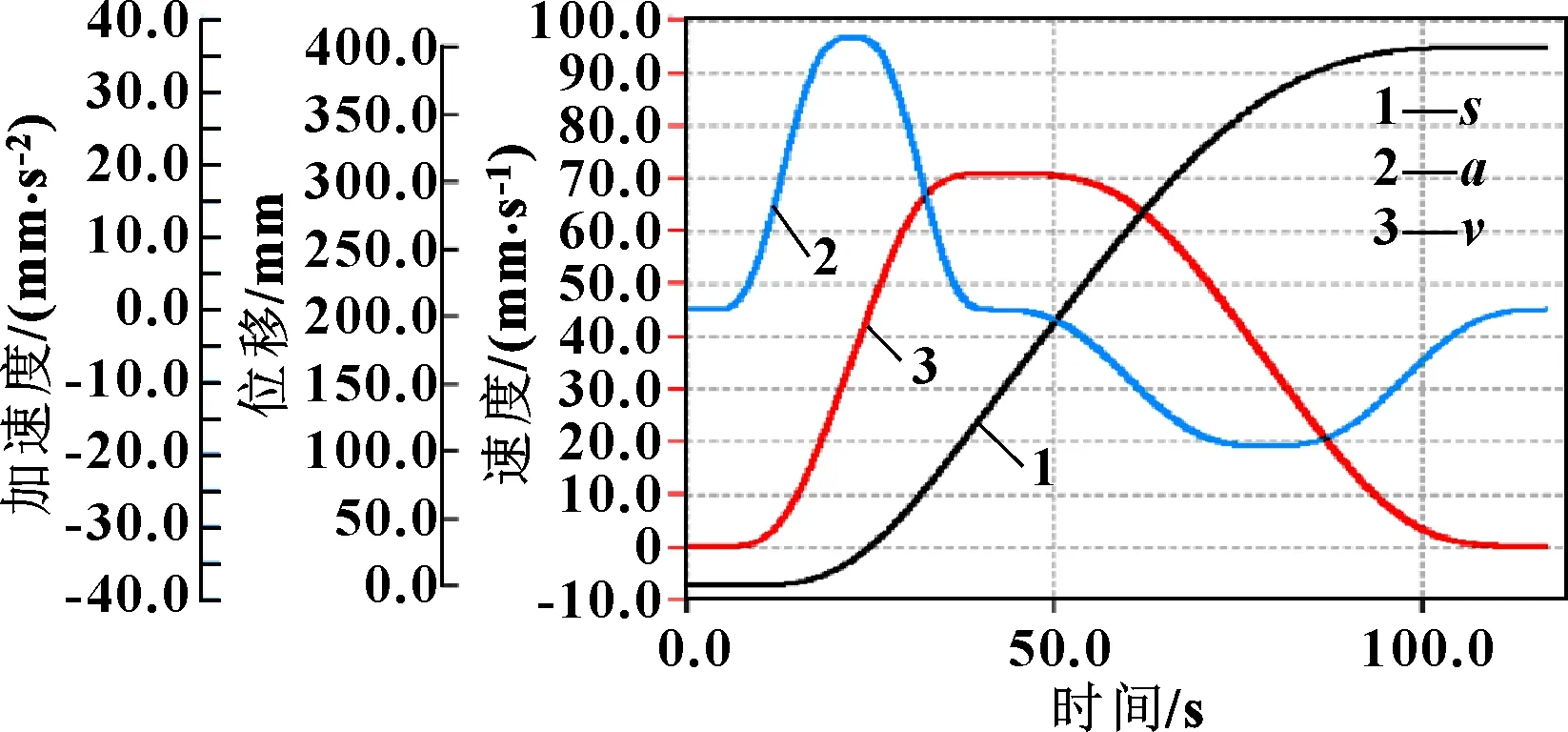
图7 第二次试验时x方向轴2的运动曲线(不能达到速度和加速度许可限制值)
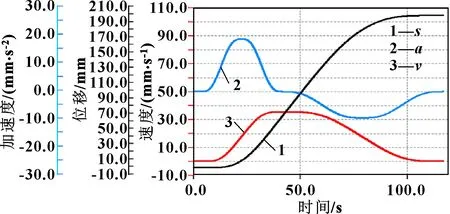
图8 第二次试验时y方向轴3的运动曲线(不能达到速度和加速度许可限制值)
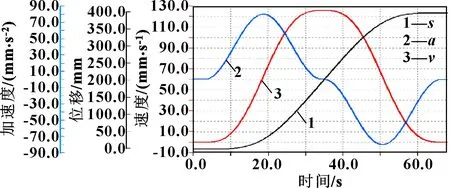
图9 x方向轴2能产生匀速段的极限运动情况

图10 y方向轴3能产生匀速段的极限运动情况
试验结果表明所设计的谐波AS曲线和正弦S曲线在直角坐标机械手上运行状况良好,能满足激光钢坯标识过程中不同标识任务的要求。
使用不同的运动学限制进行多次试验,前两次试验时轴2和轴3精度补偿前后的终点位置如表1所示,多次试验后补偿前后的相对位置误差如图11所示。显然,进行三次精度补偿能有效缩小与目标终点位置之间的相对位置误差,验证了三次精度补偿算法的有效性。
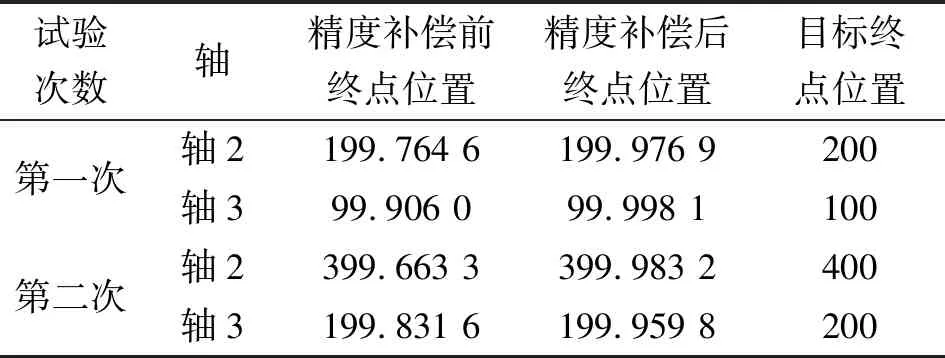
表1 谐波AS曲线三次精度补偿的试验验证 单位:mm
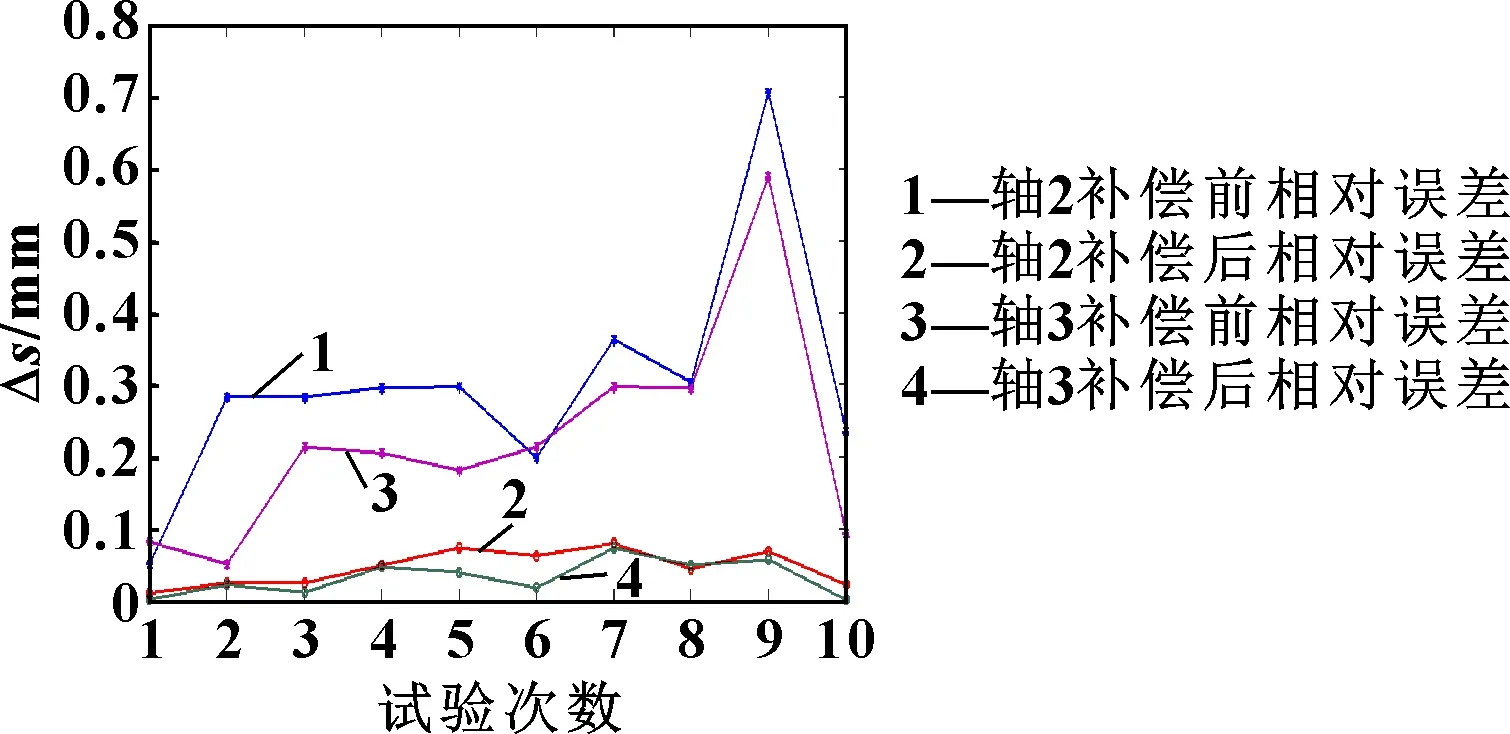
图11 轴2和轴3精度补偿前后的相对位置误差
7 结论
本文作者以运动平稳、精确为目标对激光钢坯标识设备运行过程中的固定标识、飞行标识两种不同的标识类型进行轨迹规划。
(1)成功开发出了替代PLC内置梯形加减速的光滑急动S曲线运动控制功能块。使用该功能块时只需在对应的输入接口处填写运动学约束,即可得到规划好的运动轨迹曲线。
(2)对PLC在数值转换过程中引起的精度损失进行三次精度补偿,通过增加匀速段运行时间对产生的位置误差进行补偿。
试验结果表明:标识设备各轴运行过程平稳,经过补偿后的终点位置准确。研究成果也可应用于高精度机床的平稳启停和精确定位场合中。

