跨座式单轨弓网耦合鲁棒主动控制策略

刘朝涛,蓝立俊，杜子学，杨震

(重庆交通大学机电与车辆工程学院，重庆400074)

0 前言

重庆市跨座式单轨列车属于城市轨道交通的一种新型形式，对于其他制式的轨道交通，跨座式单轨交通有其独特的机械结构和驱动原理。跨座式单轨列车随着运行速度的增加，弓网之间容易产生振动以致接触力大幅波动。接触力过大容易使弓网间的摩擦增大，造成设备间磨耗加剧，严重时会出现其他安全事故；过低的接触力容易造成弓网分开的离线现象，所产生的电弧和火花对相关的电气器件会产生烧蚀，对信息通信造成干扰。因此，对于受电弓进行主动控制以降低接触力波动具有很大的意义，同时也是轨道交通电气化发展不可或缺的一部分。

基于跨座式单轨列车的设计特殊性，国内外对于单轨受电弓的研究不是很多，但是对于高速铁路受电弓的主动控制已有大量的研究，所以文中借鉴了高速铁路受电弓主动控制的研究方法。文献[2]提出了一种基于估计器的主动双受电弓H控制策略，在得到受电弓状态的基础上，用了一种鲁棒递推状态估计方法，可以有效地处理随机缺失测量，以减小接触力波动。文献[3]采用了滑模鲁棒控制来调节弓网的接触力，其中设计的滑动模态控制器是基于输出调节问题的标准滑模控制理论，最后通过仿真实验验证了设计的方案。文献[4]研究了一种多目标鲁棒主动控制方法，分析引起接触力波动的因素，以确定3个控制目标，即最小化集电弓收集器的加速度，限制控制力和位移约束，最后验证了其方法的可行性。文献[5]提出了一种基于模糊滑模控制器和附加补偿器的高速列车受电弓接触网鲁棒控制方法，控制采用了PID外环反馈，然后由模糊系统在线调节滑模项和PID项的增益来控制接触力的波动，仿真结果与实际情况吻合较好。文献[6]提出了一种基于Pareto集和变权的受电弓主动悬架参数优化设计方法，采用约束多目标进化算法，通过大量的仿真验证了所提出的设计方案。

本文作者借鉴以上学者们的研究，针对跨座式单轨受电弓的特点，建立了一种主动控制模型，并提出了一种鲁棒主动控制方法。在跨座式单轨受电弓底座和框架间安装有升弓弹簧，为弓网间接触提供自适应力，但升弓弹簧响应非常有限。因此，需要加入执行机构进行主动干预和调节。文中所研究的主动控制是以直流电机为执行机构，为了不改变受电弓内部结构参数，所以将电机与框架连杆直连；并且希望在减少传感器数量的情况下，通过卡尔曼滤波算法获得精确度较高的电机转子状态控制信息；最后设计了鲁棒H控制器作为系统整体控制器。整体系统结构如图1所示。

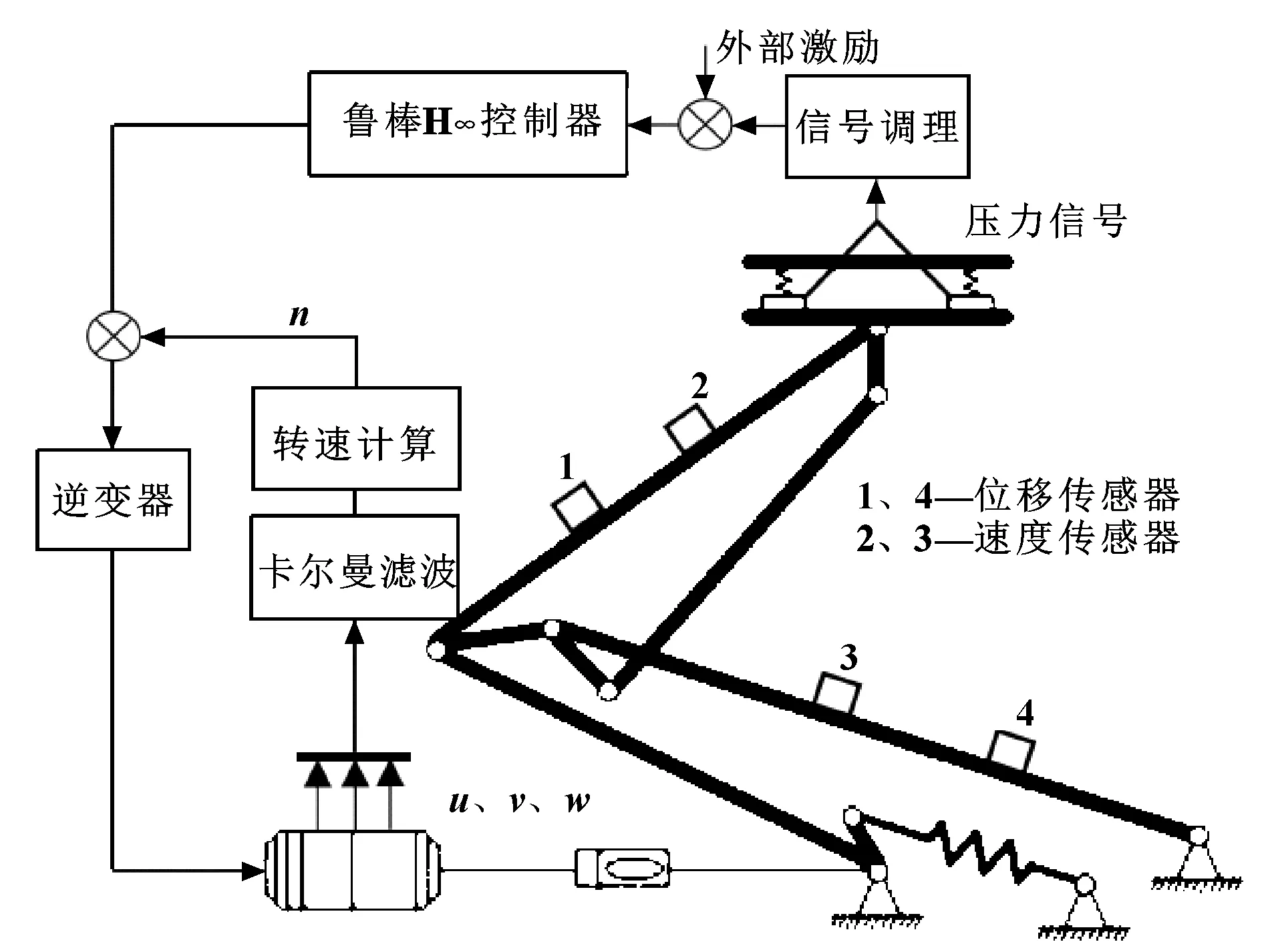
图1 系统结构

1 跨座式单轨列车弓网耦合模型

1.1 弓网系统耦合模型的建立

跨座式单轨受电弓主要由底座、框架、弓头以及受电弓弹簧等部件组成。单轨受电弓在结构上与其他制式的受电弓有较大的差别，但是在工作模式和动态特性上有相似之处。所以在分析单轨受电弓的动力学模型时，可以参照现有的方法进行。考虑到弓网动态耦合时，接触力的波动范围不大，因此，可以对受电弓的动力学模型进行线性化处理。

跨座式轨道交通弓网耦合系统不同于其他的轨道交通的弓网耦合系统，接触网是通过锚段关节连接每一段伸缩单元并固定在轨道梁的侧壁，而受电弓则是横向安装在轨道列车的底部裙板，弓网耦合系统为横向刚性接触受流。所以，重力和空气阻力都可以忽略不计。

由于弓网接触为刚性接触，理论上是不存在弹性形变的，但是在振动的影响下，接触线和汇流排的整体会产生一定的弹性变形，因此在建模时要考虑接触网的弹性特性。同时，为了方便建模，将支持绝缘子视为刚体，并且假设接触网每个跨距都是均匀的，且跨距之间的过渡段光滑无硬点。最后将受电弓框架部分以及弓头部分看作单独的质量块，它们之间以等效的刚度和阻尼相连，因此得到了简化的弓网耦合模型如图2所示。

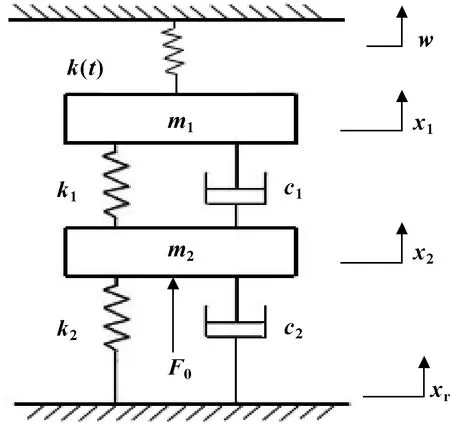
图2 弓网耦合动力学模型

可以得到弓网耦合系统的运动微分方程为

(1)

式中:()为接触网的等效刚度;为静态抬升力;为接触网不平顺以及振动产生的激励;为列车振动产生的激励。

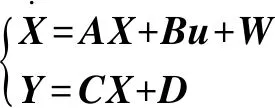
(2)

其中：

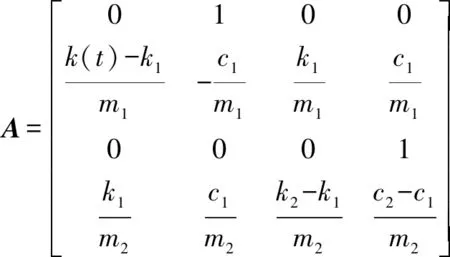
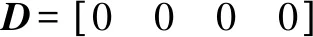
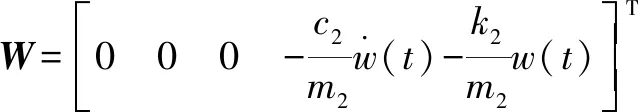
基于此，整个系统的问题可以转化为设计一个弓网接触力()反馈律的问题：

()=()

(3)

其中:是控制增益矩阵。受电弓的鲁棒控制问题是确定满足以下要求的控制增益矩阵：

(1)闭环系统是渐近稳定的；

(2)当外部扰动不大于时，控制目标得到保证。

1.2 弓网系统耦合模型的仿真分析

跨座式单轨列车的轨道由预应力混凝土梁组成，正、负的链节沿预应力混凝土梁的两侧刚性安装。由于跨座式单轨列车中特殊的受电弓与接触网之间的耦合关系，导致跨座式单轨还没有集电质量标准。但是根据铁路标准TB/T 3271—2011、重庆跨座式单轨运行的经验,以及杜子学团队对单轨受电弓所研究的结果，给出了跨座式单轨的集电质量参考标准。

跨座式单轨的受电弓与接触网之间的接触力在整个工作行程中应在44～79 N内。因此，受电弓与接触网的最大接触力应小于79 N，受电弓与接触网的最小接触力应大于44 N。 接触力的标准差直接反映了接触力的波动范围，标准差越小，接触力的波动范围越小，集电质量越好。

弓网系统中，静抬升力=100 N，升弓弹簧刚度和阻尼系数为=12 900 N/m、=100 N·m·s/rad;弓头支座的橡胶弹簧刚度和阻尼系数参数为=17 000 N/m、=200 N·s·m/rad,接触刚度为()=73 200 N/m,弓头以及框架的等效质量=2.354 kg、=10.647 kg；对于外部激励的功率参数可以参考日本刚性悬挂接触网不平顺功率谱密度函数。文中由此对弓网耦合模型进行了Simulink建模仿真，并且在40、60、80 km/h时速段进行了弓网接触力的时域响应图分析，如图3所示。

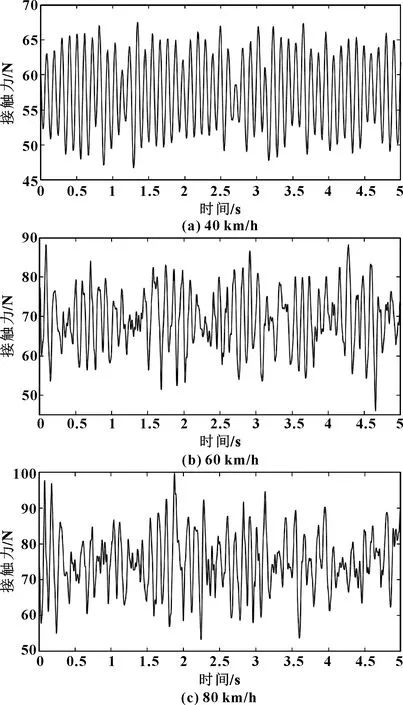
图3 不同时速下的接触力响应曲线

由图3分析可以统计出不同时速下的接触力，如表1所示。

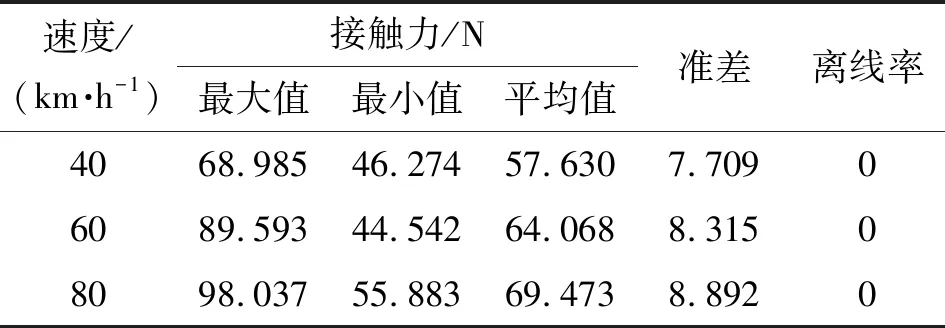
表1 不同时速的接触力数据统计

由图3可知：列车在40 km/h运行时，接触力的变化是比较平缓的，集中在45～70 N之间，受电弓属于最佳的受流区间；但是随着速度的增加，列车在60 km/h运行时，接触力的变化较为剧烈，大多数集中在50～85 N之间，脱离了受电弓最佳的受流区间；列车在80 km/h运行时，弓网之间的接触力变化最不稳定，所以需要在列车高速时对受电弓进行主动干预，让接触力的波动有所减小，以降低弓网接触力。

2 直流电机模型与控制器设计

永磁无刷直流电机在工业领域越来越受欢迎，因为与其他类型的交流和直流电机相比，它具有更高的功率密度、更简单的制造工艺、更低的生产成本和响应时间快等显著优势。

2.1 永磁直流电机模型的建立

标准的三相直流电机系统可以用方程在状态空间中表示：

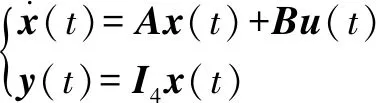
(4)

其中:是4×4的单位矩阵，其余变量为

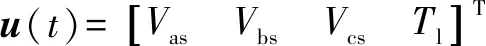
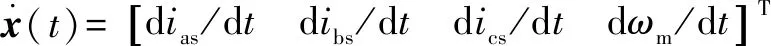
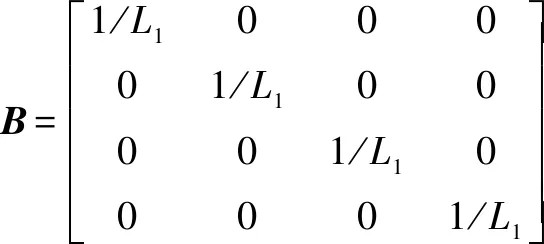
式中：、和是直流电机定子绕线的相电流；是角速度；、和是每相的电压输入；是机械负载的扭矩；是每相电阻；=-，其中是所有三相共有的每相自感，是相之间的公共互感；是转动惯量；是扭矩常数；是速度常数。永磁直流电机在三相之间以共同的电流和电压运行，即：===，===。

2.2 逆变器模型的建立

此系统采用H全桥作为三相逆变电路，它主要是由6个对称的MOSEFT管构成，如图4所示。

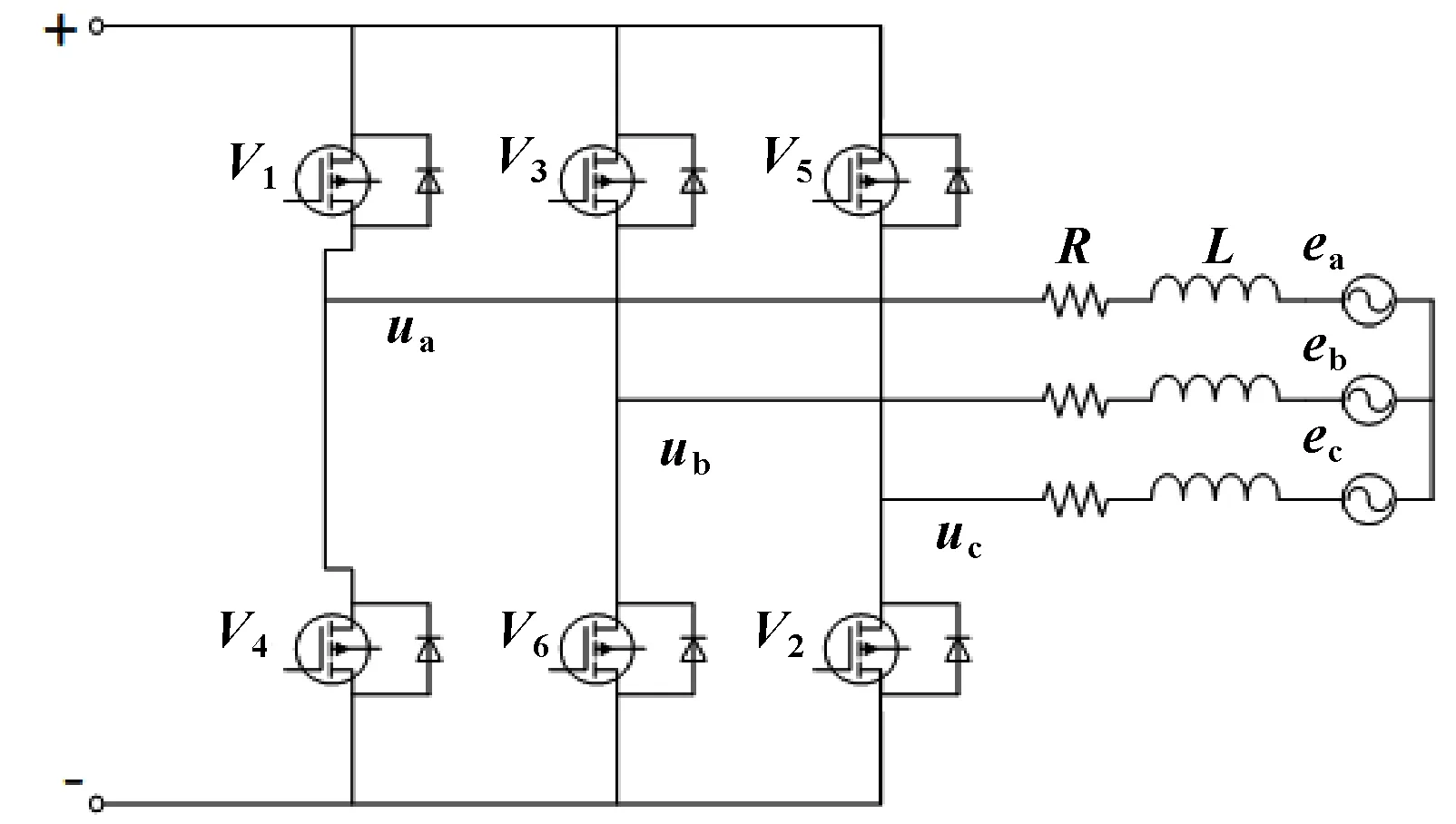
图4 逆变器拓扑

当直流电机ab相导通时，=0，可得：

(5)

电机在换向的时候，c相导通，不为0，会产生反向电动势，则：

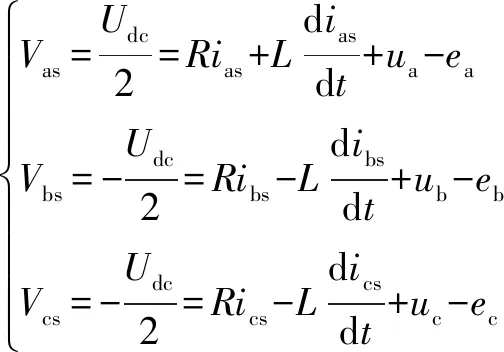
(6)

是直流侧的电压，通过逆变器，结合电感电动势可以得到输出至三相绕组的端电压。

2.3 卡尔曼滤波算法

电机在换向时存在反向电动势会产生系统频率噪声，这对电机的响应时间有影响,于是文中提出一种卡尔曼滤波算法来实时检测电机转子的位置以调整电机的响应时间。该算法是根据电机主动控制系统中容易得到的相电流和相电压等信号，利用卡尔曼滤波算法对电机系统参数进行在线估计，得到转子的位置，以便缩短电机的响应时间。该算法已经考虑了系统参数误差和干扰，所以这种算法对系统外部干扰有强适应性。为了表述整个过程，可以由下式表示：

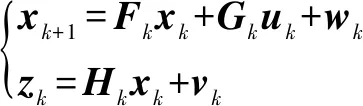
(7)

其中:、、为相关系数矩阵;表示过程噪声;表示测量噪声。它们都是不相关的零均值高斯白噪声，它们的协方差矩阵是和。

卡尔曼滤波算法的一个周期有2个主要阶段：预测和更新。预测步骤使用来自前一时间步的状态估计来产生当前时间步的估计，这种预测状态估计也称为先验状态估计。在更新阶段，当前先验预测与当前观测相结合，用于将状态估计细化为后验状态估计。其中，预测阶段为预测状态及其协方差估计的计算：

(8)

更新阶段为测量误差及其协方差的计算：

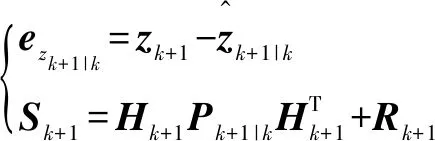
(9)

然后，最佳卡尔曼增益的计算：

(10)

最后，更新状态及其协方差估计的计算：

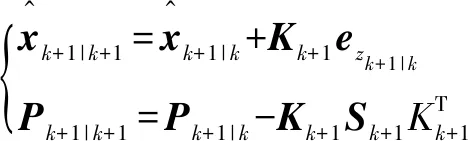
(11)

卡尔曼滤波算法是一种有效的高斯过程最优滤波算法。当对象模型足够精确时，性能更好；但当模型存在误差时，这种增长记忆滤波器使得“旧的”测量数据对当前状态会产生发散的影响。

2.4 鲁棒H∞控制器的设计

在设计鲁棒H控制器的阶段，需要一个面向控制的模型，该控制策略的主要目标是在不影响弓网接触力平均值的情况下减少接触力的波动。通过将参考值作为干扰可以将其视为跟踪问题。因此，可以通过最小化实时接触力与参考值之间的差异来实现控制目标：

min[()]=min[-()]

(12)

其中:()为跟踪误差;为参考值;()为实时接触力。

给定正标量和，使得存在适当维数矩阵的正定对称矩阵>0和普通矩阵,并且满足以下矩阵关系：

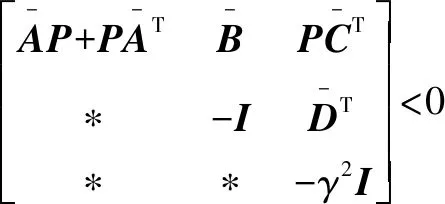
(13)

(14)

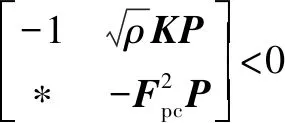
(15)

=

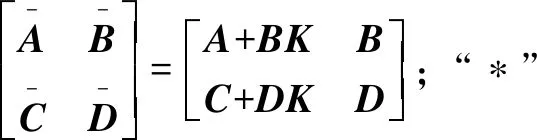
(16)

结合主动控制模型，受电弓主动控制力可以表示为

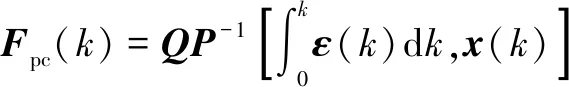
(17)

3 仿真实验分析

3.1 电机系统参数的设置

对于永磁直流电机，系统参数设置如下：扭矩常数=25.1 mN·m/A，速度常数=380 r/(min·V)，每相电阻=0.454 Ω，转动惯量=135 g·cm，每相的电感=0.322 mH,阻尼系数=0.000 2 N·m·s/rad,极对数=2,电源为直流220 V。

H控制器的有效性和鲁棒性通过一个线性控制模型可以得到验证。控制增益矩阵参数计算如下：

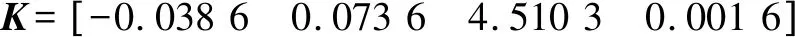
3.2 实验仿真结果分析

根据弓网模型的参数和电机系统参数，进行了Simulink仿真实验，对控制策略进行了评估，如图5所示。

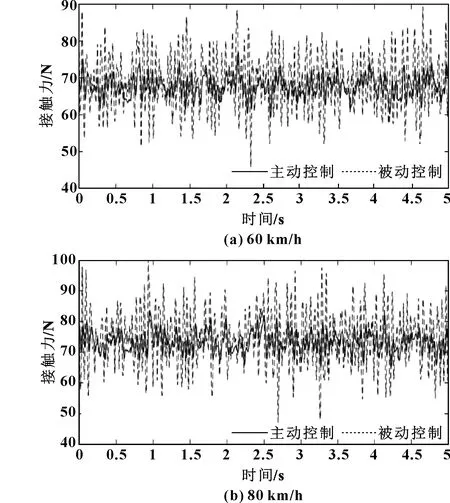
图5 不同时速下的接触力响应曲线

由表2可知：在弓网耦合系统中加入了鲁棒H控制器主动控制策略，在60和80 km/h的速度下，最大接触力的值分别下降了16%和15%，最小接触力的值分别上升了50%和44%；在60和80 km/h的速度下，标准差分别降低了9%和8%。但是在80 km/h的速度下，控制的效果没有那么明显，原因是电机的响应速度一定,单轨列车随着速度的增加，对高频的信号愈发敏感。

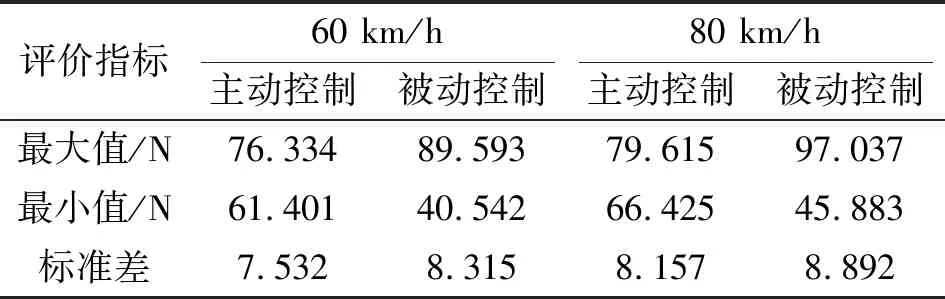
表2 不同时速下弓网受流质量评价指标统计

如图6所示是80 km/h时速下质量块和位移曲线。

图6 80 km/h时速下位移曲线

图7所示是实测重庆市轨道三号线双龙至碧津在80 km/h时速下，受电弓弓头的频率响应曲线。可知：弓头振动的频率集中在0～25 Hz以内，并且主要频率成分小于13 Hz左右，这能反映出弓网系统的低频振动特性，同时电机主动控制的反应速度也符合这频段所产生的激励。

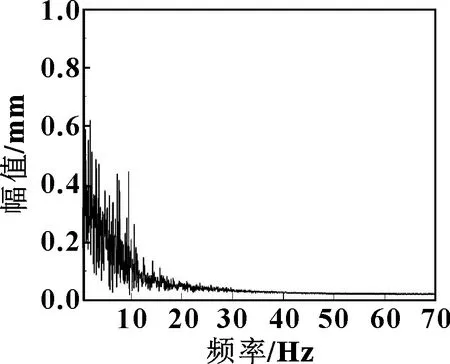
图7 80 km/h时速下弓头频特曲线

4 结论

本文作者提出了一种基于鲁棒H控制器的受电弓主动控制策略，用于减小弓网接触力的波动。首先借鉴了高速铁路的主动控制方法，建立了一种二自由度的主动控制模型，以直流电机作为执行机构进行弓网接触力的调节；然后根据直流电机的相电流和相电压等信号，利用卡尔曼滤波算法对电机转子位置进行估计；最后在鲁棒H控制器的作用下，弓网系统的接触力得到了有效的控制。

研究结果表明：该控制策略有效降低了弓网接触力的波动，减小了标准差。在60和80 km/h的速度下，分别降低了9%和8%。总体来说，该控制策略相比现有的控制策略突出的地方在于：采用了卡尔曼滤波算法对电机转子位置进行了估计，对电机给出了一种更有效的估计方法。最后，所有的这些结论都通过大量的实验进行仿真，进一步验证了所设计的主动控制策略的有效性和鲁棒性。