激励因素对人字齿行星齿轮系统动态特性的影响

林何，李瑞华，孟渔航

(1.西安工程大学机电工程学院，陕西西安 710084；2.西安工程大学，西安市现代智能纺织装备重点实验室，陕西西安 710600)

0 前言

人字齿行星齿轮作为大功率、高转速传动形式的一种，被广泛应用于风电、航空航天、船舶重工等工业传动领域。随着人字齿行星齿轮应用范围的扩展和性能需求的提高，影响系统振动不均的因素越来越受到重视。为了改善人字齿行星齿轮传动系统的动载稳定性，国内外学者不断提出新的方法或技术对人字齿行星齿轮传动的动态特性进行研究。WEI等提出了一种利用虚拟等效轴单元的动力学建模方法，构建了人字齿行星齿轮系统的动力学模型。MO等基于集中参数理论和Lagrange方法建立了人字齿行星传动系统的动力学模型。李同杰等建立了直齿行星齿轮传动纯扭转动力学模型，分析了激励频率、齿侧间隙对该系统动力学特性的影响。但行星齿轮系在啮合传动过程中各齿轮的动载特性还会受到阻尼、综合啮合误差和时变啮合刚度等因素的影响。WANG和WU以风电减速箱行星齿轮传动系统的纯扭转非线性动力学模型为研究对象，对比并分析了不同阻尼比对该系统动力学特性的影响，但是没有涉及其他激励因素对振动的影响。国内研究人员还分析了啮合相位对行星齿轮传动系统动力学特性的影响，发现啮合相位差越小行星齿轮系统的平移振动越小。这些研究主要集中于单个因素对系统动态特性的分析。人字齿齿轮在结构上可视为2对斜齿齿轮的组合体，独特的结构特性使其在啮合过程中同时存在多点啮合和多源激励的情形，轮齿不断的接触和脱离过程中不断地承受冲击降低了运动稳定性，对其动载特性的研究对于系统的整体稳定尤为必要。

为进一步探究激励因素对系统在啮合过程中动态特性的综合影响。本文作者建立人字齿行星轮系的纯扭转非线性动力学模型，使用Runge-Kutta法进行数值求解，分析激励因素对内、外啮合副动载性能的影响规律，并借助三维速度-频率扫描瀑布图、相图和Poincaré映射研究系统的动态特性，对系统倍周期响应进行分析。

1 动力学模型与求解

人字齿行星齿轮系传动系统简图如图1所示。行星齿轮系主要包括一个太阳齿轮(s)、多个相同的行星齿轮(p)和一个内齿圈(r)，行星齿轮主要由一个行星架(c)通过中间的滚动轴承进行刚性连接。输入扭矩作用在太阳轮上，输出扭矩作用在行星架输出轴上。图2中-为系统全局坐标系。动力学模型中单个人字齿轮分为左斜齿轮和右斜齿轮，2个斜齿轮之间视为欧拉梁单元衔接。

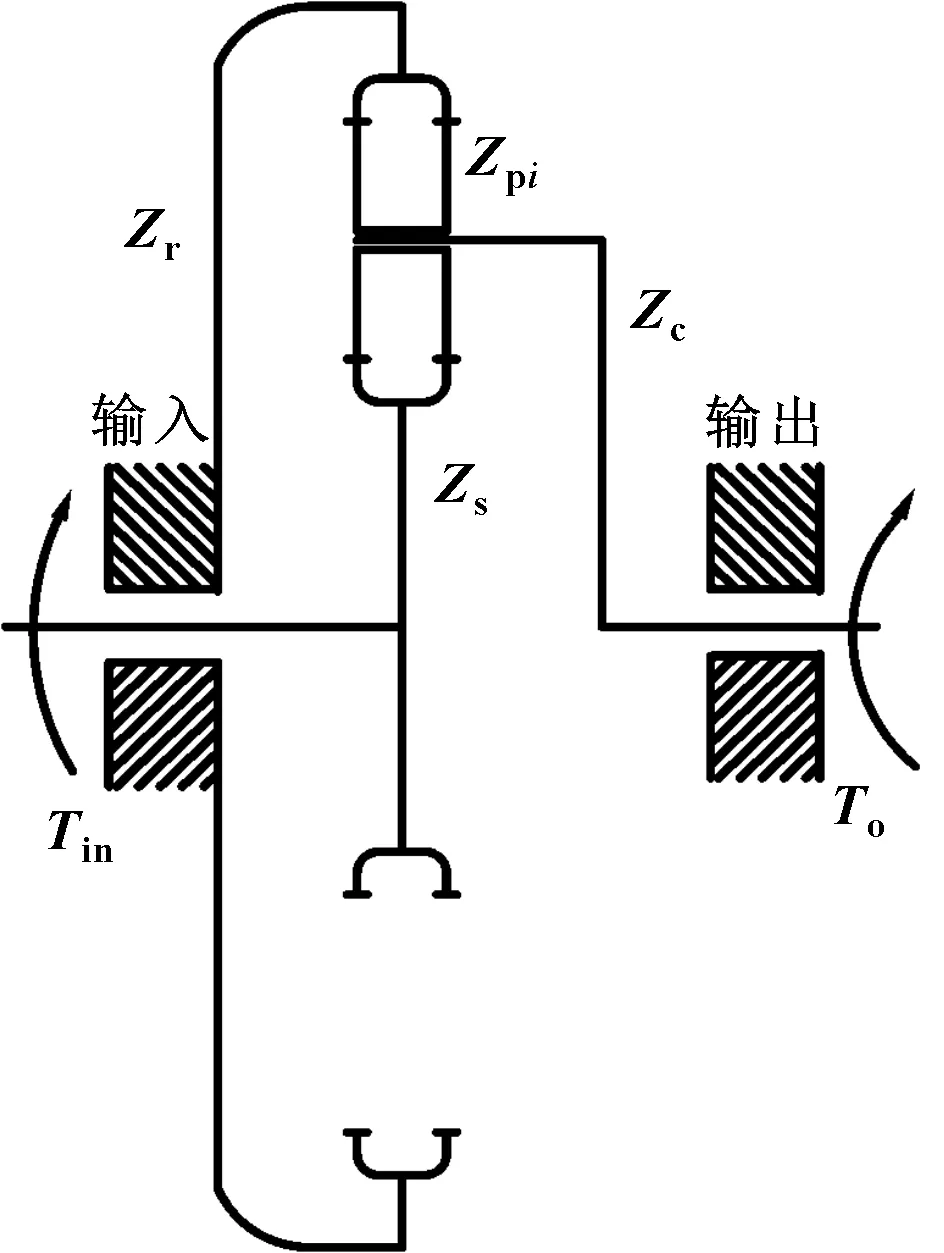
图1 人字齿行星齿轮系传动系统简图

图2 人字齿行星齿轮系的纯扭转非线性动力学模型

所建动力学模型中作出如下假设：(1)模型中各个转动体均关于其扭转中心对称，各齿轮视为刚体且物理属性相同。(2)斜齿轮由于接触的齿对数量波动而导致的啮合刚度的时变分量被忽略。(3)轮齿滑动产生的摩擦力忽略不计。(4)啮合线位于啮合平面内，阻尼力和啮合力视为啮合位移函数。不考虑内齿圈的扭转振动，采用集中质量法建立含间隙人字齿行星齿轮动力学方程组(式(1))：

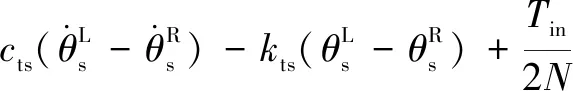
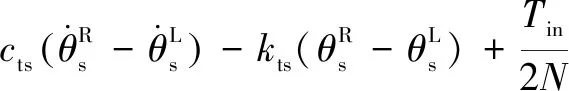
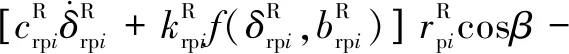
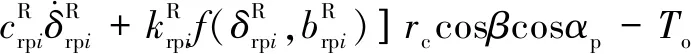
(1)

内齿圈固定，认为内齿圈不产生振动，微分方程数量减1。

(sp,sp)是非线性间隙函数，具有分段线性特征。为等效实际啮合传动，令齿侧间隙为2，有:

(2)

取= 10 μm。

方程组后续需进行消除刚体位移及量纲一化求解，需将角位移转变为相应基圆切线上的等价线位移。即

(3)

(4)

动力学模型中，太阳轮、行星轮和内齿圈可视为两个斜齿轮通过梁连接，则太阳轮、行星轮和内齿圈在扭转方向存在刚体位移，使得方程组(1)成为奇异方程组，解不收敛。故引入转动刚体间的相对位移、p，即

(5)

将式(5)代入式(1)，再将方程组(1)代入式(3)和式(4)中消除刚体位移，消去刚体矩阵奇异性，构建新方程组。

在数值计算中，若同一方程中的系数量级相差很大，计算时容易出现病态问题，因此需要对方程组进行量纲一化处理。

定义各构件的等效质量为:=，系统固有频率为

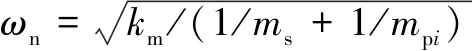
(6)

(7)

将未经量纲一化处理的参数代入消刚体位移后的方程组中，进行量纲一化处理，得到不含刚体位移的含有16个自由度的间隙型非线性方程组，整理后统一形式为

(8)

式中:为量纲一化后的啮合位移;、、和4个系数矩阵分别为量纲一化后的质量矩阵、阻尼矩阵、刚度矩阵和载荷矢量。其中=[,p,sp,rp]，=1,2,3，=1,2，1为左侧，2为右侧。需要说明的是因系统整体动力学方程复杂，参数较多，故只将内、外啮合位移sp、rp的阻尼矩阵与刚度矩阵列出，即：

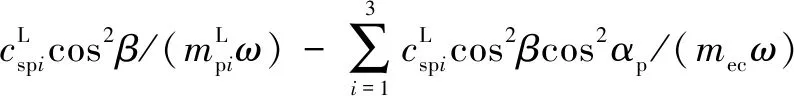
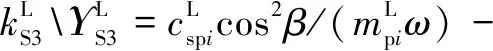
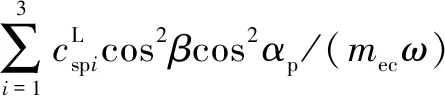
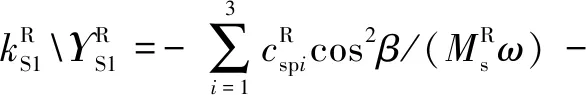
coscos()

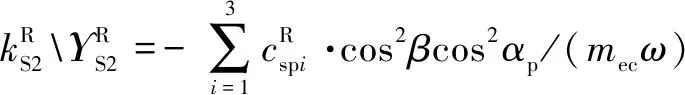
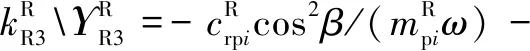
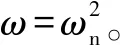
利用Fourier级数展开式表达时变啮合刚度，则时变啮合刚度表达式为

(9)

式中:(sprp)为内、外啮合副时变啮合刚度均值;为刚度波动系数;为啮合频率;为初相位;=1,2,3。

阻尼根据时变啮合刚度进行确定，其表达式为

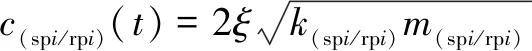
(10)

式中:为阻尼比;(sprp)为内、外啮合副的等效质量;=1,2,3。

综合啮合误差一般采用简谐函数描述，即

(sprp)()=(sprp)sin(+(sprp))

(11)

式中:(sp/rp)为各啮合副综合啮合误差幅值;(sp/rp)为各啮合副综合啮合误差初相位；=1,2,3。最后对量纲一化后的微分方程组使用Runge-Kutta法进行求解。

2 振动特性

动力学系统中的行星轮数目=3；齿轮两侧斜齿轮的螺旋角=16°，法面压力角=20°；输入转矩=891 N·m；外啮合的啮合刚度=8.38×10N/m，内啮合的啮合刚度=7.62×10N/m；动力学系统中其余主要物理参数如表1所示，为简化系统分析计算，人字齿轮左右斜齿轮参数均视为相同。以下所有非线性参数分析均以人字齿左侧齿轮为主。

表1 人字齿行星齿轮系统主要动力学参数

2.1 阻尼变化激励

图3、图4所示为外、内啮合的动载特性随阻尼的变化曲线。给定4种转速考察系统的动载特性，转速对应的量纲一啮合频率为1.5、1.7、1.9、2.1，阻尼比取值区间为∈[0.015,0.05]。图3中:当为1.7时，动载系数在∈[0.021,0.023]区间内突降到1.789,然后激增到1.84；然后随着阻尼比数值增大动载系数持续增长，在=0.038时从1.859降低到1.842左右后缓慢降低；动载系数在∈[0.021,0.023]内和=0.038时均出现短时剧烈波动，可能是外啮合在此区域内产生非线性混沌振动，使得载荷情况突变。内啮合(图4)的动载系数变化趋势与外啮合相似但变化范围总体降低，说明行星齿轮系统在重载工况下稳定性更好。其激增原因与外啮合激增类似。整体上来看，随着与增加，系统的稳定趋势明显。

图3 外啮合的动载特性随阻尼的变化 4 内啮合的动载特性随阻尼的变化

2.2 时变啮合刚度激励

图5、图6所示为外、内啮合的动载特性随时变啮合刚度的变化曲线。选定刚度波动系数∈[0.1,0.35]，量纲一啮合频率取1.7、1.9、2.1。图5中，当为1.7时，在>0.17时，动载系数产生波动；在刚度波动系数=0.22时，动载系数急剧增加到1.87，发生失稳现象，使得系统啮合传动状况急剧变化，然后动载系数下降至1.8左右，随后动载系数虽有波动，但总体处于下降趋势；当为2.1时，动载系数则在>0.2时在1.84上下发生波动。如图6所示：内啮合动载系数的波动相较于外啮合动载系数的变化更加平缓。整体上看，随着刚度波动系数的增大，系统的动载特性会逐渐失稳，但随着齿轮转换为纯刚性件，系统的承载能力和传动效率将得到提高。

图5 外啮合的动载特性随时变啮合刚度的变化 图6 内啮合的动载特性随时变啮合刚度的变化

2.3 综合啮合误差激励

图7、图8分别为外、内啮合的动载系数变化。当=1.7，综合啮合误差∈[0.2,0.3]时，内、外啮合的动载系数均出现突变，其产生剧烈波动的原因推测是在此区间中出现了微弱的齿背冲击，使得动载波动；当>0.33时动载系数发生剧烈变化，出现了非线性混沌振动，使得系统的啮合传动强烈振动。在相同的系数范围内，内啮合的动载系数变化趋势与外啮合基本一致，但内啮合动载系数变化幅度较外啮合有所减弱，行星齿轮均载能力得到验证。总体来看，随着综合啮合误差的增加，内、外啮合的动载系数的变化主要呈递增趋势，则说明在此系统中，综合啮合误差应越小越好。

图7 外啮合的动载特性随综合啮合误差的变化 图8 内啮合的动载特性随综合啮合误差的变化

2.4 非线性特性

在上述动载性能的分析中，=0.22、=0.22、=0.4时动载系数的突变程度最大。将以上3个突出值输入系统，然后对外啮合不同输入速度下的稳态响应进行傅里叶变换，获得不同转速下单独的频率内容，最后得到如图9所示速度-频率扫描图的系统整体振动的三维瀑布图。瀑布图中每个转速下的振动含有多个离散独立分布的频率。这种模拟形式可将振动情况水平分成几个网格谐波，一次谐波比其他高次谐波更多地支配振动频谱，特别是在运行速度较高时。此外，一次谐波和二次谐波的最高峰均对应同一频率即1 671 Hz，该频率为系统固有频率的1/3，出现在激振频率之后，系统出现超谐波共振，因此在系统运行中应注意共振情况。在两次谐波之外，还存在一些谐、杂波，这些谐、杂波对于系统的运转会产生一定冲击，但是影响范围有限。

图9 891 N·m输入扭矩下量纲一位移和动态啮合力响应的速度扫描瀑布图

图10 外啮合量纲一位移-速度相图和Poincaré映射

为进一步分析系统动态特性，将一次谐波中的最大波峰对应的太阳轮转速5 013 r/min设定为系统输入转速,得到如图10所示的外啮合量纲一位移-速度相图和Poincaré映射图。图10中相轨迹在不重合的前提下呈现交叉和缠绕现象最终形成闭环，吸引子充满整个超环面，运动过程中并未出现明显的齿背冲击；吸引子点集呈现一定的拟双周期振动特征，与图9(a)三维瀑布图中有2次谐波和一些谐、杂波的频率信息相吻合，表明系统此时处于拟二倍周期运动状态，但是存在一定的干扰。结合瀑布图、相图和Poincaré映射，说明系统在给定值区间仍然处于收敛状态。

3 结论

(1)内、外啮合的动载系数变化趋势大致相同情况下，r-p啮合副的波动总要低于s-p啮合副，内啮合具有更好的振动稳定性。

(2)阻尼比变化下的动载系数总体呈减小趋势，但在∈[0.021,0.023]区间内动载系数发生突减现象；动载系数随着刚度波动系数和综合啮合误差数值增大而发生失稳现象，产生激烈波动，因此在系统中要避免两者数值过大使得系统失稳。

(3)系统发生了超谐波共振，在最高振幅对应的转速时系统处于拟二倍周期运动，系统在给定区间内收敛不发散。实际工况中应尽可能地使系统处于合适的激励频率区间，避开大范围混沌运动以减轻系统的振动。