例析板块模型题的多种解法

贾天东

(甘肃省临泽县第一中学)

板块模型问题是高中物理中的常见问题,且多为综合类计算题,对大多数学生来说有一定难度,在学习过程中,如果对所学知识理解不够深入,又不能灵活应用,一旦遇到创新型题型,则很容易出现错误.其实,物理学习重在掌握原理,只要抓住问题的本质(涉及的物理原理)就可以轻松解题.本文通过对一道板块模型的典型例题进行一题多解分析,以期实现对这一题型的掌握.

例如图1 所示,光滑水平面上放着一个长木板,在木板右端静止放着一小木块.已知长木板的长度L＝1.6 m,质量M＝3.0kg;小木块的质量m＝1.0kg;长木板和小木块之间的动摩擦因数μ＝0.1;木板受到向右的水平拉力F＝10N,为了使长木板能从小木块的下方抽出,水平拉力F的作用时间至少应为多少? (g取10m·s－2)

图1

解析方法1利用运动学公式和牛顿第二定律解题.

设水平拉力F作用的最少时间为t1.在撤去水平拉力后,当小木块运动到长木板的最左端时,小木块和木板的速度刚好相同,设为v;该过程小木块运动的时间为t2.另设在时间t1内,小木块向右做匀加速直线运动的末速度为v1,加速度为a1,位移为s1;长木板向右做匀加速直线运动的加速度为a2,末速度为v2,位移为s2.

根据牛顿第二定律,对小木块有

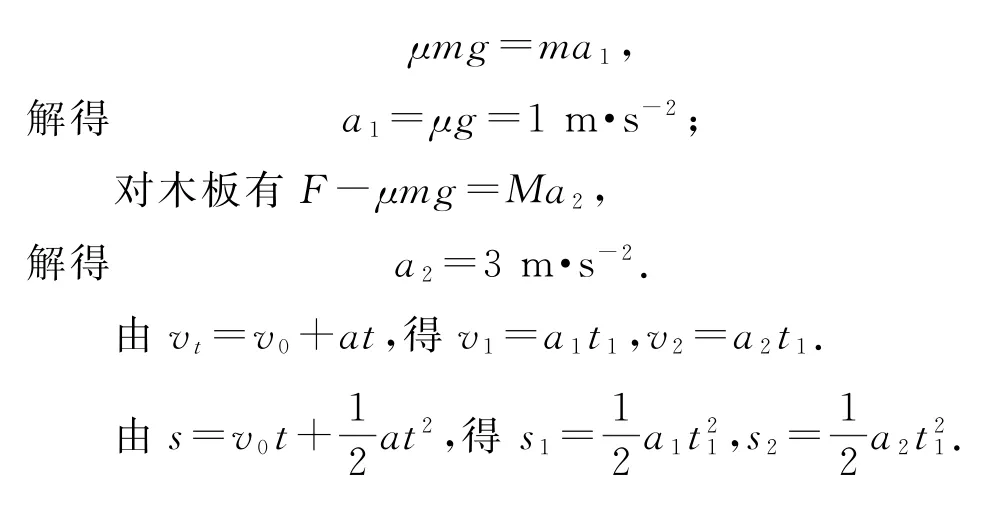
此过程中,小木块在长木板上滑行,二者相对位移Δs1＝s2－s1.

撤去水平拉力F后,小木块运动到长木板的最左端时,二者刚好有相同速度v,此过程,小木块向右做匀加速直线运动,设其加速度大小为a3,运动位移为s3;木板向右做匀减速直线运动,设加速度大小为a4,运动位移为s4.

对小木块有μmg＝ma3,解得

由题意可知L＝Δs1＋Δs2,解得t1＝0.8s.

方法2利用动量守恒定律、动量定理、动能定理和功能关系解题.

设水平拉力F作用的最少时间为t1,在其作用的时间t1内,小木块的末速度为v1,运动的位移为s1;木板的末速度为v2,运动的位移为s2.

有水平拉力F作用的运动过程中,根据动能定理,对小木块有

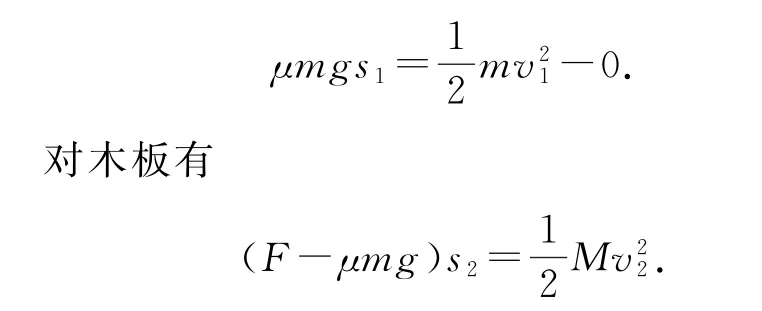
规定向右为正方向,整个运动过程根据动量定理,对小木块有

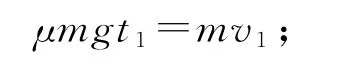
对木板有

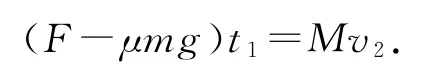
有水平拉力F作用的运动过程中,小木块在长木板上滑行,其滑行的位移为Δs1＝s2－s1.

撤去水平拉力F后,设小木块运动到长木板的最左端时,二者恰好达到相同速度v.因为在这个运动过程中,小木块和长木板组成的系统所受的合力为零,所以动量守恒.由动量守恒定律得

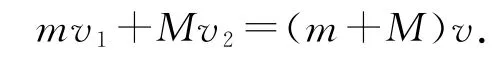
设撤去水平拉力F后,小木块在长木板上滑行的位移为Δs2,由功能关系可得

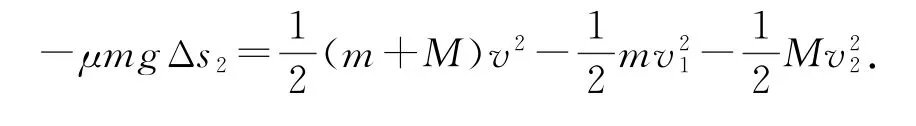
由题意可知L＝Δs1＋Δs2.

综合以上各式,代入数据可解得t1＝0.8s.

方法3利用功能关系和动量定理解题.

设水平拉力F作用的最少时间为t1,在有水平拉力作用时,长木板向右做匀加速直线运动的加速度为a,位移为s;撤去水平拉力F后,设小木块运动到长木板的最左端时,二者恰好达到相同速度v.

在有水平拉力F作用的运动过程中,由牛顿第二定律,对木板有

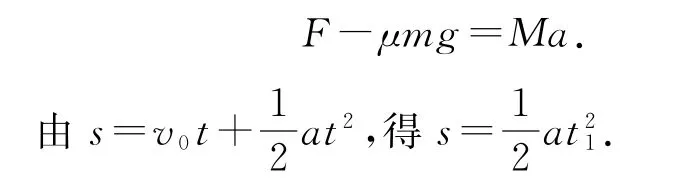
对小木块和长木板组成的系统,整个运动过程中,由动量定理得

对小木块和长木板组成的系统,整个运动过程中,由功能关系得

综合以上各式,代入数据可解得

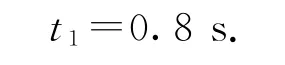
方法4结合图像解题.

设水平拉力F作用的最少时间为t1,撤去水平拉力F后,设小木块运动到长木板的最左端时,二者恰好达到相同速度v;设从撤去水平拉力到小木块和长木板速度相等,二者运动的时间为t2.

在有水平拉力F作用的运动过程中,设小木块向右做匀加速直线运动的末速度为v1,加速度为a1;木板向右做匀加速直线运动的末速度为v2,加速度为a2.

根据牛顿第二定律,对小木块有

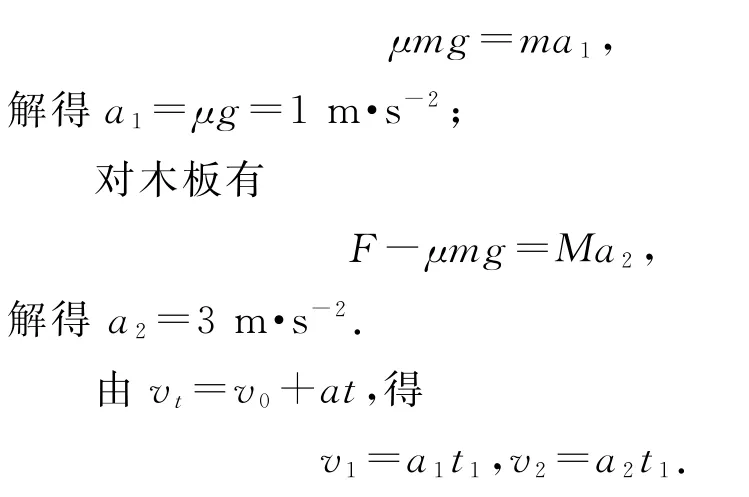
撤去水平拉力F后,设小木块运动到长木板的最左端时二者恰好达到相同速度v,因为这个过程中,它们组成的系统所受的合力为零,系统动量守恒,故由动量守恒定律得

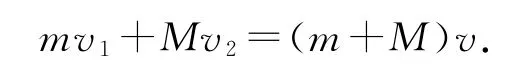
规定向右为正方向,对撤去水平拉力F后的运动过程分析,对小木块和长木板分别由动量定理得

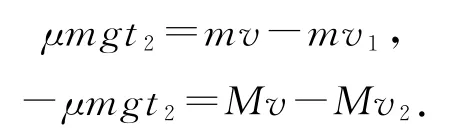
如图2所示,分别画出小木块和木板的速度随时间变化的图像,其中,表示长木板的“速度—时间”图像是OAB,表示小木块的“速度—时间”图像是OB.根据图像的物理意义可知,“v-t图像与横轴所围图形的面积表示物体运动的位移”,即△OBD的面积表示小木块全过程的位移,四边形OABD的面积表示长木板全过程的位移,而△OAB的面积表示全过程中小木块在长木板上滑行的位移,即

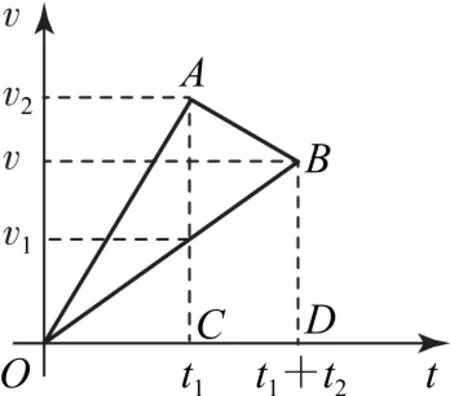
图2

综合以上各式,代入数据可解得t1＝0.8s.

以上通过4种解法对板块模型进行了简单总结和分析.通过比较,不难看出各种解法的特点.本例题有一个隐含条件——撤去水平拉力F后,小木块运动到长木板的最左端时,二者刚好达到相同速度.不论哪种解法,挖掘这个条件都是无法绕过去的解题关键,可见,解法其实都是辅助解题的工具,不论试题如何变形,其涉及的物理规律永远不会变化,因此,只要抓住解题关键,便可挑选自己最熟悉的方法进行解题.

(完)