基于动能定理的发电系统机械转动惯量研究*

白望望，杨振斌，杨德州，张中丹，冯智慧

(1.国网甘肃省电力公司经济技术研究院，甘肃 兰州 730050; 2.兰州理工大学，甘肃 兰州 730050)

0 引 言

电网惯量这一概念源自发电机机械转动惯量，用以衡量电力系统抵抗频率突变的能力，电力系统的惯量即为系统阻抗自身能量波动的固有属性，通常由并网同步发电机的转子、轴系、齿轮等存储的动能提供。新能源电力系统惯量作为防止频率变化的第一道防线，成为评价系统安全稳定性能的重要指标[1]。新能源发电系统通常运行在最大功率跟踪模式，利用电力电子器件接入电网，其源侧和网侧天然解耦，一个地区的惯量无法及时响应另一个区域的频率波动，导致系统惯量减少、频率响应能力降低[2]。新能源电力系统中存在严重的惯量不足及频率稳定性问题，这给电力系统的正常运行带来严峻的隐患，因此，如何准确评估电力系统的惯量十分重要。

针对新能源电力系统惯量水平低下和频率稳定性下降的问题，国内外学者展开了大量的研究。文献[3]为量化系统频率响应能力，在分析系统惯量需求必要性前提下，提出考虑频率变化率及最低点频率约束的系统所需最小惯量的评估方法。文献[4]通过切机后同步相量测量单元(phasor measurement units,PMU)采集的各个区域瞬时频率变化来估计系统惯量水平，同时考虑了负荷侧及新能源虚拟惯量控制对系统惯量的贡献。文献[5]考虑频率的分布特性，采用惯量图心作为频率采集点并评估系统惯量水平，该方法降低了评估过程中对测量数据点的需求。文献[6]对电力系统的节点惯量不仅进行了物理说明，而且还研究其表征方法，通过基于扰动故障下节点频率的动态特性，实现对电力系统惯性的实时监控。文献[7]将电网中频率与系统采集的惯性时间常数历史数据相结合，根据两者之间变化的相关性，建立统计模型。由统计模型估计出系统的惯量水平。因此，如何合理评估系统的惯量水平，对于提高新能源的消纳和电力系统的频率稳定性意义重大。

综上所述，由于传统电力系统发电机与电网直接连接，当系统出现功率缺额或盈余，发电机旋转质块通过释放或吸收动能，响应由系统功率波动引起的电磁功率与机械功率偏差，支撑系统功率并抑制频率变化。而新能源接入后，不具备响应扰动功率的能力。因此，基于动能定理，研究发电系统机械转动惯量，已达到获取系统实时惯量的目的，对发电系统的启停具有指导作用。建立了PSASP电网模型，验证了方法的有效性，为新能源发电系统频率稳定性分析提供建议和参考。

1 发电机区域划分与选择

在系统出现功率不平衡时，机组的输出电磁转矩迅速增加，导致机械转矩低于电磁转矩，此时转子减速，释放自身存储动能，此为惯性响应，随着大规模新能源机组的并网，以及常规电源持续减少，使系统原本充足的惯量变得薄弱，各地区惯量水平分布不均匀的特点越来越突出，电力系统频率响应呈现出明显的时空分布特性，不同区域惯量分布会对系统的频率响应造成较大影响[8]。因此，首先根据频率响应特性对系统进行区域划分，通过分析各区域机组抗扰程度的强弱，确定区域核心机组，通过区域核心机组的选择，可以降低惯量评估中对测量数据的需求。

1.1 发电机节点电气距离

当电网内某个节点的变量发生变化时，其附近区域节点的运行状态也随之改变，这种关系称为节点间的耦合性。在电力系统中，通常采用“电气距离”来表示任意两节点之间的电气耦合程度，其值越小，耦合性越强[9]。

通过电气距离对系统中发电机节点进行分区，将电气距离相近的机组划分为同一区域。发电机节点之间的电气距离可通过系统导纳矩阵分析得出，通过对收缩到发电机内电势节点的系统导纳矩阵进行分析，并进行各机组的分区。这里的导纳矩阵处理参照文献[10]所述，为了直观了解不同发电机之间的关联程度，对系统导纳矩阵进行归一化处理：①获取收缩到发电机内电势节点的系统导纳矩阵Y；②进行归一化处理，得到表示电气距离的相关度矩阵Z。

电气距离相近的机组对应的相关度矩阵中元素趋于相似，可以将其划分到一个区域，而电气距离相距较远的机组对应的相关度矩阵中元素相差较大，可以将其划分到不同的区域。

1.2 基于聚类原理的系统区域划分

聚类是一种典型的无监督学习方式，依据某个特定准则，将所得的数据组合划分成不同的类或簇，使得所划分的区域数据对象的相似程度尽可能大[11]。因此，将聚类分析用于系统的区域划分，聚类分析的目标就是在相似的基础上收集数据进行分类，分析结果使得相同类别数据之间尽可能相似，不同类之间有明显区别，对相关度矩阵Z进行聚类分析，实现系统中各发电机的分区。

1.3 区域核心发电机组的选择

对系统进行区域划分后，同一区域内机组相似程度较高，通过选择各区域核心机组来避免评估过程测量数据需求多且容易引起误差的问题，核心机组的选择标准能够表征该区域的频率信息，可以将其作为评估过程所需的数据采集点。从影响程度的强弱来看，核心机组的选取主要考虑发电机节点之间的电气距离、发电机机组惯性时间常数H，代表整个系统中适合的频率采集点，为此提出了一个核心机组选取的指标概念，发电机的影响因子FA，其公式如下：

(1)

式中：Hu、du分别为发电机u的惯性时间常数与发电机节点间的电气距离；nG为系统中发电机的个数；du为发电机节点间的电气距离，采取归一化处理后其相关度矩阵用Z来表示。

2 电力系统机械转动惯量评估

2.1 基于动能定理的惯量评估方法

新能源接口取代了传统的机械开关并网，为了能够对新能源接入电力系统惯量水平有一个基本的认识，需要对新能源电力系统进行惯量评估。相比较而言，基于动能定理的惯量评估方法不需要计算系统的频率变化率，降低了在计算频率变化率时产生的误差[12]。需要采集的数据包括区域间联络线上功率，区域核心机组频率。在采集数据的选择过程中均取一个时间窗内对应的平均值，其目的是为了避免某个测量点造成的偶然误差。

根据惯性时间常数和惯量的定义，惯性时间常数H可以解释为同步发电机旋转部件中的动能传递给与同步发电机额定功率相等的负载所需要的时间。扰动发生后，系统的惯量响应最先动作。这个过程一般为扰动开始后的2 s内。然后调节系统开始工作，所以在扰动发生后的2 s内，可以根据惯量响应时的能量输送关系，来评估电力系统的惯量水平。

对于单个机组而言，惯量值常用发电机在额定角速度下的转子动能表示，单位为MW.S。表达式如下：

(2)

式中：Ei、Hi、Si、ωn、J分别为发电机i的惯量值、惯性时间常数、容量、转动惯量和额定角速度。

假设系统在t1时刻发生扰动，那么在扰动后的t2时刻，根据公式得到发电机转动惯量的变化量E为：

(3)

式中:J为单台机组转动惯量；ω1、ω2分别为t1、t2时刻的发电机机械角速度。

在扰动发生后的很短时间内，假设同步发电机的转动惯量转化为电功率是一个线性化的过程，由此得到系统有功功率缺额：

(4)

因此，根据动能定理，忽略负荷的频率响应情况，对于单台发电机而言，从采样时刻t1到采样时刻t2所弥补的有功功率缺额为：

(5)

式中：ΔP=Pm-Pe，ΔP是系统有功功率缺额，其中，Pm为系统机械功率，Pe为系统电磁功率。

扰动发生后的2 s左右，惯量响应在系统频率调节中占主要作用[13]。由于系统中的调频系统还未及时响应，区域之间联络线的功率缺额属于系统惯量响应范畴。在此期间由于同步发电机提供的机械功率不能发生突变，因此区域功率偏差可由该区域扰动前、后电磁功率变化量表示，此时联络线功率不平衡是发电机惯量响应的体现。

由以上公式(2)、(5)可知系统的等值惯量Ec：

(6)

根据ω=2πf，公式变换为：

(7)

式中：f2、f1分别为t2、t1时刻的发电机节点处的频率。

从公式也可以得出，系统区域的惯量水平可以通过核心机组节点处的频率与区域间有功功率缺额来计算得到。

2.2 新能源接入点的选择指标

为了表示系统内的惯量分布，将系统中的发电机节点作为处理对象。根据惯量响应理论，当系统发生功率缺额等大扰动时，惯量响应的过程就是阻止系统频率发生变化的过程。因此，如果某发电机节点在发生扰动后，频率的变化较其他节点小时，就可以认为该节点的惯量比其他节点大[14]。反之则该节点的惯量较小。在机组规划时，将对系统表现较高惯量的机组配置在惯量较小节点；而将新能源机组配置在惯量大的节点，在系统拓扑确定时，通过这种方式寻找合理的新能源接入点。

为了定量地表示节点频率偏移量的大小，定义节点对惯量改变的敏感程度为T时间内频率偏移量的绝对值。

(8)

式中：F表示频率总偏移量；r表示某时刻频率偏移量。

2.3 数据处理

为了避免某个测量点造成的偶然误差，在新能源接入点选择和惯量评估的过程中，所需数据的取值均为一个时间窗内对应测量数据的平均值，如图1所示，图中n为每个时间窗内取值个数，Δt为两个测量点之间的时间间隔[15]。

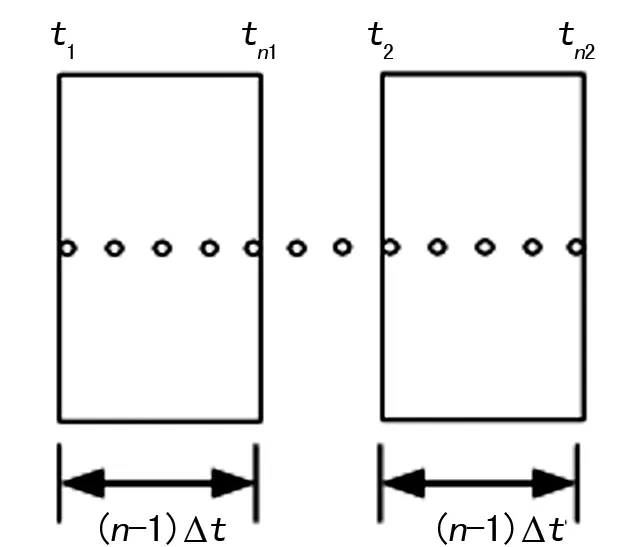
图1 电气量取值时间窗

3 算例分析

以图2所示的EPRI-36节点系统为例，该系统中有8台发电机组，包含多种机组类型。扰动发生后，不同区域机组转子运动存在差异，从而频率响应分布不同，如表1所列为机组的基础数据，主要包括额定有功功率和惯性时间常数，系统联络线分布情况如表2所列。

3.1 【指南建议】 应该遵循用于其他临床诊断测序的实验室质量标准、分析和变异注释原则。与所有的诊断检测一样，该项检测只能在有资质且具有产前基因组诊断检测和解释相关经验的诊断实验室中进行。

图2 8机36节点系统结构图

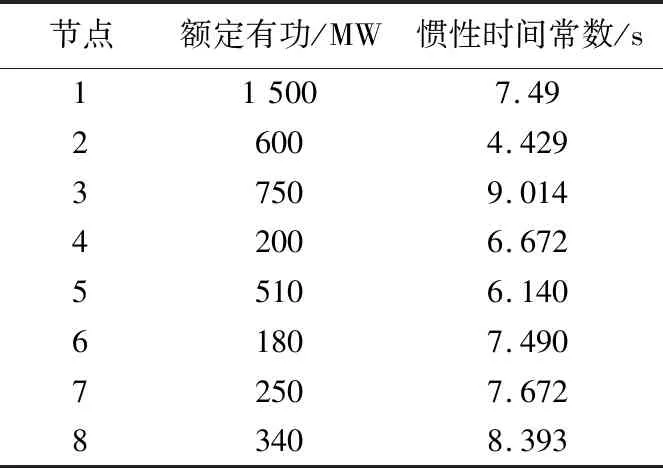
表1 同步机额定有功功率及惯性时间常数

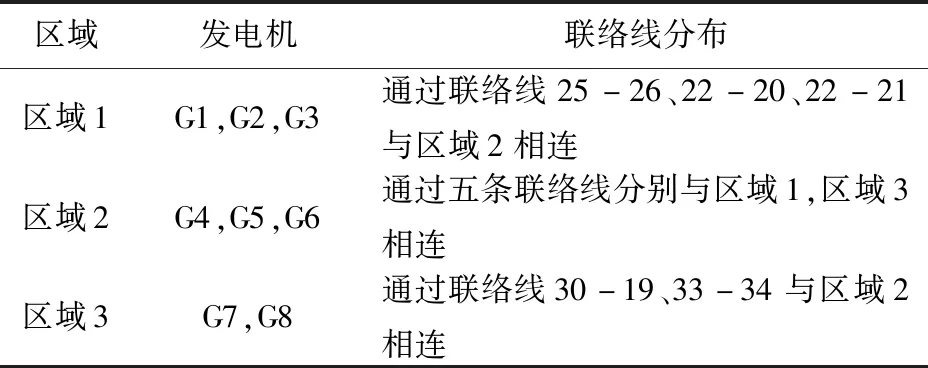
表2 系统联络线分布情况

3.1 系统分区与核心机组确定

文中基于PSASP软件中8机36节点标准数据，根据1.1节和1.2节所述，得到表示电气距离的相关度矩阵Z。采取聚类分析对系统分区，如图3所示。

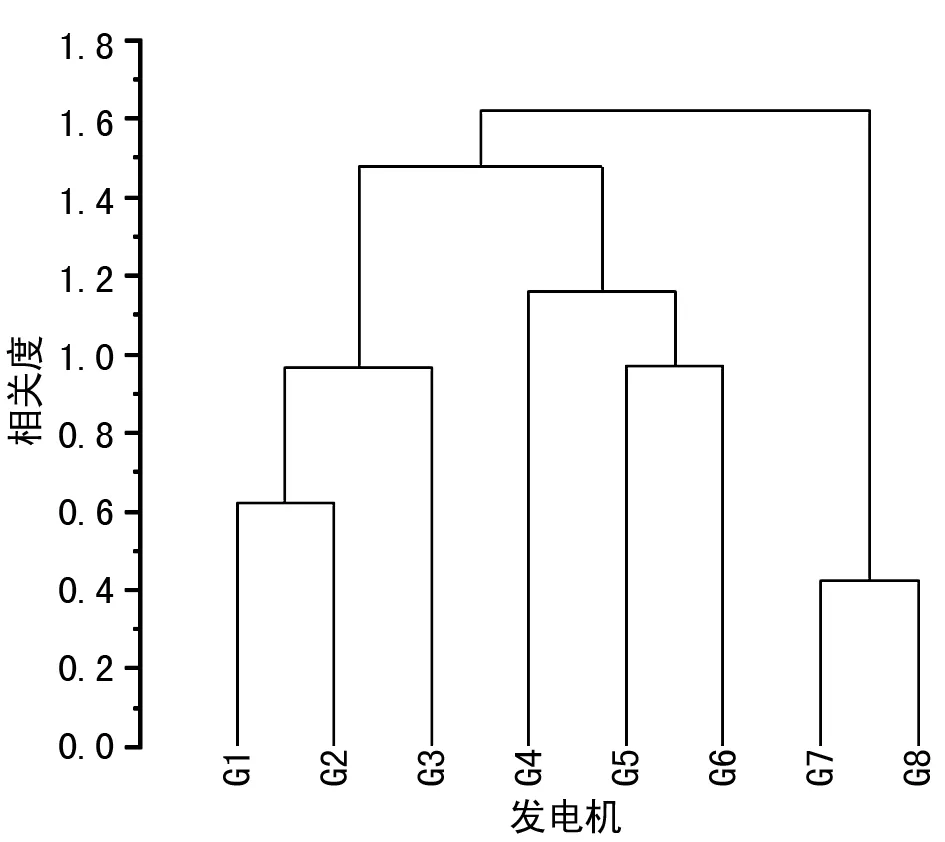
图3 发电机间关联程度

由图3的聚类分析结果可知，1、2、3号机组的相似程度高，可作为一个区域。4、5、6号机组表现出较高的相似性，7、8号机组也表现出较高的相似性。因此，将系统分为3个区域，如表3所列。分区精度越高，则惯量评估精度越高。

表3 系统区域划分情况

根据1.3节所述，区域核心机组的选取主要考虑发电机节点之间的电气距离、发电机机组惯量H，由此可得各区域核心机组的影响因子结果，如表4所列。

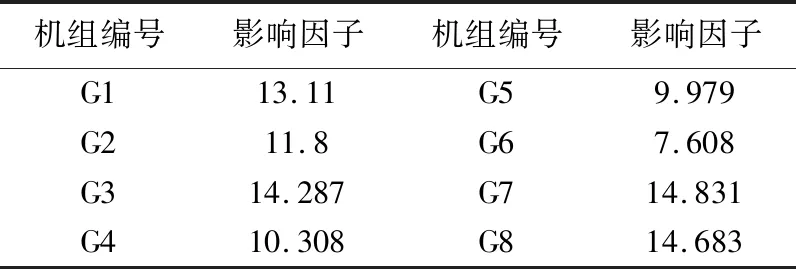
表4 发电机组影响因子

根据上述影响因子的大小，各区域核心机组选择结果如表5所列。

表5 核心机组的选择结果

根据表4、5可知各区域中的核心机组主要为G3，G4，G7。在新能源接入点选取和惯量评估时，由于系统的惯量中心频率难以测量，则可以通过测量核心机组频率予以替换。利用分区和核心机组选择结果，在3个区域联络线上和核心机组G3，G4，G7上分别配置PMU，获取系统的功率和频率数据。

3.2 新能源接入点选择结果

分别在不同发电机节点设置相同的功率扰动，每个节点有功功率的变化应控制在该节点额定有功功率的20%。对系统各核心机组进行切机扰动，以产生功率不平衡量。根据1.4节所提及的计算公式，计算相应时间段节点频率变化的总和。计算数据选取两个时间窗函数对应变化率的平均值，选取故障发生后的两个时间段(2.06～2.1)、(2.16～2.2)，得到发电机频率偏差绝对值之和，确定合理的新能源接入点，分别在以下几种情况进行讨论。

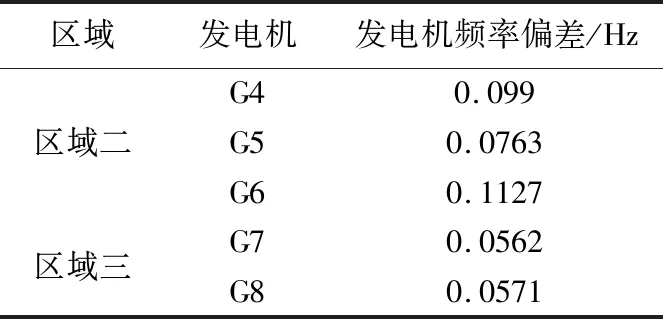
表6 扰动后各区域频率偏差

情况2：选择区域二中的核心机组作为扰动对象，设置扰动为切机20%，测量非扰动区域机组扰动发生后的时间段内频率偏移量绝对值，结果如表7所列。

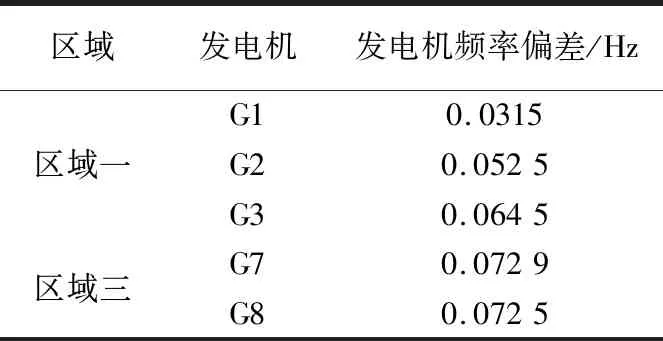
表7 扰动后各区域频率偏差情况2中扰动数据

情况3：选择区域三的核心机组作为扰动对象，设置扰动为切机20%，测量非扰动区域机组扰动发生后的时间段内频率偏移量绝对值，结果如表8所列。

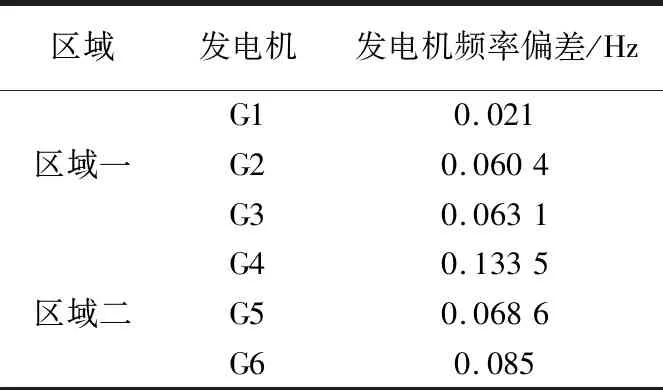
表8 扰动后各区域频率偏差情况3中扰动数据

通过以上分析可得，根据非扰动区域机组频率偏差绝对值之和，可以得到惯量改变对发电机节点影响程度排序，进一步来确定合理的新能源接入点。通过分析可得，频率偏差越小，表明该节点惯量水平较大，在系统渗透率及拓扑结构确定时，更适合新能源接入。

3.3 系统惯量水平的评估

以3.2节中情况1为例，分析各区域最佳新能源接入点。对区域二来说，发电机G5的频率偏差最小，该节点更适合接入新能源机组，则将机组5替换为相同容量的风力发电机。通过对扰动事件的分析，根据动能定理，评估新能源接入条件下系统惯量。设置扰动事件为2 s时系统在发电机4处失去30%的发电量，对扰动后各区域间联络线功率变化和核心机组的频率进行采集，由前面分析可知，惯量响应一般发生在扰动响应后的2 s内，采集t1、t2分别为2.01 s和3.01 s的测量数据。如图4所示。根据动能定理，评估扰动区域和非扰动区域的惯量水平，评估结果如表9所列。

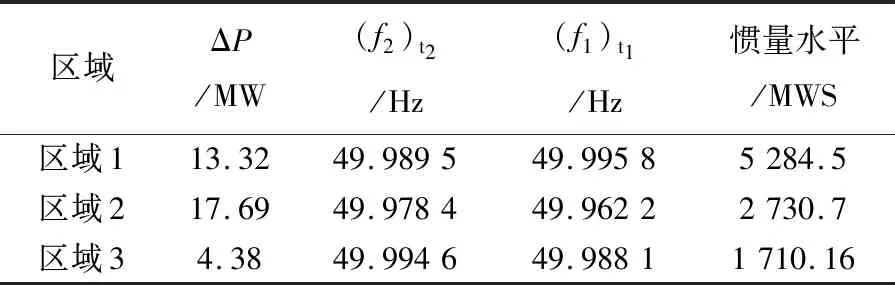
表9 惯量评估结果

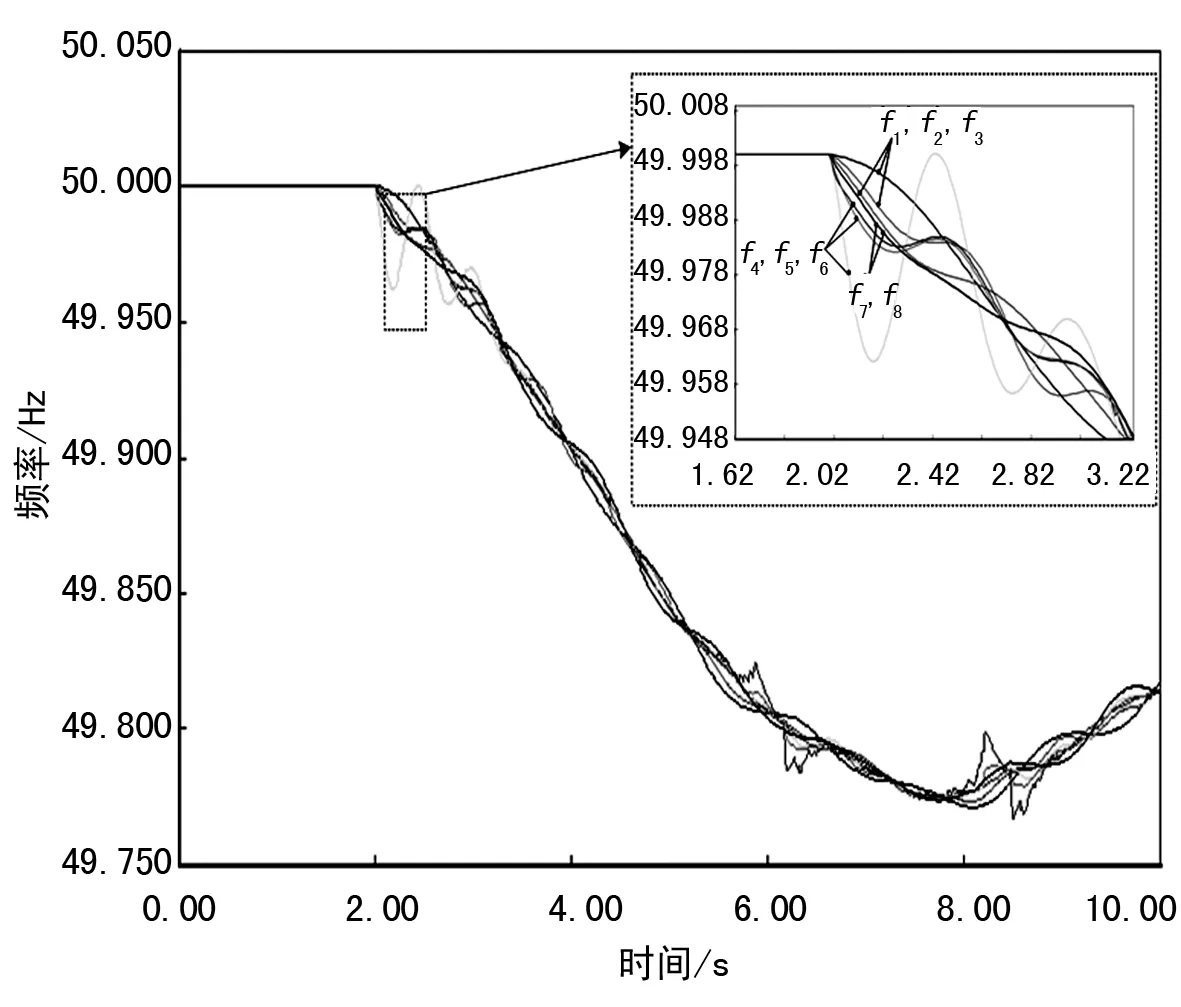
图4 机端频率曲线

利用测量扰动后得到的联络线功率及各区域核心机组频率等电气量，采用动能定理进行分区惯量评估，能较为准确地估计出系统各区域惯量水平。所采用评估方法，能利用较少数据计算得到系统各区域的惯量水平，使系统的惯量评估更简单准确。

4 结 语

由于物理结构的不同，电力电子接口与机械开关接口发电系统在惯量响应特性方面存在很大差异，文中在系统拓扑结构确定的情况下，对系统进行区域划分及确定各区域核心发电机组，进而研究系统惯量的分布强弱。以频率偏差绝对值为指标，寻找最佳的新能源接入点，利用扰动后各区域间联络线功率和核心机组频率的测量值，依据动能定理评估系统区域的惯量水平。降低了测量数据的需求及计算过程的复杂度，在EPRI-36节点系统中设置发电机功率扰动故障，通过仿真验证了所提方法在评估新能源接入发电系统机械转动惯量方面的可行性。