中锰TRIP钢棘轮行为及其本构模拟分析*
彭 磊,张 娟,畅舒心
(西南交通大学 力学与航空航天学院 应用力学与结构安全四川省重点实验室,四川 成都 610031)
0 引 言
作为第三代先进高强钢代表之一,TRIP钢具有高强度和高延伸率,同时其在耐腐蚀性、成本以及抗冲击性能等方面较其它材料具有较大的优势[1-2]。目前以TRIP钢为代表的先进高强钢是汽车工业轻量化设计中的重要材料,在国防工业、铁路交通、船舶航洋等领域也具有广阔的应用前景[3-4]。
棘轮效应是在非对称应力控制循环加载下二次变形的累积。棘轮效应的累积可能导致疲劳寿命的减少或使结构的变形超过限制而不能正常工作,是实际工程结构设计中需要考虑的一个重要问题。为了探究材料在非对称应力作用下的棘轮效应,学者们对大量的金属材料(U75V轨钢[5]、ZK60镁合金[6]、HE1车轮钢[7]和SS304不锈钢[8]等)开展了一系列棘轮行为的实验研究。结果表明:平均应力、应力幅值和应力比等外部因素会对棘轮行为产生较大影响。
相比于大部分传统低强度钢材,TRIP钢是一种多相材料,在受到外部载荷作用时会发生残余奥氏体向马氏体转变,使得在变形过程中的力学行为和微观组织变化更加复杂[9-10]。目前国内外学者关于TRIP钢的大多数研究都集中在合金元素含量[11]以及临界退火步骤[12]对其性能影响,对棘轮特性研究还很少。而TRIP钢多用于汽车、铁路等行业,在实际工作时不可避免会承受非对称载荷的作用,因此,有必要对TRIP钢的棘轮行为进行研究。同时,TRIP钢在变形过程中会发生马氏体相变,导致其棘轮行为特性有别于其他钢材,如果直接沿用传统的本构模型对其棘轮行为进行描述,将难以获得令人满意的结果。因此,还需要对传统本构模型进行改进以合理描述TRIP钢的棘轮行为。
笔者以中锰TRIP钢为研究对象,首先在室温下对中锰TRIP钢的棘轮行为进行了实验研究,然后基于实验揭示的棘轮行为演化规律,对现有的宏观唯象本构模型进行改进,最后将本文模型的预测结果与实验结果进行了比较,验证了模型的合理性。
1 材料和方法
实验选用的材料是中锰TRIP钢,其组成部分(重量百分数, % )为:Mn 6.9,Al 3.2,C 0.35,其余为Fe。材料试样为实心圆棒试样,其工作段长度为20 mm,直径为6 mm。在MTS809-250 kN电液伺服控制实验机上进行实验,测量应变的仪器采用标距为25 mm的单轴应变引伸计,利用Teststar控制系统对实验过程中产生的数据进行采集。在室温下开展了单轴拉伸实验和棘轮实验,应变率和应力率分别为1×10-2/s 和200 MPa/s。
2 实验结果
2.1 单轴拉伸实验
单轴拉伸实验得到的应力-应变曲线如图1所示。实验测得中锰TRIP钢弹性模量E=190.5 GPa、屈服强度σy=601.4 MPa、抗拉强度σb=854.4 MPa。
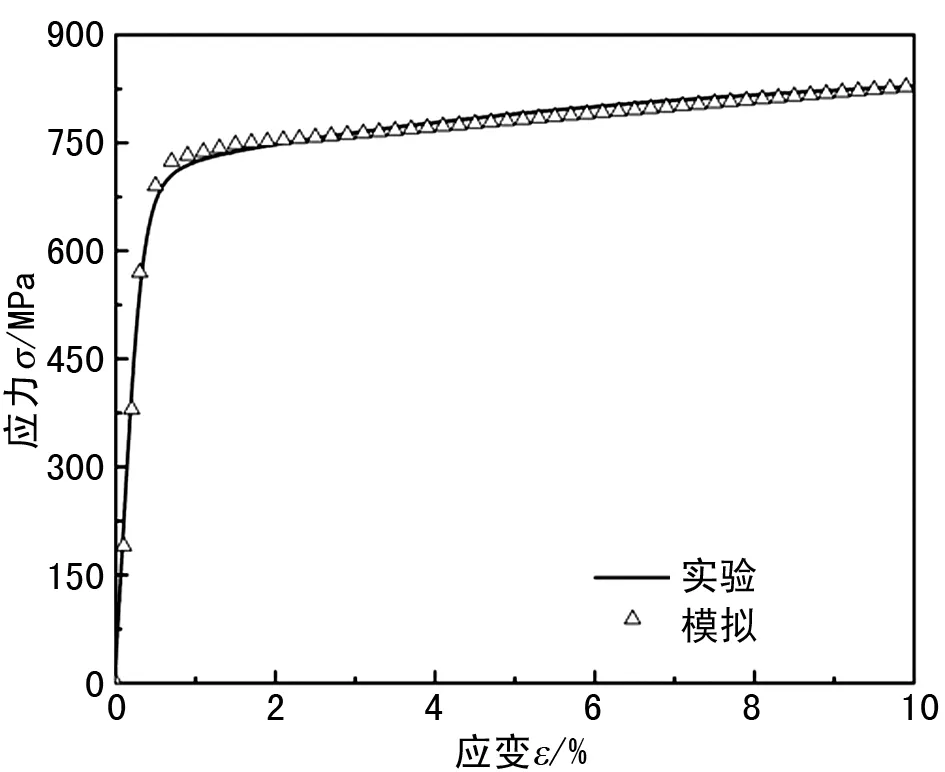
图1 单轴拉伸应力-应变曲线
2.2 棘轮实验
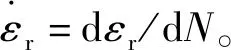
从平均应力为50 MPa不同应力幅值下的结果(见图2)可知:在恒定的平均应力水平下,随着应力幅值的增大,材料的棘轮应变也随之增大,应力幅值对中锰TRIP钢的棘轮特性影响较大。可以看出,当应力幅值较低时(630 MPa、650 MPa、660 MPa),材料的棘轮行为与循环稳定金属材料的棘轮特性相似[13],在循环过程中棘轮应变率“由大变小最后保持为常数”;而超过一定应力幅值时(670 MPa),棘轮应变会出现一直加速的现象,在10圈过后,棘轮应变率一直不断增大,这一特性又与循环软化金属[14]材料的棘轮特性相似。也就是说,在不同的应力幅值下,中锰TRIP钢的棘轮演化呈现出两种不同的特性,这与传统的金属材料有较大差别。产生这种现象的原因可能是在棘轮变形过程中发生了残余奥氏体的相变,相变应变与棘轮应变交互作用导致了棘轮应变率的持续增长,这还需要进一步的微观实验验证。
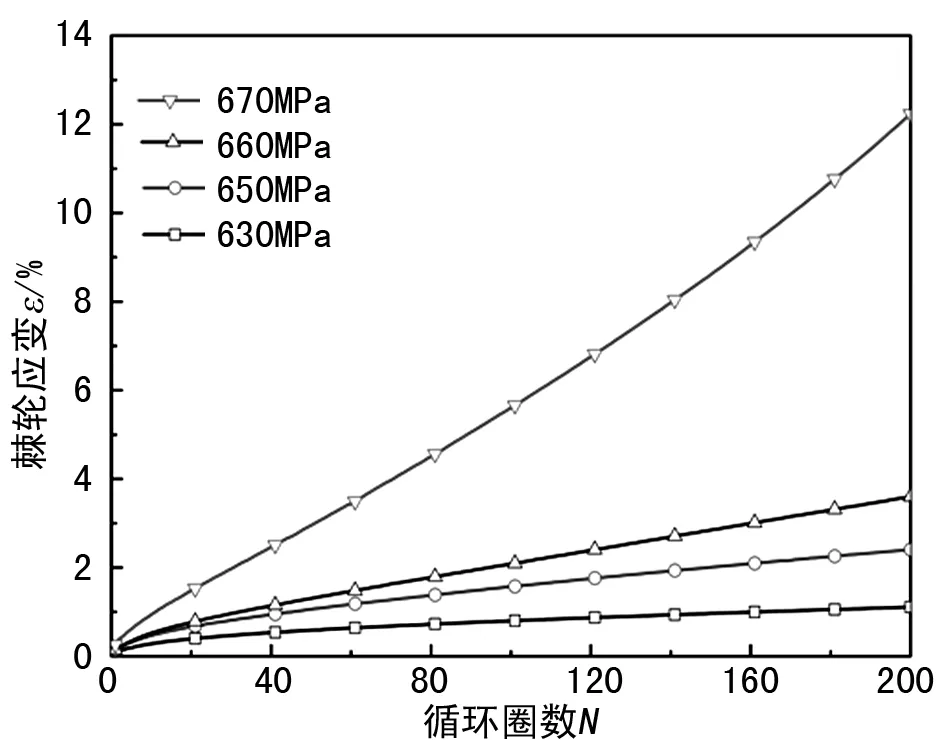
图2 平均应力为50 MPa不同应力幅值下前200圈棘轮应变-循环周次曲线
应力幅值为630 MPa不同平均应力下的棘轮应变-循环周次曲线(见图3)表明:在恒定应力幅值630 MPa下,随着平均应力的增加,棘轮应变随之增加,但棘轮行为演化规律是类似的,即棘轮应变率都是由大变小最后保持常数。
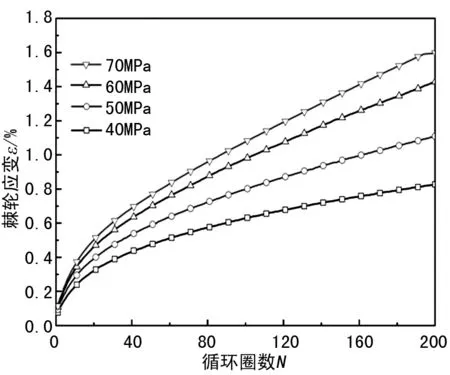
图3 应力幅值为630 MPa不同平均应力下前200圈棘轮应变-循环周次曲线
3 循环塑性本构模型
3.1 主控方程
为了对中锰TRIP钢的棘轮行为演化规律进行合理描述,文中采用了统一塑性理论框架下的弹塑性本构模型,具体方程如下:
ε=εe+εp
(1)
σ=De:εe
(2)
(4)

3.2 随动硬化律
张娟等[15]将A-F模型和Ohno-Wang模型Ⅱ进行叠加,叠加后的背应力演化方程表达式如下:
(5)
式中:α是总背应力,它可以由M个分量求和得到,表示为α(i)(i=1,2…M)。
(6)
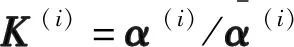
材料常数的计算式为:
(7)
i=1,2,3…M
(8)
式中:σ0为塑性应变为零时对应的应力值,即图4中实验曲线与纵坐标的交点。

图4 单拉应力-塑性应变实验结果及参数确定示意图
μ(i)是棘轮参数,可以通过对单轴棘轮实验数据进行多次拟合,找到最优参数。张娟等[15]将μ=μ(i)取值考虑为常数,采用这个模型对中锰 TRIP 钢的棘轮行为进行描述,发现该模型的预测结果不是很理想,尤其是与50±670 MPa 载荷下的实验结果相差较大。考虑到中锰TRIP钢在发生较大变形时可能发生相变,导致棘轮应变快速增加,文中根据实验结果得到的棘轮行为演化规律,认为棘轮参数μ是一个变量,其演化方程表示为随累积塑性应变指数变化:
μ=μ0eH(f)ap+μ1e-bp
(9)

3.3 各向同性硬化律
各向同性硬化律用来考虑材料的循环软/硬化特性,演化方程具体如下所示:
(10)
(11)

3.4 参数确定
分析实验数据,获取参数步骤如下。
(1) 利用单轴拉伸实验获得,E、σy和泊松比ν。
(2)ζ(i)与r(i)可以通过单轴拉伸应力应变关系获得,方法见文献[16]。
(3) 利用单轴拉伸得到各向同性变形抗力初始值Y0,通过Ysa=Y0+ΔY计算得到Ysa,其中ΔY为各向同性变形抗力增量。在应力控制的循环实验里,应变幅值一般都比较小,因此Ysa可以通过应变幅值最小的实验来确定。利用单轴循环σmax~p关系求γ,假设关系为:
σmax=f1+f2[1-exp(-γp)]
(12)
拟合曲线就可得参数γ。
(4) 棘轮参数μ0、μ1、a、b和R与材料的棘轮行为密切相关,只影响本构方程对材料棘轮行为部分的模拟,因此根据特定工况下的单轴棘轮行为的实验数据,由试错法可以得到。参数见表1所列。
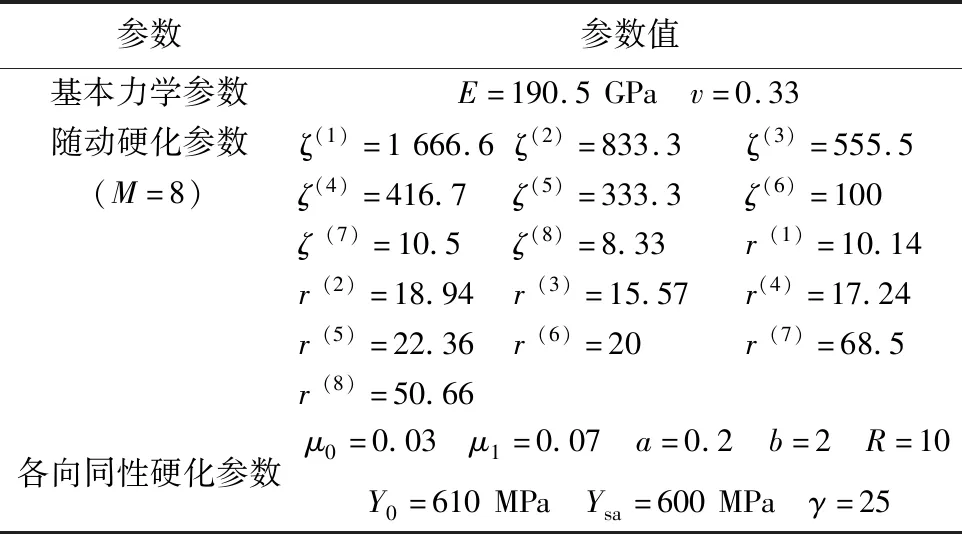
表1 中锰TRIP钢材料参数
4 模拟结果与讨论
采用第3.4节确定的循环塑性本构模型参数对中锰TRIP钢的单轴拉伸、棘轮实验进行模拟。单轴拉伸模拟结果如图1所示,模拟结果与实验结果对比表明:采用的循环塑性本构模型能够较好地预测中锰TRIP钢的单轴拉伸实验。
图5、6分别给出了应力控制循环下不同加载工况的实验结果与本构模型的预测结果。为了进行比较,图中还给出了其他模型的预测结果,模型 1为张娟等[15]模型,其中棘轮参数μ取为常数,模型 2为樊译璘等[17]模型,其中棘轮参数μ是一个变量。
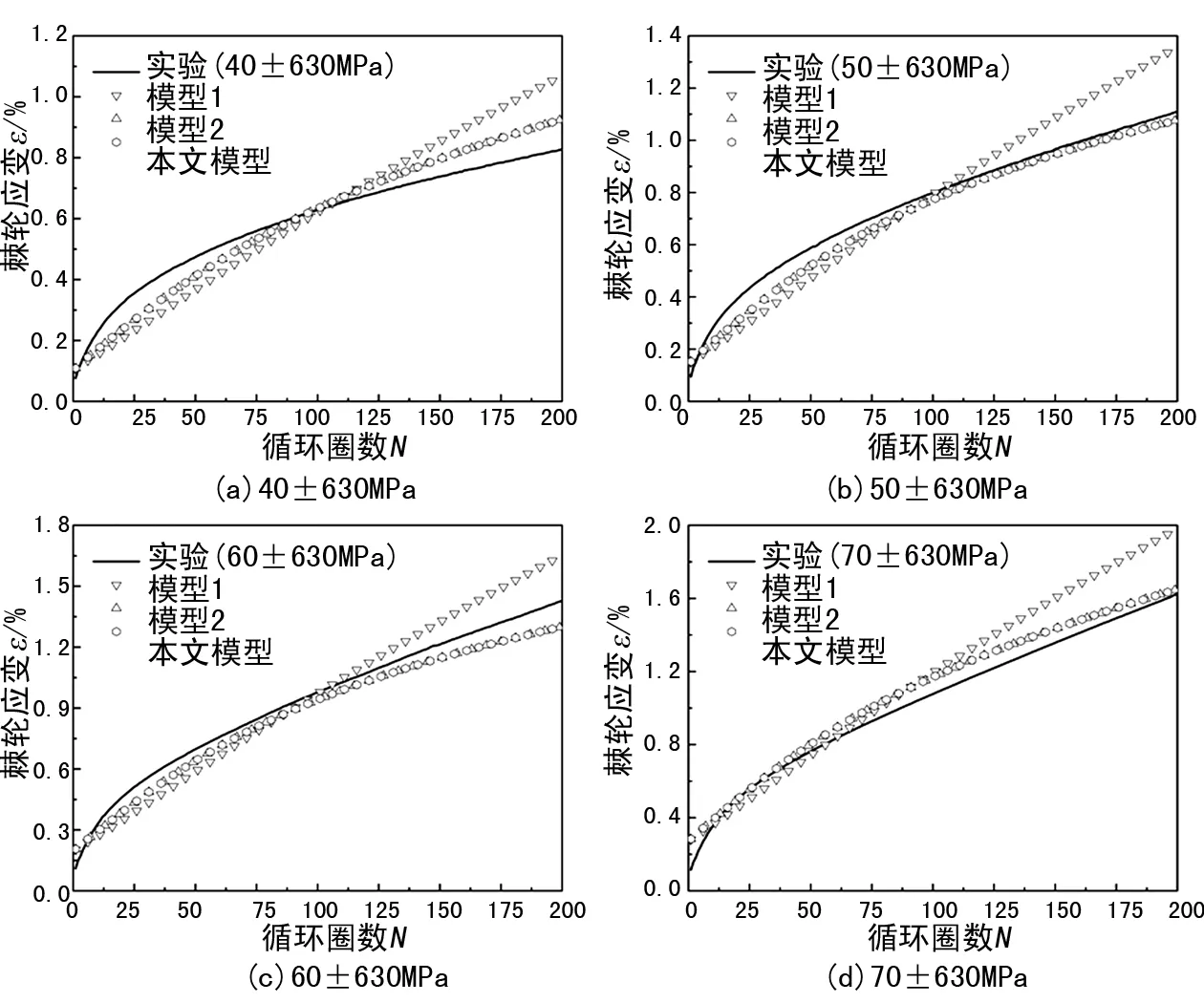
图5 不同平均应力下各模型模拟结果对比
从图5可以看出,模型1模拟的棘轮应变率基本保持为常数,不能对材料棘轮应变率以及棘轮应变变化趋势进行很好的预测。模型2和文中模型对中锰TRIP钢低应力幅值下的棘轮应变演化规律可以给出较好的预测。
从图6可以看出,模型1模拟的棘轮应变率仍然保持为常数,预测能力不足。模型2的预测能力随着应力幅值的增加逐渐变差,当外加载荷为50±670MPa时,预测结果与实验结果相差很大。文中模型模拟结果与材料因应力幅值加大,棘轮应变快速增加的现象一致,模型可以预测材料后期棘轮应变快速增长。
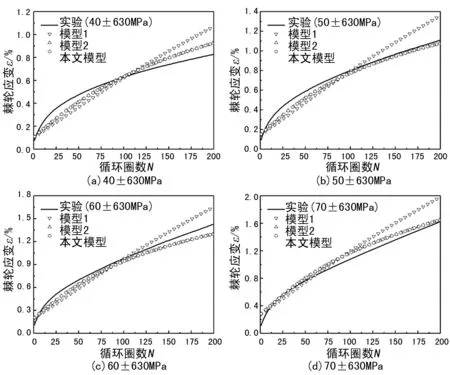
图6 不同应力幅值下各模型模拟结果对比
5 结 论
文中通过一系列非对称应力循环实验研究了中锰TRIP钢的棘轮行为,基于材料棘轮行为特点,对本构模型进行改进,得到如下结论。
(1) 通过室温下的单轴拉伸和棘轮实验数据,揭示了中锰TRIP钢的棘轮行为演化规律。实验结果表明,在不同的应力幅值下,材料的棘轮演化呈现出两种不同的特性:当应力幅值较低时,棘轮应变率由大变小最后保持为常数;而超过一定应力幅值时,棘轮应变会出现一直加速增长的现象。
(2) 将累积塑性应变和阶跃函数引入棘轮参数演化方程中,对循环塑性本构模型中的背应力演化方程进行了改进。对单轴拉伸和棘轮实验结果进行了模拟,模拟结果与实验结果对比表明,文中提出的模型可以更合理地预测中锰TRIP钢的棘轮行为。

