振动过滤离心机系统的动力学特性研究*

何进宝，李万祥，李雄兵，郭雄雄，吴应金,2

(1.兰州交通大学 机电工程学院，甘肃 兰州 730070； 2.中国铁路兰州局集团有限公司 兰州西车辆段，甘肃 兰州 730070)

0 引 言

振动过滤离心机作用是通过固液分离实现产品干燥，主要用于选煤厂脱水等工业领域[1]。文献[2]对离心机内的物料进行了受力分析,给出了计算各种力的方法。文献[3]建立振动离心机的双质体动力学模型，研究了物料进入离心机时所产生的惯性力对系统的影响。文献[4]研究了一种双质体卧式振动卸料离心机弹簧性能，确定了一类卧式振动卸料离心机橡胶弹簧的结构和工艺参数。文献[5]研究了近共振离心机的非线性振动特性。文献[6]建立了振动离心机的四自由度模型，研究了自同步理论。文献[7]对卧式离心机振动系统进行数值计算，发现了系统在简谐激励的作用下存在着倍周期分岔、Hopf分岔和混沌。文献[8]研究了一类二自由度塑性碰撞，在冲击瞬间定义了变量的三维映射。文献[9]研究了两自由度系统周期碰撞运动，讨论了Hopf分岔和混沌现象。文献[10]～[12]对于含间隙系统的分岔、稳定性和混沌进行了详细研究。目前，针对振动离心机理论研究比较少[5]，笔者针对选煤厂脱水干燥设备中的振动过滤离心机进行数值仿真计算。首先，讨论间隙弹簧对于转子系统的振幅与频率的影响，其次讨论不同的参数下系统的分岔和混沌等运动行为。这些讨论将为振动离心机的制造和参数设计提供一些参考。

1 力学模型及运动微分方程的建立

图1所示是一种用于选煤厂脱水的振动离心机。

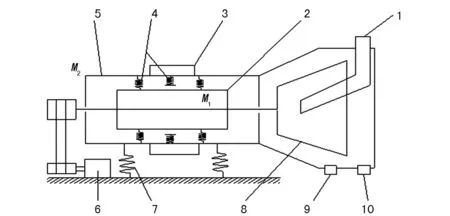
图1 振动离心机结构示意简图1.进料口 2.轴承转子系统 3.激振电机 4.主振弹簧(含间隙缓冲弹簧和环形橡胶弹簧) 5.机壳 6.电机 7.基础隔振弹簧 8.筛篮 9.排料口 10.排液口

振动离心机在离心力的作用下进行分离干燥。物料从进料口进入离心机筛篮窄面，筛篮内的物料在离心力的作用下紧贴筛壁，物料在转子系统激振力轴向振动的作用下，将产品移动到筛篮宽截面，脱水后向排料口排出。水则通过重力最终从离心机流出[1-3,6]。

图2所示是两自由度含间隙弹簧振动过滤离心机系统的力学模型简化图。

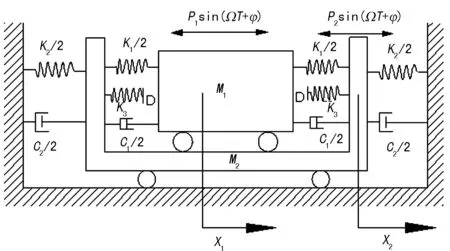
图2 振动离心机系统动力学模型简化图

图2中，M1和M2分别为转子系统(主振体1)和壳体(隔振体2)的质量；X1，X2分别为振体1和振体2水平位移；K1为振体1与振体2的间环形橡胶弹簧在水平方向的刚度；K2为振子2与基础之间隔振弹簧在水平方向的刚度。主振体和隔振体分别由C1与K1和C2与K2的线性阻尼器和线性弹簧相联接，并分别受到简谐激振力(Pisin(ΩT+φ),i=1,2)的作用。由于振动过滤离心机两缓冲弹簧之间存在一定的间隙，所以当振体1和振体2的相对位移≥D时，将与右边弹性约束K3接触，经过运动一段时间改变速度方向后，又以新的初值运动；当振体1和振体2的相对位移≤-D时，将与左边的弹性约束K3接触，经过一段时间改变速度方向后，又以新的初值运动，然后再次与右边弹性约束K3碰撞，如此往复运动。

由牛顿第二定律，振动离心机系统的运动微分方程可以表示为：

(1)

其中：

(2)

为方便计算，将方程(1)、(2)归一化后引入系统的无量纲参数：

则系统的无量纲运动微分方程为:

(3)

(4)

根据以上系统运动状态方程，可对其进行数值仿真计算。

2 振动离心机系统动力学的数值仿真分析

2.1 间隙弹簧特性对主振体的频幅影响

由于振体1和振体2之间存在含间隙的弹簧，它是一个分段非线性弹簧。为研究其对振体1频幅特性的影响，暂时忽略隔振壳体的影响，则振体1的运动方程为：

(5)

(6)

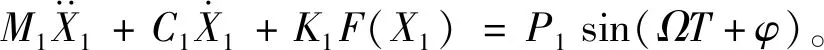
(7)

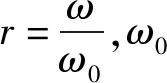
含间隙弹簧引起了系统的非线性。为研究间隙弹簧不同间隙对于振体1频幅特性的影响，当uk3=1时，利用工具箱cftool-Liner Fitting分别取D=0.7,0.9,1.2时拟合参数α,β的值，画出不同间隙D的离心机幅频特性曲线。如图3所示，当刚度比uk3一定时，间隙D取不同的数值，幅频特性曲线其幅值大小的变化趋势大致相同。当频率比r达到一定数值会出现幅值的跳跃，从而引起振体1振幅的振荡。在一定条件下，随着弹簧间隙D的增大，振体1振幅值增大且左移，这对于离心机脱水工作有一定好处。

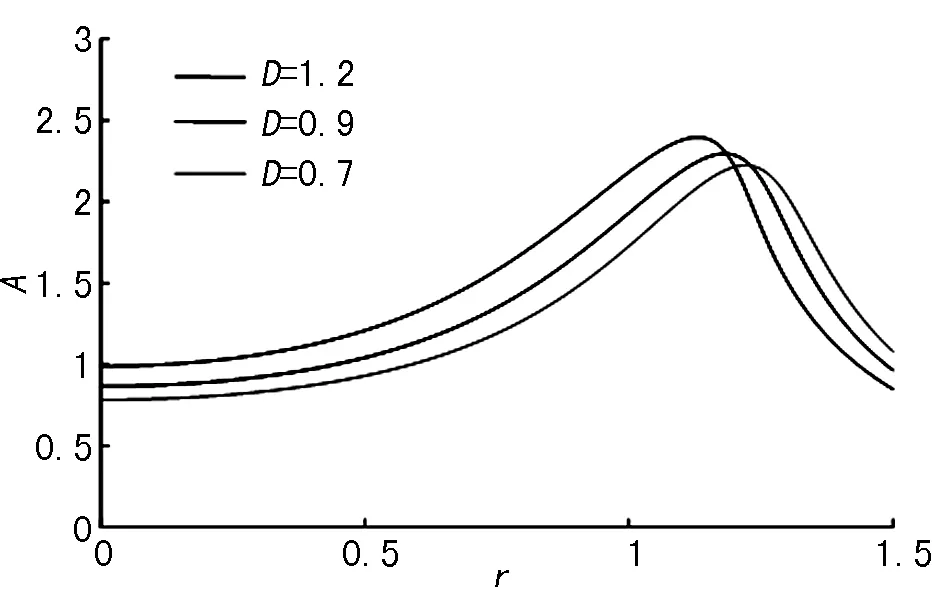
图3 不同弹簧间隙对振体1幅频的影响

为研究不同分段线性弹簧刚度比对振体1频幅特性的影响，当D=0.9时利用MATLAB分别获取uk3=0.7,1,1.3的时拟合参数α,β的值，从而画出不同刚度比uk3的离心机幅频特性曲线。如图4所示，在一定条件下，当弹簧间隙D一定时，相同频率比下刚度比uk3越大振体1的振幅越小，其峰值相对也越小且右移，系统相对来说比较越稳定。

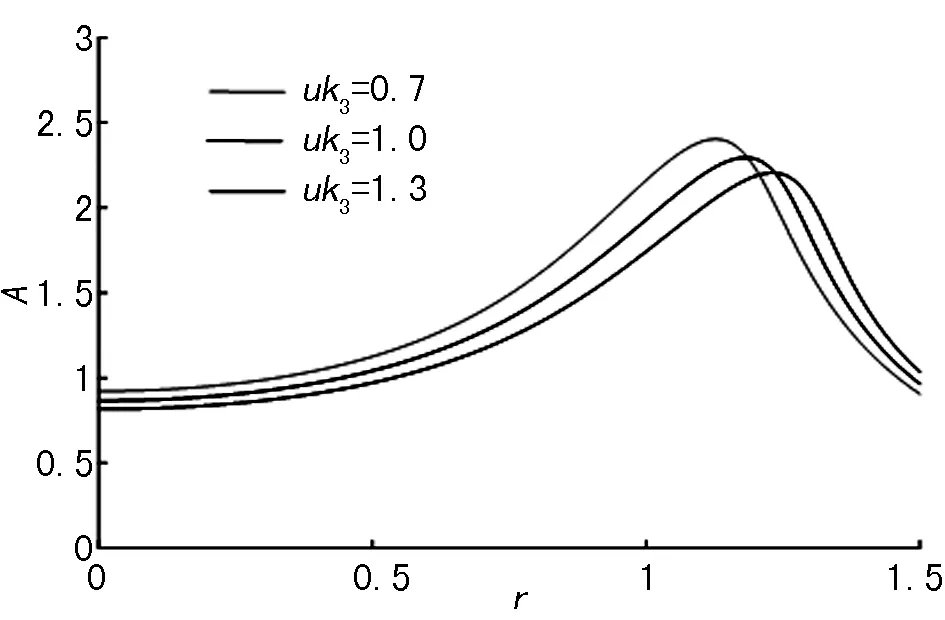
图4 不同弹簧刚度比对质体1幅频的影响

2.2 不同参数下系统分岔与混沌的特性

振动过滤离心机系统在不同参数下，其运动状态也在随时间变化，这些运动有可能是单周期的、多周期的、概周期的或混沌运动。系统将伴随着复杂的分岔和混沌行为。

2.2.1 系统的倍周期分岔与混沌分析

取系统的一组参数μm=5、μc=1.5、μk2=0.01、μk3=30、d=0.01、ζ=0.21、f20=0，以无量纲激振频率ω为分岔参数，用变步长四阶Runge-Kutta法数值计算出m1在ω∈[1.88,2.35]的位移动态响应局部分岔图，如图5所示。

图5 分岔图

由分岔图5可知，系统在ω=1.90附近发生了倍周期分岔，分岔的过程为单周期运动→二周期运动→四周期运动→八周期运动→多周期运动→2nTP→混沌运动。当ω继续增大时系统发生逆倍化分岔，在ω=1.99附近时系统由四周期变为两周期运动。当ω继续增大时系统依次经过混沌激变、逆倍化分岔、多周期运动，最终变为稳定的单周期运动。值得注意的是在图5出现的混沌区域中，可以清楚的看到ω取值在一些狭窄的范围内出现了周期振荡，这些周期振荡称为混沌区内的周期窗口，由此可见系统存在着复杂的动力学特性。

在上述参数不变的情况下从相平面图和Poincaré截面图分析系统ω∈[2.18,2.35]的非线性动力学特性，如图6所示。

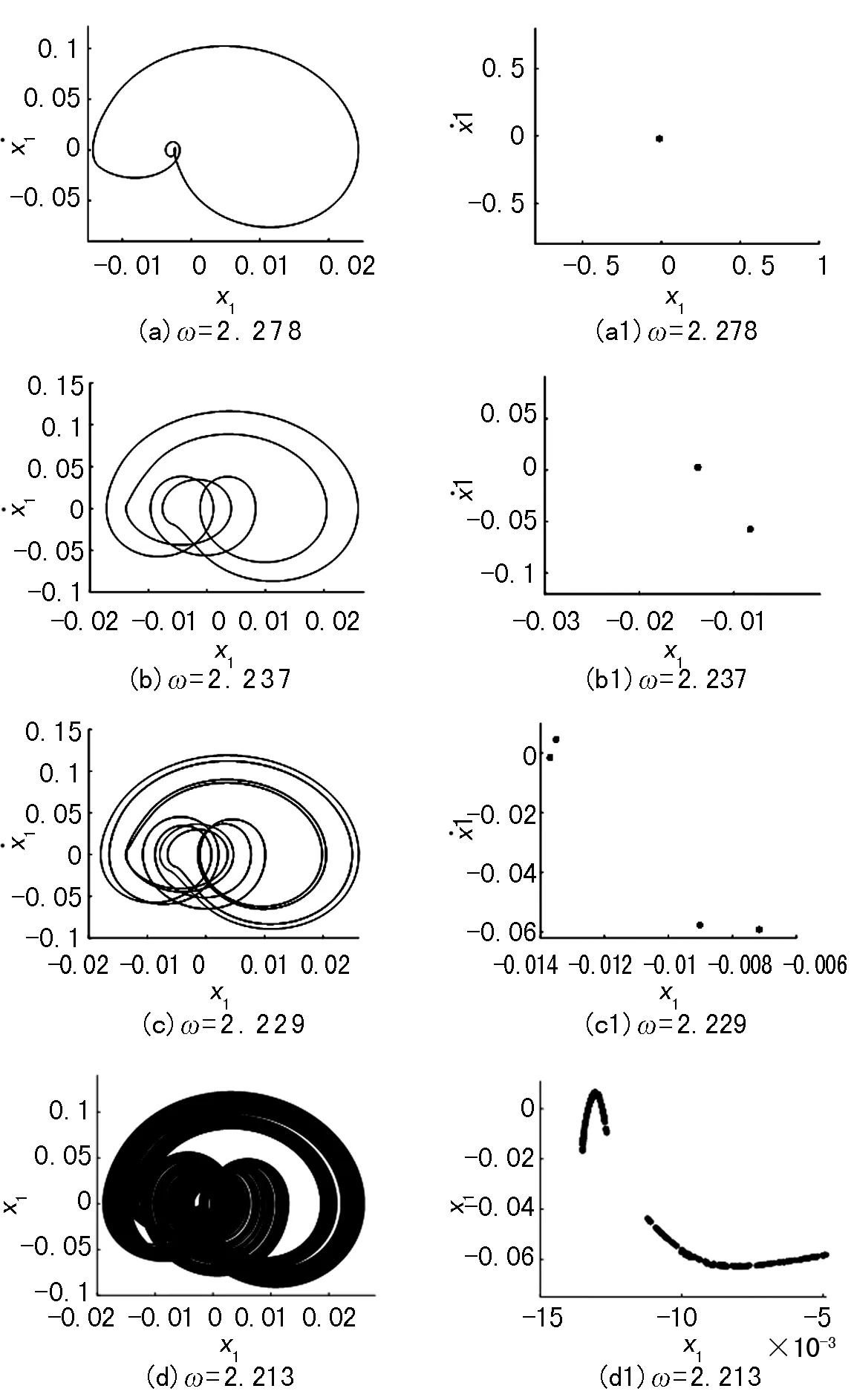
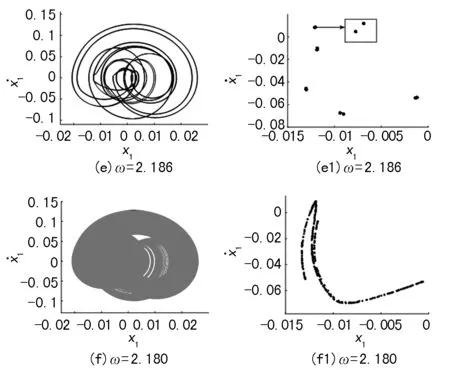
图6 相图和Poincaré截面图

图6(a)、(a1)为激振频率ω=2.278时系统的相图和Poincaré截面图，这时系统做稳定的单周期运动；随着激振频率的减小，系统在ω=2.276附近发生倍化分岔，此时系统做2周期运动，激振频率ω=2.237时的相图和Poincaré截面图如图6(b)、(b1)所示。当激振频率减小到ω=2.234时，系统再次发生逆倍化分岔，做周期4运动，如图6(c)、(c1)所示为ω=2.229相图和Poincaré截面图。依此类推，当ω=2.2附近时，系统出现非周期的稳态响应，系统经过倍周期分岔道路进入混沌响应状态，ω=2.213的相图和Poincaré截面图如图6(d)、(d1)。当ω∈[2.185,2.188]时出现了上述提及的周期窗口，在周期窗口内取ω=2.186的相图和Poincaré截面图，如图6(e)、(e1)所示为10周期运动。当周期窗口结束时，系统运动再次进入混沌运动，如图6(f)、(f1)所示。由图6(d1)和(f1)可以看出混沌吸引子由两个变为一个，可推测在此过程中混沌发生了内部激变。

2.2.2 系统的Hopf分岔分析

取系统的另一组参数μm=5、μc=0.01、μk2=5、μk3=12、d=0.6、ζ=0.21、f20=0。在ω∈[1.4,1.88]的位移动态响应局部分岔图结果，如图7所示。

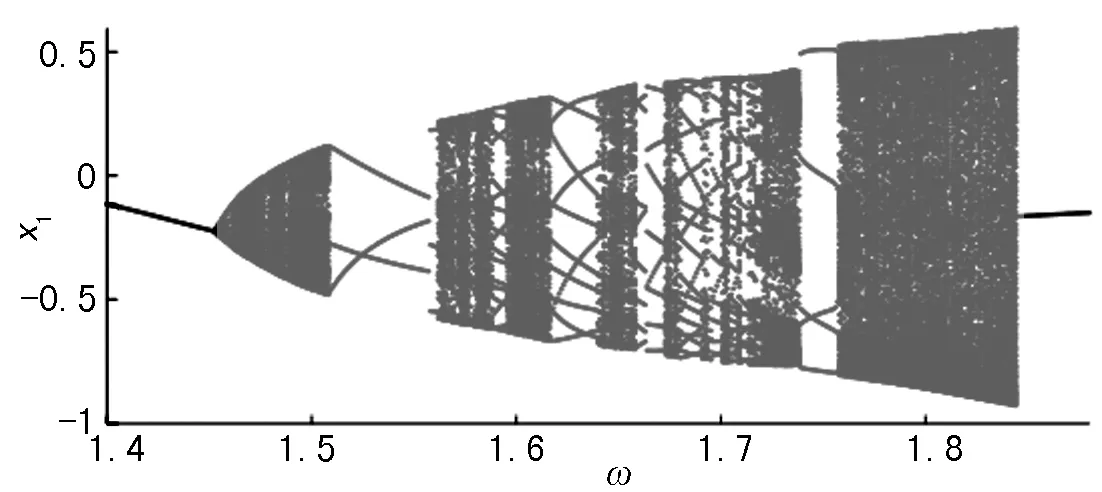
图7 分岔图

由图7可知系统在ω=1.451附近由单周期发生了Hopf分岔，从而系统进入了概周期运动。ω=1.51附近时由概周期突变为三周期运动，随着ω的增大系统经历了多次跳跃、突变，存在多周期、概周期和混沌运动，最终系统突变为稳定的单周期运动。

在上述参数不变情况下从Poincaré截面图分析系统在ω∈[1.4,1.61]的局部动力学特性，如图8。

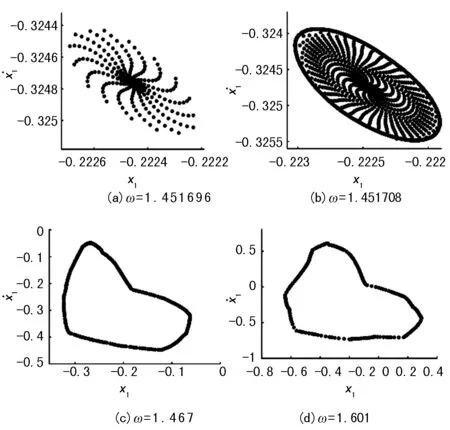
图8 Poincaré截面图

结果表明，当ω<1.451时系统具有稳定的单周期运动，ω=1.451 696时如图8(a)；随着参数ω的进一步增加，在投影的Poincaré截面上形成一个光滑的吸引不变圈，如图8(b)；随着参数ω的逐渐增加，光滑的吸引不变圈开始出现变形，此时系统做概周期运动，如图8(c)；当激振频率ω继续增加，系统为周期运动、拟周期运动的交替过程，如图8(d)。

2.2.3 系统的阵发性分岔与混沌分析

阵发性分岔是系统从周期运动进入混沌运动的一种途径。由分岔图5可知当系统参数ω增加至2.068时，系统由两周期运动发生阵发性分岔进入混沌运动，其相图和Poincaré截面图如图9所示。

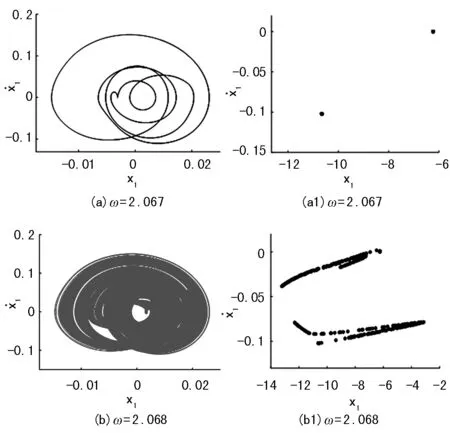
图9 分岔图5的相图和Poincaré截面图

由分岔图7可知，当ω∈[1.65,1.75]时，系统为多周期、拟周期和混沌运动的交替过程，当ω=1.758附近时系统由五周期运动发生阵发性分岔进入混沌运动，其相图和Poincaré截面图如图10所示。

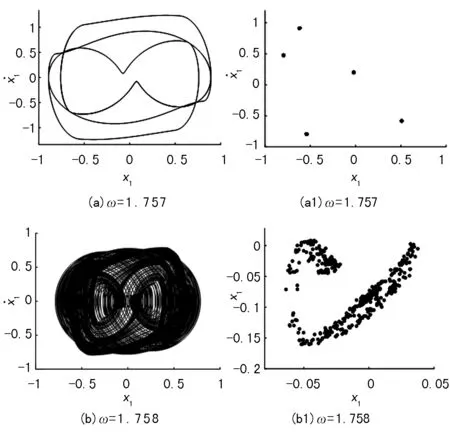
图10 分岔图7相图和Poincaré截面图

3 结 语

文中针对两自由度振动过滤离心机系统的力学模型分析得出：①通过分析间隙弹簧对主振体的频幅特性，在一定条件下，可以通过改变振动过滤离心机的主振弹簧特性来调节主振体频幅，从而提高其工作效率和脱水性能；②对系统进行数值计算仿真，发现了在一定的系统参数下，振动过滤离心机系统具有复杂的动力学特性。采用了分岔图、Poincaré截面图和相图分析了系统倍周期分岔、Hopf分岔，混沌激变，阵发性分岔和跳跃等复杂的动力学行为；③对于该系统混沌与分岔的研究，可在实际中通过优化系统参数来提高工作效率，降低噪声，改善工作条件，使系统工况处于最佳条件。在控制系统混沌运动研究和离心机制造等方面具有一定的理论指导意义和实际参考意义。