液晶屏线路中粘连导电粒子图像分割算法

朱 川 川, 李 忠 奎， 司 俊 文, 谢 蓄 芬

( 1.大连工业大学 信息科学与工程学院, 辽宁 大连 116034；2.大连益盛达智能科技有限公司， 辽宁 大连 116034 )

0 引 言

液晶屏正朝着轻薄智能化的方向发展[1]。异方性导电胶膜(anisotropic conductive film，ACF)因具有小间距、工艺简单、可靠性高等优点，普遍应用于液晶屏的生产制造，成为液晶屏连接的纽带和轻薄化的关键[2-5]。ACF主要由树脂和导电粒子组成，在水平方向上是绝缘的，在垂直方向上是电导通的，称为异方性导电胶膜[6]。在液晶屏制程中，将ACF放置于需要连接的两电极之间，通过高温和一定的压力，将两电极压合，ACF中导电粒子表面的绝缘层会发生破裂并被固化在两电极之间，形成通路，实现极间电流流通，此过程称为ACF热压合。

线路中导电粒子数目多少是决定液晶屏线路导电性能的关键，较少的导电粒子会降低线路的导电性能，可能导致液晶屏出现显示故障；过多的导电粒子，则会造成原料浪费。线路中存在粘连的导电粒子会对粒子计数造成较大的影响，导致计算的粒子数目比实际的数目少，影响检测结果的准确性。

由于粘连目标的多样性，对其分割一直是一个难点[7]。这类问题常用的分割算法有凹点分析法、分水岭和数学形态学等。刘宰豪[8]提出重心辅助凹点的思路，对粘连区域的凹点和重心个数检测和分类，然后通过对应凹点匹配的方式分割目标；孙卫红等[9]通过获取蚕茧轮廓凹凸特征参数序列，提取极小值，筛选凹点相关信息，提出了凹点定向腐蚀的粘连蚕茧分割方法。分水岭是一类使用最为广泛的粘连颗粒图像形态学分割方法[10]。传统分水岭分割图像时往往会产生严重的过分割现象，为了改善过分割现象一些学者提出了基于标记的分水岭方法。靳晓颖等[11]通过优化种子区域，提取分割目标的几何特征，将几何特征与分水岭结合，实现了矿石异物的分割；秦一博[12]对二值化后的粘连颗粒图像进行距离变换，然后在距离变换的基础上进行扩展极大值变换，根据极大值变换获取的标记进行分水岭分割。数学形态学最基本的方法是腐蚀膨胀法。李永峰等[13]通过腐蚀运算层层剥离粘连籽粒，然后使用膨胀运算和八链码恢复大米粒个体，实现分割；罗秋棠[14]在对原图像进行形态学重构的基础上，提取区域极大值，并将极大值作为标记进行分水岭分割，成功实现粘连颗粒图像分离。尽管以上算法针对不同的粘连目标均取得了不错的分割结果，但是在分割粘连导电粒子图像时，均不能取得较好的分割结果。

本研究根据液晶屏线路图像中粘连导电粒子的特点，提出了融入形态学的动态阈值分割算法。该算法引入动态阈值分割图像，以粒子区域灰度特性、形态学几何特征和统计特征为判据获取最佳分割阈值，实现粘连导电粒子图像分割。

1 粘连导电粒子特性分析

热压合后ACF中的导电粒子在电极上表现为一凸起区域，为了区分背景和粒子区域，在成像过程中采用倾斜光照的方式来获得良好的粒子电极图像，也称为管脚图像。在实际的ACF热压合过程中，大部分导电粒子的形变都在合理范围内，具有良好的导电性能；极少部分导电粒子会发生过大或过小的形变，这种不正常的形变严重影响了导电粒子的导电性能，称为不合格的导电粒子。不合格的导电粒子往往具有较大的电阻，对管脚电导通性能的提升十分有限，且造成原料浪费。此外，在热压合后，管脚中存在一定比例的粘连导电粒子和极少数的杂质，并且杂质在面积、周长等方面和粘连导电粒子接近，在筛选和分割粘连导电粒子时容易将杂质误认成粘连导电粒子，造成粒子计数误差。

原始管脚及粒子图像如图1所示。由图1(b)可以看出，导电粒子存在明显的亮暗两个部分，即阳刻和阴刻，在阳刻部分灰度值较高，阴刻部分灰度值较低。图1(c)、(d)、(e)分别给出形变正常、形变过大和形变过小的粒子管脚图像。可知，管脚图像中正常形变的导电粒子占据绝大多数，因此，本研究主要讨论管脚上导电粒子的数量对管脚电导通性能的影响。图1(f)、(g)分别给出管脚图像中存在的粘连导电粒子和杂质。其中粘连导电粒子在管脚图像中的比例约为3%～12%，相对而言，杂质占据的比例极少，同时杂质的灰度均值明显比粘连导电粒子的灰度均值高，可以根据这一特点将杂质筛选出去。

图1 原始管脚及粒子图像

1.1 导电粒子粘连特性

根据粘连导电粒子的特点，将导电粒子粘连情况大致分为三类：强粘连、中度粘连和弱粘连。强粘连是指两个导电粒子粘连程度非常强，即两个导电粒子有超过二分之一的区域粘连一起，单个导电粒子的形状不明显，如图2(a)所示。中度粘连是指两个导电粒子粘连程度较强，即两个导电粒子有一部分区域发生粘连，且发生粘连的区域一般不超过单个导电粒子区域的二分之一，可以较明显地看出两个导电粒子的形状，如图2(b)所示。弱粘连是指两个导电粒子粘连程度较弱，即两个导电粒子仅在边界处存在粘连或粘连区域小于单个导电粒子区域的四分之一，单个导电粒子形状基本保持完整，可以用肉眼很明显的分辨出单个导电粒子的形状，如图2(c)所示。

图2 不同粘连类型导电粒子图像

1.2 导电粒子灰度特征

为了直观显示粘连导电粒子图像阳刻部分和阴刻部分的灰度，以图2为例，分别给出强粘连导电粒子图像、中度粘连导电粒子图像和弱粘连导电粒子图像的三维图像，如图3所示。可知，粘连导电粒子图像阳刻区域和阴刻区域的灰度值存在显著差异，不同类型粘连导电粒子图像的阳刻区域和阴刻区域的灰度分布是不同的。强粘连导电粒子三维图像的阳刻区域和阴刻区域的灰度分布较为紧密，通过动态选取阈值的方式很难实现粘连导电粒子分割；中等粘连导电粒子三维图像的阳刻区域和阴刻区域的灰度分布相对来说较为分散，有一定概率可以通过动态选取阈值的方式实现粘连导电粒子的分割；弱粘连导电粒子三维图像的灰度分布可以看出，阳刻区域和阴刻区域各自都有明显不同的灰度区域。一般来说，大多数的弱粘连导电粒子图像可以通过动态选取阈值的方式实现粘连导电粒子分割。本算法根据粘连导电粒子的灰度特征，采用动态选取阈值的方法对粘连导电粒子图像进行分割。

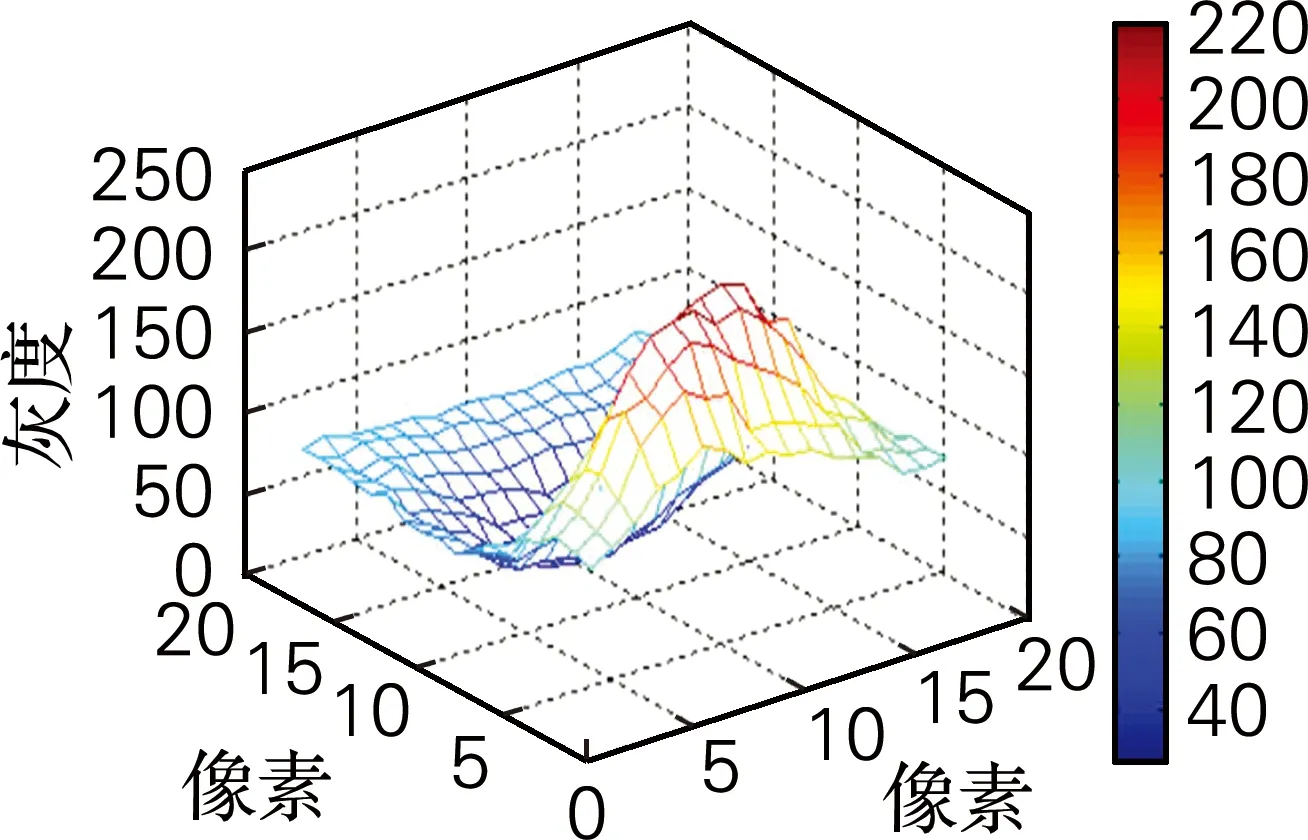
(a) 强粘连粒子

为了提高图像分辨率和方便后续算法处理，对粘连导电粒子图像进行双线性插值放大，双线性插值法是一阶插值法[15-16]。对粘连导电粒子图像作4倍插值放大，经过双线性内插后的图像如图4(b)所示。

图4 原图及插值后图像

ACF中的导电粒子在经过热压合后会发生一定的形变，正常形变的导电粒子在图像中的直

径为10个像素左右，经过双线性插值放大后，粒子直径也增大4倍。选择5×5的模板，依次遍历图像，取模板内像素的灰度均值代替当前像素的灰度，在定位粒子区域时具有较好的表现。均值公式如公式(1)所示。

(1)

式中：f(x,y)表示在(x,y)处的灰度，g(x,y)表示取均值后在(x,y)处的灰度。

1.3 导电粒子统计特征

根据粘连导电粒子图像的特点，利用图像区域的质心个数来确定导电粒子个数。采用式(1)计算质心处的灰度均值并判断质心是否在导电粒子区域，然后通过质心之间的欧式距离来判断质心是否位于不同的导电粒子区域。质心的计算如式(2)所示，欧式距离的计算如式(3)所示。设数字图像f(x,y)，其p+q阶几何矩为

区域的质心坐标为

(2)

设质心1的坐标(x1,y1)和质心2的坐标(x2,y2)，其欧式距离为d。

(3)

2 融入形态学的动态阈值分割算法

针对粘连导电粒子图像的灰度特性和形态特征，提出了融入形态学的动态阈值分割算法。对粘连导电粒子图像进行预处理，采用双线性插值法对图像进行线性放大，对放大后的图像进行最大类间方差处理，获得初始分割阈值T。然后采用动态阈值法对粘连导电粒子图像进行阈值分割，分割阈值从T1=T+1开始，以图像区域的质心个数、质心的灰度均值以及质心之间的距离作为分割图像的判断标准，直到分割阈值T1小于图像最大灰度，若在阈值递增的过程中满足判断标准，则跳转到下一个粘连导电粒子图像进行分割；否则分割阈值T2从图像最小灰度加1开始，分割判断标准同上，直到分割阈值T2=T-1，若在此过程中满足分割判断标准，则跳转到下一个粘连导电粒子图像进行分割，否则转到自适应椭圆结构元素形态学分割法。该方法是在动态阈值法的基础上，针对阈值分割后的图像区域构造自适应椭圆结构元素并使用开运算分割图像区域，若开运算后的图像区域满足动态阈值法的判断标准，则跳转下一个粘连导电粒子图像进行分割，否则记录当前粘连导电粒子图像的序号并跳转到下一个粘连导电粒子图像进行分割。融入形态学的动态阈值分割算法流程如图5所示。

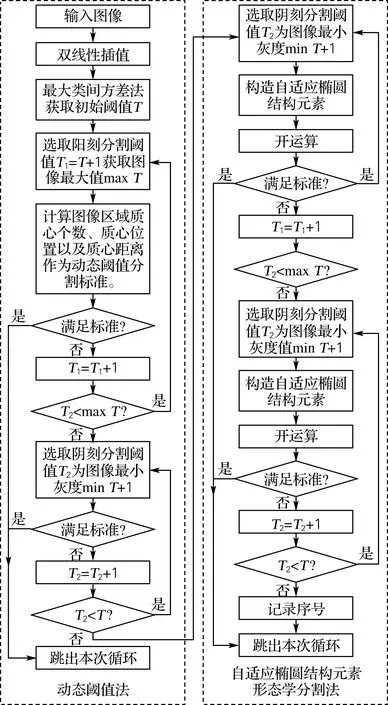
图5 算法流程图

2.1 动态阈值算法

动态阈值法是在最大类间方差法[17]的基础上，分别对粘连导电粒子图像的阳刻部分和阴刻部分进行变化阈值分割，选取最优阈值，分割粘连导电粒子图像。分割的判断标准为，在变化阈值分割图像过程中，要求阈值分割后图像区域的质心个数要大于等于2。在粘连导电粒子图像阳刻部分，要求图像区域质心的灰度均值要大于等于图像最大灰度值的0.6倍；在粘连导电粒子图像阴刻部分要求图像区域质心的灰度均值小于等于图像最小灰度的2倍。图像区域质心之间的欧式距离在10～40内。

2.2 自适应椭圆结构元素形态学分割算法

针对导电粒子粘连类型的多样性[18-19]，提出了自适应椭圆结构元素。获取阈值分割后粒子图像区域最小外接矩形的高和宽，然后将高度和宽度中较大者的六分之一取整作为椭圆的半长轴，较小者的十二分之一取整作为椭圆的半短轴。为了确定椭圆的方向，先确定粘连导电粒子图像区域的方向，使用图像矩求粘连导电粒子图像区域的主轴。

(4)

设一条过点(x0,y0)和x轴夹角呈α的直线为L，则图像区域R关于直线L的转动惯量：

(5)

使I取最小的直线称为区域的主轴。

对式(5)求最小，求导，解方程组得：

(6)

式(6)中α为图像区域R的主轴，则所求椭圆的方向为α。由于椭圆具有对称性，所以将椭圆结构元素原点放在椭圆的中心。将椭圆半长轴(a)、半短轴(b)、椭圆中心(x0，y0)、椭圆的方向α代入椭圆的一般方程如式(6)所示，即可求出椭圆，进而求出椭圆结构元素。椭圆及椭圆结构元素如图6所示。

Ax2+Bxy+Cy2+Dx+Ey+F=0

(7)

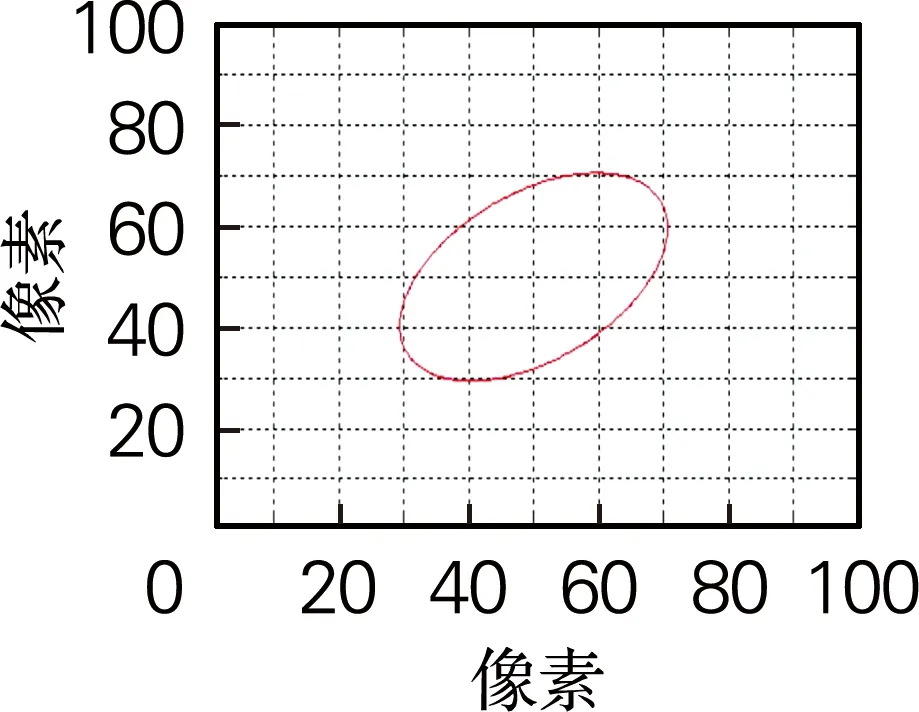
(a) 椭圆

在构造自适应椭圆结构元素后，使用开运算对图像区域进行形态学分割。开运算是先使用结构元素S对目标图像X腐蚀之后，再进行膨胀，定义[20]为

X∘S=(XΘS)⊕S

(7)

针对动态阈值法分割不理想的粘连导电粒子图像，使用自适应椭圆结构元素形态学分割算法进一步分割。自适应椭圆结构元素形态学分割算法，是在动态选取阈值的基础上，针对每一个分割阈值分割后的图像区域构造自适应椭圆结构元素并进行开运算操作，以动态阈值法中的标准作为开运算操作后的判断标准。若满足则转到下一个粘连导电粒子图像，否则记录当前粘连导电粒子图像的序号并转到下一个粘连导电粒子图像，直到遍历所有的粘连导电粒子图像。

3 验 证

为了验证算法的有效性，在win10系统上，利用Matlab2014a测试了某液晶屏线路的50个管脚。在实验测试中使用的PC机配置为Intel(R) Core(TM) I7-8550U CPU 1.8 GHz，内存为8 GB。

3.1 单个粘连粒子图像分割

根据导电粒子的粘连特性，分别选取强粘连程度的导电粒子图像50个，中度粘连程度的导电粒子图像50个，弱粘连程度的导电粒子图像50个，并给出本算法分割后的粒子图像。对于强粘连导电粒子图像，其插值图像及分割图像，如图7(a)所示，中度粘连导电粒子图像的插值图像及分割图像如图7(b)所示，弱粘连导电粒子图像的插值图像及分割图像如图7(c)所示。本研究在文献[12]的基础上，提出标记分水岭分割算法，通过二值图像距离变换方式实现分水岭算法。将图像中每个像素的值变换为这个像素到离它最近的非零像素的距离。具体步骤：(1)对原图像进行双线性差值放大。(2)对放大后的图像进行形态学开闭混合重建运算。(3)对重建后的图像进行双阈值最大类间方差法处理获得二值图像，并对二值图像进行取反。(4)对取反后的二值图像进行距离变换，并获取距离变换后图像的局部极小值，然后对局部极小值进行筛选，去掉伪局部极小值。(5)将筛选后的局部极小值作为标记，并将该标记强制叠加到距离变换后的图像上，然后，对标记后的距离变换图像进行分水岭变换得到最终的分割结果。两种算法的分割结果如表1所示。

图7 粒子图像分割结果

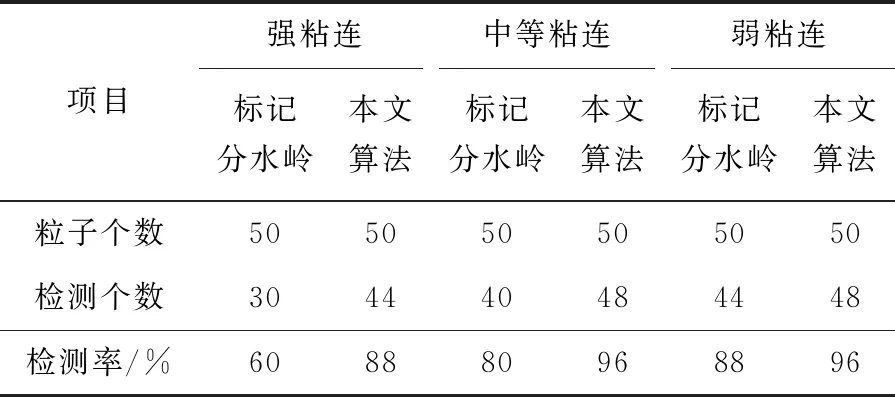
表1 粘连导电粒子分割结果

3.2 管脚图像中的多粘连粒子区域分割

在对单个粘连粒子图像分割后，给出管脚图像的分割结果。在实验中，分别使用“3.1”给出的标记分水岭算法和本文算法对任意选取的50个管脚图像进行测试，取得了良好的分割结果。分割结果如图8所示，其中图8(a)为管脚原图像，图8(b)为粘连粒子筛选图像，图8(c)为标记分水岭算法分割图像，图8(d)为本文算法分割图像。将50个管脚图像按序号1～50标记，单个管脚图像分割结果如图9所示，使用两种算法对50个管脚图像的总体分割结果如表2所示。

图8 粘连粒子分割图

图9 粒子分割结果统计

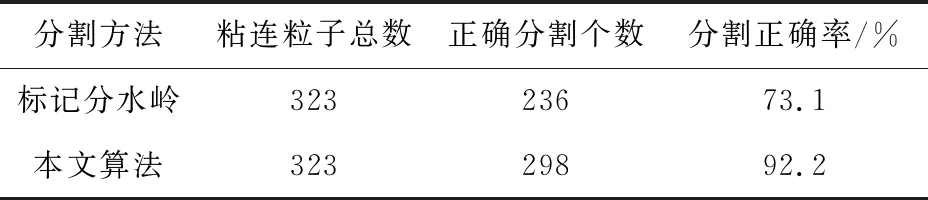
表2 两种算法总体分割结果

3.3 讨 论

使用两种不同的算法对粘连导电粒子图像进行分割，表1为先对150个粘连导电粒子图像进行分类，然后再对其分割的结果进行统计。图9为测试了50个管脚图像的分割结果，表2为50个管脚图像的总体分割正确率。

基于标记的分水岭算法处理流程简单，容易实现，但在粒子分割正确率方面远低于本文算法。由于导电粒子数目多少对液晶屏线路导电性能的优劣起着决定性的作用，所以粘连导电粒子的分割正确率显得特别重要。本文算法有较高的分割正确率，能准确地实现粒子计数，可以有效地判断液晶屏线路导电性能的优劣。

4 结 论

本文提出的融入形态学的动态阈值分割算法，通过使用动态阈值结合形态学的方法，从灰度特性和形状特征两个方面对粘连导电粒子进行分割，取得了良好的分割结果，从而保证了导电粒子计数的准确性，提高了液晶屏线路检测的准确率。