基于改进AlexNet和线性迭代聚类的超像素分割方法
陈 孝 如
( 广州软件学院 软件工程系, 广东 广州 510990 )
0 引 言
图像分割技的本质是把图像根据需要分成相应的感兴趣区域(ROI),每个区域内的像素通常属于具有较小特征差异的同一视觉对象[1]。与图像分割产生的大感知区域不同,超像素分割将图像分割成小的、规则的、紧凑的区域,同时保留基于像素表示的显著特征[2-3]。与图像分割相比,超像素通常具有较强的边界相干性,产生的分割块易于控制。由于超像素在表示和计算上的高效率,超像素被广泛应用于计算机视觉算法中,如目标检测[4]、语义分割[5-6]、跟踪[7]、显著性估计[8-10]。
当前,图像超像素分割方法应用十分广泛且得到很多学者研究[11-13]。学者们对其中的算法进行了创新、探究,其中Achanta等[14]尝试将线性迭代聚类算法应用到图像超像素分割,得到了较为规则的形状,并且各形状大小基本一致,形状与图像的强边缘贴合也表现很好。Achanta等[15]还将非迭代聚类算法应用到图像超像素分割,实现了聚类中心的直接更新。还有一些研究将重点放在精度以及对图像边界的贴合方面,并且出现了多种分层多级超像素算法。Vasquez等[16]提出了一种基于迭代分层随机图收缩的多尺度超像素分割方法。根据图像的多通道特征进行图像初始化分割,然后运用迭代分层随机图收缩方法完成图像超像素分割,并采用分层树表示不同尺度的超像素。Belizario等[17]利用超级像素对图像采取预分割操作,在此基础上根据其颜色信息得到特征,使用边权重表示超级像素之间相似性的度量提出了一种基于加权递归传播(weighted recursive label propagation,WRLP)的图像自动分割方法。Ahn等[18]提出AffinityNet算法,可以预测一对相邻图像坐标之间的语义亲和力,通过使用AffinityNet算法预测的相似度的随机游走来实现语义传播,基于超像素描述符向量之间的距离度量来计算超像素相似度。Salaou等[19]提出了一种新的超像素上下文描述符,以增强学习到的特征,以更好地进行相似度预测。通过迭代合并使用相似度加权目标函数选择的最相似的超像素对来实现图像分割。但以上方法对超像素数目设置较为敏感,如果设置太高则会直接导致过分割问题,反之则会导致欠分割问题。
由于超像素对边界的良好遵守,可以将其视为分割的良好起点。图像分割的结果也可以提供超像素生成的线索,通过将对象级特征集成到超像素分割中,可以达到更好的效果。本研究提出了一种端到端可训练网络,它可以同时产生超像素和进行图像分割,使用简单线性迭代聚类(simple linear iterative clustering,SLIC)算法将超像素生成作为图像分割网络的一部分,取代SLIC算法中的硬像素-超像素关联;通过迁移学习将AlexNet预训练得到的权重用于图像目标的检测,对全连接层参数进行调整,将识别检测视为区分目标与背景的一个二分类问题;训练了一个能够产生准确的超像素的可微分聚类算法模块,并基于生成的超像素执行超像素池化操作以获得超像素特征。
1 超像素的初始分割
与传统的K-平均算法中设置的搜索范围有所不同的是,SLIC算法在确定范围时以2G×2G作为搜索半径,并且G=N/K,N表示的是像素点的个数。图像中任取两个像素之间的距离完全由颜色距离(dc)与空间距离(ds)决定。
(1)
式中:(li,ai,bi)为颜色空间(CIELab)的亮度、红色和蓝色两个颜色通道的颜色偏移量,(xi,yi)为二维空间的坐标值。
超像素将相似像素分组为各向同性区域,可以提高分割质量和效率。使用SLIC算法作为图像分割的开始,将超像素生成作为图像分割网络的一部分,采用可微分聚类算法模块,以取代SLIC算法中的硬像素-超像素关联。对于n个像素点构成的图像,第p个像素点在CIELab中的五维特征可表示为Ip=[x,y,l,a,b],整个图像的特征为I∈Rn×5。将n个像素点构成的图像划分为m个超像素的小区域,在SLIC算法中计算硬像素-超像素关联图H={1,2,…,m}n×1。对于给定的一个统一采样的超像素中心C0∈Rn×5作为初始值,SLIC算法在第t次迭代时分配像素p处新的硬像素-超像素关联图
(2)

由于式(2)中产生了不可微分的最近邻分配,因此SLIC无法直接集成到神经网络中。可微分聚类算法模块将硬像素-超像素关联图H替换为软关联Q∈Rn×m,它相对于输入特征是可区分的。在每次迭代中都有以下两个核心步骤:
像素-超像素关联计算:迭代t中像素p与其相邻超像素i的关联计算如式3所示。
(3)
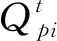
超像素中心更新:新的超像素聚类中心根据像素特征的加权总和得出的,加权计算方式为
(4)
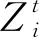
这两步经过多次迭代最终得到软像素-超像素关联Q∈Rn×m。与式(2)类似,计算像素p的显式超像素标签H′p。
H′p=arg maxQpi,i∈{1,2,…,m}
(5)
进而得到硬关联图H′∈Rn×1。这种硬关联的计算是不可区分的。在本算法中,此步骤不参与反向传播。在实验中通过计算每个像素与周围超像素聚类中心之间的距离,减少所有像素和超像素聚类中心之间的软关联距离的计算时间。
2 基于改进AlexNet的超像素分割
为了保证从图像中提取的像素特征保留更多的边界信息,本研究基于网络宽度和深度这两点对AlexNet模型进行了改进。从深度的角度,为了避免出现过拟合问题,减少了模型的层数,同时把全连接层变成了3层。由于单层网络在图像特征学习方面本身较浅,会影响最终结果,所以本研究将网络拓宽,通过两个通道对图像特征进行深度分析。并且两个通道均是3层卷积层结构,第1层的卷积层为两个通道共同使用的部分。再将双通道特征合并至一个层次中,利用3层全连接层得到的抽象特征做进一步分类处理。本研究中的网络通过一个3层双通道的特征融合层以及一个3层全连接层共同构成。输入层要对原始图像进行处理,使其分为224×224×3进而再做出输入操作,224×224为分辨率,3为图像通道数。堆叠层设定为Channel1与Channel2,这两个通道层数以及卷积核完全一致,通过两个通道对图像特征进行获取,再将其传输至分类器。Channel1的卷积核分别为11、5、3,Channel2的卷积核分别为11、3、5,两个通道的卷积核数则均为96、256、384,步长为4、1、1。另外,每层池化核大小均是3×3,步长大小为2,这样设置有利于最后将不同通道特征进行合并。为了避免过拟合问题,在全连接处增加了dropout层。通过K-平均算法主动搜索确定像素标签。本研究的系统框架如图1所示。
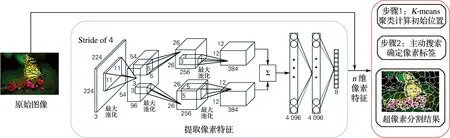
图1 算法概述
2.1 在线超像素生成
AlexNet网络结构如图2所示,AlexNet网络结构相对较为复杂,共包含8层,其中前面5层为卷积层,后3层则为全连接层,并且最后一个将会与softmax层连接。因为这种网络结构需要两个GPU,所以其结构图也包括了上下两部分,其中一个GPU主要用来运行图上方的层,另外一个则主要用于运行下方的层,它们仅仅在一些固定层互有通信。比如,第2、4、5层卷积层的核仅与GPU的前一层的核特征图连接,而第3层卷积层则能够与第2层全部的核特征图相关联,并且在全连接层中的神经元与前一层中的全部神经元同样相连。
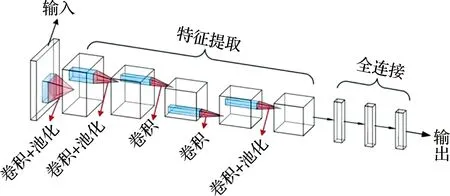
图2 AlexNet模型
由于AlexNet网络采用了两台GPU,所以其速度也相对较快。但是,由最后一个卷积层至全连接层的大小并没有因此而缩小一半,这主要是因为参数多分布在全连接层。卷积层与池化层对于特征获取发挥着重要作用,其具体过程见图3。
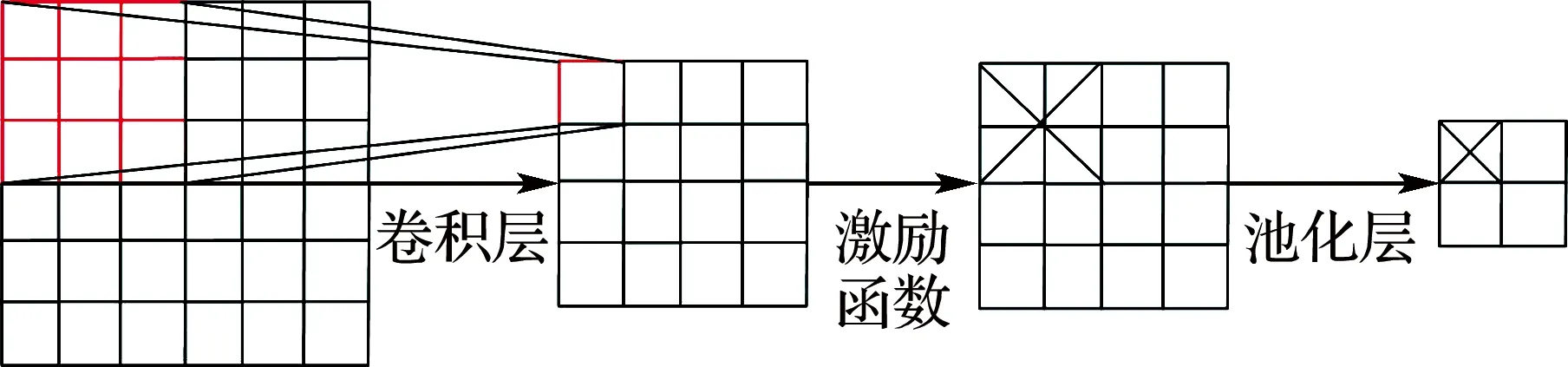
图3 卷积池化示意图
卷积层是由m个卷积核组成的特征映射层。卷积操作公式为
(5)
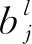
AlexNet模型中采用的是经过修正后的ReLU函数,这种函数为线性函数,它与sigmoid等饱和非线性函数最大的不同在于能够避免梯度消失问题,并且收敛效率也相对较高。在卷积操作完成后将会进入池化层,所以也将其称之为降采样层。其计算过程为
(6)
式中:fp表示池化操作。
AlexNet预训练计算出的权重可以被用来作为识别图像目标的依据,将原卷积层保持不变,再科学设置全连接层参数,通过得到的特征进一步将识别检测转换成目标与背景的二分类问题。连接层参数、训练参数以及避免过拟合(Dropout)参数的调整进一步提升最终结果的精度。
(7)
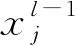
因为优化后的AlexNet的输出与原图尺寸一致,所以可以对分隔层的图层L6、L7科学设置以便能够减少特征维度,从而保证输出尺寸与原图完全一样,输出层则利用ReLU函数。

(8)
2.2 损失函数
假设相同分割区域中的超像素对之间的相似度大于不同分割区域中的超像素对之间的相似度,基于定义的相似性度量,认为损失函数如下:
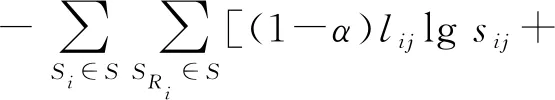
α(1-lij)lg(1-sij)]
(9)
式中:Ri为超像素Si的相邻超像素集合,lij∈{0,1}表示Si和Sj是否属于同一分割区域。在实际应用中,lij为根据得到的超像素集S和数据集提供的真实值分割掩模计算的。当Si和Sj属于同一分割区域时,lij=1;否则,lij=0。
对于不同的输入图像,第(i,j)项被定义为lij的矩阵是不同的。因此,在训练阶段的微型批处理的大小必须设置为1,即一次只能将一幅图像输入网络。α代表属于真实值中相同区域的超像素对的比例,它用于平衡正样本和负样本。将|Y+|表示为属于同一区域的超像素对数,|Y|表示为超像素对的总数,则α的计算方法为α=|Y+|/|Y|。通过反向传播,图像分割也指导了超像素分割。
2.3 像素合并
在本算法算法执行超像素合并时,使用的像素特征与超像素生成中使用的像素特征不同。因为超像素不包含语义信息,而对象分割却包含语义信息,因此这两个任务的合适功能会有所不同。通过表示使用S={S1,S2,…,Sm}获得的超像素集合,通过执行超像素池化以获得超像素特征向量{v1,v2,…,vm}:
(10)
式中:F′p为超像素合并中使用的像素p的特征向量,|·|为集合的基数。
可以通过式(11)计算两个相邻的i和j之间的相似度。
(11)

通过合并相似的超像素获得最终的图像分割,使用相邻超像素之间的相似度和预设阈值T来确定两个相邻超像素是否合并。算法1概述了超像素合并中的计算步骤。
算法1:超像素合并算法
Input:s,相似性
T,相似阈值
S={S1,S2,…,Sm}:超像素
Output:SegmentationS
1: for eachSi∈Sdo
2: Construct adjacent superpixel setRi⊂SofSi;
3: for eachSj⊂Rido
4: ifsij>Tthen
5:Si←Si∪Sj,S←SSj;
6: UpdateRi;
7: end if
8: end for
9: end for
特征提取的AlexNet网络由卷积层、组归一化和ReLU激活组成,将GN中的组数设置为8。在第2层和第4层卷积之后,使用最大池来增加接收场。对第4层和第6层的输出进行采样,然后与第2层的输出串联以丰富提取的特征,使用3×3卷积滤波器将输出通道设置为每层64。
考虑到网络中每个微型批处理的大小必须为1,因此用组规范化(GN)替换了广泛使用的批处理规范化(BN)层。BN是深度学习发展中的一个里程碑式技术,它对各种网络都可以进行训练。但是,由于批次统计信息估计不准确,当批次大小变小时,BN的误差会迅速增加。相比之下,GN将通道划分为多个组,并在每个组内计算均值和方差进行归一化。GN的计算与批次大小无关,并且其精度在各种批次大小中都是稳定的。
对于两个不同级别的任务,即超像素生成和图像分割,进一步对上一步中获得的图像特征执行卷积运算,以获得不同的特征向量以满足不同任务的需求。具体来说,对于超像素生成任务,使用内核大小为3×3的卷积层获得通道特征向量。对于图像分割任务,首先对256个输出通道执行3×3卷积运算,然后使用1×1卷积核获得64通道特征向量。将获得的特征向量分别输入到随后的可微分聚类算法模块和超像素池化层中,然后使用提出的相应损失函数训练网络。
3 实 验
3.1 环境与设置参数
本研究硬件配置为CPU Intel Core i7-3110GM@2.4 GHz,内存4 GB、1 600 MHz,Windows8操作系统。采取2个GPU的配置为Tensorflow 1.12+CUDA 9.0+cuDNN v7.1 for CUDA9.0,GPU:NVIDIA GeForce MX150,本文使用已在图像分割社区中广泛使用的BSDS500数据集作为服务器的训练数据。由于BSDS500中的训练样本数量很少,因此训练时必须增加数据。将每个真实值视为一个单独的样本,并将每对图像和真实值作为训练样本馈入网络。通过这种方式,总共获得了1 633个训练/验证对和1 063个测试对。此外,采用翻转和裁剪策略来实现数据扩充。基本学习速率设置为0.000 1,生成的超像素数量设置为100。动量设置为0.99,以在较小规模的数据上实现稳定的优化,每个小批量的大小设置为1。
3.2 BSDS500数据
BSDS是由美国著名学府加利福尼亚大学伯克利分校的计算机视觉组提出的,其最初主要用于图像分割以及边缘识别,该数据集的得出是通过对1 000张图片进行深度分析得出的标准图像数据库Corel-1000生成的,然后再由30个研究人员对其进行标注,最终获取了12 000张分割分割图单元及图片轮廓。视觉组将这些图片又进行了分类,最终得到300幅彩色图像。BSDS500就是通过500张RGB格式的图片共同组成,其中有200张用于训练集,200张用于测试集,还有100张是用来验证的数据集。
对于超像素生成和图像分割,本文将WRLP算法[17]、AffinityNet算法[18]、RF-MDC算法[19]与本文所提算法在BSDS500数据集上的处理结果进行了比较。图4显示了所提算法与其他算法的比较。图4(a)、(b)显示了本算法的变体与其他变体之间的隔离结果比较。并且所提算法在图像分割中表现良好,并且在边界F度量和时间方面优于其他算法。尽管RF-MDC花费的时间为0.223 4 s,用时最少,但却效果不佳。AffinityNet算法在边界F测度上达到最佳,但比所提出算法慢。可以看出,对于大多数配置,本算法获得的超像素在边界F测度上实现了最佳性能,F-measure为0.693 2 s。超像素将相似像素分组为各向同性区域,从而可以提高分割质量和效率,实现了时间与效果之间的平衡。

(a) 分割时的边界P-R
在图5和图6中进行了一些定性比较,如图5所示,对于超像素分割,WRLP和AffinityNet算法的分割结果的边界是不规则的。本算法的处理效果可以得到更规则的边界和更好的边界粘附性。如图6所示,对于图像分割,WRLP算法、AffinityNet算法和RF-MDC算法的分割结果更加碎片化。训练了一个能够产生准确的超像素的可微分聚类算法模块,并基于生成的超像素执行超像素池化操作以获得超像素特征,分割的结果在视觉上更接近真实。RF-MDC生成的超像素更规则,但缺乏边界黏附。本算法在超像素分割和图像分割方面都达到了较好的水平。

图5 超像素生成

图6 图像分割结果比较
3.3 MRI数据集
实验数据是由多伦多医院影像科提供的,根据33名患者脑部MRI图像序列生成的数据,每个患者均生成8到15个序列,图像中的5 011张是通过手动分割获得的,将其中的4 009张图像作为本次实验中的训练数据集,其余图像用于测试。原始图像为256×256,为了提高计算效率,利用ROI提取128×128的大小,将左心室轮廓进行保存,其余数据不再保留,如图7所示。
将本研究算法用于脑部MR图像的过分割,并与WRLP算法、AffinityNet算法、RF-MDC算法的所得出的结果做比较。合成脑部MRI时一般从Brainweb数据库进行调取,分割的超像素一般是800。图7展示的就是不同算法合成与原MRI图像的对比,以及一些局部区域放大后的情况。从中能够看出,本次所采用的算法所得到的自适应的超像素相对更多,较为平坦的地方超像素具有一定的规律性,在复杂的地方同样能够得到边界。后面的聚类过程中,能够进一步分割出不同小区域的超像素,这也更加便于分割脑组织。
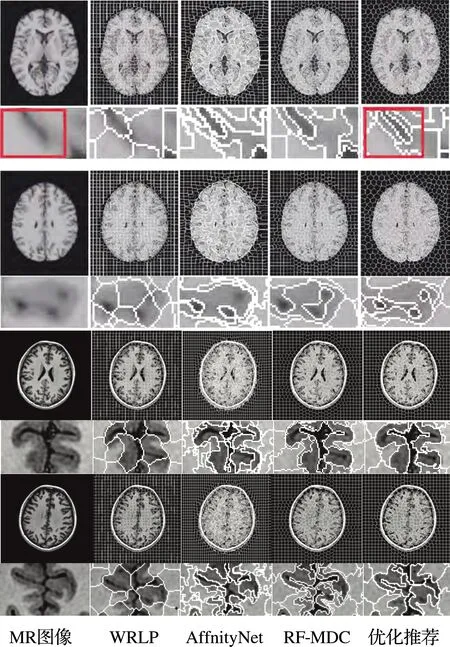
图7 不同算法合成MRI图像的超像素分类结果比较
3.4 超参数分析
使用如图1所示的网络结构作为主要模型(命名为ours-GN8),使用BSDS500数据集来评估网络中每个组件的不同选择。比较GN8的3种变体在超像素生成和图像分割方面的性能,融合BN:将组规范化(GN)操作替换为批处理规范化(BN);融合GN32:在GN期间,将组号设置为32,而不是融合GN8中的8;融合conv7:使用相同的功能(从第7个卷积层(conv7)获得)进行超像素和图像分割。
对图像分割和超像素生成的结果进行了评价。从表1和表2可以看出,原始网络与其他变体相比效果最好,表明本实验选择的组件是合理的。GN解决了BN对批次大小依赖性的影响。对于小批量,GN可以获得更好的效果。但是,当组太多时,效果会降低。根据历史实验数据,浅层网络包含更多详细信息,深层网络包含更多全局信息,并且原始网络提取的特征更多,因此分割效果更好。融合conv7的效果显著降低,融合GN8大大优于融合conv7,从而验证了在多任务学习中,不同级别的任务需要不同的图像特征。
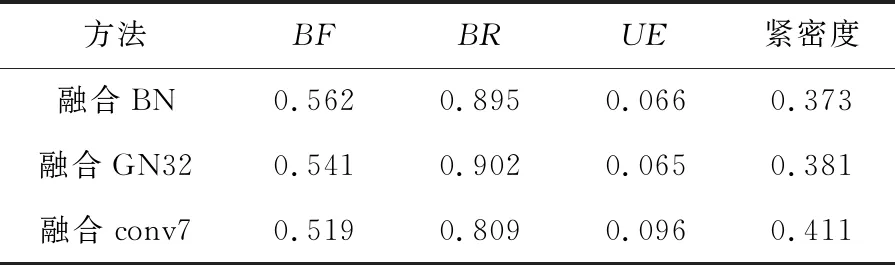
表1 3种变体的超像素生成性能

表2 3种变体的图像分割性能
4 结 论
本研究提出了一种可以生成超像素和图像分割的端到端可训练网络。使用AlexNet网络提取图像特征,使用可微分聚类算法模块生成精确的超像素。通过使用超像素池化操作获得超像素特征,并且计算两个相邻的超像素的相似度以确定是否合并以获得感知区域。所提算法在超像素生成和图像分割方面都取得了良好的性能。此外,由于所提出的算法是端到端可训练的,因此可以轻松地将其集成到其他深层网络结构中。

