智慧型电力应急预案模式在故障线路快速定位方法中的应用研究

李国庆，范晨亮，闫云强，李文燕，李晓飞

（国电电力内蒙古新能源开发有限公司，内蒙古 呼和浩特 010010）

电力作为国民经济的基础产业，对经济社会发展和人民生活起着重要的支撑和保障作用，无论何种突发事件的发生，电力安全都是公共安全中的首要关注对象，这使电力应急预案在电力安全中的地位显得尤为重要[1-6]。但随着电网规模的不断扩大，对预案的实用性、简洁性、可操作性提出了更高要求，现有的电力企业应急预案不断暴露出臃肿、繁杂的弊端。此外，现有电力应急预案大多以静态脚本为基础，忽略了电力事故的发生发展具有随机性这一客观事实，这使得预案响应的准确性和时效性得不到很好的保障。

在电力系统中，极易受突发事故影响就是输电线路，而配电网因其结构的复杂性以及分布式电源的加入，使得其更易受到突发事件的影响，同时保证供电可靠性和安全性的基础也是输电线路的正常工作。针对现有电力应急预案在响应该类电力灾害事故中的准确性和时效性不足，本文提出智慧型电力应急预案下的故障线路快速定位模型，解决了现有应急预案在处理线路故障型突发事故时的准确性和时效性欠缺问题。而随着现代电网大数据技术的不断发展以及FTU（Feeder Terminal Unit）的逐步普及应用，使得实时采集开关信息成为可能，电力应急预案能够根据事态发展趋势做出动态调整，从而构建出具有动态感知能力的智慧型电力应急预案。

基于以上分析，本文构建出智慧应急预案下的故障线路快速定位模型，利用该模型能够快速准确地找出因突发事件导致故障的线路位置，从而提高智慧电力应急预案定位响应对象的时效性和准确性。本文中的方法能够在发生突发事件导致线路故障时，在不切除DG的情况下，快速定位故障线路位置，从而使其能够得到快速的电力应急响应，恢复线路的正常运行。

1 APTS简化模型

1.1 模型基本原理

由经验可知，电力系统中的配电网具有闭环设计、开环运行、网络结构为辐射状等结构特点，在考虑含有分布式电源网络的情况下，电力应急预案准确定位发生故障的线路时，通过将含有分布式电源的配电网络看成是一个有向图，将该有向图中度为1且以电源点（含分布式电源）为顶点的网络连通图定义成有源树，网络中除去有源树后剩下的网络路径则称为无源树，则利用有源树和无源树简化模型（Active and Passive Tree Simplification，APTS），就能够将整个含分布式电源的配电网络划分成包含一个有源树以及多个无源树枝的有向网络。

电力系统中的有源树包含了所有电源（含分布式电源），当配电网因突发事件导致线路故障时，各电源都会产生故障电流，所以在有源树网络中必然存在故障电流的流过，而无源树本身并无电源，即使其上有故障电流流过，也是依靠有源树所提供，当某个无源树无故障时候，整个无源树链的所有节点都没有故障电流通过。因此，能够在定位过程将其去除，从而不予考虑，这样能够一定程度地缩短算法中解的维度，提高计算效率。

1.2 APTS简化实现流程

以IEEE33节点图来对APTS简化模型理论解释，如图1所示，假设线路L30因突发事件导致故障，智慧电力应急预案需要以最快的速度找出故障线路的位置，正常情况下，需要对本系统中33条线路的运行状态进行逐一判断，从而找出实际发生故障的线路位置，若将系统分为有源树和无源树，则无源树L6至L17中均无故障电流流过。因此，能够将其直接去除不予考虑，从而将算法的计算维度从33缩减至21，减少了模型的计算量。

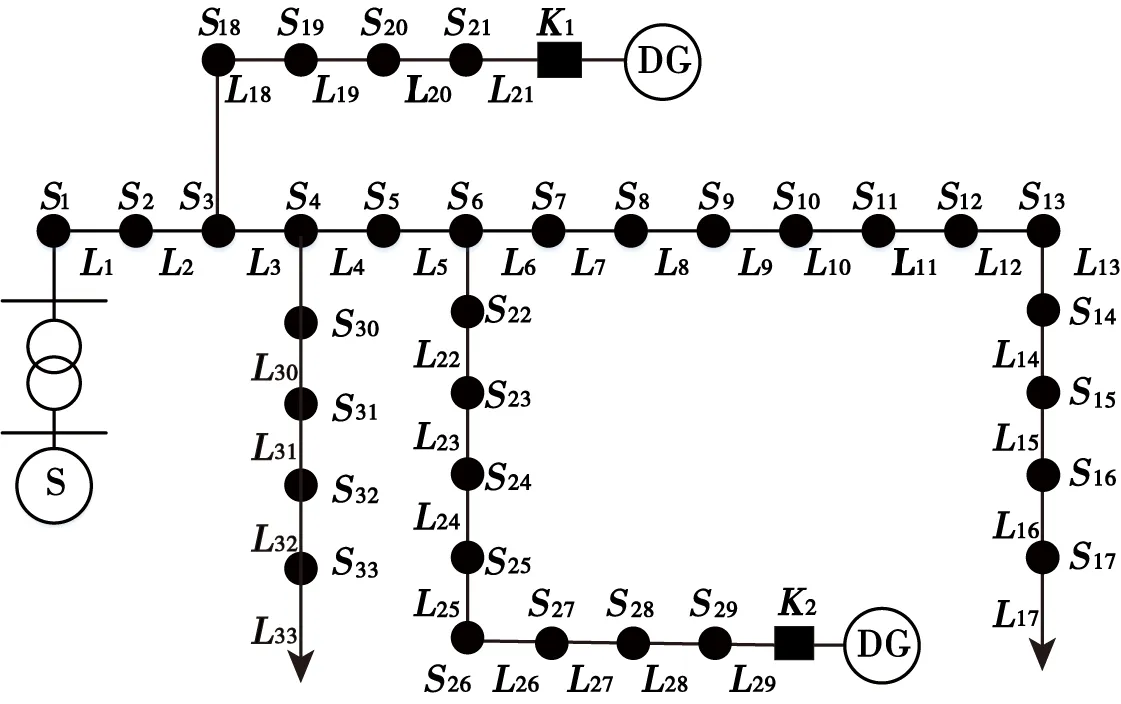
图1 IEEE33节点网络拓扑Fig.1 IEEE33 node network topology

通过上述分析，并结合网络图论知识，本文给出智慧预案下的故障线路定位APTS简化模型流程，如图2所示。

2 遗传算法的改进

2.1 遗传算法

遗传算法（Genetic Algorithm，GA）由密歇根大学的约翰·霍兰德等于20世纪60年代率先提出[7]。遗传算法进入实际应用领域的里程碑，是20世纪80年代中期在匹兹堡召开的第一届世界遗传算法大会，此后，遗传算法开始应用在更多领域。

遗传算法是一种随机全局搜索和优化方法，其原理模仿了自然界生物进化机制[8-11]。根据达尔文和孟德尔的学说，在生物进化的过程中，会变异出各种基因，这些基因本质上没有好坏之分，但是自然环境会淘汰不能使生物体适应环境的基因，而那些能对环境适应性强的基因则会在传递下来。最终，经过漫长的进化过程，生物体身上只剩下能够使其适应环境的性状及其基因。这个进化过程，可以看作一个优化的过程，通过繁衍和进化，最后留下最适应环境的基因组合，使生物体在自然竞争中生存。

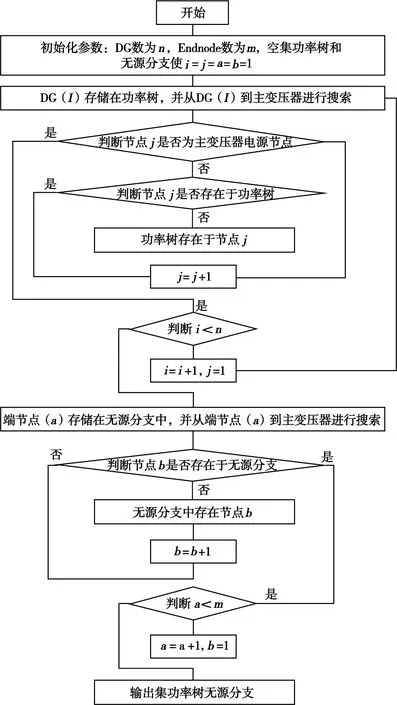
图2 APTS简化流程Fig.2 Simplified flow chart of APTS

在上述思想基础上发展出的遗传算法，其本质是一种搜索方法，能在搜索过程中高效、全局地自动获取和积累有关搜索空间的知识，并在搜索过程中进行调节，最终获得最佳解。

2.2 相似系数的改进

遗传算法中最重要的2个部分是变异和交叉。其中，变异部分直接影响种群是否能够出现新的基因，而交叉能力则能够反映出算法的最优解搜索能力，所以变异概率以及交叉概率的构建合理性对种群的进化具有非常大的影响。

传统遗传算法中引入个体相似系数φ（i）能够反映出第i代种群的相似程度[12]：

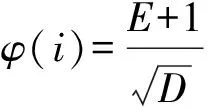
（1）

式中，E为种群适应度的期望值；D为适应度的方差值，反映个体的适应度离散状况。随着种群的不断进化，其对应的期望值会越来越大，方差则会越来越小，从而相似程度就越大，所代表的就是种群不断趋于收敛。

这种相似函数的局限性在于并不具有全局性，种群个体的相似程度仅在进化后期才会影响较大，而在进化前期，种群中个体相似性较小。此时若只用式（1）来表示个体间的相似程度，完全忽略前期种群个体之间的差异性，会影响算法的精确性。为此，本文试图构建一种具有全局性的相似系数，通过把调整因子引入到相似函数中，来弥补传统相似系数在前期的不足，具体表示如下。

（2）

式中，u（i，j）为第i代第j个个体调整因子；fmax（i）、fmin（i）分别为种群个体中第i代个体的适应度最大与最小值；f（i，j）为种群中进行变异、交叉操作的第i代第j个个体适应度。

根据式（2）可以得到新的相似系数为：

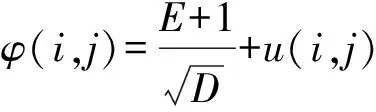
（3）

与传统的遗传算法相比，本文中对相似系数的改进能够使种群在进化过程中，动态地调整算法中的相似系数，从而使种群个体在整个进化过程中都能够按照自身特性以及和其他种群个体的关系进行调整。其中，u（i，j） 主要作用于进化前期，在前期种群个体差异性较大，故反应个体间相似性φ（i）的较小，而反应个体间差异性u（i，j）则对φ（i，j）的影响较大，后期则正好相反。

2.3 概率函数的重构

由遗传算法可知，当种群中个体之间的差异性大时，种群整体的基因类型是非常丰富的，则在算法进行时应当给予当前一代种群比较大的交叉概率和较小的变异概率；反之，如果当前种群个体之间的差异性小时，则应当给予其较大的变异概率和以及较小的交叉概率。

通过以上分析，并结合反正切函数变化趋势可知，反正切函数的性质与上述的基本理论一致，故而利用反正切函数来对遗传算法中的交叉、变异概率函数进行改进，具体如下：

（4）

（5）

式中，Pe（i，j）为种群个体交叉概率；Pm（i，j）为种群个体变异概率；k1、k2、ke的具体取值要根据遗传交叉、变异的概率范围确定；φ（i，j）为上一小节中的相似系数。

由式（4）及式（5）可知，当φ（i，j）增大时，则种群个体的交叉概率越大，变异率则越小。进一步可知，各代种群交叉概率为：

（6）

（7）

可以看出，相比于一般算法，改进后的每代种群个体的交叉变异概率更具有针对性。

3 智慧预案下的故障线路快速定位

当电力系统中的配电网发生突发事件导致输电线路故障时，如何快速地在复杂的配电网中准确定位出故障线路的位置，就是智慧预案中对电力应急动态响应的基本要求之一。本文通过构建遗传算法在故障线路定位模型中的编码方式、开关函数以及适应度函数，来作为智慧预案下的线路故障快速定位模型，为更加准确及时地应急响应奠定重要基础。

竣工验收结算阶段也是工程造价管理当中的一个很重要的阶段，为了能够有一个可靠的造价，相关的造价单位需要按照合同中的内容条款仔细认真的进行结算。在结算之前，相关的工作人员应该仔细检测相关的资料，确保相关资料的完整性和真实性，在结算的过程中要秉承着公平公正的原则进行结算，相关的工作人员还需要对工程项目进行总结，对比工程所用的资金与造价指导书中是否相符合，将不同之处进行合理的分析。竣工验收结算阶段可以表现出造价控制管理是否有效，并且促进造价控制管理进一步的完善。

3.1 遗传编码方式

定义从系统电源到分布式电源的线路方向为正方向，若某方向上不存在分布式电源，则系统电源到负荷侧的线路方向为正方向。同时，本文利用线路上的FTU上传信息作为输入编码的主要依据，当FTU检测到的故障电流方向和定义的正方向相同时，上报信息编码为1；若FTU检测到的故障电流方向和定义的正方向相反时，上报信息编码为-1；如果没有故障电流流过，上报信息编码为0。

在改进遗传算法中，对网络内的开关和馈线进行编号，其状态信息依次作为xi（i=0，1，2，…，n）填入长度为n的染色体中。

3.2 模型开关函数

针对本文中的改进遗传算法和编码方式定义，给出算法的开关函数如下所示：

（8）

式中，I*（Sj）为第j个开关节点与馈线间的开关函数；m为其下游馈线总数；n为其上游馈线总数；xm为第j个开关下游第m条馈线的状态信息；xn为第j个开关上游第n条馈线的状态信息，处于故障状态信息值取1，处于正常状态信息值取0；K为该开关下游DG并网开关的状态信息，并网状态为1，脱网状态为0。

3.3 基于Pareto最优的多目标适应度函数

适应度函数的作用是评价染色体或粒子的优劣，在遗传算法部分，将决定哪些染色体得到复制直接保留、哪些染色体参与交叉操作的概率更大，适应度函数可以评估当前解是否是最优解或与最优解的距离。

在故障定位中，单目标适应度函数构建的原则是，在上传信息和最优解差别最小时，即最优解和实际状况最接近时，可认为达到了最优解。因此，单目标适应度函数越小，可行解离最优解越近。单目标适应度函数取：

（9）

对式（9）进行分析可知，等式右边第1项利用的是故障区段状态与实际状态的差值最小为目标函数，而第2项根据最小值原理，以故障线路最少为目标函数，直接将二者相加作为单目标适应度函数，在权值w选取不当时会影响故障的定位结果，由此导致误判或漏判。

基于以上分析，本文利用Pareto 最优概念[13-15]，能够综合全局找到多目标适应度函数下的最优解，且无需考虑权值的影响。故障区段状态与实际状态的差值指标与故障线路最少指标是一对相互制约的目标函数。介于上述两个目标之间存在矛盾关系，即无法同时达到最优解，因此需要提出合理的决策方法进行取舍。本文中的多目标适应度函数为：

（10）

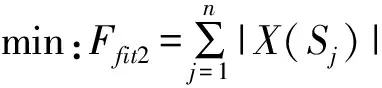
（11）

为了使求取的最优解集在Pareto前沿上分布均匀，从而保证解的多样性，设计了个体适应度距离算子。个体适应距离是目标空间上与相邻个体+1和-1之间的距离，首先初始化同层的个体距离，对同一代的个体按各个目标函数值的大小进行升序排序，设目标函数总数为M；最后，计算个体在目标函数下的两侧点的相对距离差值，即适应距离：

（12）

式中，L[i]m为第i个个体在第m个目标函数下的值，Fmaxfitm和Fminfitm分别为第m个目标函数在所有可行解集中取到的最大值和最小值。

将个体i在每个目标函数下的适应距离进行叠加，得到该个体的总体适应度：

L[i]d=L[i]1+L[i]2

（13）

通过优先选择在同一非支配层中适应距离较大的个体，使得求解结果在Pareto前沿上均匀的分布，保证了解集的多样性。

4 算例分析

本文以广州市某小型配电网络作为算例仿真对象，其简化后网络结构如图3所示。

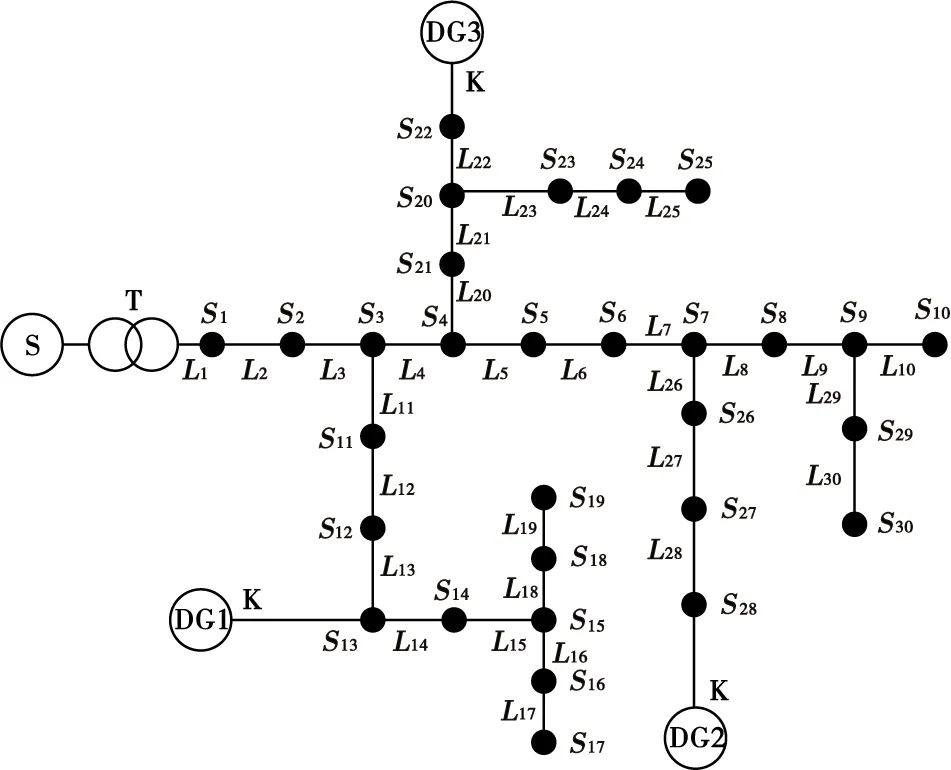
图3 网络节点拓扑Fig.3 Network node topology

图3中，DG表示分布式电源，L表示馈线，S表示开关，K表示DG并网开关。在算例中假设每个开关处都有FTU设备，电流正方向为从电源流向线路终端负荷侧。

（1）单一故障类型仿真分析。针对单一线路因突发事件导致线路故障的情景进行分析，本文分别假设3种不同的线路故障场景，仿真结果见表1。

表1 单故障类型仿真结果Tab.1 simulation results of single fault type

表1中，[K1、K2]表示DG的接入情况，1表示DG接入系统，0表示未接入系统。仿真结果曲线如图4所示。

图4 单一故障类型迭代过程Fig.4 Iterative process of single fault type

从图4中可以看出，迭代至22代左右时目标函数值取得最小，同时由表1能够看出，本文中的模型在因突发事件导致的单线路故障定位问题中，具有较好的故障线路定位准确性。

（2）多重故障类型仿真分析。针对多故障类型进行仿真发分析，同样假设3种不同的线路故障情景进行仿真，仿真结果见表2。

表2 多故障类型仿真结果Tab.2 Multi fault type simulation results

得到仿真结果曲线如图5所示。从图5中可以看出，迭代至30代左右时目标函数值取得最小，同时由表2能够看出，本文中的模型在因突发事件导致的多线路故障定位问题中，具有较好的故障线路定位准确性。

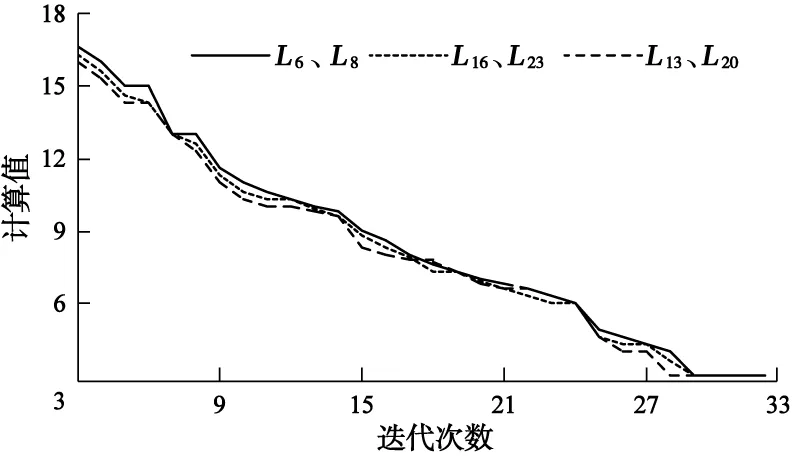
图5 多重故障类型迭代过程Fig.5 Iterative process of multiple fault types

（3）网络分区域模型对算法增益分析。由1.2节分析可知，利用APTS简化模型可以对算法维度进行一定程度的简化，具体简化程度取决于网络拓扑结构，例如若线路发生故障，则APTS简化模型能够将计算维度从30维降低至16维，缩小了14维，近似将计算维度降低一半，从而大大加快了模型计算速度。本文通过将APTS简化模型去除后的算法模型与本文模型进行算法比较，每种情景各计算50次，结果见表3。

表3 网络结构分区域对算法的增益Tab.3 Gain of network structure partition to algorithm

由表3能够看出，对因突发事件导致的线路故障定位模型中，加入APTS简化域模型后，再利用改进遗传算法进行最优解求解过程中，可以大大减少算法的迭代次数。同时，对计算时间也相应有所减少，且随着故障问题的复杂化，求解速率提升的程度也有所加大，这是因为随着模型的规模不断增大，网络无源树也相应更多，从而计算维度降低程度更大，则APTS简化模型对算法的增益不断增强。

（4）改进遗传算法对模型的增益分析。由2.2节分析可知，通过利用相似系数的改进，能够对种群个体的交叉概率和变异概率进行提高，进一步大大提高因突发事件导致的线路故障定位算法的计算速度，本模型还分析了相似系数的改进对算法的增益效果。

通过对比本文中的算法和遗传算法的运行结果，每种情况各迭代50次，结果见表4。由表4可以看出，对因突发事件导致的线路故障定位模型中，改进相似系数后，再利用遗传粒子群算法进行最优解求解过程中，能够一定程度上减少迭代次数，计算时间也相应地有所减少，从而体现出其在因突发事件导致的线路故障定位问题中的增益优势。

表4 改进遗传算法对模型的增益Tab.4 Gain of improved genetic algorithm on model

此外，本文以线路因突发事件导致的线路故障问题为例，进行不同算法的仿真过程如图6所示。对于本文中的定位模型能够在22代左右就出现最优解，而对于传统遗传算法，则在33代附近才产生最优解，通过该例就能够看出改进遗传算法在提升算法速度上具有很强的优势。

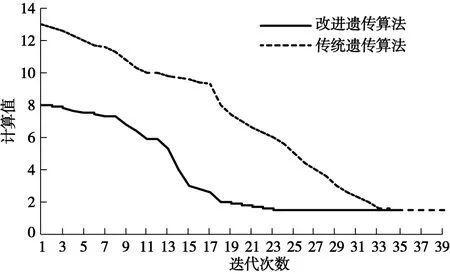
图6 不同算法迭代过程Fig.6 Iterative process of different algorithms

（5）Pareto最优对模型的增益分析。由3.1节分析可知，利用基于Pareto最优的多目标适应度函数可以有效的减少算法出现误判或漏判的情况，利用Pareto 最优概念，能够综合全局找到多目标适应度函数下的最优解，且无需考虑权值的影响。本模型还分析了构建基于Pareto最优的多目标适应度函数对算法减少误判或漏判的情况的增益效果，结果见表5，每种情况各迭代100次。

由表5可以看出，2种方法收敛次数大致相当，但基于Pareto最优的多目标适应度函数对因突发事件导致的线路故障定位方法正确率很高，而单目标优化配电网故障定位方法不能完全准确定位。因此本文算法在在单种或多种类型信息误报情形下依然能够准确定位故障区段，可靠性高。随着模型的规模不断增大，故障问题的不断复杂化，故障定位的可靠性要求也相应越高，基于Pareto最优的多目标适应度函数对因突发事件导致的线路故障定位问题具有明显的可靠性增益。

表5 Pareto最优对模型的增益Tab.5 Pareto optimal model gain

5 结论

由智慧型电力应急预案的概念可知，要实现基于事件推理机制的无脚本动态应急响应，则响应的时效性就是智慧预案的重中之重。而对于日渐复杂的配电网络，当线路因突发事件导致故障时，则智慧预案应该能够快速准确地定位出故障线路的位置，从而为动态应急响应做好准备。本文首先利用APTS简化模型对复杂配电网进行简化，通过去掉无故障线路的无源树网络，能够减小运算维度，加快运算速度，从而提升智慧预案的时效性；此外，改进的遗传算法模型和多目标适应度函数的构建，在进一步提升算法速度的同时，还使得因突发事件导致的线路故障模型具有很好的容错性能，从而极大地提高了模型的准确性。综上可知，智慧预案下的故障线路定位模型具有极强的时效性和准确性。