基于弹性理论设计边坡防护方法研究

徐 立，刘 晗，吕俊秀，干 钢

（浙江大学建筑设计研究院有限公司，浙江 杭州 310000）

岩土体都处于天然应力场[1-2]中，天然应力场包括垂直应力和水平应力2部分，垂直应力主要是自重应力，可根据经典土力学理论计算；而水平应力影响因素较多，一般难以准确计算，大多通过试验进行量测。此外，土体是三相体，受力后变形不同于理想弹性材料，但纵观整个土力学发展历程及近年来大量工程实践经验，将弹性理论运用于土力学计算，并指导设计，误差满足工程要求。为便于计算，在讨论相关问题时，不考虑天然土体中水平应力，并将土体简化为理想弹性材料。在岩土体中开挖边坡，原土体状态将会改变，且应力场将重新分布，称作为卸荷作态[3]。卸荷状态会在边坡中形成卸荷影响带，这个影响带有一定范围，超过这一范围后，土体的应力状态可认为和原来状态相同。如果能知道原状态中各个方向应力分布情况，然后在设计边坡开挖线上施加一个作用力，这个作用力对边坡线产生的效应与边坡将要挖除的那一部分土体对边坡线施加的作用效应相一致，那么，对于理想弹性材料[4-8]而言，这个状态是等效的。

应该指出，土是三相体，不同于理想弹性材料，他具有特殊性，如土体卸荷再压缩时，表现出的性质与原状土压缩时的性质有所不同，因此直接将原状土内的应力状态用开挖后的边坡加某一外荷载来等效，理论上不严密。但由此引出的开挖影响范围概念是正确的，若考虑一定安全系数，采用这种方法进行设计可行。以西南山区某高填方边坡为例，在对地质概况进行了详细调查的基础上，对边坡在不同工况下的稳定性进行计算评价研究。

1 开挖影响区概念和计算

1.1 开挖影响区概念

边坡开挖后坡体内部应力和变形变化情况如图1、图2所示。由图2可知，距坡面距离增大，边坡坡体内部应力及变形均逐渐趋于稳定。应力趋于原始坡体的应力，而变形则逐步缩小，直至可以忽略。这表明，由于边坡开挖，坡体内部的应力及变形在某一范围内影响较大，这一影响范围称为开挖影响区。工程经验表明，坡体失稳是由于坡体内部发生了较大的位移和变形造成的。边坡开挖影响区内，坡体应力重分布和变形显著，是失稳破坏的主要区域。

图1 应力作用范围Fig.1 Stress range

图2 应力形变范围Fig.2 Stress deformation range

1.2 开挖影响区计算

理论上，边坡开挖影响区应通过弹性力学方法，分析边坡坡体内部各点位移情况，作出位移曲线图，由曲线图进行计算。但这样分析计算稍显复杂，有的学者通过敏感性分析，提出相应计算公式，并完成了相应的工程验证。设开挖影响区宽度为B，开挖高度为H，开挖角度为β，开挖台阶宽度为b，边坡岩土体内摩擦角为φ，岩土体重度为γ，开挖影响系数为α，则开挖影响区范围见式（1）。

（1）

2 边坡弹性应力计算及应用

2.1 边坡坡体内部弹性应力计算

边坡内部应力状态可采用弹性理论中楔形体应力分布情况进行模拟计算，如图3所示。

图3 边坡顶面水平时边坡内部应力计算Fig.3 Calculation of the internal stress of the slope when the top surface of the slope is horizontal

设边坡岩土体密度ρ，根据弹性理论，当边顶面水平时，在自重作用下边坡内部应力用式（2）计算。

（2）

如果角度在x轴左边，则以负值代入。边坡内部应力分布如图4所示，在进行边坡应力分析及边坡设计时，希望得到沿坡面BC法线及沿坡面方向的应力分布。但式（2）是通过极坐标计算，为应用方便，需将计算结果加以转化。

图4 边坡内部应力分布Fig.4 Internal stress distribution of slope

鉴于篇幅，本文仅列出转化结果，建立not坐标系，n方向为边坡坡面法线方向，t方向为边坡坡面方向，边坡倾角为β，如图5所示。

图5 边坡应力坐标转化Fig.5 Slope stress coordinate conversion

经推导，得到边坡法向及切向应力，见式（3）。

（3）

2.2 边坡弹性应力计算结果应用

对于理想弹性材料，材料在某一瞬时应变完全取决于该瞬时材料所受外力（温度不考虑），而与加载历史、加载顺序无关。但岩土体不属于理想弹性体，弹性理论应用于岩土体时应加以修正。岩土材料回弹—再压缩曲线如图6所示。岩土材料再压缩过程与压缩过程是不同的，只有经历过卸载点b后，再压缩曲线与压缩曲线相同。

图6 土的回弹—再压缩曲线Fig.6 Soil rebound-recompression curve

为了解岩土体与理想弹性材料之间区别，建立如下模型：假设在边坡上施加一荷载，该荷载使坡体内部岩土体加载后的状态与未开挖时坡体内部（边坡线以内）的状态一致。图6中，令其对应于b点，然后卸载，卸载过程中，岩土体将产生膨胀，对应于回弹曲线，即图6中bc段；卸载完成后，岩土体处于c点所对应的状态，实际上这个过程就是开挖影响区形成的过程。显然，要回到b点状态，就要对岩土体进行再压缩，如果能获得b点及c点岩土相应压缩参数，便可计算出从c点到b点所需施加的外荷载，也就是边坡防护所需提供的抗力。从理论上讲，上述分析的方法是相对严密的，但要想获得2个状态的物理参数，然后进行计算和设计，运用上很不方便。为使应用方便，采用简化计算方法，即假定解除应力和防护提供的应力一致时，边坡内部经过应力调整，将重新恢复到原来状态，同时考虑原边坡所处状态各有不同，在此基础上考虑一定安全系数，即采用式（4）的防护设计。

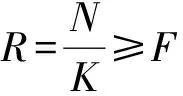
（4）

式中，R为边坡设计防护能力；N为边坡计算防护能力；K为安全系数；F为边坡坡面弹性作用力。

在进行边坡防护设计时，可按式（4）计算防护能力，进而选用相应的防护形式。当然，防护的抗力提供部分应位于边坡开挖影响范围以下一定距离。在实际计算中，可利用式（1）确定相应影响区范围，而抗力提供部分（锚固部分）起算位置则位于影响区下方1.5～2.0 m处。

2.3 应用条件

应用边坡内部弹性应力进行边坡设计时，由于计算公式是在一定假定前提下推导的，公式的应用有一定限制，有关应用条件如下。

（1）边坡构成材料相对均匀，在一定厚度范围内，材料变化不大。计算边坡坡体内部岩土体组成结构单一，如全土质边坡、全岩质边坡。实际上，任何边坡岩土体都是在漫长的沉积而成的，经过各种地质作用，形成不同的土岩组合，在一定尺度范围内组成边坡的土质类别单一，可利用上述理论。对于土岩组合边坡、软硬岩互层以及其他存在明显结构面的边坡而言，滑动位置一般都是沿结构面软弱位置，其边坡防护设计也是明确的，无需复杂的计算。

（2）边坡顶面水平。实际上，这个应用条件仅针对式（2）是在坡顶面水平情况下导出。对于边坡坡顶面为倾斜时，如图7所示。

图7 边坡坡面倾斜时弹性应力计算Fig.7 Calculation of elastic stress when slope is inclined

相应计算公式要进行调整，可按式（5）计算：

（5）

式中，A、B、C、D为系数，计算相对复杂，与岩土体的密度ρ、倾角β和α的值有关，但可编制成相关计算表格进行计算，见表1。

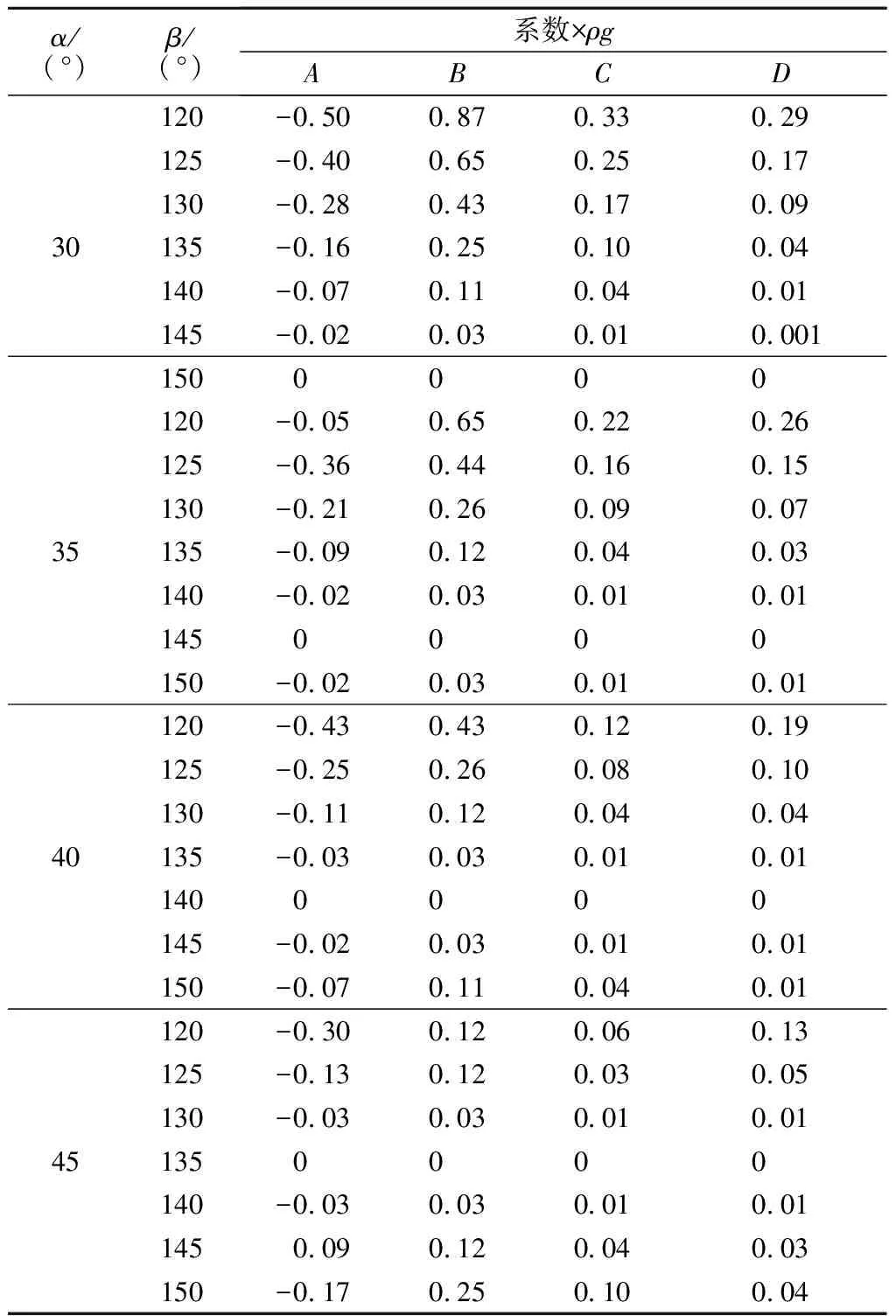
表1 弹性应力计算系数Tab.1 Elastic stress calculation coefficient

3 边坡稳定性分析

3.1 计算模型

根据工程地质资料，选择3个典型剖面作为边坡稳定性分析的计算剖面，平面位置如图8所示。

3.2 计算参数及工况

（1）计算参数。计算参数的选取主要依据现场及详勘报告，并结合当地工程经验值而综合确定。抗剪强度指标采用直接剪切指标，具体见表2。

（2）计算工况。根据项目场地的工程地质条件，考虑当地气候条件，边坡稳定性分析采用3种工况进行计算，分别为天然工况、暴雨工况和暴雨+地震工况。对于地震作用，根据 GB 18306—2015《中国地震动参数区划图》，项目场地抗震设防烈度为7度，设计基本地震加速度值为0.10g。同时，考虑场地内人群荷载、车辆荷载、建筑物等荷载作用，在边坡稳定性计算中假定坡顶范围内存在180 kPa的分布荷载。

图8 设计计算模型Fig.8 Design calculation model

表2 岩土参数建议值Tab.2 Recommended geotechnical parameters

3.3 结果分析

结合弹性理论分析边坡基于不同工况下的稳定性[9-10]，获得边坡稳定安全系数见表3。

表3 边坡稳定安全系数结果比较Tab.3 Comparison of results

以1-1剖面为例，边坡在不同工况下的最危险滑动面如图9所示。

图9 1-1剖面不同工况下最危险滑动面Fig.9 The most dangerous sliding surface of 1-1 section under different working conditions

根据GB 51254—2017《高填方地基技术规范》要求，填筑边坡在天然工况、暴雨工况和暴雨+地震工况下的稳定计算安全系数，应分别不小于1.30、1.15、1.05。通过分析可知，3个典型剖面在3种工况下的安全系数均满足规范要求的稳定安全系数值。在3种计算工况下，边坡最危险滑动面均穿过填土层，属于深层滑动，说明采用土工格栅加筋处理后，有效减少了边坡坡面发生局部破坏的可能性，在一定程度上提高了边坡整体稳定性。

3.4 边坡变形监测结果分析

填方边坡施工完成后，在边坡坡面布置4 个变形监测断面，共计14个变形监测点。经分析，各监测点反映的规律类似，因此，以B1J02号监测点为例，对边坡坡面水平位移和竖向位移变化情况进行分析说明。监测点位移变化曲线如图10所示，位移变化速率曲线如图11所示。

图10 B1J02 监测点位移变化曲线Fig.10 Displacement curve of monitoring point B1J02

由图10、图11可知，填方边坡最大累计水平位移量为37.3 mm，水平位移变化速率为0.03 mm/d；最大累计垂直位移量为43.0 mm，垂直位移变化速率为-0.04 mm/d。即边坡施工完成后，随着时间的延长，B1J02号监测点水平及竖向变形减缓并逐渐收敛，说明填方边坡变形已趋于稳定，边坡整体稳定性良好。

图11 B1J02 监测点位移变化速率曲线Fig.11 Displacement change rate curve of monitoring point B1J02

4 结语

边坡工程是岩土工程中一个重要分支，几乎所有岩土工程都要涉及到岩土边坡开挖、防护。本文将弹性理论的相关解答引入到边坡工程中，旨在为边坡防护设计提供一种新的思路。应该指明，采用此种方法进行边坡防护设计，目前应用得还不多，从工程安全的角度出发，设计人员可采用此种方法设计，并与传统设计方法类比，积累经验以供参考。高填方边坡工程技术难度大，边坡稳定性对工程建设的安全具有较大的影响，在设计施工时应引起足够重视。