基于海洋捕食者算法的武器目标分配问题研究

张 青，曾庆华，张宗宇，叶宵宇

(中山大学 航空航天学院， 广东 深圳 518107)

1 引言

求解武器-目标分配优化问题是空战决策的重要内容，也是决定能否达成作战效益的重要因素[1]。目前围绕该问题的解决方法主要包括传统的分支定界、动态规划与合同法等，以及智能优化算法，如遗传算法、模拟退火算法、蚁群及粒子群算法等[2]。传统分配方法虽然理论基础较简单，但求解时间长、效率低，难以满足分配的实时性要求且难以处理多维目标分配问题。而智能优化算法虽然在解决上述问题方面有所突破，但也存在一定局限性，如容易早熟收敛，陷入局部最优，收敛速度慢等[3]。

围绕上述问题，近年来越来越多的学者青睐采用基于生物特性启发的新颖智能算法来解决上述问题[4]。Jun Wang等[5]从非线性整数规划角度出发，结合局部搜索算法，提出了一种混合离散灰狼优化算法，极大地提升了大规模分配问题的可扩展性。Rafet Durgut等[6]受蜜蜂智能行为启发，构建了求解目标分配问题的人工蜂群算法，取得了良好的分配效果。You li等[7]构建了双目标武器-分配模型，使用帕累托蚁群优化算法，提出改进的运动概率规则来缓解早熟收敛，有效提升了传统蚁群算法的性能。Yao jishuai等[8]通过改进帝王蝶优化算法，使用贪心策略迁移操作和自适应交叉算子解决了收敛速度和精度低的问题。

上述研究能够不同程度地提高算法的全局寻优能力和收敛速度，但仍存在收敛精度不高、对不同复杂函数鲁棒性较差和难以跳出局部最优的现象。为提高武器-目标分配问题的求解效率和提高求解质量，本文给出了一种基于改进的海洋捕食者算法的求解策略。

2 武器-目标分配问题建模

2.1 目标分配问题描述

目标分配属于典型的规划问题，通过对战场环境、给定资源以及各种约束条件的分析计算，对任务目标进行合理规划分配，以达到最佳作战效果[9]。由图1可见敌我双方作战场景。图中黄色区域为我方阵营，武器配置为m枚导弹。红色区域为敌方阵营，具有n个目标。我方的任务为最大程度地摧毁敌方目标，因此，需要在考虑作战意图、武器性能、目标价值等因素的基础上，以摧毁效益最大值为目标函数，建立武器-目标分配模型。

图1 敌我双方作战场景示意图Fig.1 Distribution Diagram

首先，在此场景中，我方武器m枚，敌方目标n个。xij为分配状态，确定其分配矩阵X：

(1)

该矩阵中，第i行代表第i个武器，第j列代表第j个目标。xij为布尔值，代表分配状态。当xij=1时，意为第i个武器被分配打击第j个目标，当xij=0时，代表未分配第i个武器打击第j个目标。

2.2 目标函数及假设约束

目标函数通常由作战任务与指挥决策的侧重点决定，我方作战意图为最大程度地摧毁敌方目标，因此，以摧毁效益为目标函数。同时考虑武器性能、目标价值、武器成本、摧毁概率等因素，摧毁效益Λ可表达为摧毁收益Α减去打击成本g：

(2)

因此设定摧毁效益最大值为目标函数：

(3)

对求解问题进行如下假设：不考虑武器发射的时间顺序以及过程中的突发情况；不同武器与不同目标之间的打击结果相互独立，互不干扰；武器数量大于目标数量，一枚武器只能打击一个目标，但一个目标可被多枚武器攻击。

此外，模型需满足式(4)约束条件，该约束表示一个目标至少会被分配到一个武器，最多会被分配到uj个武器；一个武器只能分配给一个目标。

(4)

3 改进的海洋捕食者算法

海洋捕食者算法(marine predator algorithm，MPA)是Faramarzi于2020年提出的一种新颖的群智能算法，该算法受海洋捕食者与猎物之间的行为特性启发而提出[10]。并在COVID-19感染人数的预测[11]、光伏模型参数优化[12]等领域得到广泛应用。

3.1 基本的海洋捕食者算法原理及步骤

海洋捕食者算法主要灵感来源于海洋捕食者的觅食策略—莱维运动与布朗运动，以及捕食者和猎物之间相互作用的最佳遭遇策略。捕食者意为最优解，猎物意为当前解，核心步骤在于猎物位置不断地更新变化，同时其适应度值与捕食者的适应度值相比较，若优于捕食者，则此猎物将被捕食者“捕捉”，捕食者位置将会进行更新[10]。算法中的猎物位置根据其与捕食者的相对关系而改变，此外，还会根据环境而改变，例如因涡流形成或鱼类聚集装置(FAD)效应而使猎物长时间聚集在FAD附近的现象被视为局部最优解。若要摆脱当前局部最优解，则需要一个长跳跃操作。

3.2 改进的基于反向学习策略的种群初始化

海洋捕食者算法作为元启发式算法，是一种基于种群的方法。原始算法中种群初始解随机均匀分布在搜索空间上：

X0=Xmin+rand(Xmax-Xmin)

(5)

其中，Xmax与Xmin分别代表解变量的上下限，rand是0～1的均匀随机向量。

优化算法计算时间与初始种群中个体和最优个体间的距离有关，若初始种群靠近最优解附近，则种群所有个体会快速收敛。然而随机生成的初始种群收敛速度不可估计，若在初始解中考虑反向种群，那么个体与反向个体更靠近最优个体的概率是50%，选中更靠近最优个体的个体作为初始种群，会加快算法收敛速度，因此初始种群前一半采用式(5)生成，另一半基于式(5)采用式(6)生成，其数学表达如式(6)：

(6)

在算法初期建立2个矩阵，分别为捕食者矩阵E(E∈Rs×d)与猎物矩阵P(P∈Rs×d)，依次储存最优解与当前解。当种群初始化时，捕食者矩阵与猎物矩阵都储存着初始种群，随着猎物位置(当前解)的不断更新，捕食者位置(最优解)也会随着之更新。

3.3 基于自适应参数轮盘赌的猎物更新方式

MPA优化过程主要模拟海洋中捕食者与猎物之间的捕食过程，根据捕食者与猎物之间的速度比，可将整个迭代过程分为3个更新阶段：

第一阶段(迭代前期)：当猎物运动速度很快时，即高速比情况下，猎物采取布朗运动，捕食者最佳策略是静止不动，对应的数学模型为：

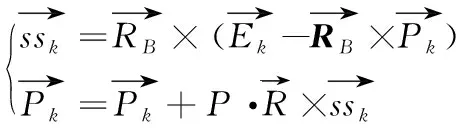
(7)

第二阶段(迭代中期)：当猎物运动速度与捕食者运动速度相当，即速度比接近1时，此时由全局搜索逐渐转化为局部搜索，在这个阶段，全局与局部搜索能力都很重要。因此对一半猎物注重其探索能力，对另一半猎物则注重开发能力(即局部搜索能力)。其数学模型为：

(8)

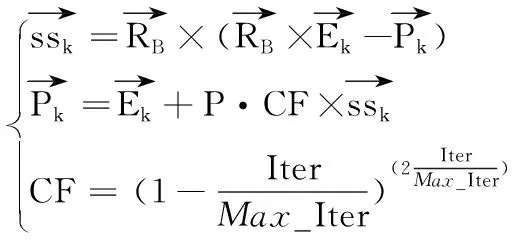
(9)

原始算法机械地规定前一半种群注重开发能力，后一半种群注重探索能力，这样势必导致算法全局搜索能力和局部搜索能力之间的不平衡。而本文采用基于自适应参数轮盘赌的更新方式，能够增强种群变化的随机性。具体而言，即自主生成探索与开发能力在轮盘上的占比如式(10)：

(10)

其中，w为自适应参数，fitn为当前解的适应度值，fitw为上一代的最差的适应度值,fitb为上一代最优的适应度值。

式(10)表明：当w<0.5时，此时当前解适应度值落在靠左处，需要较大的步长跳出局部最优，需要增强全局搜索能力；当w>0.5时，此时当前解适应度值落在靠右处，靠近最优值，只需要较小的步长继续局部搜索。轮盘赌中探索与开发占比如图2所示，轮盘赌法可以生成0～1的随机数r，当r

图2 轮盘赌中探索与开发占比示意图Fig.2 Roulette diagram

第三阶段(迭代后期)：当猎物速度很慢，即低速比时，捕食者的最佳策略是采取莱维运动，其数学表示为：

(11)

3.4 算法步骤

改进的海洋捕食者算法((improved marine predator algorithms，IMPA)实现步骤如图3所示。

图3 算法流程框图Fig.3 Algorithm flow chart

步骤1：参数设定。设置种群数量，解的维数，最大迭代次数，FADs等；

步骤2：目标函数的确定。通过式(3)来求解每个猎物的适应度值，从而达到筛选的过程；

步骤3：种群初始化。通过反向学习的方式来确定初始种群，增加收敛速度；

步骤4：形成初始猎物矩阵后，计算每个猎物的适应度值并进行排序替换，形成捕食者矩阵；

步骤5：猎物更新。在迭代不同时期采用不同的更新方式(迭代前1/3时，猎物采取布朗运动；在迭代中期，即1/3～2/3时，通过自适应参数轮盘赌法来确定采用莱维运动还是布朗运动；在迭代后1/3时，捕食者采用的策略是莱维运动。)

步骤6：猎物更新后，重新计算每个猎物的适应度值，同样对适应度值进行排序替换，形成捕食者猎物，并进行海洋记忆储存；

步骤7：考虑涡流形成与FAD效应：在迭代完成后，为脱离局部最优解，通过FAD效应进一步改变猎物的位置，计算其适应度值，并对捕食者矩阵进行更新；

步骤8：判断算法当前迭代次数Iter是否达到最大迭代次数Max_Iter，若满足则终止算法；输出最佳适应度值与最佳解，若不满足，则转至步骤5。

4 仿真校验

4.1 任务描述及参数设定

本小节通过数值仿真手段对所提算法有效性进行验证，给定敌我双方的作战场景如下，我方无人机侦察到敌方8个目标，派遣我方10枚导弹攻击敌方目标。假设我方有两种武器，并且武器对目标的摧毁概率只与武器类别有关。此外，目标具有一定的防御系统，决定了击落武器的概率。基于以上假设，设定模型参数与算法参数，如表1所示。

表1 模型参数及算法参数Table 1 Model parameters and algorithm parameters

4.2 仿真验证

为了验证海洋捕食者算法及改进后的海洋捕食者算法性能，将其与经典的启发式智能算法与新颖的智能算法进行对比。取海洋捕食者算法、遗传算法[13](genetic algorithms，GA)、粒子群算法(particle swarm optimization，PSO)以及蜻蜓优化算法[14](dragonfly algorithm，DA)与鲸鱼优化算法[15](whale optimization algorithm，WOA)作为对比算法。为避免智能算法的随机性对结果造成的误差，将各类算法独立运行100次进行分析。表2给出了各个算法解算得到的100组适应度值中最大值、最小值、平均值、单次运行时间、100次总运行时间、所计算适应度值的方差与未算出解的次数等统计数据。

表2 不同算法求解结果Table 2 Comparison table of solution results of different algorithms

为了更直观地显示IMPA的寻优效果，图4为6种算法解算此模型的箱线图。由图可知，IMPA所解算出的适应度值中最大值、最小值都大于其余算法。其次，IMPA的箱体最窄，说明IMPA的100组数据波动程度最小，最稳定。PSO算法最大值与IMPA算法一致，但PSO算法箱体最长，其算法稳定性较差。因此，IMPA在适应度平均水平以及波动程度等方面于6种算法中表现最优。

图4 算法性能箱线图Fig.4 Comparison diagram of algorithm performance

图5为6种算法适应度值统计曲线，首先，由整体图5可知，重复进行100次的实验，只有MPA与IMPA算法每次都解算出了解，而其余4种算法皆出现了未解算出解的情况。因此MPA与IMPA的求解能力高于其余4种算法。其次，MPA与IMPA解算出的适应度值波动程度整体优于其余4种算法，而粒子群算法波动最大，通过局部放大图可知，MPA与IMPA数据波动程度接近，但从表2的方差来看，MPA的方差为0.002 0，IMPA的方差为0.001 6，IMPA的稳定程度要优于MPA。

图5 适应度值曲线Fig.5 Comparison of the degree of data fluctuation

图6给出重复100次实验中MPA与IMPA算法解算出的最优值的迭代过程，MPA解算出的最优适应度值为1.873 3，IMPA解算出最优适应度值为1.885 3。将其迭代过程进行对比，MPA于120代左右收敛到最优值，而IMPA于20代左右就收敛到最优值。可知，IMPA的收敛速度高于MPA。

图6 MPA与IMPA适应度值迭代过程曲线Fig.6 Iterative process of MPA and IMPA fitness values

以上内容主要针对不同算法求解目标函数的适应度值进行了最值和方差分析，另外对算法的求解时间与求解能力进行分析。由于在目标函数中引入了惩罚因子，可能会出现无解的情况。通过表2可知，MPA以及IMPA得出解的概率为100%，GA算法为97%、PSO算法为73%、DA算法为72%、 WOA算法为54%，因此海洋捕食者算法有很强的求解能力。此外，通过事后统计法对算法的时间复杂度进行分析，由运行时间来看，MPA、IMPA、WOA，处于第一梯队，PSO处于第二梯队、GA处于第三梯队，DA运行时间最长，处于第四梯队。同时在时间相近的情况下，MPA、IMPA、WOA三者中IMPA的适应度值最大，得出的解最优。因此，用IMPA算法得出的最优适应度值对应的分配方案为最佳分配方案，其方案为表3。

表3给出了最优的分配方案及摧毁收益的具体数值，第一行表明了导弹的数量与序号，第二行给出导弹序号所对应的打击目标序号。在此分配方案中，有3枚导弹对目标5进行攻击，而通过表1可知，目标5的价值度最高，因此将较多火力集中在价值度高的目标上，获得最大的收益。通过表2可知，IMPA能够解算出最优的适应度值，因此最大适应度值对应的分配方案最优。

表3 最佳分配方案Table 3 Optimal allocation scheme

5 结论

1) 将海洋捕食者算法应用于武器-目标分配问题，很好地解决了其余算法易陷入局部最优解的问题；

2) 通过反向学习策略对海洋捕食者算法种群初始化的改进，增加了算法的收敛速度；通过自适应参数轮盘赌法对猎物更新方式的改进，增加了种群更新的随机性，以及平衡了算法全局与局部搜索能力。