一元微积分中函数极限的求解方法
◎刘 燕
(克拉玛依职业技术学院基础部,新疆 克拉玛依 834000)
一、引 言
在高职高专的高等数学上册中,一元微积分是由函数、极限与连续、导数与微分、微分学的应用、不定积分、定积分及其应用、微分方程七个教学模块构成,其中连续、导数和定积分是微积分中非常重要的三个数学概念,而这三个数学概念都是用极限刻画的,因此,熟练掌握极限的求解方法对学好一元微积分是至关重要的.
二、函数极限的求解方法
1.利用观察法求极限(观察型)
在极限概念的章节中,有许多节要求观察在自变量的某种变化过程中函数的变化趋势.这种类型的题目就是典型的利用观察法求极限,它的求解方法是先作图或列表,然后观察当自变量在指定的变化过程中函数的变化趋势.

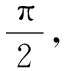

图1
2.利用无穷小的性质求极限(无穷小型)
无穷小的性质有三条:
(1)有限个无穷小的代数和仍为无穷小;
(2)有限个无穷小的乘积仍为无穷小;
(3)有界函数与无穷小的乘积仍为无穷小.
当遇到无穷小量相加、相减、相乘时,一般情况下可以判定此时极限为无穷小型,我们常常利用无穷小的性质求极限.针对性质(3)要牢记,常见的有界函数有七个,它们分别是常数、正弦、余弦、反正弦、反余弦,反正切和反余切,只要函数中含有有界函数,就要认真分析剩余的部分是否无穷小.
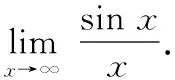

3.利用无穷小与无穷大的关系求极限(无穷大型)
通过分析发现,函数在极限条件下是无穷大时,可以判断该极限属于无穷大型,可以利用无穷大与无穷小在同一条件下互倒的关系解题.
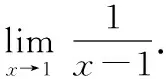
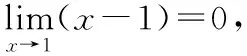
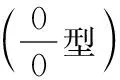
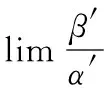
该定理表明,在计算两个无穷小之比的极限时,可将分子或分母的乘积因子代换为与其等价的无穷小量,进而简化极限求解的计算过程.

当→0时,sin~,ln(1+)~,




=1.
注意:在利用等价无穷小代换定理时,对于代数运算中各无穷小不能分别替换,必须整体代换.
5.利用极限运算法则求极限(公式型)
通过分析发现,只要符合极限的四则运算法则的条件都可以利用法则解题.
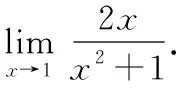
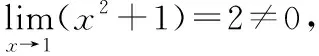
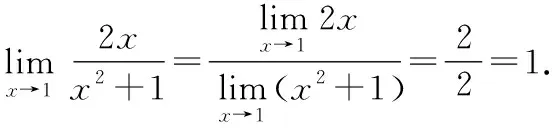
6求下列极限:
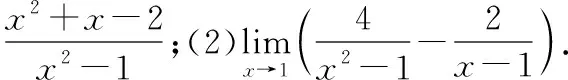
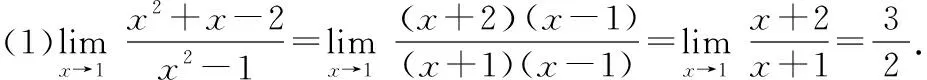
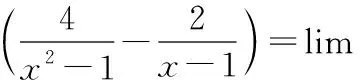
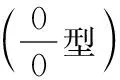
通过分析发现,分子、分母在某种极限条件下极限都为0,且分子或者分母含有根式函数,这时常常利用平方差公式对分子或分母进行有理化,从而求解极限.
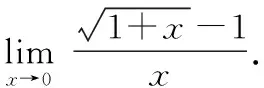
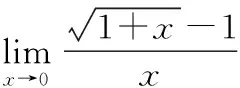
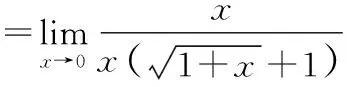


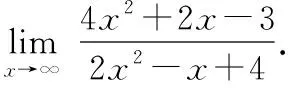
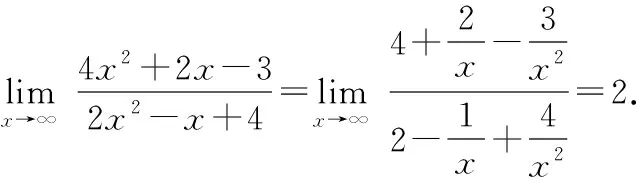
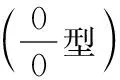
有些极限用一般的方法无法求解,但借助变量代换法求极限却能顺利解决.
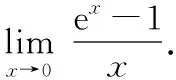
设e-1=,则=ln(+1),当→0时有→0,故
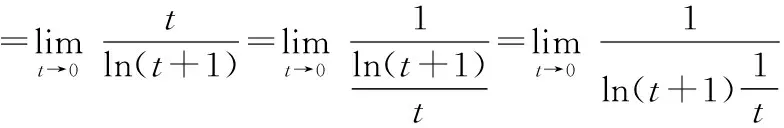

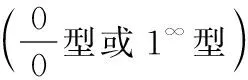
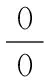
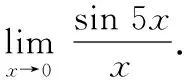



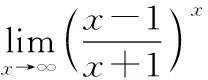
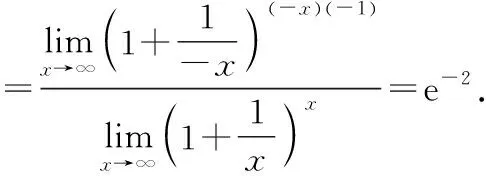
夹逼准则又称两边夹准则.在极限求解过程中,常常把函数或数列通过放大和缩小,使两边的新函数或新数列极限相同,进而利用夹逼准则求原函数或原数列的极限.

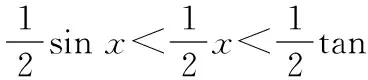

图2
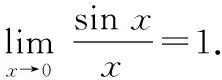
12.利用函数的连续性求极限(代入型)
由于初等函数在其定义域内都是连续的,所以求极限时我们常常观察一下函数是否在该点有定义,若有,即可利用函数的连续性求极限,若无,改用其他方法.
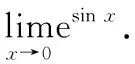
因为函数()=esin 是初等函数,并且它在=0处有定义且连续,
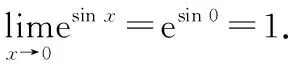
13.利用导数的定义求极限(凑导型)
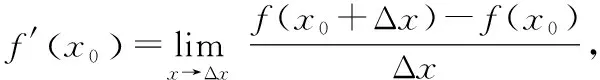
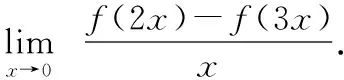
∵′(0)=1,
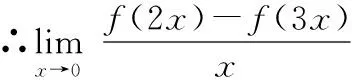
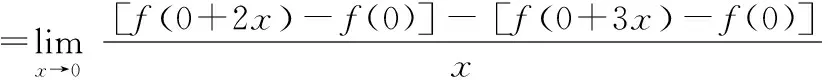

=2′(0)-3′(0)=-1.
14.利用L′hospital法则求极限(未定型)
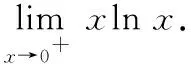
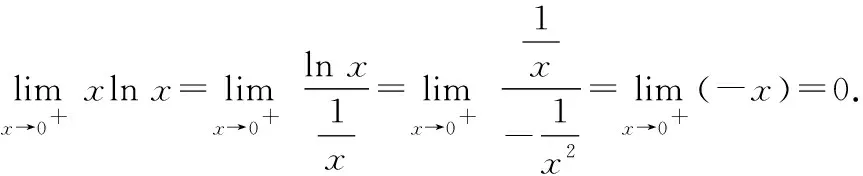
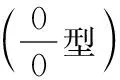
有些极限可以通过巧妙地构建函数,使其在某区间上符合Lagrange中值定理的条件,从而利用Lagrange中值定理求极限.

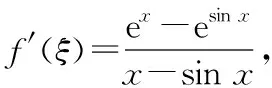
三、结束语
在高职高专教材中,一般情况下有这十五种求极限的方法,在极限求解计算中到底运用哪一种方法,还需要具体问题具体分析,请读者在计算中认真分析,找准类型,灵活运用求极限方法.一个求极限的题目,有时所用到的方法也不止一个,大家在能够融会贯通的情况下,选择出适当的方法,这样不仅准确率高,而且会省去许多不必要的麻烦,起到事半功倍的效果.

