区域经济研究中夜间灯光与GDP的相关性特征

肖巧俐，王跃，2

(1.华东理工大学 商学院，上海 200237；2.华东理工大学 体育科学与工程学院，上海 200237)

0 引言

一直以来，中国官方GDP统计数据的真实性被部分学者质疑，主要的观点是认为中国存在夸大GDP数据的可能性[1]。作为衡量经济发展的变量，统计数据确有一些客观存在的缺点，如由于统计方法和市场不完善造成的数据质量不高，虽然可以通过添加代理变量或工具变量来解决部分问题，但这往往不能充分反映变量对研究对象的实际影响。因此，利用更客观的变量，从新的角度对经济发展水平进行衡量成为经济研究的热点。

美国国家海洋和大气管理局发布的全球夜间灯光数据近年来受到学界的关注。该数据是由美国空军气象卫星从外太空所观察到的地球不同地区的灯光亮度。夜间灯光作为一种独特的地表景观现象，代表着人类在地球表层的活动规律，其分布以及强度信息与人类社会经济发展密切相关。随着技术的进步和夜间灯光数据资源的丰富，目前夜间灯光数据已被广泛应用在全球和区域尺度的经济问题研究(如经济发展[2-4])和社会问题研究(如城市扩张[5-7]、人类活动[8]、电力能源消耗[9-10])中。

把夜间灯光作为经济社会参量的研究，主要是基于夜间灯光与经济的相关性前提，用夜间灯光作为GDP等经济指标的替代变量，而且该数据不受物价水平的影响，尤其适用于观察较长时间内不同地区的经济活动。但无论是在国家、超国家或次国家层面，使用灯光数据作为GDP代理变量时，都应该考虑替代的特征和效率，根据二者的相关性特征，提升研究设计的层次，从而提高度量国家或地区经济绩效的准确性。而目前这种替代效率，或者相关性特征的研究还有待深入。本研究以验证夜间灯光表征经济的特征和效率为目的，使用1992—2013年中国省级行政区的夜间灯光数据和GDP数据探索夜间灯光与GDP的相关关系。基于Henderson等[11]的基本回归方程，从多个视角分别审视夜间灯光数据对GDP数据的回归结果，并基于其相关性特征形成了纳入初始条件的关系方程。

Imhoff等[12]、Elvidge等[13]提出夜间灯光有望用于全球范围内的生产力、人口、能源等参数的评估，随后，有研究认为夜间灯光是比GDP本身更准确的经济活动指标，引起了大量使用灯光数据研究经济问题的现象[14]。特别地，文献[11]利用灯光数据、GDP数据、人口密度数据等建立收入增长预测模型，开发了一个新的统计框架，为统计机构效率非常低的国家提供了修正的经济增长估计方法，这一框架的适用性在其他学者的研究中也得到了检验[15]。随后，Chen等[16]使用不同种类的夜间灯光建立回归模型，发现夜间灯光能提供对产出和人口的估计，也有可能通过组合不同的灯光产品来产生综合指数，从而为相关指标产生更好的代理。这些研究成果在夜间灯光的经济问题研究上具有划时代的意义，也奠定了后续相关研究的基石。

在大量利用夜间灯光研究经济问题的文献中，研究的内容主要涉及三类。第一类是针对GDP统计数据质量不高的发展中国家和不发达国家，用夜间灯光作为经济的替代变量，如李德仁等[17]、黄亮雄等[18]用夜间灯光度量一带一路沿线国家的经济状况，Lee[19]用夜间灯光度量朝鲜的经济活动。第二类是利用夜间灯光明确的地理空间属性进行区域经济问题研究，如Elliott等[20]证明了夜间灯光可以为重大事件或自然灾害引起的社会经济变动做出反应，赫胜彬等[21]利用灯光指数来构建区域发展指数，刘华军等[22]利用夜间稳定灯光数据对中国城市经济发展的空间差异和溢出效应进行实证考察。第三类是利用夜间灯光数据重估GDP，或者改进GDP的研究，如王琪等[23]采用回归分析的方法建立了夜间灯光对GDP 的空间化模型，其回归拟合精度达到0.964，Xi等[24]运用夜间灯光数据和GDP数据，建立线性回归模型，对夜间光进行了经济建模和评价，李宗光等[25]利用夜间灯光数据估算特困区GDP，县级尺度的估算精度达到87.38%。

从这些结论可以看出，夜间灯光数据不仅是经济增长时间、空间层面的有效代理变量，更有助于理解区域经济增长空间模式的本质及异质性。总地来看，夜间灯光数据丰富了经济变量的替代指标，拓展了经济社会问题的研究方法，开辟了相关问题的研究领域。本文认为，对夜间灯光和GDP相关性的深入研究，还能进一步为提升夜间灯光在经济问题中的研究效率发挥作用，能挖掘出夜间灯光在经济问题研究中更大的能力。

1 数据与方法

20世纪美国国防气象卫星计划(defense meteorological sate-lite program，DMSP)搭载发射的可见光成像线性扫描业务系统(operational linescan system，OLS)传感器提供了全球最长时间序列(1992—2013)夜间灯光数据(简称DMSP/OLS)。本文借鉴对灯光数据进行不变目标区域法校正的论文[26-27]，对中国34个省级行政区1992—2013年的DMSP/OLS稳定灯光数据进行了相互较正、饱和矫正以及连续性矫正，计算出各区域历年的夜间灯光均值。

校正前后2013年的各地区夜间灯光均值对比如图1所示。结合实际数据发现，校正后的夜间灯光DN均值高于校正前的DN均值，对于北京、天津、上海、广东、香港、澳门、台湾等地区，校正后的DN均值远大于校正前。这是因为校正前单个像元的DN值介于0到63之间，校正的过程消除了中心区域饱和的问题，DN值介于0到171之间，更能反映经济发达地区与不发达地区的灯光差距。同时，观察地区的数据发现，校正后的夜间灯光数据更具有连续性，说明该校正方法有效修正了夜间灯光数据本身存在的误差。

本文的GDP数据为中国34个省级行政区1992—2013年的名义GDP数据，来源于国家统计局和《新中国60年统计资料汇编》，各变量的描述性统计见表1。

表1 变量描述性统计

关于夜间灯光与GDP的基础关系模型，本文采用式(1)作为基本回归方程。

ln GDPi，t=β0+β1ln li，t+β2(ln li，t)2+εi，t

(1)

式中：l表示夜间灯光均值；i=1，2，3，…，34表示省份；t=1992，1993，…，2013表示年份。采用该模型的原因有三个。第一，借鉴文献[11]的研究，夜间灯光的二次项被纳入解释变量的讨论中。第二，在Li等[28]的研究框架中，把二次项作为解释变量之一。第三，笔者前期拟合结果显示，非线性模型比其他模型能更好地拟合二者的基础关系。

2 研究结果

2.1 全样本视角

图2展示了全样本夜间灯光数据和GDP的统计值的拟合曲线，在样本取值范围内，拟合GDP随灯光均值递增，且呈现边际效应递减规律。但由于拟合优度仅为41.5%，说明从全样本的角度，仅用灯光数据替代GDP的效率相当有限。

2.2 地区视角

以省级行政区作为基本单位，将每个地区历年的夜间灯光数据与GDP做回归，结果见表2。除香港、澳门、台湾以外，其他地区拟合优度达95%以上，回归方程在1%水平上显著，说明各个地区的拟合结果可靠。此外，除澳门、台湾的常数项、二次项在5%水平上不显著外，其他地区各项回归系数均显著。由于港、澳、台地区的拟合优度及系数的显著性与其他31个省级行政区差异较大，故本节将港澳台地区和其他31个省级行政区分开讨论。

由回归系数β2知，其他31个省级行政区的回归曲线呈U型，其中有16个地区的一次项系数β1小于0，即这些地区拟合曲线最低点对应的ln l大于零。这部分区域包含10个东部地区(北京市、天津市、河北省、上海市、江苏省、浙江省、福建省、山东省、广东省、海南省)、4个中部地区(山西省、安徽省、河南省、湖北省)、2个东北地区(辽宁省、吉林省)，其中大部分地区属于中国东部较发达区域。余下的15个地区的一次项系数β1大于0，即拟合曲线最低点对应的ln l小于零。这部分区域包含12个西部地区(内蒙古自治区、广西壮族自治区、重庆市、四川省、贵州省、云南省、西藏自治区、陕西省、甘肃省、青海省、宁夏回族自治区、新疆维吾尔自治区)、2个中部地区(江西省、湖南省)、1个东北地区(黑龙江省)，其中大部分地区属于中国西部较不发达区域。对比发现，31个省级行政区的GDP均随灯光数据递增，且呈现边际效应递增规律，各地区拟合曲线与统计值的分布相当吻合，统计值紧密地分布在拟合曲线附近，拟合结果对数据的实际规律有较好的反映。不同的是，较发达地区的l取值范围相对较大，较不发达地区的l取值范围相对较小，即中国“发达地区”的灯光均值比“不发达地区”要高，灯光更亮，这与中国地区经济发展水平的特征相符。

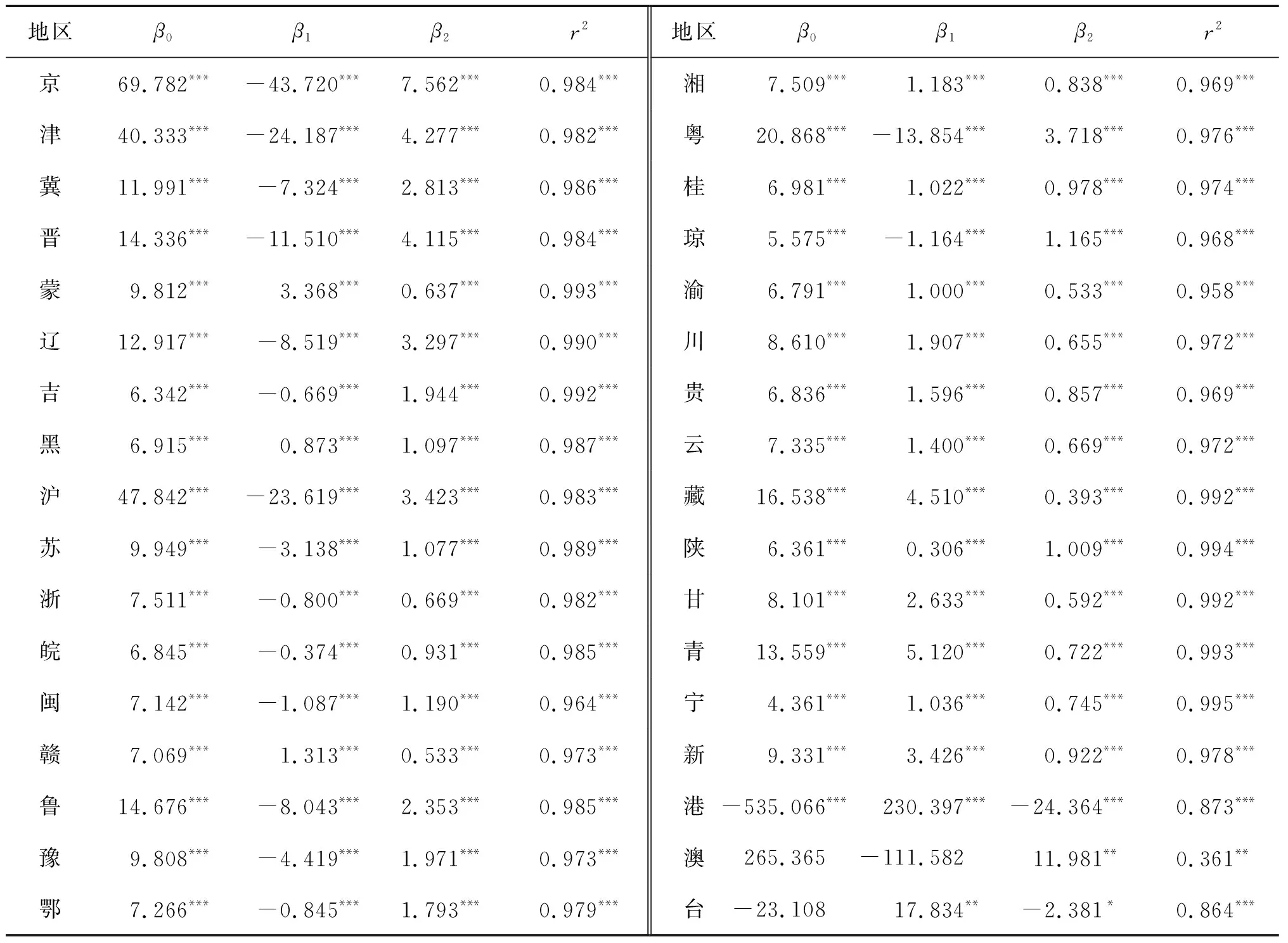
表2 省级地区夜间灯光与GDP回归结果

各地区的拟合图见图3。结合相关数据发现，除了西藏、贵州、重庆、湖南、湖北5个地区外，其他地区灯光均值从1992—1993年提升的绝对值较高，尤其是北京、天津、河北、山西、内蒙古、辽宁、吉林、黑龙江、上海、山东、海南、澳门12个地区，1992—1993年灯光均值的上升幅度非常大。结合相应年份的经济活动发现，1992年邓小平南方谈话开启了中国新一轮的改革开放，极大刺激了中国的经济社会发展；香港地区在1997年灯光均值较上一年有一个大幅的提升，而1997年香港回归中国，与内地的经贸合作显著增多，极大推动了香港经济的发展，这些结果说明夜间灯光能反映全国层面或者地区层面的经济变动。

对于拟合优度较低，且首次拟合各项系数均不显著的澳门地区，以5%为显著性水平进行循环检验，发现该地区回归系数β2不显著，剔除二次项，进行第二次回归得β0=-19.293，β1=5.248，且此时β0、β1均显著，拟合优度为34.42%，仍然较低。结合线性回归拟合图3(a)、图3(f)和统计数据发现，自1997年起澳门的灯光均值几乎保持不变，体现在图中为1997年及以后的统计值对应点几乎没有横向差异，但有纵向差异，即GDP在不断上升，拟合直线不能较好地反映统计值的分布。

同理，对首次拟合二次项、常数项不显著的台湾进行循环检验和再回归，得β0=4.338，β1=1.646，均显著，拟合优度为83.64%，拟合图见图3(a)、图3(g)。结合统计数据知，灯光均值在1997年前上升幅度较大，1997年后上升幅度有限，表现为图中1997年之后的统计值对应点横向差距小，期间台湾地区的GDP自1993到1994年有一个大幅提升之后，上升的幅度也逐渐缩小，且出现了三次回落，拟合效果较差。

香港的拟合优度为87.3%，首次拟合各项系数均显著，结合图3(a)、图3(h)和香港的相关数据发现，其灯光均值从1996年的102.351升至1997年111.552，是一个大幅的提升，上升绝对值达9.201，随后从1999到2013年，灯光均值上升非常缓慢，15年仅上升了0.132，图中表现为右上方统计值几乎没有横向差距，而这期间香港的GDP上升趋势较显著，拟合效果较差。

究其原因，本文认为可能由于地理因素、制度因素使得香港、澳门、台湾地区夜间灯光与GDP的关系和其他31个省级行政区有差异。澳门区域面积仅32.8 km2，1992年起大部分区域已为有灯光区域，即使在1992—2013年间有新增的灯光区域，但因为面积有限，新增的灯光也难以反映，同时中心城区灯光亮度早已达到饱和值，即使中心城区的经济持续增长，灯光数据也无法提升。自1999年起，澳门的灯光均值便保持在148.4，因而不能准确地反映经济发展变化，拟合优度也相对较低。香港地区与澳门类似，区域面积较小，几乎均为灯光点亮的城市地区，故灯光面积上升空间小，难以准确反映经济发展趋势。台湾地区从1995年开始经济发展放缓，经济发展受阻至今还受到制约，因此在1992—2013年期间台湾经济的不正常发展可能是其夜间灯光难以较好反映经济特征的原因。特别地，香港、台湾、澳门地区的灯光增长率和GDP增长率为34个省级行政区最低，还可能和这三个地区特殊的社会制度有关，不同的社会制度产生了不同的生活方式、生产方式、产业结构、风俗文化等，这些经济社会因素导致经济繁荣程度和夜间灯光亮度之间的关系不同于其他31个省级行政区，因此在灯光均值与GDP关系的度量上，会呈现不一样的规律。

从统计数据中还发现，初始灯光均值较低的地区较初始灯光均值较高的地区，在1992—2013年间灯光均值呈现出更快的增长速率，如1992年灯光均值最低的5个地区(西藏自治区、青海省、新疆维吾尔自治区、内蒙古自治区、甘肃省)，在1992至2013年间灯光均值的年增长率分别为12.7%、9.0%、10.0%、8.9%、8.0%，而灯光均值最高的5个地区(天津市、台湾地区、上海市、香港特别行政区、澳门特别行政区)，在这期间的年增长率为4.5%、2.3%、4.1%、1.0%、1.5%。但是GDP增速却未在地区之间呈现类似的规律。一个明显的事实是，初始灯光均值较低的地区均为中国区域面积较广的地区，这些地区大部分为无灯光或低灯光亮度区域，能给予夜间灯光足够的上升空间；而初始灯光较高的地区面积普遍较小，尤其是上海市、天津市、北京市、香港特别行政区、澳门特别行政区，区域内大部分面积为灯光点亮的城市地区，剩下的无灯光或低灯光亮度区域非常有限，给予夜间灯光增加的空间也非常有限，说明地区面积可能是影响夜间灯光与GDP关系的一个外在因素。

考虑到夜间灯光与GDP的相互关系可能受到不同区域尺度的影响，本文在市级层面也进行了夜间灯光与GDP相关性的验证。鉴于数据的可得性，采用27个省会城市的GDP总量和夜间灯光均值数据，仍然用式(1)进行回归。其中，拉萨市GDP缺失了5个年度的数据，西宁市GDP缺失了1个年度的数据，本文用线性插值法进行补齐。回归结果显示，所有城市的回归方程均显著，且拟合优度达到0.943以上，因此对于市级层面的地区，夜间灯光仍然和GDP存在很强的相关性。

2.3 年度视角

以年度为基本分析单位，对历年各地区的夜间灯光和GDP做回归，发现各地区回归系数的符号均一致，回归曲线呈倒U型，二次项系数的绝对值、一次项系数、常数项均随年度递增，表示回归曲线有随年度向坐标轴右上方移动的规律，即随着年度递增，各地区的夜间灯光和GDP也递增。此外，历年的回归方程在1%的水平上显著，各年度的拟合优度介于47%和49.7%之间，代表了年度视角下夜间灯光对GDP的解释程度。进一步对各个年度的回归系数做显著性检验发现，1992和1994年的二次项系数β2在5%的水平上不显著，其他年份的所有回归系数均在5%的水平上显著，特别地，2007至2013年7个年度的各项回归系数的显著性水平达1%。经循环检验，剔除1992年的二次项再回归，得β0=6.372，β1=0.347，此时显著，回归结果为直线；剔除1994年的二次项再进行回归，得β0=6.745，β1=0.384，在1%水平上显著，回归结果为直线。

由于从地区的视角回归时，澳门、香港、台湾的拟合优度相对较低，且在拟合历年夜间灯光和GDP的图形过程中发现，这3个地区离拟合曲线(直线)的距离均比较远，尤其在初始年份，这种现象更明显，但即使只考虑其他31个省级行政区，发现从年度的视角来看，地区之间的横向比较并未呈现出GDP随灯光数据严格递增的规律，即灯光均值越大的地区不一定GDP越高。比如北京市、台湾地区、天津市、上海市、香港特别行政区，这几个地区属于灯光均值最高地区，而其GDP总量并非最高。这几个地区的共同特点是区域面积较小，人均GDP较高，此结果也说明区域面积可能是影响GDP与夜间灯光关系的外在因素。

2.4 整体估计

本节从控制个体效应和时间效应的角度，对整体样本进行估计，以ln l和(ln l)2为自变量，lnGDP为因变量的估计结果见表3。作为参照，首先进行混合回归，采用聚类稳健标准误，由第2行所示，自变量ln l和(ln l)2的系数β1、β2分别为0.248和0.056，在1%水平上通过显著性检验，但是拟合优度仅为0.444。考虑使用固定效应模型，同样采用稳健标准误，估计结果见第3行，β1和β2上升至1.378和0.091，组内r2=0.873。为了确定在固定效应和混合回归中的选择，采用LSDV法进行了F检验，结果见第4行，系数较固定效应估计不变，但r2提升至0.887。输出结果中，所有的个体虚拟变量均显著，认为存在个体效应，不应使用混合回归。随后，在固定效应模型中考虑时间效应，使用双向固定效应模型回归结果见第5行，一次项和二次项系数均不显著。第6行是随机效应估计结果，β1和β2分别为0.950和0.071，组内r2=0.872，对随机效应模型进一步进行MLE估计，LM检验和MLE估计结果均认为随机效应优于混合估计，同时用Hausman检验结果显示应使用固定效应模型，而非随机效应模型。上述过程确定了固定效应模型的适用性，但由于时间效应的加入，使得显著性降低，且估计结果有较大波动，故为了控制宏观环境的变化，以2008年金融危机为分界点设置时间虚拟变量，使用固定效应模型估计结果见第7行，β1和β2较不加时间虚拟变量(第3行)稍有降低，组内r2提升至0.932。从上述整体估计来看，地区层面的GDP与夜间灯光均值存在显著的对数非线性关系。

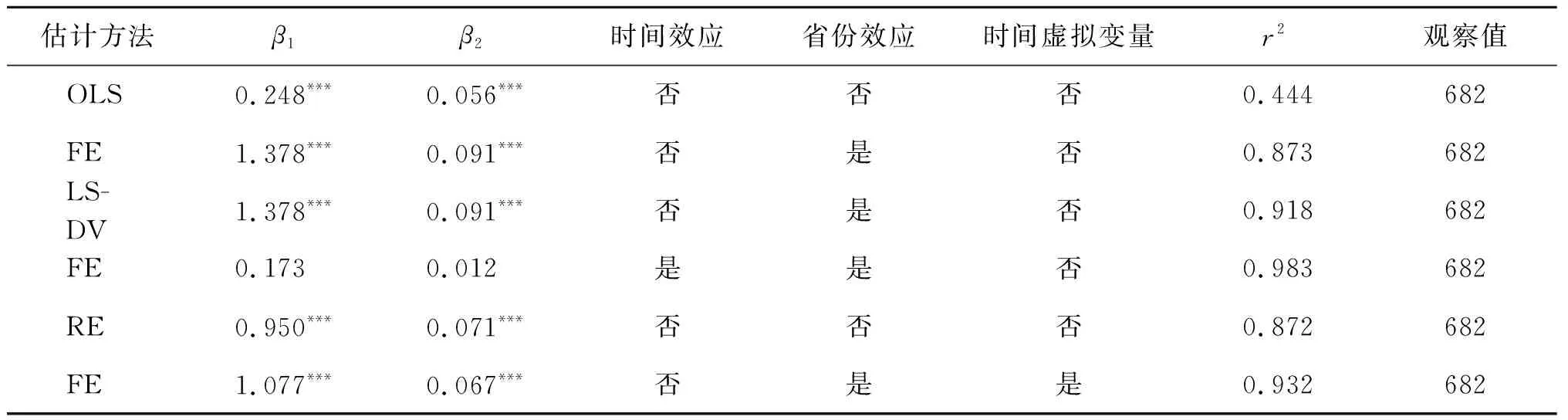
表3 对lnGDP的整体估计结果

2.5 考虑初始条件的方程

本节仍然以地区为分析单位，在借鉴前文分析结果的基础上，从地区视角对夜间灯光与GDP的基本关系进行检验，以发现二者更一般的相关性特征。鉴于港、澳、台地区在上述关系方程中的拟合效果较差，故本节仅对其他31个省级行政区的回归方程进行深入的探索和修正。首先根据拟合曲线的抛物线特征，对回归方程进行配方变形，如式(2)所示。

(2)

式中：β2为原回归方程的二次项系数，表示夜间灯光对GDP影响的速率，即边际递增的速度；-β1/2β2表示回归曲线最低点对应的ln l值。结合拟合曲线与数据比较发现，所有地区曲线最低点对应的ln l非常接近1992年的ln l，因此，本文将各地区1992年的夜间灯光均值对数ln l1992作为自变量，-β1/2β2作为因变量进行回归，发现相关性非常显著，拟合图见图4(a)。

从图4(a)可知，各省该系数与初始ln l1992存在显著正相关，统计值的分布与拟合直线相当吻合，拟合优度达98.1%，拟合直线的斜率为1.069。类似地，β0-β2(β1/2β2)2表示回归曲线最低点对应的ln GDP值，同样，以ln GDP1992作为自变量，β0-β2(β1/2β2)2作为因变量回归，见图4(b)，各地区该系数与ln GDP1992存在显著的正相关，统计值的分布与拟合直线吻合，拟合优度达96.5%，拟合直线的斜率为1.149。

基于上述结果，本文尝试用ln l1992替代-β1/2β2，用ln GDP1992替代β0-β2(β1/2β2)2，再一次将回归方程变形为式(3)。

ln GDPi，t-ln GDPi，0=α1(ln li，t-ln li，0)2+α0

(3)

式中：ln GDPi，0表示各地区1992年的GDP对数；ln li，0表示各地区1992年的夜间灯光均值对数。用式(3)对31个省级行政区进行拟合，结果见表4，所有地区回归方程显著，拟合优度较高，其中天津、河北、山东、河南、广东、海南、新疆的常数项未通过5%水平的显著性检验，其余系数均显著，但其优点是待估参数更少，拟合优度仍然较高。

将式(3)的拟合结果与式(1)的拟合结果对比发现，辽宁、安徽、重庆、四川、贵州、西藏、陕西7个地区使用考虑初始条件的式(3)，更能反映夜间灯光与GDP的相关性；江苏、浙江、广西、青海4个地区的拟合优度在两个方程上无差异；剩下的地区使用式(1)更能反映夜间灯光与GDP的相关性。

表4 式(3)回归结果

3 结束语

本研究揭示了灯光亮度与经济活动的高度相关性，在省级和市级区域层面用易于获取、客观而非人为的夜间灯光均值作为GDP的替代变量具有合理性。原因有二。第一，回归结果显示中国34个省级行政区和27个省会城市夜间灯光与GDP呈现显著的正相关关系，在一元二次对数方程的关系模型中，除港、澳、台以外的31个省级行政区拟合优度较高，GDP随灯光均值递增且边际效应递增，中国发达地区夜间灯光较不发达地区更亮，这些结果说明夜间灯光能反映地区的经济发展水平。第二，结合数据与现实经济发展实际发现，夜间灯光能反映全国层面或者地区层面的经济变动。

夜间灯光与GDP仍然存在一定的差异，在用夜间灯光度量GDP时可以通过加入辅助变量的方式来提升替代的准确度。因为夜间灯光和GDP的线性或非线性相关趋势不存在简单的横向可比性，灯光均值最高的几个小面积地区，其GDP总量并非最高，说明加入辅助变量(如地区面积)会提高夜间灯光作为经济发展替代变量的准确度。同时，制度因素也是在分析不同制度地区时可以考虑的辅助变量，香港、台湾、澳门地区的拟合优度不高，除了可能和区域面积有关之外，也可能由于不同的社会制度导致经济繁荣程度和夜间灯光亮度之间的关系不同于其他31个省级行政区，因此在灯光均值与GDP关系的度量上，会呈现不一样的规律。

本研究从回归分析结果中发现了夜间灯光与GDP的相关性可能受初始条件影响的特点，并基于该发现对二者的关系方程做出了调整，调整后的方程对辽宁、安徽、重庆、四川、贵州、西藏、陕西7个地区的拟合优度更高。该方程能以更少的待估参数来反映夜间灯光与GDP的相互关系，并突出了初始条件的重要性，为相关地区的研究提供了可借鉴的分析框架。