基于Chen NDVI模型的NDVI尺度转换分形特性分析

栾海军，邢宸硕，张荣凯，何原荣，贺秋华

(1.厦门理工学院 计算机与信息工程学院，厦门 361024；2.厦门理工学院 数字福建自然灾害监测大数据研究所，厦门 361024；3.洞庭湖区生态环境遥感监测湖南省重点实验室，长沙 410008)

0 引言

遥感地表参数的尺度转换问题是定量遥感研究中一个基础且重要的问题，许多学者对包含NDVI在内的多种地表参数进行研究并获得多种转换方法，通常包括统计学、物理模型及数学解析等几类方法，上述方法各有优劣、不一而足[1]。除上述方法外，亦有学者尝试基于分形理论进行遥感地表参数空间尺度转换研究。

在定量遥感研究中，分形方法不仅较多地应用于遥感影像地表形态(空间结构)的刻画[2]，其在尺度转换研究中亦有更多的应用。一方面，Zhang等[3-4]、栾海军等[5-6]、Wu等[7]利用信息维、相似维方法对LAI、NDVI升尺度转换特性进行一系列的研究；另一方面，Kim等[8]基于分形理论建立遥感土壤含水量的空间降尺度转换关系，而Zhang等[9]将分形方法应用于遥感土地利用覆盖/覆被的降尺度转换研究中。学者们不仅关注“空间尺度”，基于多重分形理论的遥感地表参数时空尺度转换耦合模型的构建与应用亦处于发展之势[10]。

建立遥感地表参数的分形尺度转换模型，估算不同时空尺度上的遥感地表参数“理论值”，可用于遥感卫星发射前的应用效能评估与论证、发射后的产品“真实性检验”，并为破解遥感卫星空间-时间分辨率的“固有”矛盾提供重要数据支撑，具有重要的理论价值与应用潜力。但是，针对分形方法在定量遥感尺度转换研究中的应用，部分学者认为分形方法适用于长度、面积等地表几何属性的尺度转换，不适于地表物理属性的尺度转换研究[11]。“分形方法是否适用于定量遥感地表参数的尺度转换研究”仍有待进一步探讨论证。文中将进一步进行此论证研究。

1 研究区与研究数据

选取以福建省厦门市为核心区的矩形实验区，矩形区域便于地表参数的尺度转换研究。厦门环境适宜，人们生产活动兴盛，地物类别丰富。因此，研究区下垫面呈现较显著的空间异质性，将引起遥感地表参数(如NDVI)的显著尺度效应，进而为本次研究提供了重要基础条件。

实验影像为研究区2017年1月3日的Landsat 8 OLI影像。OLI影像进行大气校正时需要用到的研究区高程、气象参数等基本参数，可由厦门市官方网站(http：//www.xm.gov.cn)等网站获取。此外，在研究区内进行野外采样，按几何校正、分类结果验证两种用途共采集地面控制点85个、地物分类结果验证样点615个。接下来，进行实验数据预处理。

对OLI影像进行大气校正、几何精校正，所得影像如图1所示。

参考研究区的地物状况，并综合考虑影像识别能力、尺度转换研究需要，本次实验确定的分类体系包含：林地、建设用地、水体、农田、裸地、滩涂和沙地7种地类。若将影像分为两类，则上述7类中保留水体，其他地类统一划分为陆地。基于eCognition软件对研究区OLI影像进行面向对象分类，获得2类、7类共两种分类结果，如图2所示。利用野外实测样点进行7类分类结果验证，由混淆矩阵计算得出：总体分类精度为79.5%，Kappa系数为0.750 8，表明分类结果精度较高，可满足进一步的研究需要。

由于尺度效应与下垫面空间异质性关系密切，不同的地物类别及组合对NDVI尺度转换特性影响重大，故将选择包含不同地物类别的多个典型样区(表1)进行研究。

表1 OLI影像上所选取样区

2 研究方法

栾海军等[12]研究表明：融入精细地类信息的改进后Chen NDVI模型在精细、定量刻画不同地类对NDVI尺度效应显著性影响方面更有效，是一种有效的升尺度转换模型。本次研究的总体技术流程是：利用厦门研究区OLI影像分类结果(尤其是较精细分类结果)，融入传统及改进的两类Chen NDVI尺度转换模型，实现30 m OLI NDVI影像升尺度转换，获得不同升尺度影像；结合NDVI分形尺度转换构建模型，为不同样区构建模型，对结果进行分析、获取评估结论。各模型的构建方法依次描述如下。

构建传统及改进的Chen NDVI尺度转换模型如式(1)至式(3)所示。

(1)

(2)

(3)

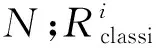
构建NDVI分形尺度转换特性分析模型。在双对数直角坐标系下，NDVI升尺度影像与空间尺度参数的关系模型如式(4)所示。

(4)

式中：NDVI为基础中高空间分辨率影像尺度(如OLI影像30 m)及其升尺度影像的NDVI数值；scale定义为分形计算所需的尺度因子，即尺度比值“上推尺度/基础中高空间分辨率影像尺度(如OLI影像30 m)”；对尺度因子的倒数(1/scale)与NDVI数组分别取以2为底的对数，并对两数组进行直线拟合，此过程即为分形计算，式中d即是拟合直线的斜率，b为拟合直线的截距，b是常量。与之前研究不同的是，本研究中不同尺度上NDVI数值取各尺度上整幅影像的均值、方差、方差除以均值共3种统计量逐一进行实验，以获取更为全面的实验结果。

进一步，一组统计学评价指标(r、p、rlo、rup)被选取用于式(4)的评价模型。其中，r表示拟合直线与真实曲线的相关系数(r越大表明线性拟合程度越好)，当p较小(小于0.05)时说明计算的r值是有意义的，rlo、rup为相关系数r的95%置信区间下界与上界值，表明r的真实值不足rlo的概率小于5%。

为增进对比，在直角坐标系下构建NDVI升尺度影像与空间尺度参数的关系方程，如式(5)所示。

NDVI=dlog2scale+b

(5)

式中各参数含义与式(4)相同。该模型的统计学评价指标同式(4)表述的模型。

3 研究结果与分析

3.1 研究结果

1)基于传统Chen NDVI模型。基于OLI影像，利用传统Chen NDVI模型(式(1)至式(3)，地物类别为两类情况)可得不同空间升尺度NDVI影像。对表1中所选的5个样区，利用式(4)、式(5)依次建立其NDVI升尺度影像与空间尺度参数的关系模型，如表2、表4所示，各拟合模型的评价参数如表3、表5所示。表2、表4中子图的横坐标scale代表不同的上推尺度与基础影像尺度(这里是30 m)的比值，纵坐标代表各上推尺度下的NDVI影像输入类型(均值mean、方差variance或者方差/均值variance/mean中的一种)或者其对数值；original data(蓝色方形点)代表基于实际影像(这里为OLI影像)不同上推尺度的统计数据所绘的图形，fitting data(红色菱形点)代表基于实际统计数据所得拟合直线(即式(4)、式(5)所示)上各尺度计算数据所绘的图形。表3中，“-”表明无法获得拟合模型或者所得拟合模型统计学评价指标(r、p、rlo、rup)不符合要求、模型无效。

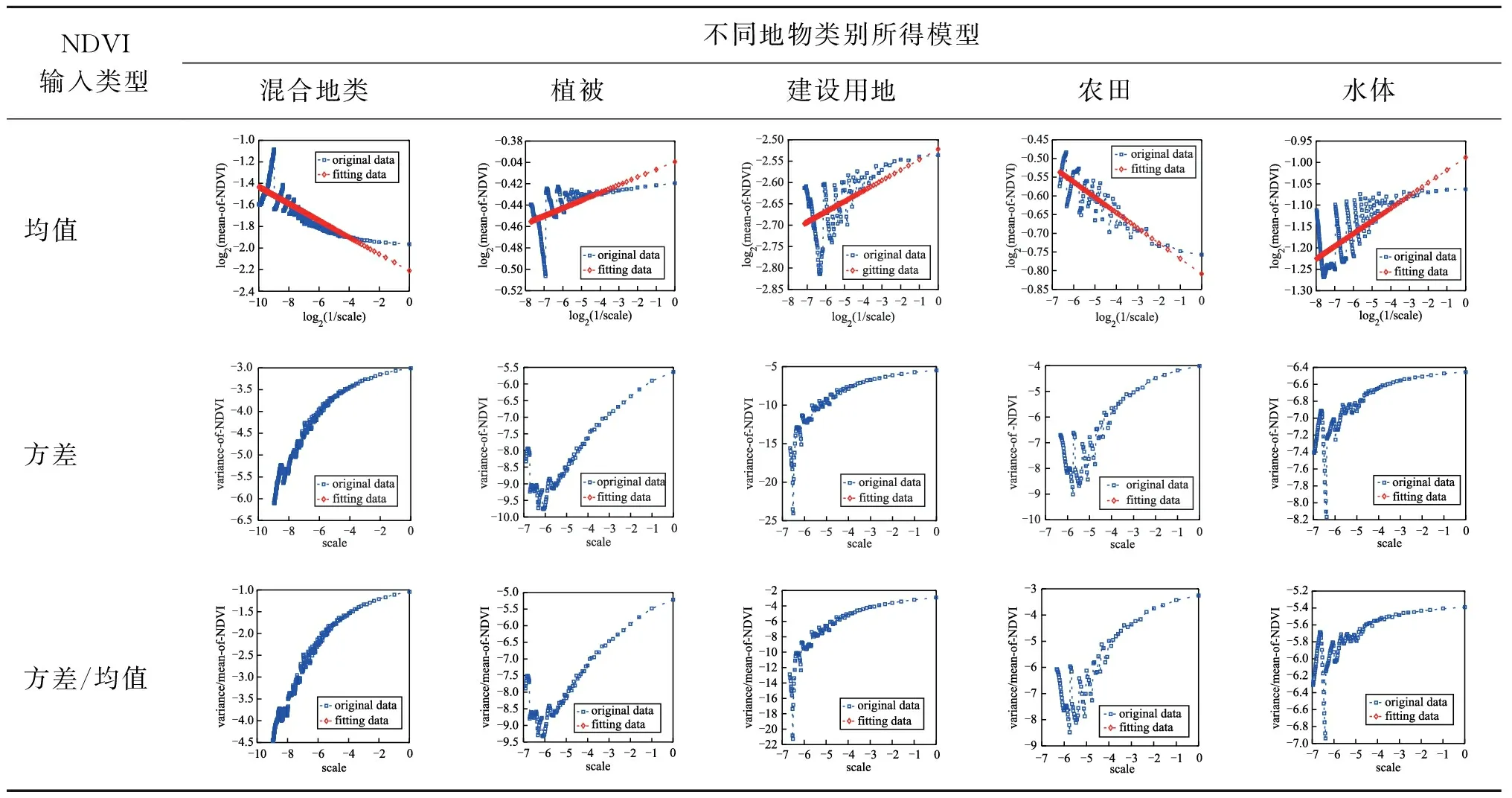
表2 双对数直角坐标系下所得模型结果(基于传统Chen NDVI模型)

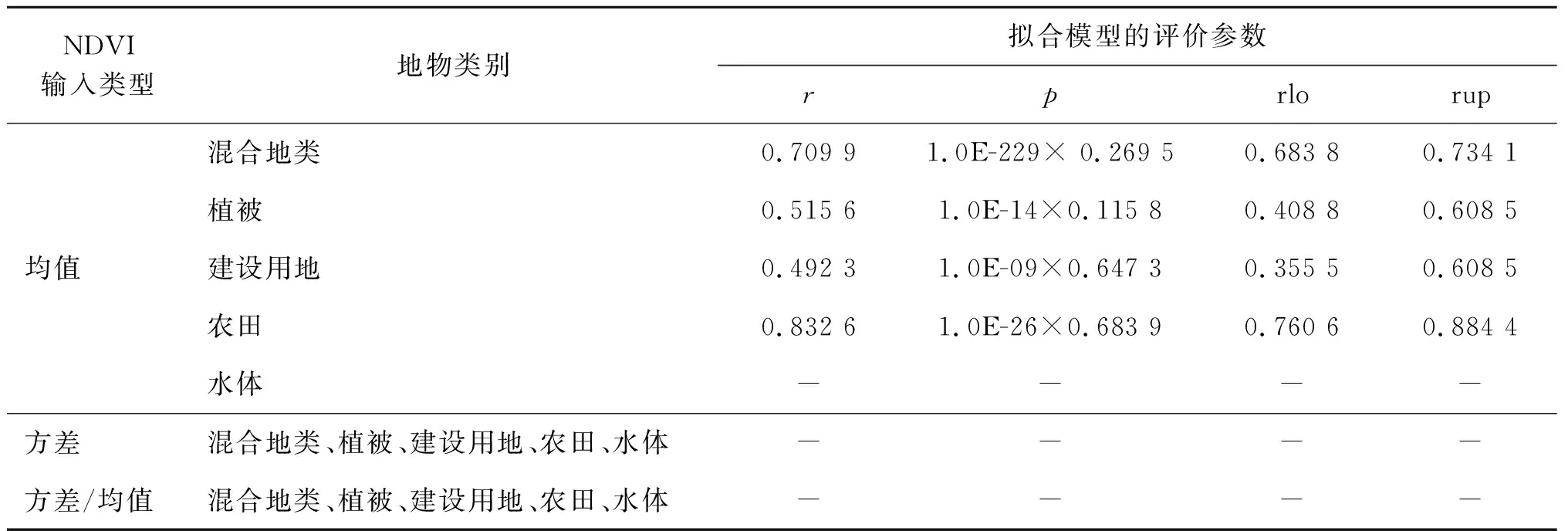
表3 双对数直角坐标系下(基于传统Chen NDVI模型)所得结果评价

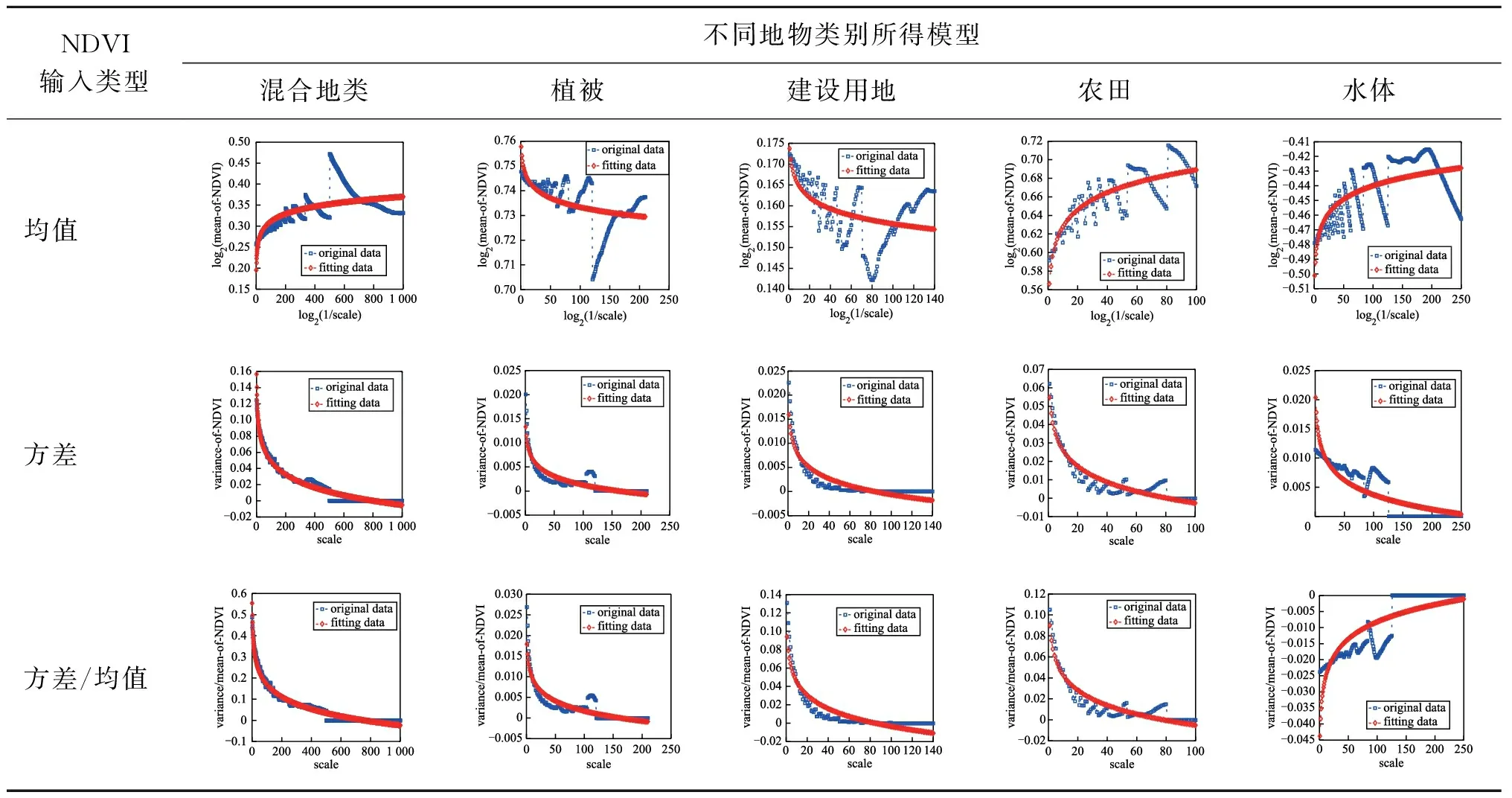
表4 直角坐标系下所得模型结果(基于传统Chen NDVI模型)

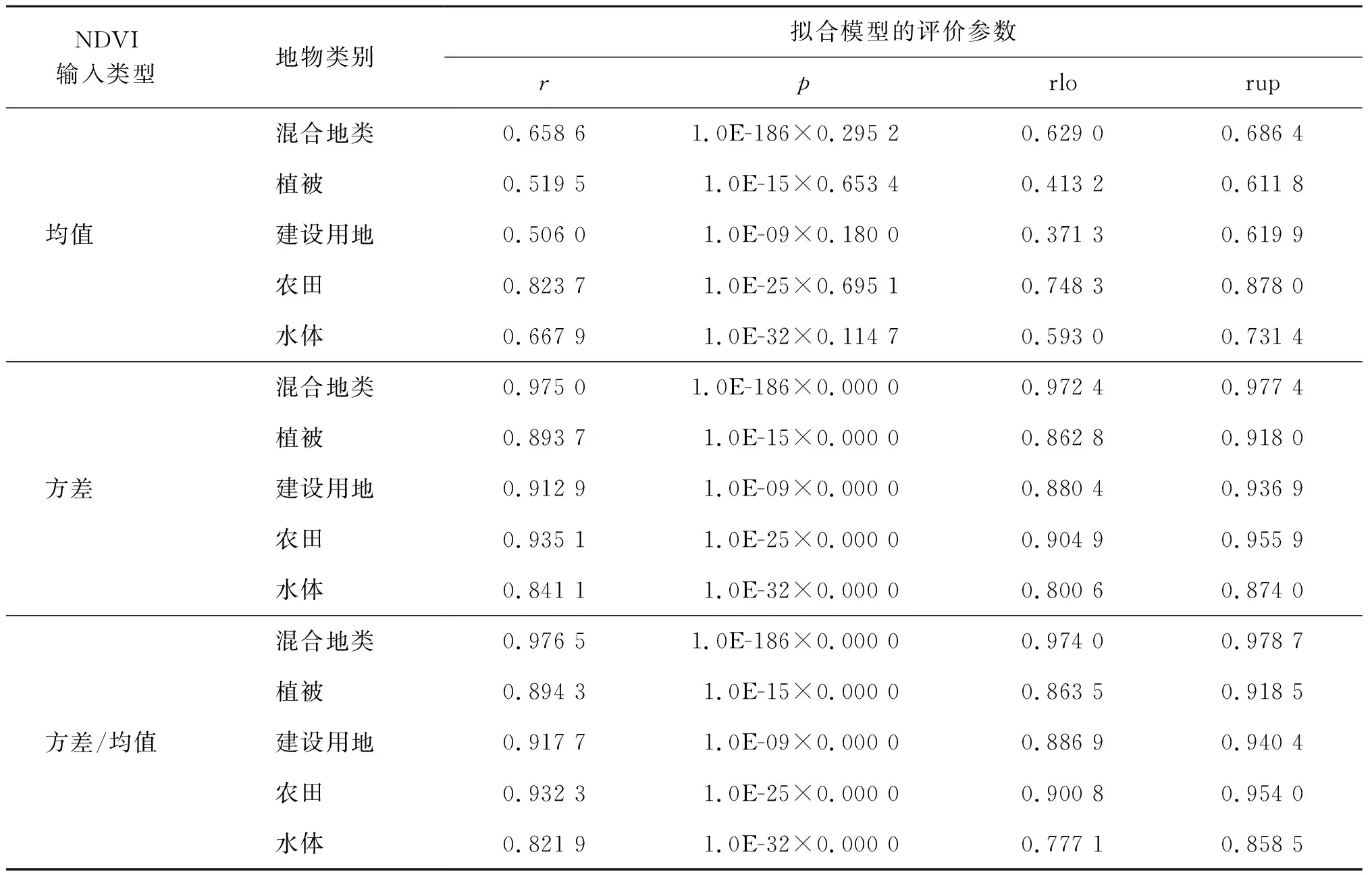
表5 直角坐标系下(基于传统Chen NDVI模型)所得结果评价

2)基于改进的Chen NDVI模型。基于OLI影像，利用改进的Chen NDVI模型(式(1)至式(3)，地物类别为7类情况)可得不同空间升尺度NDVI影像。对表1中所选的5个样区，利用式(4)、式(5)依次建立其NDVI升尺度影像与空间尺度参数的关系模型如表6、表8所示，各拟合模型的评价参数如表7、表9所示。表6、表8中各参数的含义与表2、表4中相同。表7中，“-”表明无法获得拟合模型或者所得拟合模型统计学评价指标(r、p、rlo、rup)不符合要求、模型无效。

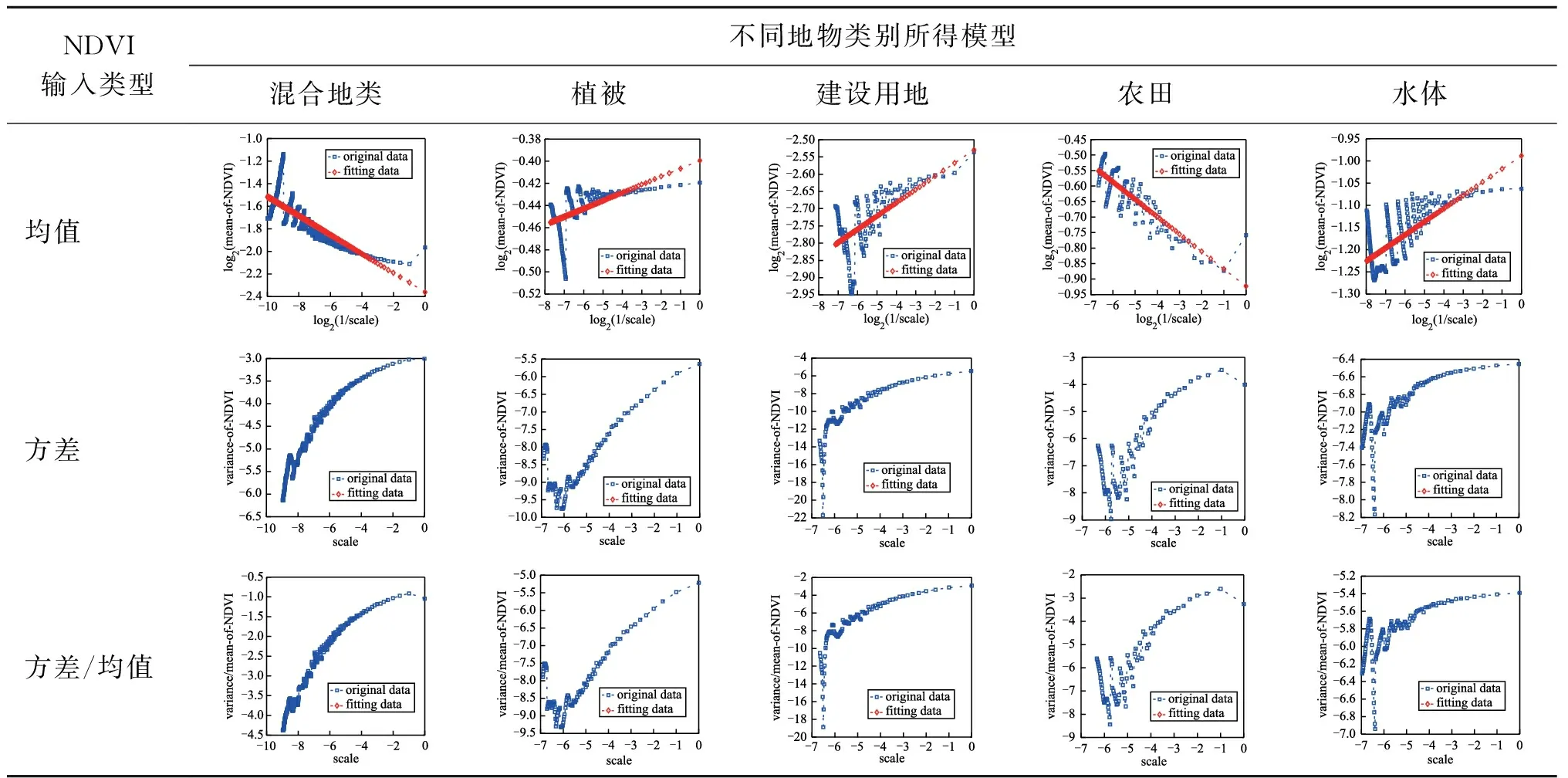
表6 双对数直角坐标系下所得模型结果(基于改进的Chen NDVI模型)

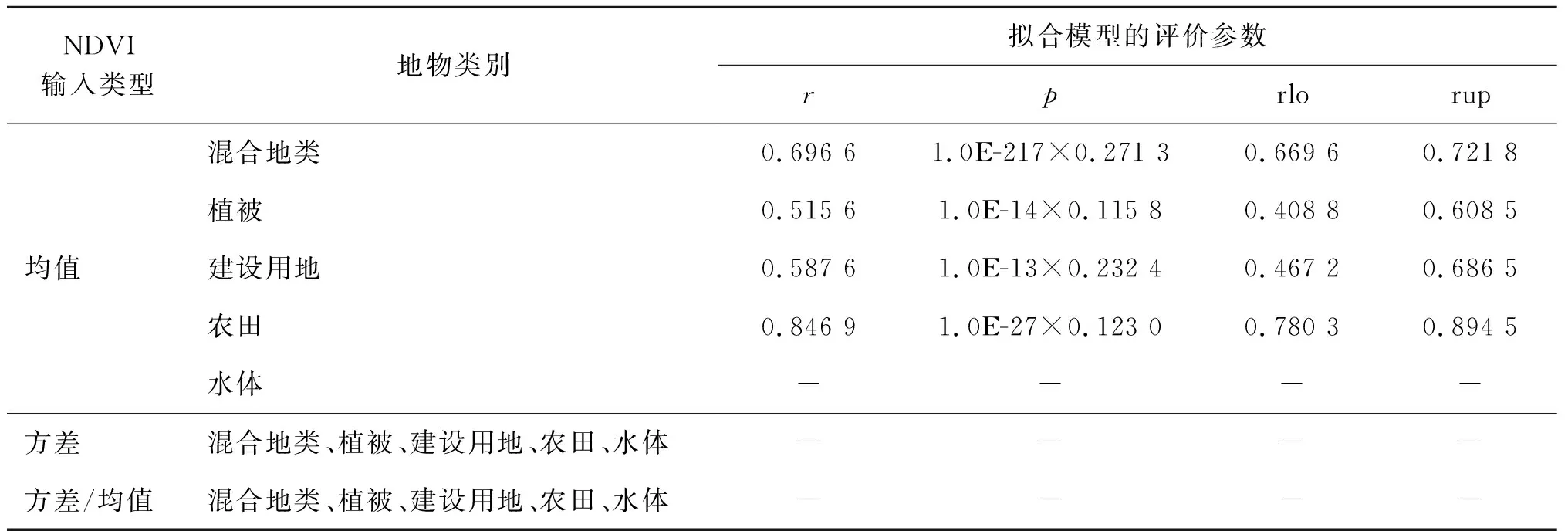
表7 双对数直角坐标系下(基于改进的Chen NDVI模型)所得结果评价

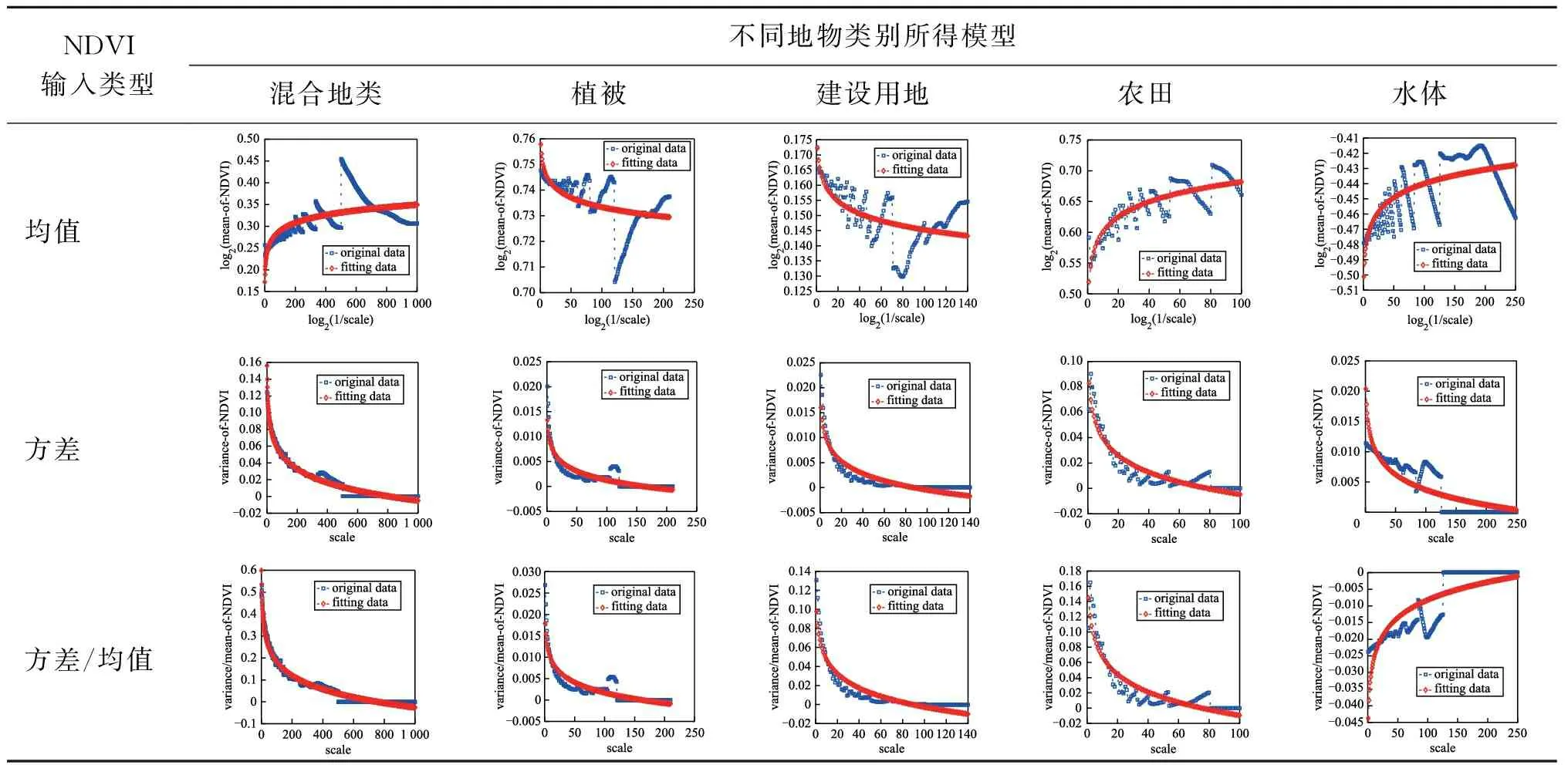
表8 直角坐标系下所得模型结果(基于改进的Chen NDVI模型)

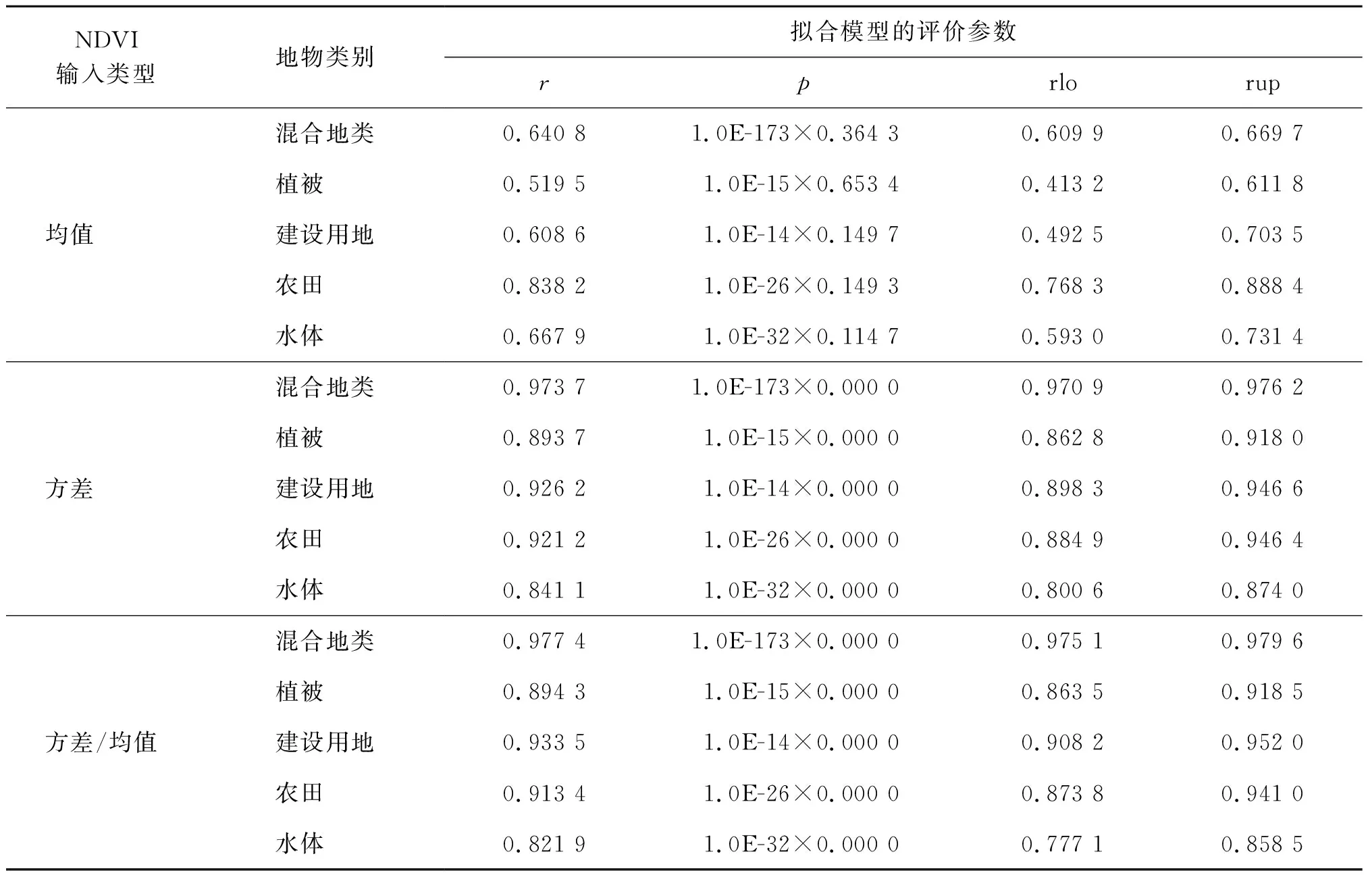
表9 直角坐标系下(基于改进的Chen NDVI模型)所得结果评价

3.2 结果分析

对表2至表9结果进行分析，可得以下结论。

1)若NDVI输入类型为均值，NDVI尺度转换特性更符合双对数直角坐标系下的线性函数关系，即分形特性；若NDVI输入类型为方差、方差/均值，NDVI尺度转换特性更符合直角坐标系下的对数函数关系。

2)不同地物类别的NDVI尺度转换特性不同，相比较其他地物类别，农田在两种Chen NDVI模型及两种空间直角坐标系下所得拟合模型皆表现出显著的线性规律，尤其是其NDVI尺度转换分形特性表现显著。

3)综合而言，从不同地类实验结果来看，可以认为NDVI尺度转换结果具有分形特性(水体作为相对均一的地类，其NDVI尺度效应不显著是合理的)，但NDVI尺度转换具有更为显著的直角坐标系下对数函数关系特性。

3.3 讨论

1)NDVI尺度效应产生原因分析。NDVI的空间不均一性是造成NDVI尺度效应的根源。为定量描述实验区NDVI空间异质性的存在，可采用影像平均空间异质性指数(spatial heterogeneity index，SHI)[14]评价影像的空间异质性。

对于各地类，利用融合精细地类信息的Chen NDVI模型估算各升尺度NDVI影像，进而可计算得到不同上推尺度影像的SHI，对尺度-SHI数组绘图，可得图3。图3中，横坐标中scale代表各上推尺度，其含义与式(4)中的相同；纵坐标mean SHI即在对应的各上推尺度下影像的平均空间异质性指数。

若各地类NDVI空间分布均一，不存在异质性，则各上推尺度影像SHI相同。分析图3可知，不同上推尺度影像间SHI变化显著，这说明各地类NDVI存在较为显著的空间异质性，且异质性程度大体上按如下顺序增强：水体→植被→建设用地→农田、混合地类。据作者此前的研究[15]可知：影像平均异质性指数与地类复杂性及地类的破碎程度密切相关。当地类简单、分布集中时，由于地类分布空间相关性的存在，影像尺度较小时，相邻像元性质相近，像元SHI较小，影像的平均SHI较小；影像尺度上推时，相邻、性质相近的像元聚合，上推影像像元间差异增大，像元SHI增大，影像的平均SHI增大。当地类复杂、分布破碎，影像尺度较小时，相邻像元性质差异表现显著，像元SHI较大，影像的平均SHI较大；影像尺度上推时，相邻、性质相异的像元聚合，上推影像像元间差异弱化，像元SHI减小，影像的平均SHI减小。图3揭示了NDVI存在尺度效应的根本原因，同时为进行NDVI尺度转换研究的必要性提供了支撑。

2)“类NDVI”地表参数通用尺度转换模型建立。文中以改进的Chen NDVI模型为基础获取不同尺度NDVI影像，进而基于分形方法研究其尺度转换特性。进一步分析，改进的Chen NDVI模型可看作一种扩展的、近似的几何光学模型(geometrical optical model，GO model)。一方面，在中等空间分辨率影像上(如OLI),该模型不考虑阴影效应；另一方面，它将地类从2类扩展到7类。除NDVI外，对于诸多仅以不同波段地表反射率为反演函数独立参数的“类NDVI”地表参数，其融入精细地类信息的尺度转换模型与改进的Chen NDVI模型类似，其通用模型可参见文献[16]。

上述“类NDVI”地表参数通用尺度转换模型可以在不同地类对地表参数尺度效应精细化、定量化影响研究中发挥重要作用。以此模型为基础，同时结合文中的分形研究方法，可以对其他“类NDVI”地表参数尺度转换分形特性进行分析研究。

本研究的不足与改进方向有以下几点。

1)Luan等[17]研究表明，在某些区域当尺度转换倍率较大时(如从30 m OLI NDVI影像转换至240 m NDVI影像，倍率为8)，Chen NDVI尺度转换模型存在一定程度误差，即该模型的鲁棒性仍有待提高。故后续可选取精度更高的NDVI尺度转换模型获取空间升尺度影像进行文中的研究，如引入基于泰勒级数展开方法的NDVI尺度转换模型。

2)构建像素级别的NDVI尺度转换特性刻画模型。作为影像最基本的统计量，均值、方差可以表征影像“整体”特点，但是距离影像特性的“像素级别”刻画仍存在差距，建议对研究中所列方程进行组合、联立、约简，利用方程组联合表达地表参数尺度转换特性，更为科学。

3)宫鹏[18]认为，国外遥感研究定位于满足实际应用，多以遥感为技术方法，而国内多侧重于方法的修改完整，对遥感的根本目标有所忽略。基于该思想，认为：遥感地表参数的尺度效应问题不是孤立存在的，不同尺度下遥感地表参数估算是否准确不是绝对的，应该在具体的应用场景中加以看待，利用更多环境参数与变量、甚至所在圈层系统的运行状况作为共生伴随条件以及约束，通过检验它们之间的协调度、平衡性综合评估不同尺度地表参数的准确性。

4 结束语

本文以厦门为研究区，基于传统及改进的Chen NDVI尺度转换模型，实现30 m OLI NDVI影像升尺度转换，获得不同升尺度影像，进而结合NDVI分形尺度转换模型分析NDVI尺度转换特性。综合而言，认为：NDVI尺度转换结果具有分形特性，但NDVI尺度转换具有更为显著的直角坐标系下对数函数关系特性。基于此结论，后续可尝试基于分形理论构建NDVI尺度转换模型，并用于低空间分辨率NDVI产品(如MOD13 Q1)的真实性检验。本文的研究仍存在部分问题，有待后续着力解决。而文中所提出的融入精细地类信息的“类NDVI”地表参数通用尺度转换模型及尺度转换分形特性研究方法具有一定的代表性，值得参考。