结合并行CNN与极限学习机的高光谱图像分类

任彦，高晓文，杨静，叶玉伟，王佳鑫

(内蒙古科技大学 信息工程学院，内蒙古 包头 014010)

0 引言

高光谱三维图像数据包含了大量空间和光谱信息，能反映出丰富的地物信息，因此被广泛应用于生态环境监测[1]、矿物探测[2]、医学图像[3]、农作物病虫害防治[4]等领域。高光谱图像数据结构复杂，尤其是在样本数少、样本类间信息相关性强的情况下实现精确分类十分困难，并且随着光谱波段数量的增加，会出现分类精度下降的休斯现象[5]。

近年来，支持向量机[6]、随机森林(random forest，RF)[7]、马尔可夫条件随机场(markov random field，MRF)[8]等方法被应用于解决高光谱图像遥感分类技术中的上述难题。Heras等[9]将极限学习机(extreme learning machine，ELM)应用在分类问题中并取得了良好的效果，相比SVM的分类精度和速度有明显改善。Yang 等[10]2020年在树种识别实验中，采用粒子群优化极限学习机方法实现的分类精度优于线性贝叶斯正态分类器和k近邻算法。Gao 等[11]将并行异构极限学习机(parallel extreme learning machine，PELM)应用于锂电池寿命预测中，运行效率远高于ELM。由于ELM的特征提取能力较弱，将其应用于高光谱图像的分类技术中无法取得良好的效果，Cao 等[12]采用CNN提取高光谱图像特征，并利用ELM对其进行特征分类，取得了良好的效果。

高光谱图像存在“同物异谱”和“异物同谱”现象，上述方法只考虑了图像的光谱信息，没有考虑空间的上下文信息，所以分类结果往往伴随有许多噪点，如何充分利用空间信息是近几年研究人员一直关注的热点问题。Fauvel等[13]指出对像素及其邻域进行特征提取时可获得图像的空间信息。Fang等[14]将每个像素定义为一个局部区域，结合局部区域内的训练样本，采用自适应系数策略来表示高光谱图像的空间信息。Chen 等[15]使用线性滤波器提取空间边缘和纹理特征，极大地改善了高光谱图像的分类精度。

传统方式提取空-谱联合特征能力十分有限，考虑到深度学习应用在图像分类的良好效果，Chen 等[16]2014年利用堆栈式自动编码器提取特征，将深度学习的概念引入到高光谱数据的分类中，2015年在充分考虑空间信息的基础上，使用深度置信网络提高了高光谱图像的分类精度[17]。随着深度学习的发展，人们开始将CNN应用于高光谱图像的分类，Hu等[18]采用1D-CNN完成了光谱特征提取，Makantasis等[19]2015年使用2D-CNN提取高光谱图像空间邻域的特征，Chen等[20]提出的3D-CNN网络分类精度优于2D-CNN网络，但计算过程中参数较多。Lee等[21]提出基于上下文信息的深度CNN，利用多尺度滤波器获得空间和光谱联合特征图。Fang等[22]利用2D-CNN提取空间信息，1D-CNN提取光谱信息，相比三维卷积(three-dimensional convolution，3D-CNN)减少了参数量，提升了运算速度。

综上，CNN具有较强的特征提取能力，PELM分类效率较高，本文充分结合二者的优点，提出一种新型的空-谱联合SSCNN-PELM(spatial-spectral convolutional neural network and parallel extreme learning machine)高光谱图像分类模型，该模型采用并行CNN结构实现对高光谱图像空间特征和光谱特征的提取；采用PELM实现高光谱图像的信息融合和高精度分类。

1 理论基础

1.1 PELM

ELM具有输入权重及偏差随机设定、权重一次性求解的特点。输出权重一旦确定，便可确定ELM的唯一模型。然而ELM也存在矩阵运算及逆运算会占据大量运行时间等缺点[23]。

PELM是在ELM的基础上提出来的，该模型把输入层的数据通过不同的非线性激活函数同时映射到并行隐藏层，两个隐藏层同时进行计算求出网络的输出权重，进而求出网络的输出值，实现在减少网络运算时间的同时提高模型的分类精度。

1.2 空-谱联合卷积神经网络

CNN的特征提取能力在图像识别、自然语言处理等领域有广泛的应用。2D-CNN通常应用于提取图像的深层特征；1D-CNN能提取深层语义特征，常应用于自然语言处理、光谱图像分类等领域。

CNN网络一般由卷积层、池化层、全连接层等组成。其中卷积层提取深层特征，池化层降低时间和空间复杂度，全连接层进行特征融合。空-谱联合卷积神经网络(spatial-spectral convolutional neural network，SSCNN)模型由两个并行的CNN模型组成，2D-CNN模型提取全部空间特征和部分光谱特征，1D-CNN提取光谱特征。2D-CNN输入数据经过2D卷积核提取特征，1D-CNN使用1D卷积核代替2D卷积核作用于输入向量。

2 SSCNN-PELM模型设计

高光谱数据类间特征十分接近，使用线性分类器很难达到预期效果，使用传统的特征加权融和方式很难充分结合空间和光谱特征。PELM的特征提取能力不足，但PELM的两个输入层权重和隐藏层的偏差可以随机设定，且设定后不需要再反向调节，减少了网络的运算量；隐藏层和输出层之间的连接权值也不需要再迭代调整，可以通过方程组一次性求解。因此PELM能充分结合光谱和空间信息且分类精度高。

由SSCNN负责提取深层空间特征和光谱特征，PELM实现特征融合与分类，SSCNN使用softmax作为分类器进行训练，得到特征提取器后使用PELM代替softmax进而得到最终的分类结果，充分发挥了SSCNN特征提取能力强及PELM分类精度高、速度快的优点。SSCNN-PELM模型整体框图如图1所示。

针对2D-CNN中高光谱图像全部波段输入网络中会导致参数量过大、计算时间增加的问题，利用主成分分析法(principal components analysis，PCA)将高光谱数据降维，得到数据的主要特征分量。文献[24]通过实验验证，在降维至10～30个波段范围内时高光谱数据能保留完整的空间信息和大部分光谱信息，同时可以减少参数量，避免因数据维度过多造成的休斯现象。2D-CNN模型由输入层、两个卷积层、两个全连接层构成，将图像分割成m×n×l大小的数据块输入网络，采用线性整流函数(rectified linear unit，ReLU)作为卷积层激活函数，每个卷积层后添加归一化层和随机失活层，优化器选择带牛顿动量自适应学习率的梯度下降法(nesterov accelerated adaptive momentestimation，NADAM)。1D-CNN由输入层、两个卷积层、一个池化层、两个全连接层构成，池化层选择最大池化，为防止过拟合添加随机失活层，优化器选择随机梯度下降法(stochastic gradient descent，SGD)。CNN网络的全连接层输出数据直接输入PELM网络，PELM网络为了增强学习能力选择两个不同的激活函数。

3 实验结果与分析

实验硬件环境为Intel Core i9-9900KF CPU @ 3.60 GHz，NVIDIA RTX2080 GPU，32 GB内存。使用python语言编程，其中SSCNN模型搭建部分使用tensorflow框架。实验中每类样本随机选取10%作为训练样本，90%作为测试样本，使用每类样本分类精度、总体分类精度(overall accuracy，OA)、平均分类精度(average accuracy，AA)、Kappa系数、分类时间来评价实验模型的性能，实验重复10次取平均值。

3.1 数据集

为了体现SSCNN-PELM模型的泛化能力，实验选择Indian pines和Pavia university两个数据集验证。Indian pines图像由AVIRIS传感器采集，光谱范围是400～2 500 nm，数据维度为145×145×200，空间分辨率20 m，共有16类样本，其中标记样本总数10 249。样本类别名称、颜色表示、样本数量见表1，数据集的遥感图像见图2。Pavia university图像由ROSIS传感器采集，光谱范围是430～860 nm，数据维度是610×340×103，空间分辨率1.3 m，共有9类样本，标记样本总数42 776。样本类别名称、颜色表示、样本数量见表2，数据集的遥感图像见图3。

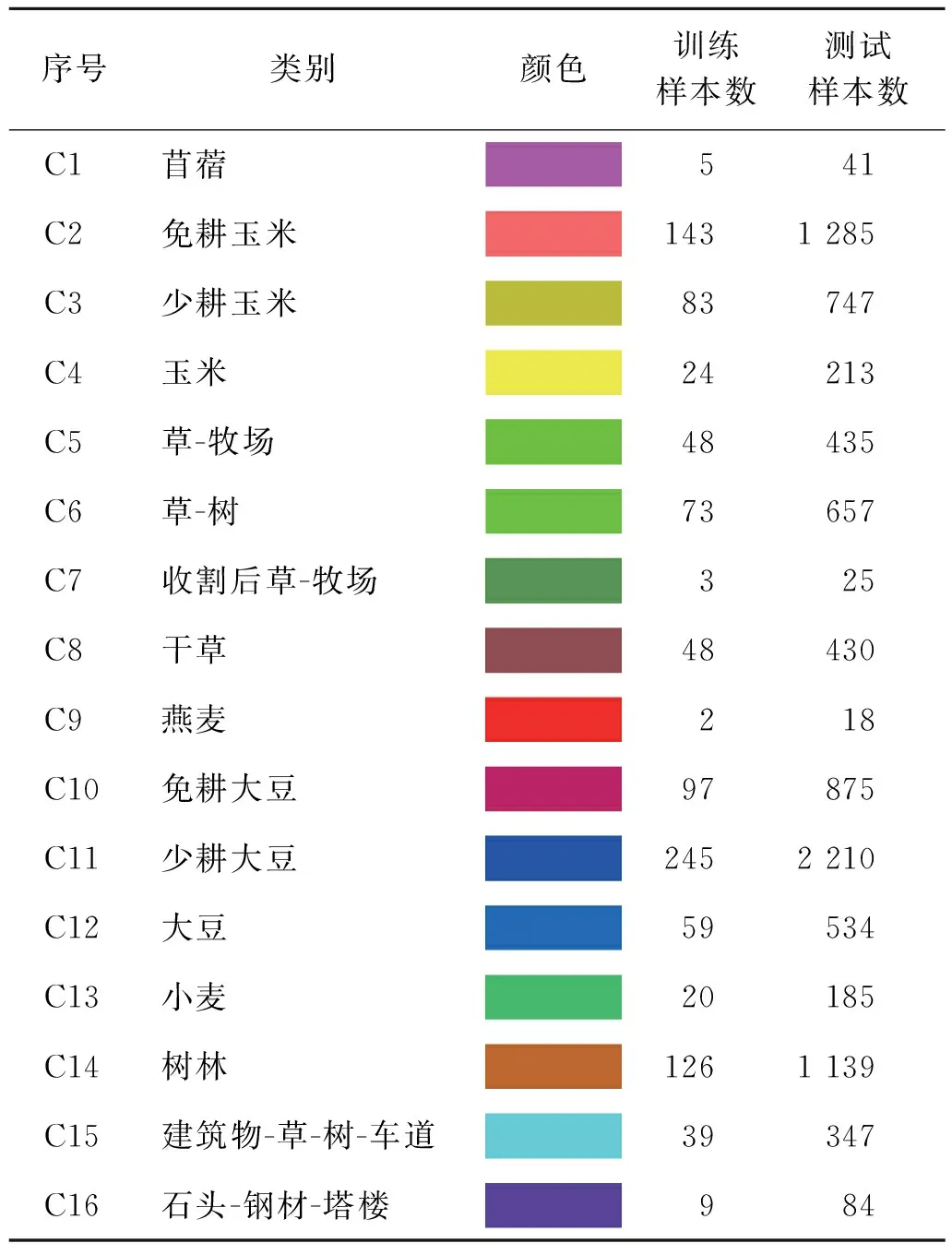
表1 Indian pines数据集

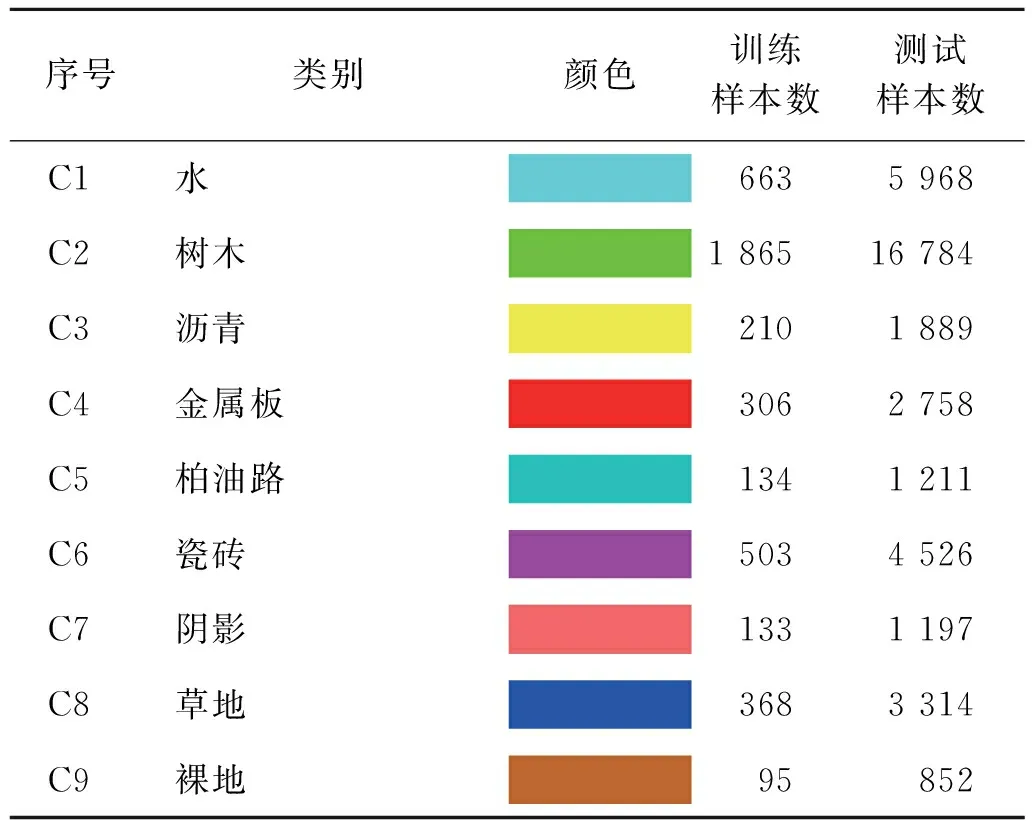
表2 Pavia university 数据集

3.2 实验参数

1)Indian pines数据集。该数据集分类难度较大，表3、表4是各模型的对比实验结果，其中SVM核函数选择linear，ELM隐藏层节点数为500，激活函数为sigmoid；PELM的两个ELM网络结构隐藏层数都设置为1层，节点数为500，激活函数分别选择sigmoid和tanh；2D-CNN邻域大小选择25×25，epoch设为300；3D-CNN像素块大小设置为11×11×30，epoch设为300。

SSFCN-PELM模型在2D-CNN部分输入为45×45×10数据块，使用两个卷积层，卷积核数量分别设为10、30，大小设为3×3，学习率设为0.001，epoch设为50，1D-CNN部分使用两个卷积层，卷积核大小设置为5，数量为64，学习率设为0.001，epoch设为100。图4是模型在两个隐藏层不同节点数影响下的分类精度。由图4可知，PELM两个隐藏层的节点数分别达到180、120时，总体分类精度达到最优，当隐藏层节点数超过300时，总体分类精度出现下降的趋势，这是因为Indian pines数据集样本数较少，随着隐藏层节点数增加，网络结构复杂，出现了过拟合现象。

2)Pavia university数据集。表5、表6是各算法模型的对比实验结果，其中SVM核函数9选择linear；ELM隐藏层数为1层，节点数为1 500，激活函数为sigmoid；PELM的两个ELM网络结构隐藏层数都设置为1层，节点数为500，激活函数分别选择sigmoid和tanh；2D-CNN邻域大小选择9×9，epoch设为300；3D-CNN像素块大小选择9×9×30，epoch设为300。

表3 Indian数据集各算法分类精度对比 %

表4 India数据集各算法Kappa系数和运行时间

SSFCN-PELM模型在2D-CNN部分输入为35×35×10数据块，使用两个卷积层，卷积核数量分别设为10、30，大小设为3×3，学习率设为0.01，epoch设为50，1D-CNN部分使用两个卷积层，卷积核大小设置为5，数量为64，学习率设为0.01，epoch设为100。图5是模型在两个隐藏层不同节点数影响下的分类精度，由图5可知，PELM两个隐藏层节点数分别达到60、40时，总体分类精度达到99%以上，虽然随着隐藏层节点数增加模型总体分类精度仍在提升，但考虑时间因素和过拟合的情况，最终两个隐藏层节点数分别设为60、40。

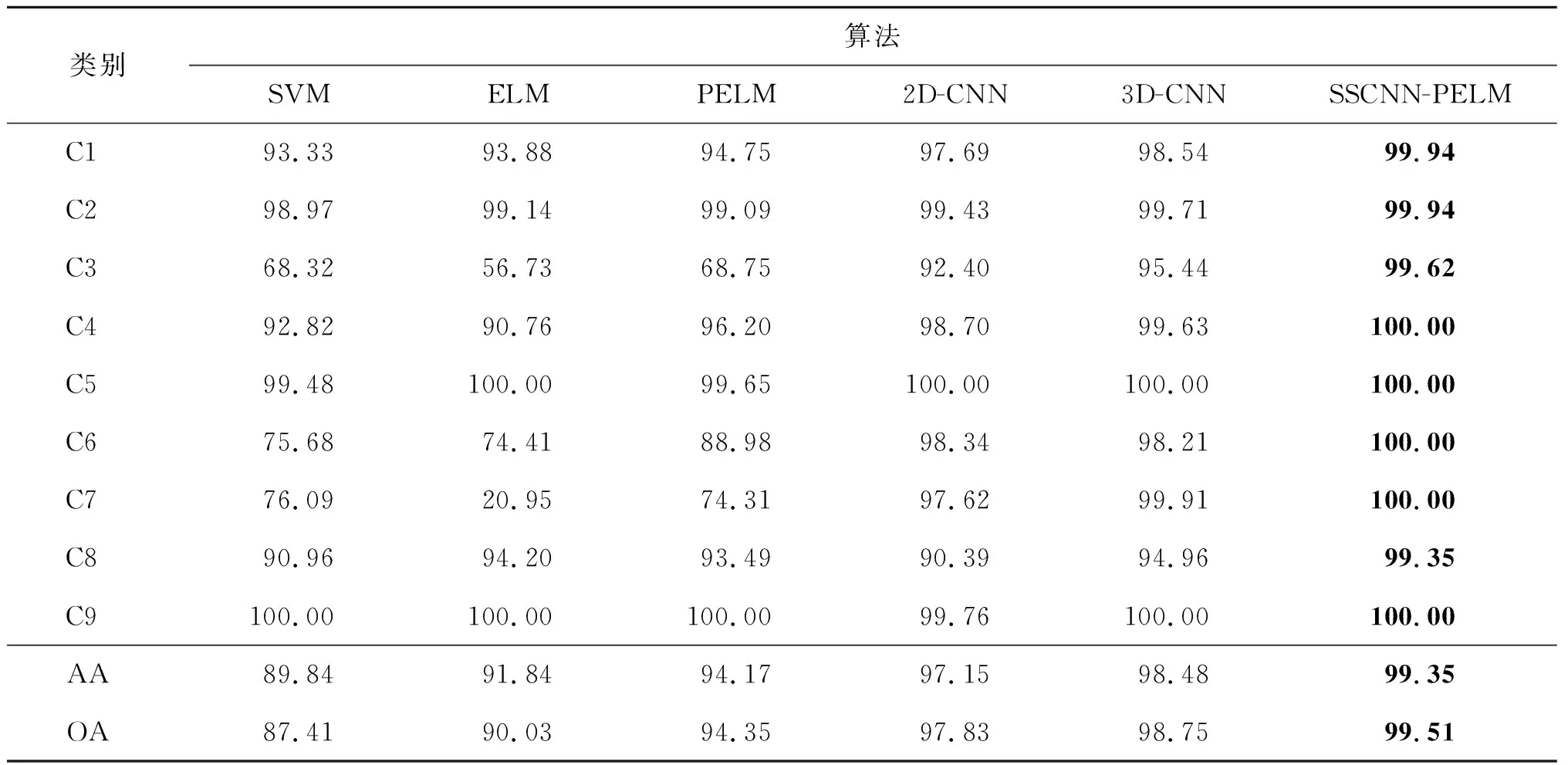
表5 Pavia university数据集各算法分类精度对比 %

表6 Pavia university数据集各算法Kappa系数和运行时间

3.3 实验结果与分析

从表3至表6可以得到以下结论。

1)所有对比算法中，ELM的分类速度最快、精度最低，尤其是在训练样本较少的情况，如Indian pines中C1、C3、C4，Pavia university数据集中C3、C7的分类精度在70%以下；PELM相比ELM在两个数据集中精度分别提升了5%和4%，相比SVM提升了2%和8%，分类时间相比SVM更短，测试集样本数越多，效果越明显，PELM在Pavia university数据集中的分类时间只有SVM的十分之一，在3种分类算法中效率最高。

2)SSCNN-PELM在 Indian pines数据集中有6类样本分类精度达到100%，Pavia university数据集中有5类样本分类精度达到100%，而且在分类时间上也有明显的优势。只有Indian pines数据集中C16的表现上弱于3D-CNN。图6和图7是各个对比实验的分类图，SVM、ELM、PELM完成高光谱图像分类会产生很多的椒盐噪声，而在2D-CNN、3D-CNN以及SSCNN-PELM中因为考虑了空间信息，分类效果更加平滑。

3)与3D-CNN相比，SSCNN-PELM在 Indian pines数据集中分类精度提升了2.26%，分类时间降低了94.50%；在Pavia university数据集中分类精度提升了0.77%，分类时间降低了91.31%。说明与常用深度学习方法相比，SSCNN-PELM具有更强的优越性。

4 结束语

本文针对高光谱图像的分类问题，结合SSCNN和PELM的优势，提出了新型的SSCNN-PELM模型。利用SSCNN提取高光谱图像的空间信息及深层光谱信息，将2D-CNN和1D-CNN输出特征输入PELM进行融合；利用PELM分类优势对空-谱信息进行分类。在Indian pines和Pavia university 两个数据集上进行实验验证，实验结果表明，SSCNN-PELM模型提高了高光谱图像的分类精度及速度，并在小样本训练条件下也能取得良好的效果。

在实验过程中发现，SSCNN-PELM模型虽然分类精度高，但是模型存在训练时间较长的问题，在后续的研究工作中可以尝试继续改进CNN模型，减少模型参数，以达到保证分类精度的同时降低训练时间的目的。