一种适用于双波段旋转相控阵雷达的目标跟踪方法

傅虹景，贾春宁，于守江，李冬宇，罗 静

(1.上海航天电子技术研究所，上海 201109；2.陆军装备部驻上海地区第三军事代表室，上海 201109)

0 引言

双波段旋转相控阵雷达采用方位机扫、俯仰相扫模式，具备搜索范围广、跟踪目标数量多的优点[1-2]。双波段旋转相控阵雷达相比于单波段雷达，拥有更丰富的频率资源、更强的抗干扰能力，且时间资源灵活，可以在同一时间调度不同波段的波束跟踪目标，从而提高目标的发现概率[3-4]。双波段旋转相控阵雷达2个波段对应的回波通道可以形成2个不同精度的点迹数据通道，若对2个通道的点迹数据分别进行跟踪滤波处理，不仅增加计算量，而且不能充分利用双波段雷达的点迹信息，使得跟踪精度较差[5-6]。

为解决上述问题，本文基于数据压缩处理技术提出了一种适用于双波段旋转相控阵雷达的目标跟踪方法。该方法首先在不同点迹通道中进行点迹凝聚，然后对2个通道的点迹数据进行点迹融合，以提高点迹数据的精度,降低后续航迹滤波处理的计算量，从而得到较好的目标跟踪结果。

1 雷达量测模型

假设在直角坐标系中，目标的离散运动状态方程可以表示为：

x(k+1)=F(k)x(k)+v(k)，

(1)

式中，x(k)为目标的状态向量，包括目标的位置、速度和加速度等状态信息：

(2)

F(k)为状态转移矩阵，表示目标状态的变化方式；v(k)为零均值、白色高斯过程噪声序列，其协方差为Q(k)[7]。

雷达对目标的量测值是在极坐标系下产生的，所以雷达的量测方程为非线性的，假设双波段旋转相控阵雷达中波段b对目标的量测方程可以表示为：

zb(k+1)=h[x(k+1)]+wb(k+1),

(3)

式中，zb(k+1)为波段b的量测值：

(4)

rb为量测点迹距离；ab为量测点迹方位角；eb为量测点迹俯仰角。h[·]为量测矩阵，表示雷达的观测方式：

(5)

wb(k+1)为零均值、白色高斯量测噪声序列，其协方差为Rb(k)：

(6)

2 数据压缩处理

双波段旋转相控阵雷达在一个调度周期内，可以调度不同波段的波束观测目标，且需要波束交叠来覆盖目标空域。因此存在相邻波束均能发现目标，形成目标点迹的现象，即各波段回波通道内存在多个点迹来源于同一目标，通道之间同样存在多个点迹来源于同一目标。若对这些来源于同一目标的点迹分别进行航迹滤波处理，会显著增加数据处理的计算量，难以满足实时处理的要求。本文提出的双波段旋转相控阵雷达点迹数据压缩处理流程示意如图1所示。

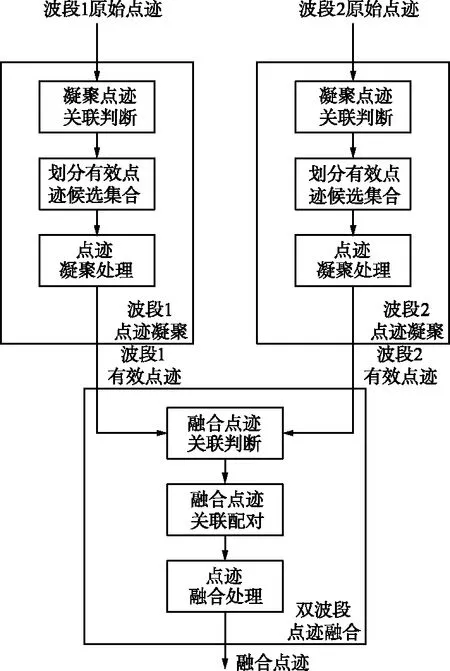
图1 双波段旋转相控阵雷达点迹数据压缩处理流程Fig.1 Schematic diagram of the data compression processing of dual-band rotating phased array radar

首先对各点迹数据通道内的点迹进行凝聚处理，再对不同点迹数据通道间的点迹进行融合处理，以此实现压缩点迹数据的目的，降低后续航迹滤波处理的计算量。

2.1 点迹凝聚

假设数据处理接收第k个调度周期波段b的点迹数据集合为：

(7)

式中，mk为点迹个数。

点迹凝聚的处理步骤如下：

① 凝聚点迹关联判断

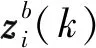
(8)

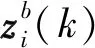
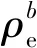
② 划分有效点迹候选集合

将第k个调度周期波段b的所有点迹依据连通情况划分有效点迹候选集合，假设第i个有效点迹候选集合为：

(9)

③ 点迹凝聚处理

有效点迹候选集合内的点迹满足连通条件，因此认为候选集合内的所有点迹均来源于同一目标。利用点迹的幅度信息凝聚加权可以得到有效点迹：

(10)

式中，Aj为第j个点迹的信号幅度[11]。

2.2 点迹融合

假设第k个调度周期波段b的有效点迹集合为：

(11)

点迹融合的处理步骤如下：

① 融合点迹关联判断

(12)

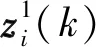
② 融合点迹关联配对

根据波段1有效点迹与波段2有效点迹的关联情况，对融合点迹关联配对。若波段1的有效点迹有多个波段2有效点迹与之相关联，则采用最近邻域法选择相距最近的点配对[13]。融合点迹关联集合为：

(13)

融合点迹关联集合中至多有2个有效点迹，且是源于不同点迹通道的。

③ 点迹融合处理

若融合点迹关联集合中仅有1个点迹，则无需做融合处理；若融合点迹关联集合中有2个点迹，则以点迹对应的测量误差作为权重进行融合处理，融合后的点迹为[14]：

(14)

融合后点迹的等效测量误差为[15]：

(15)

3 扩展卡尔曼滤波

雷达在极坐标系下的量测方程是非线性的，若将雷达量测值转换到直角坐标系下，则存在量测误差耦合的情况，会导致跟踪精度的降低[16]。扩展卡尔曼滤波通过泰勒级数展开，将非线性滤波问题转化为线性滤波问题，适用于极坐标系下的目标跟踪[17]。考虑目标跟踪算法的计算效率，本文采用一阶卡尔曼滤波算法对融合点迹进行处理，其流程如图2所示。

图2 扩展卡尔曼滤波算法流程Fig.2 Flowchart of extended Kalman filtering algorithm

具体步骤如下：

① 根据k时刻的估计值计算状态的一步预测：

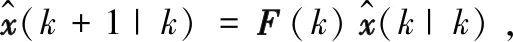
(16)

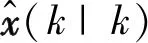
② 根据k时刻估计值的协方差计算协方差的一步预测：

P(k+1|k)=F(k)P(k|k)F′(k)+Q(k)。

(17)

同时，为降低扩展卡尔曼滤波过程中的线性化误差，采用标量因子φ>1对协方差预测矩阵进行加权：

P*(k+1|k)=φP(k+1|k)。

(18)

在后续滤波过程中，使用加权后的协方差预测矩阵迭代更新[18-19]。

③ 根据k+1时刻的状态预测值计算量测预测值：

(19)

④ 计算新息的协方差：

S(k+1)=hx(k+1)P*(k+1|k)h′x(k+1)+Rm(k+1)，

(20)

式中，hx(k+1)为向量h的雅克比矩阵，即：

(21)

式中，

(22)

(23)

Rm(k+1)为融合点迹等效测量误差的协方差矩阵：

(24)

⑤ 计算滤波增益：

K(k+1)=P*(k+1|k)h′x(k+1)S-1(k+1)。

(25)

⑥ 计算k+1时刻的新息：

(26)

⑦ 更新k+1时刻的目标状态的估计值：

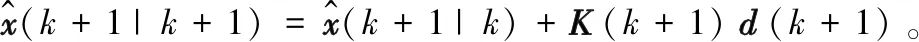
(27)

⑧ 更新k+1时刻的目标状态的协方差矩阵：

P(k+1|k+1)=P*(k+1|k)-

K(k+1)S(k+1)K′(k+1)。

(28)

以上是一次扩展卡尔曼滤波的完整过程，整个扩展卡尔曼滤波算法可以按照上述步骤递推完成。

4 仿真试验与结果分析

为验证本文所提目标跟踪方法的有效性，对双波段旋转相控阵雷达目标跟踪问题进行了仿真试验和分析。

目标运动场景：跟踪对象为三维空间中的单个目标，目标的起始位置状态为x(0)=[25 000 m,-150 m/s,0 m/s2,10 000 m,-100 m/s,0 m/s2,8 000 m,0 m/s,0 m/s2]，目标的运动方式为匀速运动，目标运动的过程噪声为零均值，方差为1 m/s2的高斯白噪声，目标的运动轨迹如图3所示。

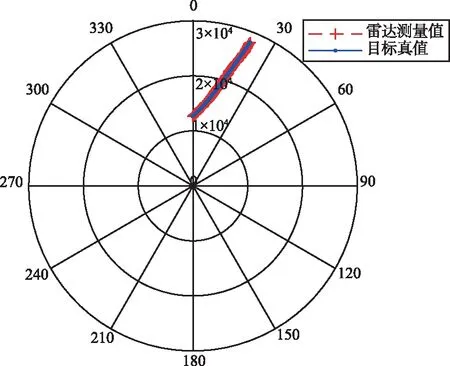
图3 目标运动轨迹Fig.3 Trajectory of target

雷达量测仿真参数：雷达波段1的距离量测噪声为零均值，标准差为60 m的高斯白噪声，方位和俯仰量测噪声均为零均值，标准差为0.4°的高斯白噪声，目标发现概率Pd=0.8；波段2的距离量测噪声为零均值，标准差为15 m的高斯白噪声，方位和俯仰量测噪声为零均值，标准差均为0.1°的高斯白噪声，目标发现概率Pd=0.9。雷达采样间隔均为T=1 s。仿真结果由100次蒙特卡罗实验统计得到。

采用不同方法对目标跟踪的误差曲线如图4～图6所示。不同方法性能比较结果如表1所示。

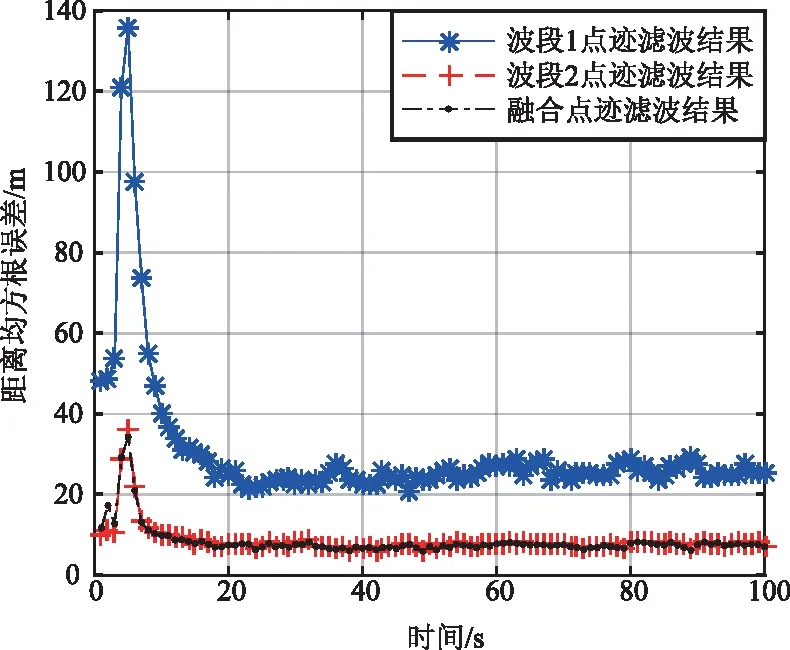
图4 目标距离均方根误差Fig.4 Root mean square error of target distance

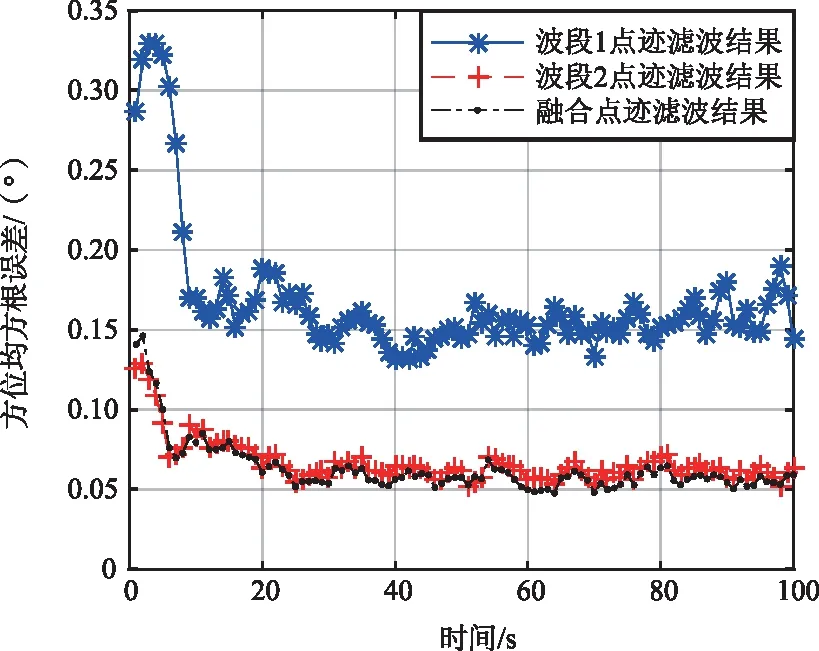
图5 目标方位均方根误差Fig.5 Root mean square error of target azimuth

图6 目标俯仰均方根误差Fig.6 Root mean square error of target elevation

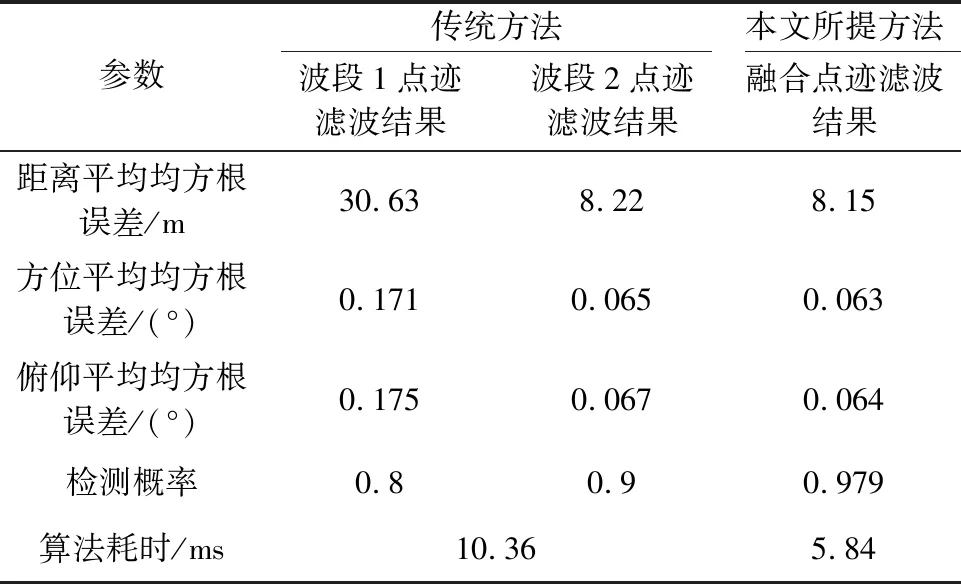
表1 不同算法性能对比

由图4～图6和表1可以看出，相较于各波段不同精度点迹分别滤波处理的传统方法，经过数据压缩处理后的融合点迹进行航迹滤波处理，其滤波误差更小，且提高了目标检测概率，减小了计算量。

5 结束语

本文详细介绍了一种双波段旋转相控阵雷达目标跟踪方法，该方法主要采用数据压缩处理技术，首先在各波段点迹通道内根据点迹的信号幅度进行凝聚处理，然后根据点迹测量误差的方差对2个通道的点迹数据进行融合处理，可以提高点迹数据精度，从而达到降低航迹滤波处理误差的目的。对比仿真结果发现，该方法相较于传统目标跟踪方法，跟踪误差结果更小，且降低了计算量，提高了目标检测概率。本文提出的双波段旋转相控阵雷达目标跟踪方法只考虑了雷达正常探测情况下的目标跟踪问题，针对雷达受干扰情况下的目标跟踪问题将是下一步需要研究的内容。