基于随机森林算法的地表点云孔洞修补

吕富强，唐诗华,2*，李灏杨，刘坤之

(1.桂林理工大学 测绘地理信息学院，广西 桂林 541004；2.广西空间信息与测绘重点实验室，广西 桂林 541004)

0 引言

使用无人机航测技术进行地表信息的获取，具有速度快、精度高、成本低以及灵活性强等特点，因此，无人机航测技术在测绘领域被普遍使用。但在进行点云数据的采集与处理过程中，会由于非目标地物遮挡、数据获取与处理技术的局限等各方面原因，造成点云数据的部分缺失，形成各种点云孔洞。这些孔洞的存在给后续测绘产品的生产带来较大的影响，在前期的处理工作中，需要对这些点云孔洞进行修补，以便后续的产品制作。

为了解决无人机获取的点的孔洞问题，王春香等[1]使用优化BP神经网络的方法进行点云孔洞的修补，该方法在密度均匀的点云孔洞修补中具有较好的效果，但在密度差异较大的点云孔洞修补中效果不够理想。刑鹏威等[2]使用LSSVM算法对点云孔洞进行修补，该方法总体的修补效果较好，但在局部的修补中会存在误差较大的问题。李永强等[3]通过地空雷达点云数据融合的方法对建筑物点云孔洞进行了修补，该方法修补的自动化程度较高，但需要进行地空数据的同时采集，数据获取成本较高，且在局部隐蔽区域的修补上效果还有待提高。Davis等[4]提出了基于体数据扩张的修补算法，该算法适应性较强，但在修补的精度上还有待提高。Chen等[5]将RBF函数进行曲面孔洞的修补，该方法在曲面较为平滑的区域修补精度较高，但在曲率变化较大的区域修补精度无法得到保证。这几种方法对孔洞面积较小、地势起伏平缓、特征缺失较少的地表点云孔洞修补效果较好，但在地形起伏较大、点云分布杂乱以及孔洞面积较大的地表区域中，修补效果还不够理想，修补结果的稳定性以及局部修补精度上还难以达到生产需求。因此，在无人机点云孔洞的修补中，需要一种适应性更强、精度更高的修补方法。

随机森林算法具有良好的泛化性与抗噪性，可以避免过度拟合，但目前随机森林多用于矿产[6-7]、大气[8]、变形监测[9-10]、土地利用[11]以及影像检测[12-14]等不同领域，还未运用到无人机点云的孔洞修补中。因此，本文提出了一种基于随机森林算法对地表点云孔洞进行修补的方法。根据随机森林算法良好的泛化性与抗噪性，对无人机获取的地表点云孔洞进行修补，并将该算法的修补结果与LSSVM和BP神经网络2种常用的修补算法进行修补结果的比较与分析。

1 随机森林算法原理

1.1 随机森林的定义

随机森林算法是一个依据决策树为学习器的分类方法，属于Bagging类型，采用分类回归树(Classification and Regression Tree，CART)决策树为弱学习器，对原始数据使用bootstrap重抽样的方法抽取出多个样本，在样本基础上构建决策树模型，根据多棵决策树的预测，经过投票或取均值的方式对所有分类器的结果进行统计，进而得出最终的预测结果[15]。

1.2 随机森林的预测模型

数据因变量为连续数值时，CART决策树算法则为回归树，叶子的观测均值为预测值，采用二分递归分割技术分裂。随机森林算法使用“基尼指数”划分属性的选择，其样本纯度用基尼值表示为：

(1)

式中，Gini为基尼值；K为样本类别数；Pk为所选样本属于k类别的概率；1-Pk为样本错分概率。基尼指数越大时，不确定性越大；基尼系数越小时，不确定性越小。

预测模型通过样本X和预测变量Y生成依赖于随机变量的回归树，关于k类别的样本数取均值即可得到预测模型[16]。从原始数据的n个样本中随机抽取多个独立样本构成训练样本，未被抽取的样本称为袋外数据。被抽中的样本集再随机抽取特征集，构建决策树。每颗二叉树从根节点开始按照节点不纯度最小原则，对训练样本集进行划分，各节点分裂至满足分支停止规则为止。进行数据预测时，使用均方误差(MSE)最小的特征来分裂节点：

(2)

该算法在特征选取时，从n个样本中随机选取，避免了数据的过度拟合，预测模型不会被特定组合所确定，抑制了模型的拟合能力。

2 实验与分析

2.1 数据来源

本文实验使用的是无人机获取的广西壮族自治区桂林市雁山区雁山街某区域的无人机点云数据。采用大疆精灵Phantom 4 RTK小型多旋翼高精度航测无人机获取数据，它具备厘米级导航定位系统和高性能成像系统。实验区域面积2 565.277 m2，存在较多的坑洼与土堆，且存在较多低矮植被，区域周边为施工用地。选取3处能代表地表特征的区域作为实验样本，设定为孔洞区域，3个孔洞区域分别分布于低矮植被区域、坑洼区域以及起伏较大的区域，具体位置如图1所示。

(a) 三维模型

(b) 正射影像图1 孔洞区域Fig.1 Hole area

2.2 实验过程

本文实验通过Matlab软件对点云孔洞进行修补。实验选取的3个孔洞区域的训练样本数分别为473，2 174，2 303个，检核点数分别为468，819，1 196个。

在参数的选择上，决策树的数量和决策树的节点个数为影响预测模型精度和稳定性的2个重要因素，根据文献[10]可知其选取原则如下：

mtry=[lbs]，

(3)

(4)

式中，mtry为决策树的节点个数；s为数据的变量个数。

将数据的训练集与测试集分别导入Matlab中，以点云数据中的平面坐标作为数据样本X的2个独立样本，以点位高程值作为预测变量Y，生成依赖随机变量θ的回归树，通过回归树进一步建立随机森林预测模型。

使用随机森林预测后，导出预测结果，将预测结果与孔洞周围点云数据进行汇总与展示，使用CloudCompare软件对缺失面积较大的孔洞进行修补前后的效果展示，如图2所示。

(a) 修补前

(b) 修补后

(c) 修补前剖面图

(d) 修补后剖面图图2 修补前后比对Fig.2 Comparison before and after repair

从图2可以看出，使用随机森林算法修补前后的变化明显，从修补前后的总体视图与修补前后的剖面视图可证明，该算法的修补结果连续性、平滑性较好，匹配度较高，具有较好的修补效果。

2.3 精度分析

为了验证随机森林算法修补结果的精确度、稳定性以及适用性，将随机森林的高程预测结果与BP神经网络、LSSVM算法的预测结果进行对比。实验从3组数据修补结果的残差、平均绝对误差(MAE)、MSE和均方根误差(RMSE)4个方面进行修补结果的精度对比与分析。

从3个孔洞中分别选取修补结果中的200个点进行残差曲线的绘制，如图3所示。

根据3种算法分别对3个孔洞修补得到残差曲线图，可以看出LSSVM算法在点云缺失面积较小的孔洞中，残差值总体较小，但在点云缺失面积较大的孔洞中，其残差值总体较大，预测结果不稳定。BP神经网络在面积较大的孔洞修补中，仍具适用性，但其算法的稳定性不足，容易出现过度拟合的现象。随机森林算法在3个孔洞的修补结果中，稳定性最强，残差曲线总体平稳于另外2组算法。残差值总体较小，精度最高。由此可以得出，随机森林算法在点云缺失面积较大或地形变化复杂的孔洞中更具适用性，算法稳定度更强，且具有更高的修补精度。

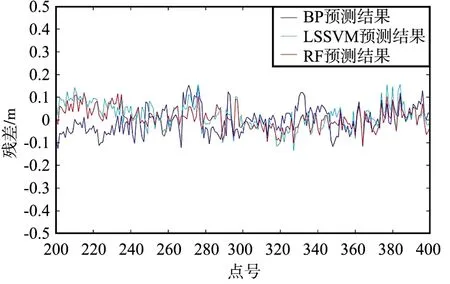
(a) 孔洞1

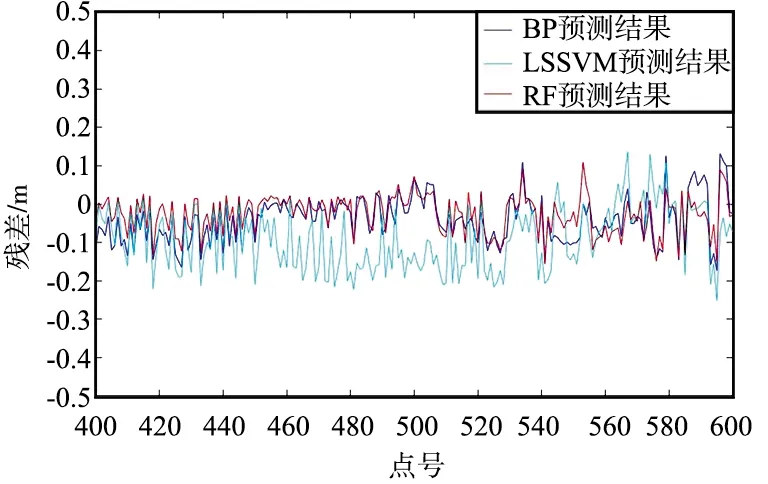
(b) 孔洞2

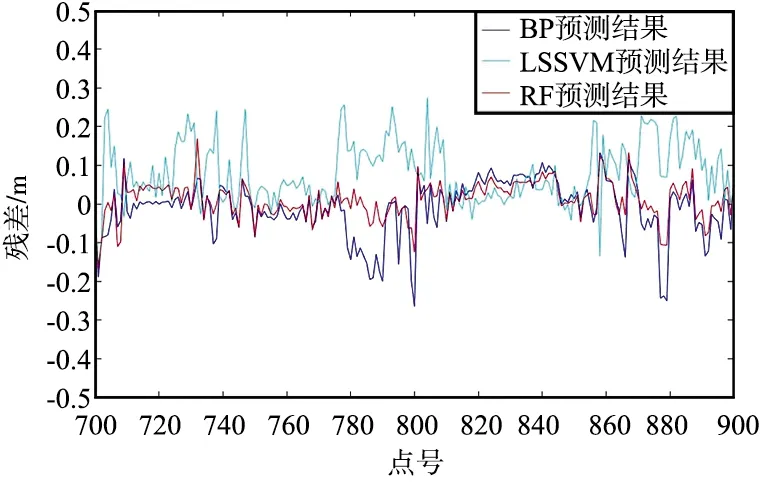
(c) 孔洞3图3 残差曲线Fig.3 Residual curve

为了进一步验证随机森林算法的适用性与算法精确性，将3种算法修补结果的MAE，MSE和RMSE进行对比与分析[18]。计算如下：

(5)

(6)

(7)

式中，y′为预测值；yi为原始值；n为训练样本数量[19]。MAE，MSE，RMSE的计算结果如表1所示。

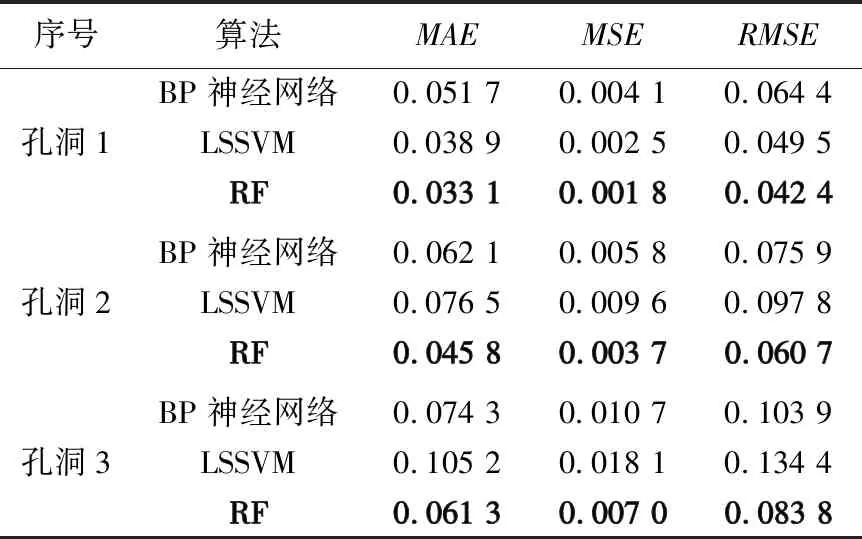
表1 精度比较

由表1可以看出，随机森林算法的MAE，MSE和RMSE均小于BP神经网络与LSSVM算法，3组算法总体精度均满足1∶500地形图航空摄影测量规范要求，但在部分点的修补精度上，BP神经网络与LSSVM算法存在误差较大的情况，而随机森林算法在局部点的修补精度上仍满足精度要求。在3组数据中，BP神经网络的MAE值最大为0.074 3 m，LSSVM算法的MAE值为0.105 2 m，而随机森林算法的MAE值最大仅有0.061 3 m，最小值为0.033 1 m，明显小于前2种算法。RMSE的对比中，BP神经网络与LSSVM算法的最大值分别为0.103 9，0.134 4 m，而随机森林算法的最大值为0.083 8 m，最小值为0.042 4 m，明显小于另外2种算法。

由以上残差与精度的对比与分析可得出，随机森林算法的修补精度高于BP神经网络和LSSVM两种算法，且在点云缺失面积较大的孔洞区域的修补中，仍具有较好的修补效果，说明随机森林算法相比于另外2种算法的适用性更强，并且该算法具有更强的稳定性和抗噪性。

3 结束语

本文针对无人机航测数据中的点云孔洞问题，提出了基于随机森林算法的点云孔洞修补方法，随机森林的预测模型具有较高的预测精度，具有一定的抗噪性，且不容易出现过度拟合。在修补效果上，随机森林算法的修补结果连续性、平滑性较好，匹配度较高，具有较好的修补效果。在精度上，随机森林算法与BP神经网络、LSSVM算法的MAE，MSE，RMSE的对比中，随机森林算法的各误差均小于另外2种算法，证明了使用随机森林算法的孔洞修补方法在地表还原与高精度DEM生产的可行性，精度上满足1∶500地形图航空摄影测量规范。在复杂地形或点云孔洞面积较大的地形中，随机森林算法相比于BP神经网络、LSSVM算法的修补精度更高，稳定性与适用性更强，是一种可行的点云孔洞修补方法。该算法也存在一些不足，当决策树数量较多时，算法的训练时间会加长，使得模型预测效率降低。在后续的工作中，将对此进行下一步的研究。