利用信号变换域的深度学习调制识别算法

廖 星，高 勇

(四川大学 电子信息学院，四川 成都610065)

0 引言

通信信号调制识别技术在各种领域占据了重要的位置。在民用领域，通信信号管理、信号干扰识别、信号监控和认知无线电是通信信号识别技术的主要应用场景[1]。自动调制识别(Automatic Modulation Recognition，AMR)技术可以在先验信息不足的情况下，实现对信号的自动识别和处理。

传统的调制识别方法由于所需先验知识较多，且在低信噪比下识别率较低使得应用受到限制[2-4]。近年来，人工智能和神经网络成为了热门的研究方向，并且被应用到越来越多的领域。例如自然语言处理、计算机视觉和语音识别[5]等方面，各种各样的新型算法不断被提出，广泛应用于实际生活中。神经网络方法通过反向传播实现算法参数的自动调整，更能适应新型调制方式的出现以及复杂调制方式的识别。随着多种网络结构的提出，研究者们逐渐地将不同的网络结构应用于AMR，如循环神经网络[6-7](Recurrent Neural Network，RNN)及其结构变种长短时记忆网络(Long Short-Term Memory，LSTM)[8-9]、卷积神经网络(Convolution Neural Network，CNN)[10-11]和生成对抗网络(Generative Adversarial Networks，GAN)[12-13]等。Yang等[14]提出，通过连续小波变换将调制信号转换为二维时频图，并将其作为AlexNet网络的输入，对于集内8种信号(2ASK，4ASK，2PSK，4PSK，2FSK，4FSK，6QAM和64QAM)，实现了低信噪比下对信号的识别，然而在10 dB时，才有较高的识别率。张军等[15]将信号的IQ分量并联后，送入到CLDNN(Convolutional，Long Short Term Memory，Fully Connected Deep Neural Networks)中进行分类识别，使用开源数据集RML2016.10a，在0 dB下，集内信号的平均识别率约为84%。文献[16]通过改进残差神经网络，将在Matlab仿真下产生的信号集(BPSK，4PSK，8PSK，4QAM，16QAM，64QAM，4PAM，8PAM八种信号)直接送入到改进的网络中，在信噪比为10 dB时，才能达到95%的识别率。文献[17]提出了一种结合一维卷积和LSTM的深度学习模型，将开源数据集RML2016.10b内信号的幅度和相位作为网络的输入进行识别，在低信噪比下有较高的识别率，但最高识别率仅为95%左右。文献[18]将信号的IQ分量作为卷积神经网络的输入，再级联双向LSTM进行分类识别，对于开源数据集RML2016.10a，在-10～20 dB范围内平均识别率均未超过90%。

将原始信号作为网络输入进行识别，不足以反映出信号的特征，识别率较低。本文基于并联网络和特征融合的思想，对信号进行不同的变换，并将变换后的特征向量作为并联网络的输入。离散余弦变换在图像处理领域被广泛应用，而在调制识别领域较少使用，其频谱对信号能量有高度的聚集作用。本文先对信号进行离散余弦变换，同时对其进行自相关处理，得到不同变换域下的信号信息，分别将其送入到并联网络。受残差网络的启发，对一般残差模块进行改进，2路网络均用改进后的残差网络，且因为2路特征输入的维度一样，所以残差网络结构也相同。最后，将并联网络提取到的特征拼接起来，进行softmax分类。结果表明，本文所提出的结合信号不同变换域下特征的算法在低信噪比下对MPSK和MQAM信号有较高的识别率。

1 信号模型

本文所用到的MQAM信号主要包括16QAM，32QAM，64QAM和128QAM。MQAM的基带信号波形表达式为：

(1)

式中，An为调制信号第n个符号的振幅；Sn表示发送端发送的第n个符号；g(t)为脉冲成形函数；Tb为符号周期；fc和θn分别表示第n个符号的载波频率和载波相位。

相移键控MPSK信号通过载波相位变化来传递数字信息，振幅保持不变。本文所用到的MPSK信号主要包括BPSK，QPSK和8PSK。MPSK的基带信号波形可以表示为：

(2)

式中，K=1,2,…,M,M=2k。

调制信号经加性高斯白噪声信道(AWGN)后，接收端的信号为：

x(t)=s(t)+n(t)，

(3)

式中，s(t)为调制信号；n(t)为均值为零的高斯白噪声。

2 信号预处理及网络结构

在实际的无线通信中，信道环境复杂，存在频偏、相偏、未知码速率和难以准确估计信噪比等问题。直接将接收到的信号作为神经网络的输入进行识别，难以提取到信号更多的特征，识别率较低。考虑到信号在不同的变换域中所表现的信号特征不同，且不同的信号在同一变换域中的表现也不同。为了弥补单一变换的缺陷，提出了基于自相关和DCT两种变换的方式来表征信号，通过神经网络提取不同特征，融合拼接后进行信号调制方式识别分类。

2.1 自相关

自相关表达了信号在同一过程不同时刻的相互依赖关系，且信号和噪声以及噪声和噪声之间相互独立，故信号的自相关处理不仅能反映信号本身的特性，还能减少在自相关变换中噪声的影响，是一种较好的预处理方式。

自相关函数的表达式为：

R(τ)=E[x(t)x(t+τ)]。

(4)

将式(3)中x(t)的表达式代入式(4)可得：

R(τ)=E[(s(t)+n(t))(s(t+τ)n(t+τ))]=

Rss(τ)+Rns(τ)+Rsn(τ)+Rnn(τ),

(5)

式中，Rss(τ)为信号的自相关函数；Rsn(τ)和Rns(τ)分别为信号与噪声以及噪声与信号的互相关函数；Rnn(τ)为噪声的自相关函数。由于信号和噪声以及噪声和噪声相互独立，互不相关，故在τ不等于0时，有Rsn(τ)≈Rns(τ)≈Rnn(τ)≈0，R(τ)≈Rss(τ)。

2.2 离散余弦变换

傅里叶变换表明，任何信号都能表示为多个不同振幅和频率的正弦或者余弦信号的叠加。如果采用的是余弦函数，则信号分解过程称为余弦变换；若输入信号是离散的，则称之为离散余弦变换。DCT变换是对实信号定义的一种变换，变换后在频域中得到的同样为实信号，相比离散傅里叶变换(Discrete Fourier Transform，DFT)，DCT可以减少一半以上的计算。DCT变换主要运用于数据或图像的压缩，对于信号序列而言，则有信号谱分量丰富、能量集中的作用。DCT变换的公式为：

(6)

(7)

式中，X(k)是DCT变换矩阵；x(n)是N个有限值的一维实数信号序列，n=0,1,…,N-1；α(k)为补偿系数，k=0,1,…,N-1，使DCT变换矩阵变为正交矩阵。

2.3 网络结构

本文所用网络模型为改进后的残差网络。以一般残差模块(Residual Block)结构为基础，如图1(a)所示，输入和输出恒等连接，本文在连接部分进行了修改，为了同时提取不同维度的特征，使用不同大小卷积核的卷积层，再进行连接，改进后的残差模块如图1(b)所示。

(a) 一般残差模块

(b) 改进后的残差模块

实验采取并联网络的形式，将信号的自相关域和DCT域作为神经网络的输入。相比传统的决策树分类器，神经网络的识别分类效果更好，尤其是在低信噪比下的识别。具体网络结构如图2所示。本文所用RES_NET网络结构为左右2路，输入均为2×200的矩阵，第1个支路表示IQ信号经过自相关变换后的实部和虚部并联信号，第2个支路为IQ信号经过DCT变换后的实部和虚部并联信号；输出为1×7的向量，表示每类信号的识别准确率。特征融合层拼接2路网络所提取的不同特征。为减小过拟合，使用Dropout，并设值为0.5；且在每个卷积层后面添加Batch Normalization(BN)层进行批标准化，同时设置早停机制，以验证集损失值为监测指标，当该指标经过20个epoch未下降时，则停止训练。网络中，除最后一个Dense层外，所使用的激活函数均为LeakyReLU。与ReLU的不同之处在于负轴保留了非负常数d，也称为泄露值(依据经验值可选取0.1～0.5的数，经过多次实验，最终设为0.25)，使得输入信息小于0时，信息没有完全丢掉，进行了相应的保留，减少了静默神经元的出现。常用激活函数ReLU和本文所用激活函数LeakyReLU的对比如图3所示，其中，图3(a)为ReLU，图3(b)为LeakyReLu，可以看到二者的区别主要在负半轴。

(a) 激活函数ReLU

(b) 激活函数LeakyReLU(d=0.25)图3 ReLU和LeakyReLU的对比图Fig.3 Comparison of ReLU and LeakyReLU

3 算法仿真及性能分析

3.1 实验数据与环境

本次实验使用NI USRP-2930软件无线电设备采集实测数据。待识别的信号集包括BPSK，QPSK，8PSK，16QAM，32QAM，64QAM和128QAM七种调制信号，其中高阶QAM较难识别以及QAM类内信号不易区分。载频为915 MHz，码速率为500 kb/s，成型滤波器系数为0.35，采样率为2 MHz。每种调制信号均含38 000个样本，每个样本长度为200个I，Q采样点。训练集添加的高斯噪声是-10～20 dB的随机带内噪声[19]。测试集信号与训练集信号独立采集，每种调制信号在-10～20 dB范围内，每隔2 dB采集1 000个样本，共16 000个样本，样本长度仍为200，其他参数与训练集一致。

实验环境：显卡为NVIDIA RTX 3090，处理器为Intel Core i7-8700型CPU，内存为16 GB。基于tensorflow 2.2.4和keras 2.6.0框架搭建网络并完成测试分析工作，开发语言为Python3.7。

3.2 实验结果分析

设NUMall为7种调制信号的样本总数，NUMright为识别分类正确的样本总数，则平均识别率定义为：

(8)

7种信号分别在本文预处理和使用原始IQ数据的平均识别率-信噪比(SNR)曲线如图4所示。由图4可知，平均识别率随着信噪比的增强而提高。在本文的预处理方法下，当信噪比为0 dB时，平均识别率接近93%，相较于无预处理条件下的平均识别率，提高了接近45%。

图4 不同信噪比下的平均识别率Fig.4 Average recognition rate under different SNR

7种调制信号分别在不同信噪比下的识别率如图5所示。由图5可知，当信噪比为0 dB时，除QPSK外，其余6种信号的识别率均达90%以上;当信噪比为1 dB时，各类信号的识别率都达90%以上。

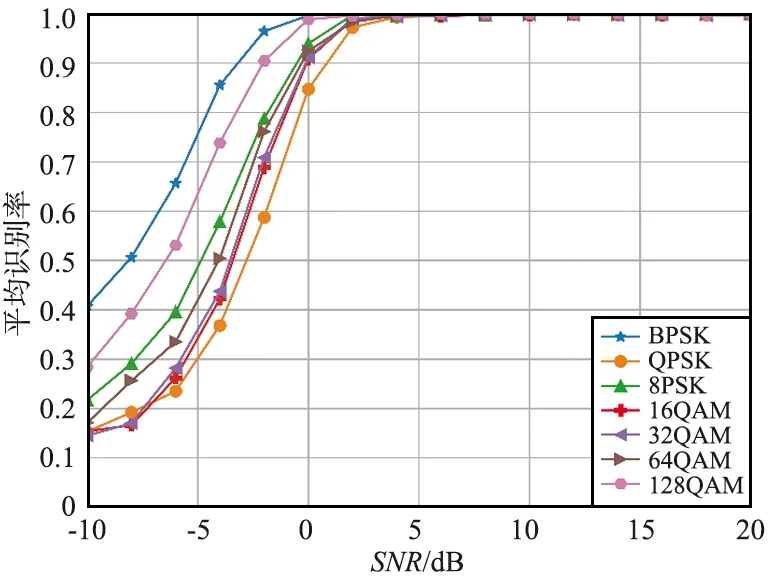
图5 各类调制信号在不同信噪比下的识别率Fig.5 Recognition rate of various modulation signals under different SNR

当信噪比为0 dB时，7类信号识别率的混淆矩阵如图6所示，显示了每类信号样本具体的分类结果，空白部分表示本次测试中错分率几乎为0。由图6可知，0 dB下，除QPSK有少量错分样本外，其余各类信号错分率较低。其中，BPSK信号和128QAM信号基本完全识别出。

图6 SNR = 0 dB时识别准确率的混淆矩阵Fig.6 Confusion matrix of recognition accuracy when SNR=0 dB

3.3 不同网络参数的性能对比

3.3.1 卷积层层数对识别性能的影响

卷积层的个数过少则提取不出信号的深层特征，过多则提升了网络的复杂度，容易出现过拟合。实验中，在固定第一个为改进后的残差块后(卷积核大小为1×3，1×3和2×5，数目均为64，结构如图2所示)，逐一增加卷积层，增加的卷积层卷积核大小为1×5，数目为64，在实验环境相同的条件下进行模型的训练及测试集的分类。计算不同卷积层数下的正确识别率以及分类时间，如表1所示。由表1可知，当在残差块后添加一层卷积层时具有最高的识别率和最短的分类时间。随着卷积层数的增加，网络的性能下降，当卷积层为一层时，网络能充分地提取出信号的特征，继续增加卷积层会增加冗余且增加模型的复杂度。故在后面的实验中，设置网络结构为一个残差块和一层卷积层。

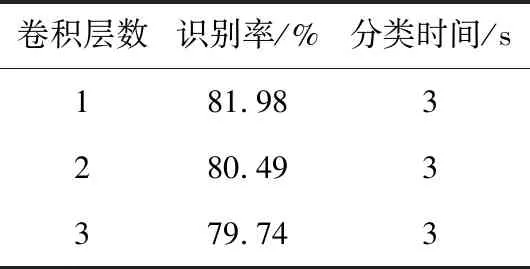
表1 不同卷积层数对识别性能的影响

3.3.2 卷积核对识别性能的影响

在固定上述网络结构的同时，改变卷积核的个数，对比得到最优的卷积核个数。实验分别设卷积核个数为32，64，128，256，其他参数保持不变。不同卷积核个数对识别率的影响如表2所示，可以得知，当卷积核个数为64时，识别效果最好。

表2 不同卷积核个数对识别性能的影响

卷积核尺寸的不同能提取不同程度上的信号特征，尺寸过大会忽略一些空间信息，过小又不能提取关键的特征。由于输入的维度是2×200，为了提取其高维特征，设残差块中的卷积核大小为2×n，skip连接部分的2个卷积层卷积核大小均固定为1×3，残差块后卷积层的卷积核大小设为1×n。设n的取值分别为3，5，7，不同尺寸的卷积核对识别性能的影响如表3所示。从表3中可以得知，选用2×5+1×5的卷积核时识别性能最佳。

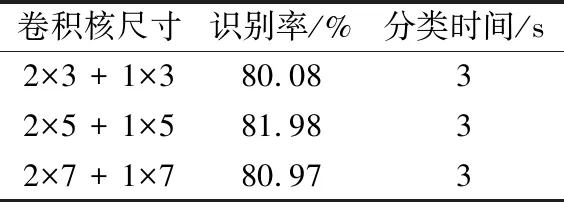
表3 不同卷积核尺寸对识别性能的影响

3.4 不同预处理方法性能对比

为了评估本文提出的结合信号多种变换域的预处理方法性能，在使用相同数据集、网络结构和实验环境的条件下，和单一变换即仅做DCT或仅做自相关变换处理对比。对比结果如图7所示。由图7可知，当信噪比为0 dB时，2种变换结合的平均识别率相较于单独的自相关和单独的DCT变换分别提高了约4%和5%，进一步说明了多种变换结合所能表现的信号特征更为丰富，识别效果更好。

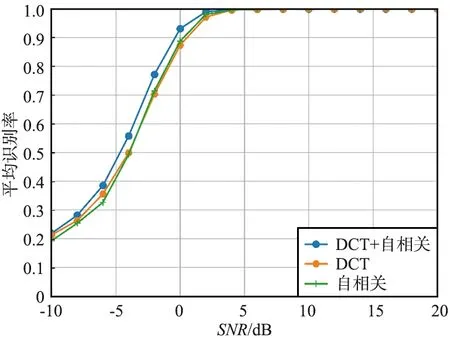
图7 不同预处理下的平均识别率Fig.7 Average recognition rate under different preprocessing

3.5 不同算法性能对比

为了进一步验证本文算法的优越性，在使用相同数据集的条件下，将本文算法与文献[10-13]提出的算法相比较，实验对比结果如图8所示。由图8可以看出，本文算法的信号平均识别率高于所对比的几篇文献的算法。

图8 不同算法下的平均识别率Fig.8 Average recognition rate under different algorithms

4 结束语

为了提高低信噪比下的MQAM和MPSK信号的识别率，提出了基于信号变换域的神经网络调制识别算法，即结合信号的自相关变换和离散余弦变换，将预处理后的信号作为实验搭建的并联网络的输入，最后拼接2路网络提取到的不同特征进行识别分类。实验结果表明，提出的预处理办法能在低信噪比下对BPSK，QPSK，8PSK，16QAM，32QAM，64QAM，128QAM这7类调制信号有较高的识别率。当信噪比达到1 dB时，每类信号的识别率均在90%以上，算法预处理简单，避免了繁琐的人工提取特征的过程，经过了实测信号验证，具有一定的实用价值。本文考虑的信道环境仅为高斯信道，实际应用中信道的环境更为复杂，多径效应明显，故接下来将考虑在多径信道下对信号的调制识别。