基于TC-CNN网络的残缺TACAN空/地信号识别方法

郝彦超，侯 进，杨宗源，王祥宇 ，李天宇 ,文志龙

(1.西南交通大学 信息科学与技术学院 智能感知智慧运维实验室，四川 成都 611756；2.西南交通大学 综合交通大数据应用技术国家工程实验室，四川 成都 611756;3.西南交通大学 唐山研究院，河北 唐山 063000)

0 引言

TACAN导航系统作为军用领域的传统通信手段，在全世界都有着十分广泛的应用。TACAN导航系统主要包括空/空、空/地2种模式，其中空/空模式用于空中设备间的通信，空/地模式用于空地设备间的通信，因此在对TACAN信号的侦收处理过程中，对TACAN空/地信号进行识别有着十分重要的军事意义[1-2]。

传统TACAN空/地信号识别的方法主要包括以下几种方案：一种是基于数字化的译码识别[3]，该方法主要是通过FPGA可编程逻辑器件的使用，对信号进行了数字化处理，针对TACAN空/地信号的脉冲类型、调制方式和不同脉冲群的周期等特点进行识别；另一种是通过使用模板匹配的方法[4-5]进行识别，该方法通过匹配TACAN空/地信号的脉冲数量、脉冲宽度等信号特征完成对信号的判断。上述2种方法都是以TACAN空/地信号的脉冲群特征作为判断条件，虽然能够检测出完整周期的TACAN空/地信号，但是当信号发生缺失时，信号部分特征(各个脉冲群数量、脉冲群个数等)不再完整，上述2种方法的识别率将会受到严重影响。

为解决因TACAN空/地信号缺失导致的识别率较低的问题。本文设计了一种基于CNN的新型神经网络模型方法，并利用该模型对残缺的TACAN空/地信号进行识别。经验证，该模型与传统模板匹配算法相比，在信号处于较低信噪比且信号残缺度较高的情况下，也能使信号的识别精度得到有效的提升。

1 TC-CNN模型

TC-CNN基于传统的CNN模型进行设计，CNN模型在数据分类和预测问题上比传统算法有着更高的效率和准确度，能够全面地捕捉TACAN空/地信号的关键特征。该模型的基本思想是通过TACAN空/地信号产生的IQ数据，分别对I路和Q路2组信号进行特征提取，同时，2组信号中的每一个数据都作为模型输入的特征点传递给后续的卷积层，之后通过模型中的连接层对I，Q信号进行特征融合，并使用多个隐藏层实现关键特征的提取。通过模型的多次迭代学习，计算出TACAN空/地信号中关键特征的权值，最后通过输出层输出2类侦收信号的识别概率，并选择最大概率作为最终结果，实现残缺TACAN侦收信号的识别。

1.1 构建TACAN空/地数据集

原始TACAN空/地信号采用了高斯脉冲调制技术[13-14]，以脉冲对的形式进行编码实现。在空/地X模式下，TACAN空/地信号一秒由3 600对脉冲组成，其中包括900对方位基准脉冲及由识别信号脉冲对、距离应答脉冲和随机填充脉冲对组成的2 700对其他脉冲。在空/地Y模式下，TACAN空/地信号一秒由7 155个脉冲构成，其中1 755个是方位基准脉冲群。剩余的2 700对由识别信号脉冲对、距离应答脉冲及随机填充脉冲等多种脉冲构成。TACAN空/地X信号和空/地Y信号的最大区别在于TACAN空/地信号的主基准脉冲群和辅助基准脉冲群的构成方式不同，TACAN空/地X信号的主基准脉冲群共由12个脉冲对组成，辅助基准脉冲群共由6个脉冲对组成，其中主基准脉冲群的脉冲间隔为(12±0.1)μs，脉冲对间隔为(30±0.1)μs；辅助基准脉冲群的脉冲间隔为(12±0.1)μs，脉冲对间隔为(24±0.1)μs。对于TACAN空/地Y信号，其主基准脉冲群共由13个单脉冲组成，辅助基准脉冲群也由13个单脉冲组成，其中主基准脉冲间隔为(30±0.1)μs，辅助基准脉冲群的脉冲间隔为(15±0.1)μs。上述特征是传统模板匹配法的识别关键。在本文实验中，所有TACAN空/地模式信号均来自SIMULINK工具包[15]所产生的带噪信号数据。本文根据上述TACAN空/地模式下的信号特征，对空/地模式下的2类信号进行了仿真实现。

根据TACAN空/地信号的产生条件[16-18]，设置信号的采样频率为51.2 MHz，中心频率为1 GHz，信号强度为-65 dBm，同时在信噪比分别为-3，0，3 dB的条件下，空/地X和空/地Y模式分别产生了900个信号，其中，各组信号分别以10%，20%，30%的丢失比例构造数据集。信号的产生参数设置具体如表1所示。根据参数设置，最终生成的各类型TACAN空/地信号数量如表2所示，其中，每种信噪比下的不同丢失比例的信号数量均为300个。

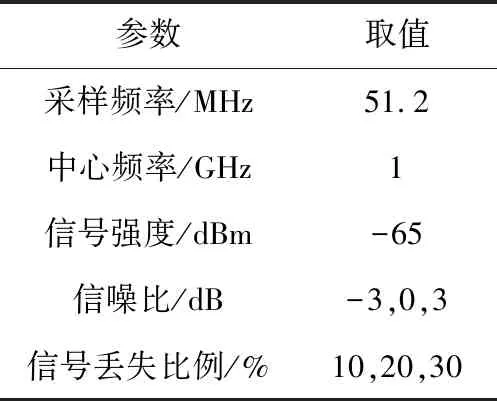
表1 TACAN空/地模式下的数据集参数

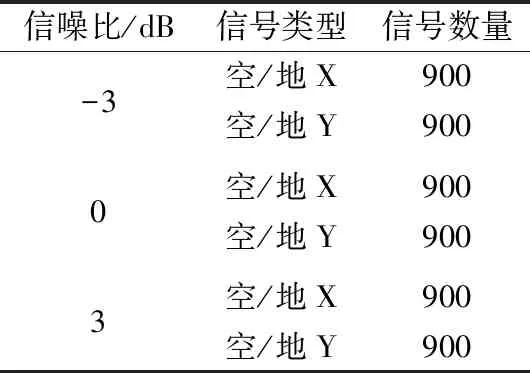
表2 TACAN空/地模式下的各类信号数量

完成上述工作后，将数据集以7∶2∶1的比例划分为训练集、验证集和测试集，同时在输入模型之前，使用随机脉冲信号对残缺的TACAN空/地信号进行补全处理，以保证数据长度的一致性。

1.2 TC-CNN模型设计

TC-CNN模型以多层CNN模型为基础，分别对TACAN空/地模式下的实部信号和虚部信号进行特征提取，并使用连接层进行特征融合，之后，再通过使用多个隐藏层进行二次特征提取，其中有一个重要的隐藏层——LSTM层[11]，该层的作用主要是提高TC-DNN模型对TACAN空/地信号时序性特征的学习能力，并最终通过输出层输出模型的分类结果。该模型的主要结构如图1所示。

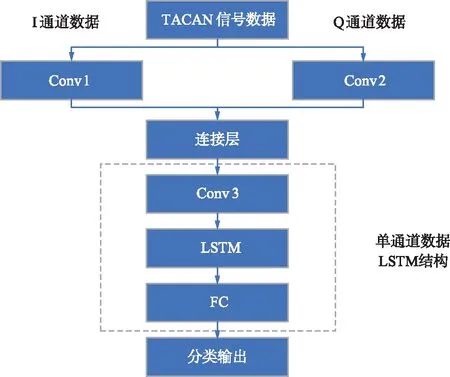
图1 TC-CNN模型结构Fig.1 TC-CNN model structure diagram

构建完成上述模型后，选择使用交叉熵损失函数作为该模型的损失函数，由于该模型是二分类模型，因此该损失函数的形式如下：

L=-[ylbp+(1-y)lb(1-p)]，

(1)

式中，y为TACAN空/地信号的真实标签；p为该样本经过模型预测之后分类为y的概率。也可以将该函数写为：

由于核心网网元之间的接口所涉及的链路，均通过核心网CE进行互联，对移动互联网的链路只需采集核心网CE与各个网元之间的链路，集采系统建议设置在核心网CE侧，如下图：

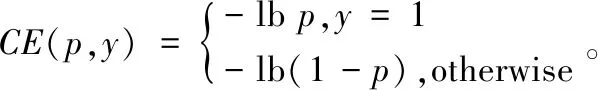
(2)

为了表示简便，最终用p空/地X表示样本属于空/地X信号的概率，最终该模型的交叉熵损失函数可以表示为：

CE(p,y)=CE(P空/地X)=-lb(P空/地X)。

(3)

2 实验

2.1 TC-CNN模型训练

在TC-CNN模型的训练过程中，选择AdamOptimizer[12]作为该模型的训练优化器，设置模型训练的epoch为50，学习率参数为0.000 1，学习衰减率decay为0.000 01。同时，模型中加入Dropout层来防止模型发生过拟合，训练开始后，Dropout层在模型训练时随机关闭的神经单元比例个数设置为0.5，测试时设置为1.0。为了能够使模型达到最优性能，模型中加入提前终止训练操作，当模型在5个epoch范围内不再上升或下降时，提前终止训练，这样能够使模型在停止训练时达到最优性能。最终，不同分类下各个模型的训练结果如图2～图4所示。

图2 信噪比为-3 dB时不同残缺率下模型训练结果Fig.2 Model training results under different defect rates when the signal-to-noise ratio is -3 dB

图3 信噪比为0 dB时不同残缺率下模型训练结果Fig.3 Model training results under different defect rates when the signal-to-noise ratio is 0 dB

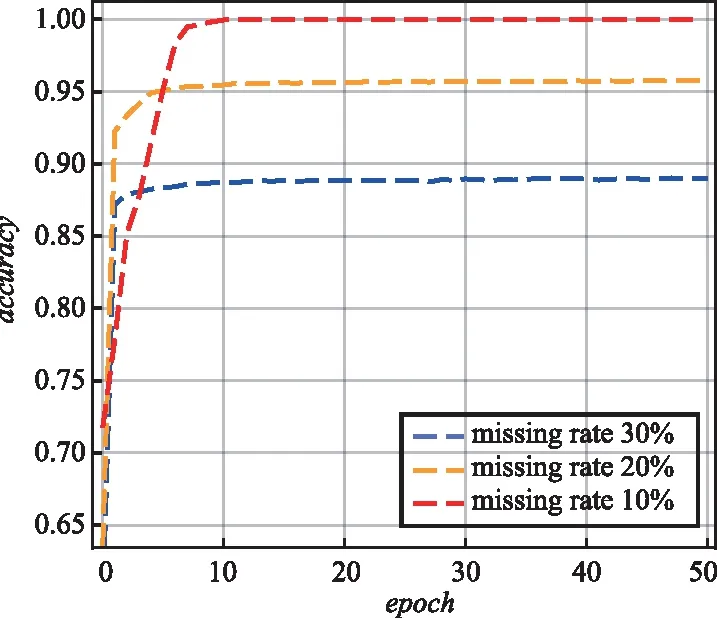
图4 信噪比为3 dB时不同残缺率下模型训练结果Fig.4 Model training results under different defect rates when the signal-to-noise ratio is 3 dB

由图2～图4可以看出，不同信噪比下，各模型方法均已收敛，当信噪比为-3 dB，信号残缺率为30%时，模型的准确率稳定在84%左右；信号残缺率为20%时，模型的准确率稳定在92%左右；信号残缺率为10%时，模型的准确率稳定在97%左右。当信噪比为0 dB，信号残缺率为30%时，模型的准确率稳定在86%左右；信号残缺率为20%时，模型的准确率稳定在95%左右；信号残缺率为10%时，模型的准确率稳定在99%左右。当信噪比为3 dB，信号残缺率为30%时，模型的准确率稳定在89%左右；信号残缺率为20%时，模型的准确率稳定在96%左右；信号残缺率为10%时，模型的准确率稳定在99.8%左右。在各残缺率下，模型的识别准确率随着信噪比的提升而渐次升高。但是当信噪比高于0 dB且信号残缺率低于10%时，模型的提升性能有限，这是因为当信号残缺率低于10%时，TACAN空/地信号中的各脉冲群信号较为完整，残缺的部分以随机脉冲为主。随机脉冲对模型最终的分类结果影响较小，因此当信号的信噪比高于0 dB且信号残缺率低于10%时，几乎可以忽略信号残缺率对模型造成的影响。

由该模型的训练结果也可以看出，信噪比保持一致的前提下，信号残缺率越低，模型准确率越高。这是因为对于TC-CNN模型，信号越完整，模型可学习到的特征越多，尤其是作为区分TACAN空/地信号的关键特征，主基准脉冲群和辅助基准脉冲群。因此当信号残缺率下降时，TC-CNN模型能够有效地提高模型的识别率。

2.2 实验结果对比

在完成训练后，使用不同条件下的测试集对模型进行评估，由于本文实验任务是对残缺的空/地X和空/地Y等2类信号进行分类，因此，在不同信噪比及不同残缺率下，各模型的召回率(Recall)、精确率(Precision)、F1-Score值对2种模型的预测结果进行评估。

2种模型的识别结果如表3～表5所示，可以看出，传统模板匹配算法在信噪比为-3 dB，残缺率为30%时，效果最差，精确率仅为66.4%。在信噪比为3 dB，残缺率为10%时，效果最好，精确率可以达到92.8%。而TC-CNN模型的精确率在信噪比为-3 dB，残缺率为30%时，精确率为84.4%；在信噪比为3 dB，残缺率为10%时，精确率可以达到99.8%。传统模板匹配算法的召回率、精确率及F1-Score的值在各残缺率下均低于TC-CNN模型，TC-CNN模型算法即使在较低信噪比的前提下(信噪比为-3 dB)，当信号的残缺率低于30%时，仍然可以达到84%以上的精确率。

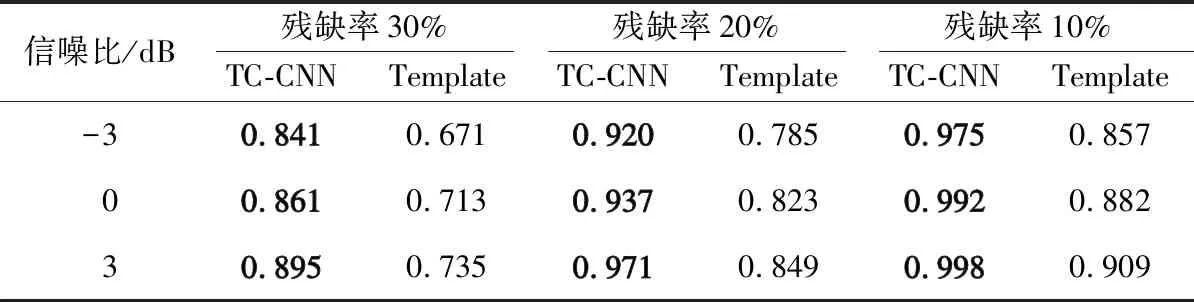
表3 各模型Recall评估对照结果

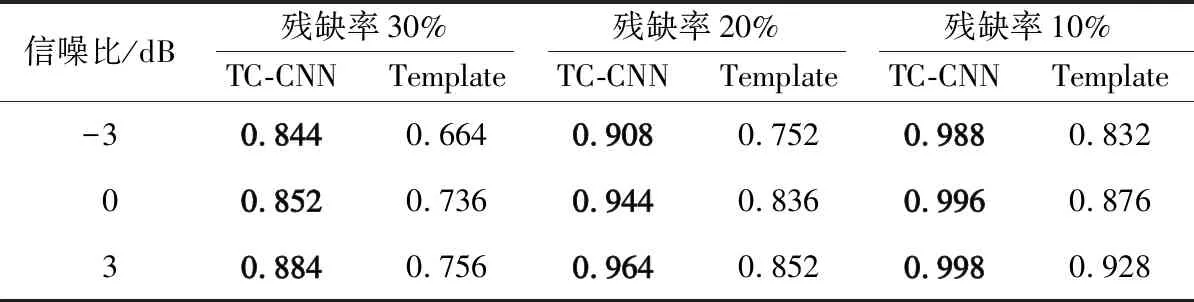
表4 各模型Precision评估对照结果

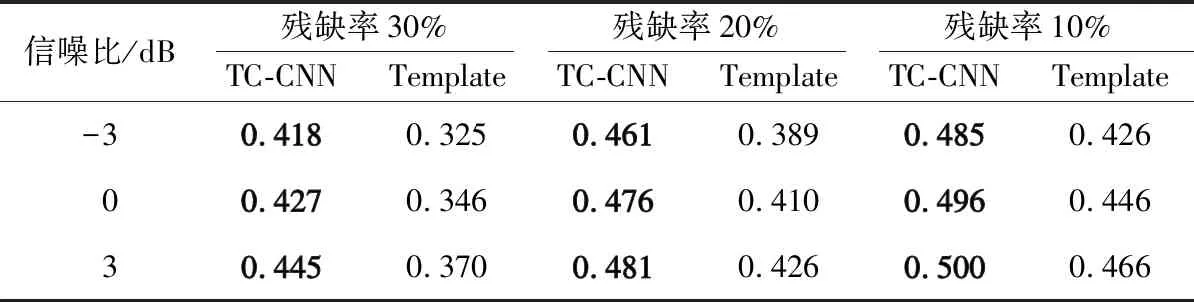
表5 各模型F1-Score评估对照结果

本文绘制了信噪比在0 dB且信号残缺率为30%时，传统模板匹配法和TC-CNN模型识别结果的混淆矩阵图，如图5和图6所示。

图5 信噪比为0 dB,残缺率为30%时模板匹配法识别结果的混淆矩阵Fig.5 Confusion matrix of the recognition result of template matching method when the signal-to-noise ratio is 0 dB and the defect rate is 30%

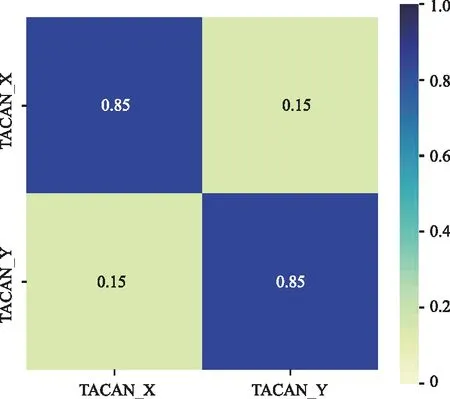
图6 信噪比为0 dB,残缺率为30%时TC-CNN识别结果的混淆矩阵Fig.6 Confusion matrix of TC-CNN recognition results when the signal-to-noise ratio is 0 dB and the defect rate is 30%

在该混淆矩阵中，纵轴代表实际的TACAN空/地信号类型，横轴代表预测的信号类型。由图5和图6可以看出，本文提出的TC-CNN模型方法在信号完整度较低的情况下具有更高的识别率。

3 结束语

本文通过研究信噪比和丢失率对TACAN空/地信号的影响，提出了一种基于改进的多层卷积神经网络模型TC-CNN。该模型对3种不同信噪比、不同信号残缺率下的TACAN空/地信号进行识别，并与传统模板匹配算法的结果进行了对比和评估。实验结果显示，传统模板匹配算法受信噪比和信号残缺率的影响较大，TC-CNN模型在保持较高识别率的前提下同时具有较好的鲁棒性。因此TC-CNN模型具有一定的实际应用价值。在后续工作中将继续考虑提升低信噪比的情况下，该模型的识别准确率。同时考虑加入不同的频率偏移以提高神经网络对实际信号中频偏的适应性。