重载齿轮齿条齿形设计与齿根应力计算方法研究

梁竞夫

（太原重型机械集团有限公司，太原 030024）

0 引言

随着我国经济的快速发展，矿山机械、工程机械和海洋工程装备等重型机械设备在能源、海洋、交通、冶金等领域被广泛应用，由于齿轮齿条传动具有结构简单、传动直接等特性，在这些设备中得到了充分应用。前几年这些大型设备的核心技术几乎被国外垄断，随着国内技术的不断发展，这些大型设备已经开始国产化，传动部件作为大型设备的核心部件，它的可靠性对于设备的性能起着至关重要的作用。

重载齿轮传动最致命的失效形式是断齿，断齿会给重型设备带来不可估量的损失，因此提高齿轮的弯曲强度是首要考虑的因素，对于重载齿轮齿条传动，通常都是采用大模数、小齿轮少齿数的传动方式，例如：对于自升式钻井平台的爬升齿轮，行业内基本取齿数为7，模数取80、100 mm等，根据平台承载能力大小确定；对于大型挖掘机的推压齿轮齿条传动，齿数通常取14，模数取40、50 mm等。

这些大模数的齿轮齿条传动设计目前没有设计标准可参考，也没有成熟的计算软件计算强度。目前设计还是通过有限元计算齿根应力，如果强度计算不通过，重新进行齿形设计，再建模，再进行有限元分析计算，设计过程很繁琐。本文研究齿形各参数对齿根应力及耐磨性的影响，导出齿形设计的计算公式，并针对齿形推导齿根应力的快捷计算方法。下列内容中的齿轮齿条指的都是重载大模数的齿轮齿条。

1 齿轮齿条的齿形设计

大模数齿轮齿条不适于采用通常的滚、插加工方法。对于小齿轮往往是根据齿形设计铣削加工工艺，对于齿条则根据齿形采取数控切割或铸造而成。为了便于制造，在矿用大型挖掘设备上推压齿轮齿形曾经采用过近似渐开线的3段圆弧组成，基圆以下是齿根圆弧，分度圆与齿根圆弧之间为一段圆弧，分段圆以上为另一段圆弧。在使用过程中传动误差大，引起振动，磨损严重。有的由于齿根圆弧设计不合理，出现过断齿现象。如何使齿形设计得到优化，解决问题的关键还是齿轮的各项参数指标。

1.1 齿顶厚

对于开式齿轮，齿顶太薄更容易磨损，建议齿轮顶厚S≥0.4m。上述适用于受疲劳载荷的齿轮齿条传动，对于钻井平台类承受静载荷的齿轮齿条传动，S≥0.15m即可。国外大型挖掘机推压机构XP2300、XP2800的推压小齿轮齿顶后分别为0.41m、0.42m，国外知名的NOV升降装置300 ft、400 ft自升式钻井平台的爬升小齿轮的齿顶厚分别为0.14m和0.15m。

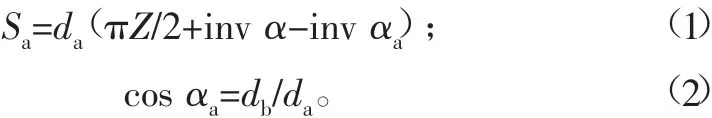
式中：da为齿顶圆直径；αa为齿顶压力角；m为模数。

1.2 重叠系数

对于受疲劳载荷的齿轮齿条传动，推荐重叠系数ε≥1.2，若重合度小，则啮合冲击大，对齿轮强度不利。对于钻井平台类主要承受静载荷的齿轮齿条传动，ε≥1.05即可。因为主要承受静载荷的齿轮齿条压力角通常都大于25°，重合度大，齿顶几乎变尖，容易产生塑变。

式中，ha2′为啮合点以上齿条有效齿顶高（如图1）。

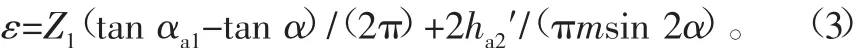
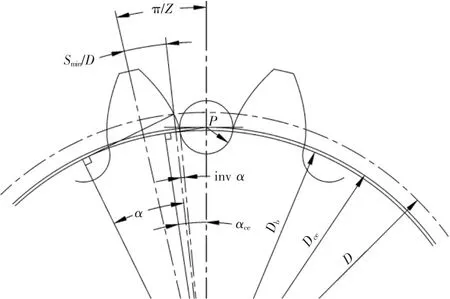
图1 重合度计算图形

根据使用工况，利用式（1）和式（2）可以求出齿顶圆直径da和齿顶压力角，同时满足式（3），有了齿顶圆直径，要看变位系数和齿轮的齿顶高系数的选取，若采用短齿大变位，齿轮齿厚加大，意味着啮合点齿条齿厚减小，齿轮强度加大，根据齿轮齿条等强度原则选择变位系数，齿轮正变位。

1.3 侧隙

考虑到开式齿轮齿条齿形制造误差、安装距的误差、周节累积误差、传动时齿面摩擦发热膨胀，齿侧间隙一般取0.12～0.15倍模数。齿侧间隙的留取通过减薄齿轮齿条的齿厚实现。齿条齿根厚度厚。

1.4 齿轮齿根圆角

在确定上述参数后，最终设计齿根圆角半径。

学生自主申报的科研项目，往往是由同一届学生甚至同班同学组成，重申请、轻完成的情况较为普遍[5]，项目申报时学生正处于积极性高、精力充沛的大二、大三阶段，学生在项目申报时表现积极，而在实施过程中因缺乏动力和持之以恒的精神，或者由于学生已临近毕业，导致项目尚未完成而中途放弃的现象。这种情况一方面影响下次的申报，另一方面也影响了带教教师的积极性。

齿轮齿根圆角采用单圆弧，相对齿轮而言，齿条危险截面的宽度比齿轮大，受载循环次数少，可以根据强度计算，齿根取双圆弧，齿条采用双圆弧可以减小齿根高，齿条基体增厚，齿条不易变形。根据需要选取齿条齿根圆弧半径，这里主要是针对齿轮齿根圆角研究。对于齿轮齿条的传动，在保证重叠系数和齿顶弧齿厚的情况下，齿轮最低啮合点基本在基圆上，通常比基圆大2～3 mm。齿根单圆弧与渐开线的切点设为该最低啮合点。齿根圆角半径rρ计算如下：

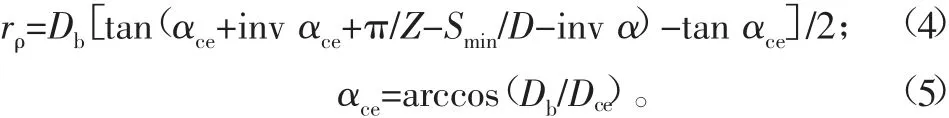
式中：rρ为齿根圆角半径，mm；Db为基圆直径，mm；αce为齿根圆弧与渐开线切点的压力角；Smin为分度圆实际齿厚，mm；α为分度圆压力角；Dce为齿根圆弧与渐开线切点的直径，Dce=Db＋（2～3 mm）。

1.5 齿条齿形

根据齿轮齿条的啮合特点，不管安装距是不是标准安装距，节点始终是在齿轮分度圆上。根据图2，齿条有效齿顶高ha2e计算如下：

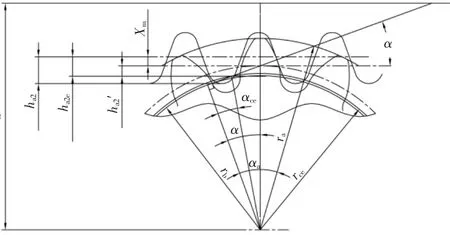
图2 齿条有效齿顶高计算图形

2 齿轮齿条齿根弯曲强度计算

对于重载大模数齿轮齿条传动的计算，有很多文献研究计算方法，有的用积分法，有的用映射函数法，在齿轮齿根弯曲应力的计算方法中，折截面比平截面计算的齿根应力更加精准，但折截面计算方法太复杂，用ISO的30°切线来确定危险截面的平截面法简单，而且试验表明两种方法计算的齿根应力相差不超过5%～6%。对于低速重载的大模数齿轮齿条，加工时都是采用特殊的刀具和加工方法，目前没有专门的计算软件。大部分是通过有限元分析法进行计算。有限元计算过程复杂，必须建模分析，不利于初始参数设计。研究一种针对大模数齿轮齿条强度的快捷解析计算方法便于设计计算。

这里特别注意的是，是按单齿啮合受力点还是按齿顶啮合受力点计算齿根应力。齿轮精度较高时，齿根应力按单齿啮合点进行计算；齿轮精度较低时，齿根应力具体是按哪一个方法计算，根据载荷分配系数Ka决定。

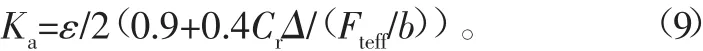
式中：Cr为同时啮合的两对轮齿迭加刚度系数的平均值；Δ为两齿轮的基节差；ε为重合度；Fteff为轮齿分度圆上的圆周力，Fteff=Ft·KA·Kv·KB；B为齿宽。

当Ka≤1时，说明齿轮单齿受力点受力最大；当Ka≥1时，说明齿轮传递的全部载荷作用于齿顶，齿根应力按齿顶受力进行计算。

低速重载的大模数齿轮齿条制造精度都难以保证，即使齿轮齿条啮合的重叠系数大于1.2，在齿传递载荷的过程中都是单齿受力，所以齿根应力应该按照齿顶受载进行计算，而不能按照单齿啮合点的受载计算齿根应力。参考文献[6]中，当齿轮精度低于11级时，齿根应力按照齿顶应力计算。

下面按照图3和图4推导专门用于低速重载的大模数齿轮齿条的齿根应力计算方法。

图3 齿轮图形

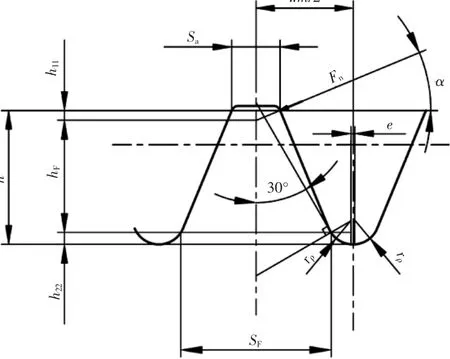
图4 齿条图形

根据ISO的30°切线来确定危险截面的平截面法（如图3），齿根应力计算公式为：

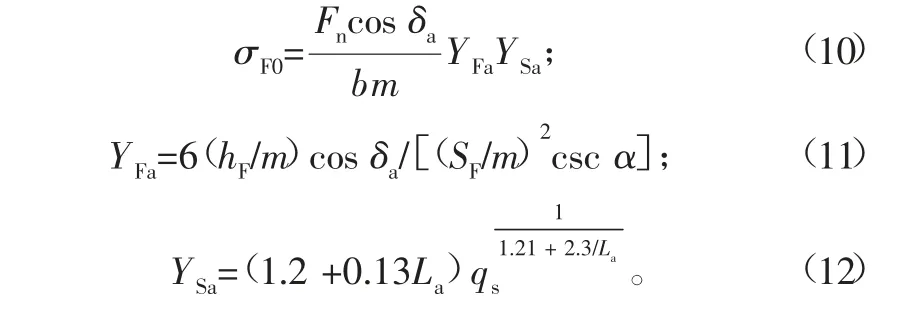
式中，危险截面的宽度SF和力臂hF是计算的关键参数，下面分别按齿轮和齿条推导这两个参数。

2.1 齿轮危险截面的宽度SF和力臂hF

按照齿轮图形（如图3），P点为齿根圆弧的圆心，SF=2AC，hF=L-OA，在△OPD中，∠POD=π/Z，根据图中三角形的几何关系，得出：

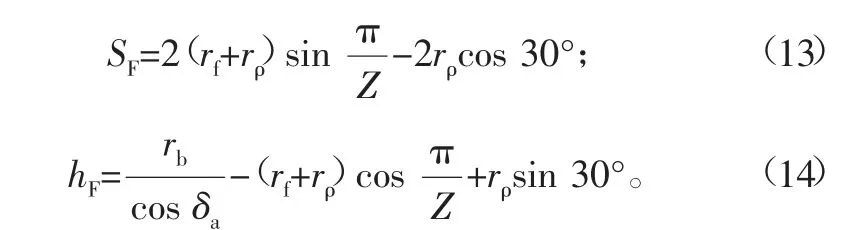
2.2 齿条危险截面的宽度SF和力臂hF

根据齿条图形（如图4），e为两齿根圆弧中心的距离，如果是单圆弧，e=0，齿条任意点的载荷角都等于压力角，推导的关系式为：

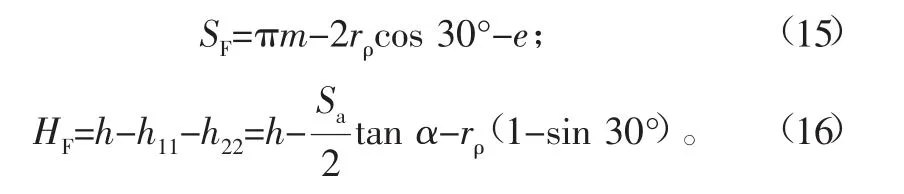
式中：h为有效齿条高度，mm；Sa为齿条有效高度的齿厚，mm；Fn为有效高度的齿顶法向载荷，N。

2.3 载荷角计算（如图5）

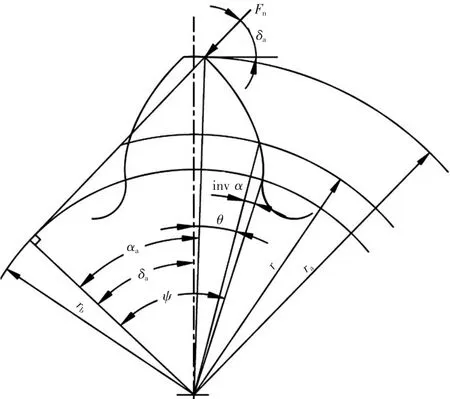
图5 载荷角计算图

3 实例计算验证

以300 ft自升式钻井平台升降装置爬升齿轮齿条传动为例，表1为小齿轮几何参数，齿轮齿宽为190 mm，齿条宽为177 mm，按照爬升齿轮的推压力2000 kN进行解析计算和有限元分析计算。

表1 小齿轮传动几何参数

3.1 齿形设计计算

根据式（4）和式（5），计算的齿轮参数如图6所示，齿根弧半径为35 mm，齿顶厚为0.15倍模数。

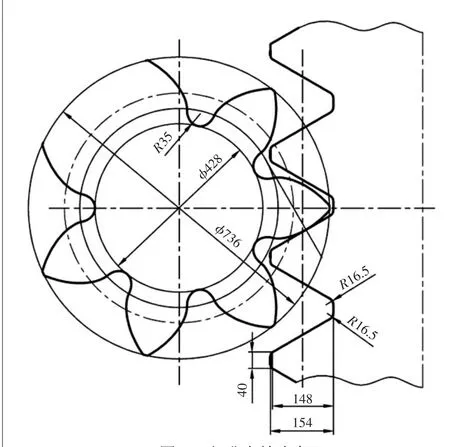
图6 爬升齿轮齿条

3.2 有限元分析计算

为了便于计算，取一对齿啮合进行计算（如图7），推压力加到齿条上，通过啮入与啮出两种状态计算齿条和齿轮的齿根应力。

图7 有限元分析计算

3.3 上述解析法和有限元分析法结果比较（如表2）

表2 解析法和有限元分析法的齿根应力结果对比

本文的齿根应力计算方法与有限元比较，最大误差约为5.1%，由于自升式钻井平台升降装置长期承受静载荷，齿根应力与齿轮、齿条各自材料的屈服强度比较即可。

4 结语

1）针对低速重载大模数齿轮齿条传动的失效形式，研究了特殊的齿形设计，以及齿形各个参数的匹配计算；2）通过载荷分配系数的计算，决定齿根应力是按全部载荷作用于齿顶还是按单齿啮合点进行计算；3）针对低速重载大模数齿轮齿条传动由于制造精度难以保证，载荷分配系数都大于1，根据ISO的30°切线来确定危险截面的平截面法推导出的齿根应力快捷计算公式，经过与有限元分析计算的值对比，误差不超过10%。