基于反余切函数的变步长LMS谐波检测算法*

张 展, 冷全超, 王 维, 杜诗扬

(河南理工大学 电气工程与自动化学院, 河南 焦作 454003)

0 引 言

随着电力电子技术的不断发展，电网中的谐波污染也日益严重，成为影响电能质量的主要问题，严重危害了供电的可靠性和电力系统运行的稳定性，必须进行有效治理[1]。有源电力滤波器(active power filter，APF)因其能快速地对频率和幅值都变化的谐波实现动态跟踪补偿，消除电网电流中的谐波成分，得到了广泛的应用。而APF的工作性能主要取决于对谐波电流实时准确的检测，因此寻找一种更快速、准确的电网谐波检测算法对治理电网的谐波污染是至关重要的[2]。目前，电力系统中最常见的谐波检测方法主要包括：瞬时无功功率检测[3]、快速傅里叶变换(fast Fourier transform，FFT)[4]、人工神经网络(artificial neural networks，ANN)[5]以及小波变换(wavelet transform，WT)[6]等。虽然这些方法都在谐波检测方面有着良好的表现，但是由于自身的缺陷限制了进一步的应用[7]。

自适应谐波检测算法，因其优秀的性能引起了国内外研究人员的关注[8]。但由于传统的自适应谐波检测算法无法解决收敛速度与稳态误差之间的矛盾，因此涌现出一大批优秀的改进算法。文献[9]中提出利用误差信号e(n)作为变量来参与进行步长更新，然而在实际系统中误差e(n)被噪声污染，这样就会引起较大的权值波动进而带来较大的失调误差;文献[10]提出利用归一化的处理方法改进权值公式，增大输入信号的动态范围，但其加大了算法的复杂程度，不易于工程应用的实现。为了能够解决上述问题，文献[11]提出了利用误差信号的自相关估计来调节步长更新；文献[12]提出VSSLMS-New算法，应用可变公式代替固定参数。虽然在步长更新时消除了不相关噪声序列的干扰具有较快的动态响应速度，但仍然没有很好地解决权值的收敛问题。

针对目前所面临的问题,本文提出了一种基于反余切函数的变步长谐波检测算法。首先针对权值收敛速度慢的问题，利用推导出来的三阶权值迭代公式来代替传统的权值迭代，以提高权值的收敛速度。其次针对稳态误差方面，提出使用反余切作为核心函数，并利用误差信号的自相关平均估计均值进行调节步长更新，以获得较小的稳态误差。并在仿真实验中进行了验证。

1 自适应谐波检测算法的工作原理

1.1 APF的自适应谐波检测算法

将自适应谐波电流检测算法应用于APF上的工作原理如图1所示。

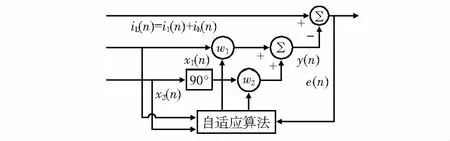
图1 自适应谐波检测原理

其中，iL(n)为非线性负载电流信号，i1(n)为非线性负载电流基波分量，ih(n)为高次谐波电流分量，参考输入信号x1(n)和x2(n)为电网同步锁相得到的标准正弦和余弦信号，y(n)为滤波器的输出期望信号，e(n)为用于调节权值系数的误差信号。其工作原理：将i1(n)作为噪声信号部分，ih(n)作为期望信号部分，以电网电压为基准信号，利用系统反馈误差信号e(n)进行控制权值的更新，使w逐渐增大逼近最优权向量w*，得到自适应滤波器期望信号y(n)，从而系统输出可变的畸变电流e(n)将逼近负载电流谐波分量ih(n)，经过iL(n)与y(n)差值得到负载电流谐波分量ih(n)。

记输入信号X(n)=[x1(n)x2(n)]T，权值系数W(n)=[w1(n)w2(n)]T，则自适应谐波电流检测算法可表示为

y(n)=WT(n)X(n)

(1)

e(n)=iL(n)-y(n)

(2)

W(n+1)=W(n)+2μe(n)X(n)

(3)

式中μ为固定的步长(0<μ<1/λmax),使算法能够快速收敛，λmax为输入信号自相关矩阵的最大特征值。

1.2 传统的变步长LMS算法

传统定步长LMS算法的自身局限决定其在收敛速度和稳态精度之间的矛盾是无法兼顾的,文献[12]提出的VSSLMS-New算法，应用反余切函数作为核心函数来调节步长更新，其步长更新公式为

η(n)=α·arccot(|e(n)|)

(4)

μ(n)=ζμ(n-1)+η(n-1)e2(n-1)

(5)

式中η(n)为反余切函数；μ(n)为动态步长因子；α为比例因子，用来调节反余切函数的取值范围；系数ζ决定收敛时的步长值。

VSSLMS-New应用可变公式代替固定参数，在一定程度上降低了计算的复杂度，提高了系统的跟踪性能；但由于该算法直接采用瞬时误差信号e(n)对步长进行更新，通常瞬时误差信号也含有大量的噪声，随着步长在更新的过程中极易受不相干噪声的干扰，并且其仍然采用最原始的权值迭代公式，权值收敛速度不够快，经常出现权值还未收敛，步长已达到最小值。

2 改进的变步长LMS算法

2.1 改进算法

通过引入e(n)e(n-1)获得误差信号的自相关估计均值，消除不相干噪声的干扰，进行控制步长的更新；并将其用在APF的谐波检测上，提出了一种新的LMS谐波检测算法,将其表示为LMS-NEW。其步长更新公式为

η(n)=∂arccot(|p(n)|)

(6)

μ(n)=δμ(n-1)+η(n-1)e2(n-1)

(7)

p(n)=mp(n-1)+k(1-m)e(n)e(n-1)

(8)

式(6)为反余切核心函数，其中，∂为比例因子；式(7)中，δ为调节收敛速度而设置的一个数值很小的正学习参数，可用来加快收敛速度；式(8)中，p(n)为误差信号的自相关时间均值估计反馈量，m为遗忘因子，用来调整历史信号影响程度，其值通常接近于1；k为影响因子，用来调节e(n)自相关对算法的影响，其值通常小于1。

2.2 改进算法的权值推导

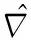
(9)

根据式(1)、式(2)和式(9)可以得到

(10)

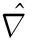
W(n+1)=W(n)+2μe(n)X(n)

(11)

式(11)即为LMS算法的滤波器权矢量迭代公式，μ为自适应滤波器的收敛系数。通过把当前时刻的权值系数矢量和误差函数作为比例因子进行相加得到自适应迭代下一时刻的权值系数矢量。因此，计算在n时刻的权值系数W′(n)[14]

W′(n)=W(n)+2μe(n)X(n)

(12)

e(n)=iL(n)-XT(n)W(n)

(13)

此时，W′(n)比W(n)更加接近最优权向量，梯度估值公式更新为

(14)

e1(n)=iL(n)XT(n)W′(n)

(15)

将式(12)、式(14)代入初始权值式(3)中，即可以得到式(16)；再结合式(12)、式(13)、式(15)、式(16)得到二阶权值式(17)，权值迭代公式如下

W(n+1)=W′(n)+2μe1(n)X(n)

(16)

W(n+1)=W′(n)+4μ(n)[1-μ(n)XT(n)X(n)]

e1(n)X(n)

(17)

利用此方法再进行权值公式的迭代，即可以得到新的权值迭代更新公式

W(n+1)=W(n)+φe(n)X(n)[6μ-12μ[μXT(n)X(n)]+

8μ[μXT(n)X(n)]2]

(18)

式中φ为比例因子干扰系数，通常为一个小于1的正值。理论上来说,迭代公式的迭代程度越高，获得到更快地权值收敛速度，但在实际仿真的过程中，权值的收敛速度具有一定的限度。在获得更高的收敛速度的同时也会带来更复杂的计算量，当权值迭代到一定次数后收敛速度就不会有明显的变化[15]。

2.3 改进算法的性能分析和比较

本文提出了一种新的LMS谐波检测算法表示为LMS-NEW。选择了与传统的定步长算法和文献[12]提出的LMS算法进行了比较。将传统的定步长算法以及文献[12]提出的算法分别表示为LMS-A,LMS-B。新算法采用可变的参数算法来替代步长更新中的固定参数，利用当前误差信号与上一时刻的误差信号的自相关平均估计均值做动态系数，可以消除不相关噪声的干扰；利用反余切函数自身的性质，即使在噪声信号产生干扰的同时，也能将步长控制在一个合理的范围。LMS-A采用固定步长需要进行大量的实验，才能获得合适的参数；LMS-B直接采用瞬时误差信号e(n)对步长进行更新，通常瞬时误差信号也含有大量的噪声，随着步长在更新的过程中也不可避免的被干扰，且仍采用最原始的权值迭代公式，严重影响了收敛速度。在此算法中，为了防止计算过程震荡，避免步长出现过大或者过小甚至是负值，需对变步长μ(n)限幅。即

(19)

式中μmin的选取一般满足算法的最低水平跟踪性能，通常为较小的正数；μmax的选取通常接近于算法收敛的临界稳定值。本文μmin取值为0.001，μmax取值为0.1。

此外，本文的改进变步长算法亦受δ,k和m等参数的影响；m为遗忘因子调节采样频率相关参数，用以控制过去的数据对现在状态的影响。m越大，表示过去的数据遗忘度越大，那么越早的数据对现在的影响也就越小；反之,m越小，历史数据遗忘度越小，则过去的数据对现在的影响越大。k为影响因子，加大误差信号对期望信号的干扰，在算法迭代过程中使得p(n)增大，使算法提高了对突变系统的跟踪性能，k的取值很小；通过尝试不同的电流值、不同系数下对算法进行多次仿真，发现单独的调节k和m的作用是等效的，δ参数对算法的收敛性与稳态性均有较大的影响；为了同时兼顾收敛速度和稳态误差性能，在之后的仿真实验中采取固定k和m，改变δ的值来调整检测算法的性能，最终获得参数的最优值。在实际运用的过程中，还需要根据谐波源的类型来调节控制参数，不同的谐波源对应着不同的参数，相同类型的谐波源负载可以通用同一参数。

3 变步长算法仿真分析

利用MATLAB/Simulink软件平台建立仿真模型，对LMS-A,LMS-B及改进的新算法LMS-NEW进行对比分析。将三相不可控整流桥接阻感负载作为谐波源，设置仿真电路电网相电压为220 V/50 Hz，R=20 Ω，L=20 mH，仿真时间为0.4 s，负载在0.2 s突变为R=10 Ω，L=20 mH。其参数为：LMS-A算法中μ=0.003 2；LMS-B算法中α=1.2×10-5,ξ=0.998；LMS-NEW算法中∂=2.4×10-6,δ=0.97,k=2×10-4,m=0.05；以A相电流为例，图2为负载电流波形。

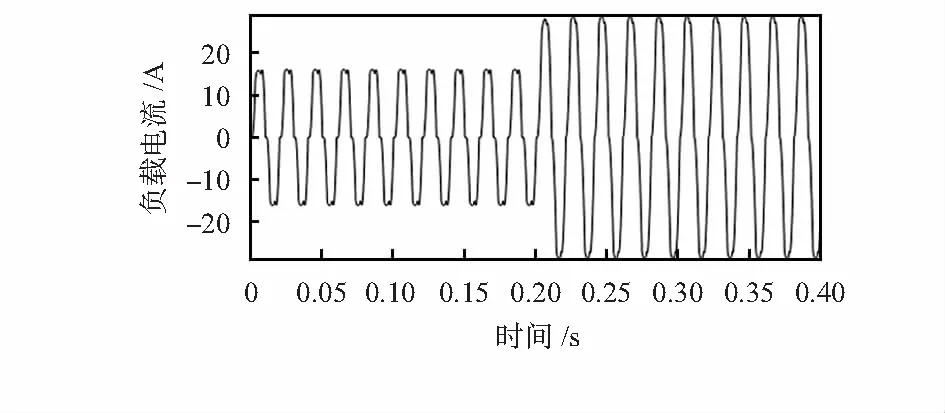
图2 负载电流波形

由图2可以看出,电流发生畸变，且负载电流中含有谐波和大量的噪声。之后,将负载电流进行FFT分析，可以得到负载电流的总谐波失真(total harmonic distortion，THD)。如图3所示负载在0～0.2 s的谐波含量THD=15.57 %，负载突变后0.2～0.4 s的谐波含量THD=9.55 %。

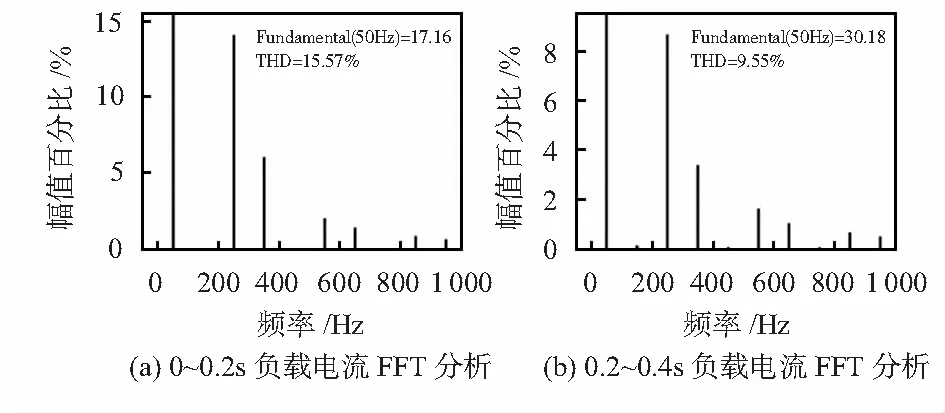
图3 负载电流的FFT分析

权值系数最能反映系统收敛的性能好坏，如图4所示。如图4(a)所示LMS-A谐波检测算法需要1个周期开始收敛；LMS-B谐波检测算法的收敛速度最慢，将近需要1.5个周期才能开始收敛；然而，新算法仅仅只需要0.5个周期就可以完成收敛。从图4(b)可以看出新算法不仅收敛速度快，而且收敛之后曲线波动最小，从而能说明稳态误差也是较小的。

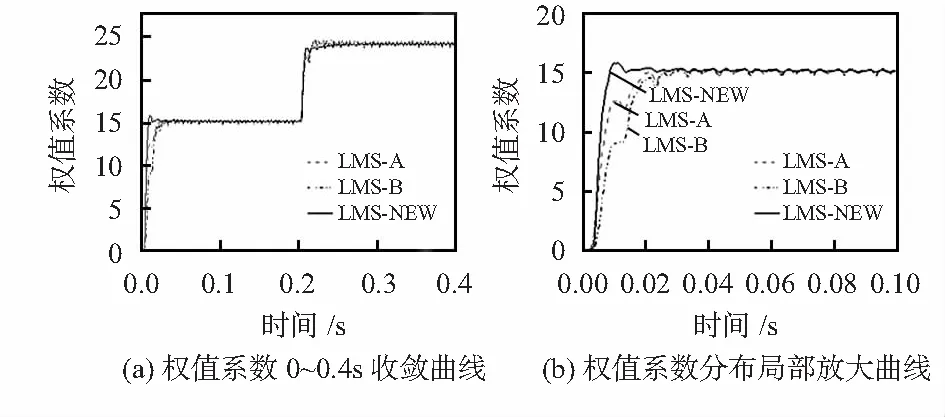
图4 权值系数收敛分布曲线

图5为3种算法检测到的基波电流波形对比，本文算法的跟踪速度远远大于其他2种算法的跟踪速度，跟踪精度最慢的是LMS-B算法。

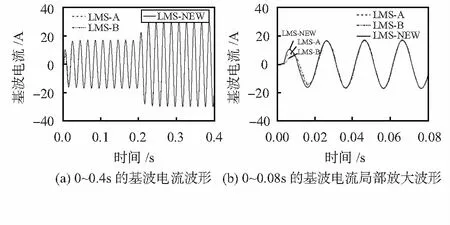
图5 3种算法的基波电流波形

为了进一步分析稳态误差，使负载在0.2 s时发生突变来验证新算法对时变系统的跟踪能力，负载电流在0.2 s后幅值突增，负载电流中的基波电流成分以及谐波电流成分也均发生突变。如图6所示，通过对LMS-A,LMS-B,LMS-NEW检测到的基波电流在0.3～0.4 s时间段内5个周期的波形进行FFT分析。其中LMS-A，THD=1.52 %；LMS-B，THD=1.11 %；LMS-NEW，THD=0.38 %。LMS-A谐波检测算法的收敛速度快于LMS-B，但其基波电流畸变率却是最大的。可以看出,LMS-NEW的THD远远小于其他算法，所以，LMS-NEW谐波检测算法检测出的基波电流更加接近工频正弦波。

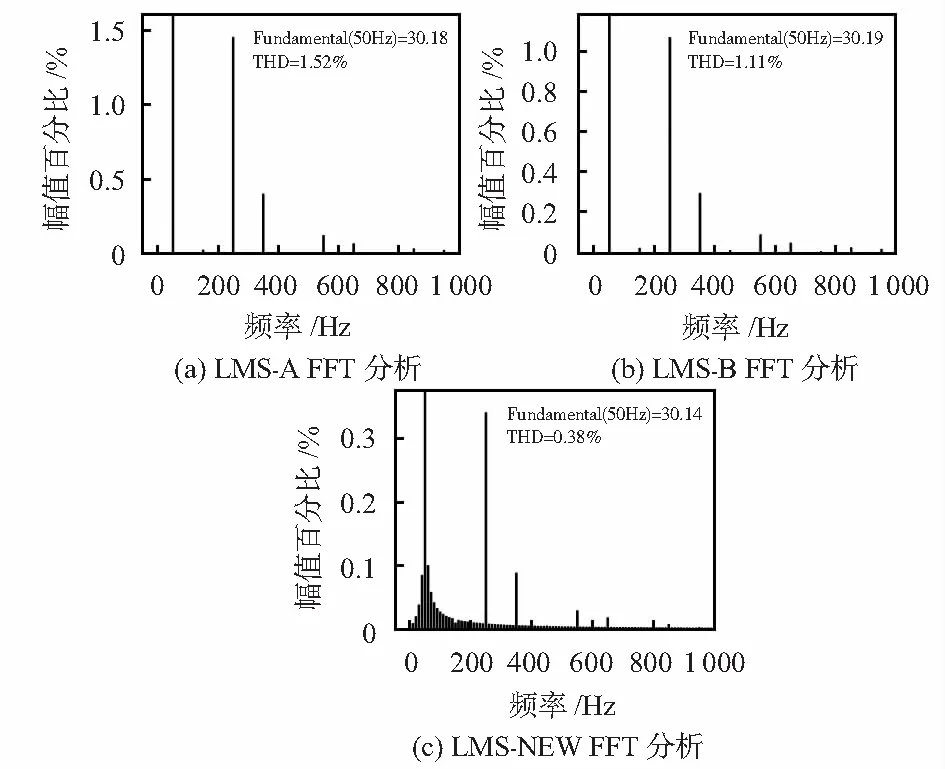
图6 3种算法基波电流的FFT分析

从以上仿真实验可以得出，在3种谐波检测算法中，LMS-NEW变步长算法检测出的基波有功电流的谐波畸变率低、稳态误差小、对系统负载发生突变时的跟踪能力强；并且在拥有较小稳态误差的同时，收敛速度也是较快的。

4 结 论

仿真结果表明:在进行谐波检测时本文算法能够有效地隔离噪声对步长影响，有着较好的跟踪性能，仅需要0.5个周期就可以完成跟踪到待检测的波形，基波电流的谐波畸变率相较于其他2种传统算法最低。且有着较小的计算量，在电力系统谐波检测方面比传统的检测方法更好地提高了收敛速度和减小了稳态误差。