基于UWB的加权自适应卡尔曼滤波室内定位算法*

郝占军， 安 莹， 陈红红， 党小超， 张金龙

(1.西北师范大学 计算机科学与工程学院，甘肃 兰州 730070； 2.甘肃省物联网工程研究中心，甘肃 兰州 730070)

0 引 言

传感网、物联网发展至今[1]，位置服务已然成为学术界所关注的焦点之一。相比于室外定位，室内环境中的多径效应与周边其他干扰因素使得室内精确定位面临更多的难题。国内外研究人员在室内定位中引入了一系列新兴的室内定位技术[2]：射频识别、WiFi[3]、超宽带(ultra-wide band，UWB)、蓝牙[4]、ZigBee[5]等。

UWB逐渐成为室内和结构化环境中高精度定位和跟踪的首选技术。文献[6]提出了一种基于UWB的贝叶斯滤波室内定位系统，采用线性回归模型校准距离测量误差，利用固定UWB基站与移动UWB基站的空间相关性来提高定位精度。文献[7]在实际煤矿环境下，结合惯性测量单元和UWB技术，通过卡尔曼滤波器融合后获得了较高的室内定位精度。由于传统的到达时间差(time difference of arrival，TDOA)定位技术通常需要精确的时间同步，部署难度较大。文献[8]通过引入LoRa技术来提高锚节点布局的灵活性，解决了TDOA锚节点之间时间同步的问题。卡尔曼滤波(Kalman filtering，KF)能够较好地适应于动态跟踪定位[9]。文献[10]运用EKF对UWB室内定位算法进行了改进，使复杂环境对测距的影响得到了有效地降低。

传统的KF在复杂室内环境下的误差抑制效果较差，所以本文采用误差补偿来减小测距过程中环境、行人等引入的噪声，并将KF中的过程噪声协方差和测量噪声协方差递归更新，利用递推估计进行加权自适应卡尔曼滤波(WKF)，实现了动态的跟踪定位。

1 WKF-TDOA算法设计

在UWB定位系统中，基站节点数目与定位精度成正相关。然而，出于对硬件成本等因素的考虑，基站的数量必须是有限的。本文采用四基站一标签的定位系统，针对KF定位中过程噪声协方差和测量噪声协方差的不确定性，提出了WKF-TDOA算法，算法流程如图1所示。

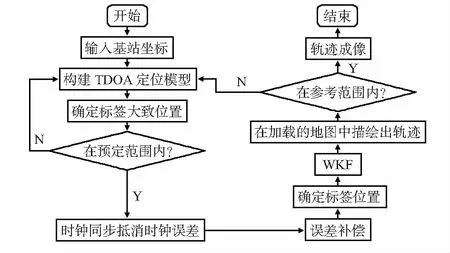
图1 WKF-TDOA算法流程

1.1 TDOA的获取

Step1 目标节点发送通知的时刻分别为R={R1，R2，R3，R4}，目标节点到各个基站的发送时延为τ={τ1,τ2,τ3,τ4}，而各个基站到目标节点的反馈时延为σ={σ1,σ2,σ3,σ4}，推出各个基站接收到信号的时刻T={T1,T2,T3,T4}

Ti=Ri-τi-σi,i∈{1,2,3,4}

(1)

Step2T0为待测标签同时向UWB基站发送信号的时刻，TOA可由各基站收到信号的时刻计算得出

ti=Ti-T0,i∈{1,2,3,4}

(2)

Step3 根据不同基站的TOA计算两个基站间的TDOA

Tij=ti-tj,i∈{1,2,3,4},j∈{1,2,3,4}

(3)

1.2 误差补偿

将小网格上的4个顶点作为参考点，用UWB节点测量4个参考点的位置坐标，在经过无线时钟同步后，记为Dw(Xi,k,Yi,k)，参考点的精确位置记为Dc，可计算出矢量修正值Dx

Dx=Dc-Dw

(4)

则4个参考节点的矢量修正值为Fi,i∈{1,2,3,4}，最后WKF-TDOA通过UWB节点测量目标节点的位置D，并使用修正值F对D进行修正，得到修正后的位置坐标DA

(5)

1.3 WKF

WKF-TDOA运用卡尔曼滤波器对过程和测量噪声协方差的不确定性具有自适应性这一属性，通过递归更新噪声协方差动态调整过程噪声协方差Qi,k和测量噪声协方差Ri,k的值。

系统的状态和测量方程为

xk=Fxk-1+wk-1

(6)

zk=Hxk+vk

(7)

式中xk和xk-1为时间为k和k-1时的系统状态，F和H为状态转移方程，zk为时间为k时的测量值，wk-1为过程噪声，vk为测量噪声，则其协方差分别为Qk和Rk。

滤波增益矩阵为

(8)

状态估计

(9)

预测的状态误差协方差矩阵为

(10)

其中,Q为过程协方差，假设Q中存在一个不确定的值称为ΔQ，则式(10)可写为

(11)

(12)

状态估计的测量值记为NQ，平均值和样本协方差分别为

(13)

(14)

结合式(11)和式(14)，通过数学计算可得

(15)

因为上述影响因子每次都会更新，故其上一时刻的协方差与目前位置的协方差就会具有一定的相关性，为获得其中的关联性，第一组的样本协方差可近似表示为

(16)

则式(15)可扩展为

(17)

其中

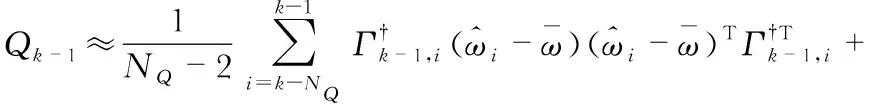
(18)

(19)

(20)

则

(21)

使用相同的近似值进行计算，结合式(8),式(9)得

(22)

在经过误差补偿与WKF之后，可以进一步提高定位精度，解算出最佳的标签位置。

2 实验测试与分析

2.1 实验环境

采用商用的I—UWB LPS定位系统，输出频率50 Hz，最大定位距离可达35 m，标签采用手持移动的方式，实验环境大小设置为3 m×3 m的室内空间，采用4个基站1个标签的定位模式，将4个基站以主从式基站组网，0#基站为主基站，其余3个基站为副基站，设备布设高度为1 m。实验分别设置在实验室、会议室及空旷的大厅分别进行测试，实验环境场景如图2所示。

图2 实验环境场景

2.2 不同状态比较

2.2.1 静态下的目标检测

在实验室、会议室及空旷大厅环境下，划分3 m×3 m的室内空旷区域，分别选取测试点C1、C2、C3进行测试，准确坐标为(0,2,1),收集测试点的位置信息，经误差补偿后各点在X，Y方向分量的偏差如图3～图5所示。横轴为采样个数，采样时间为10 s；纵轴为误差，单位为m。

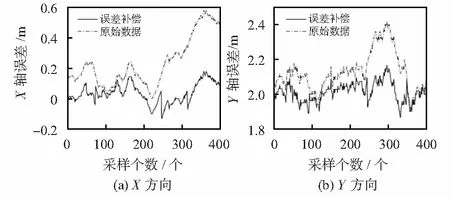
图3 C1点在X,Y轴上的偏差

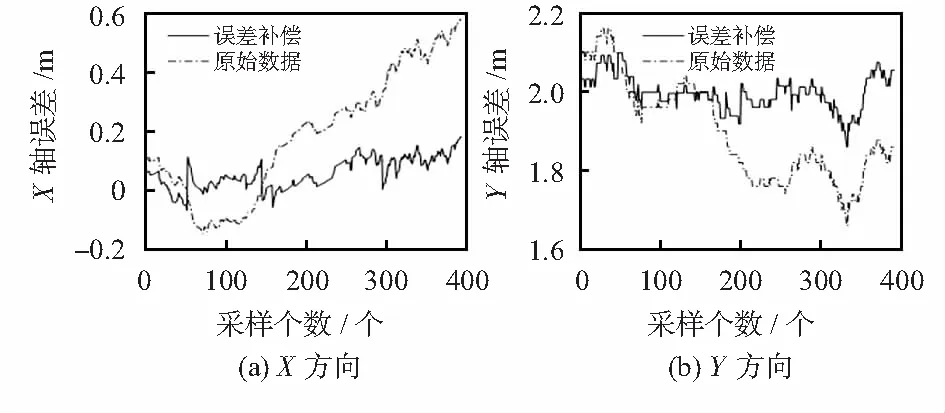
图4 C2点在X,Y轴上的偏差

图5 C3点在X,Y轴上的偏差

由静态目标实验可得，经误差补偿后三个点的静态测试结果在定位精度方面显著上升。对其最大误差(MPE)及均方根误差(RMSE)进行统计，见表1。

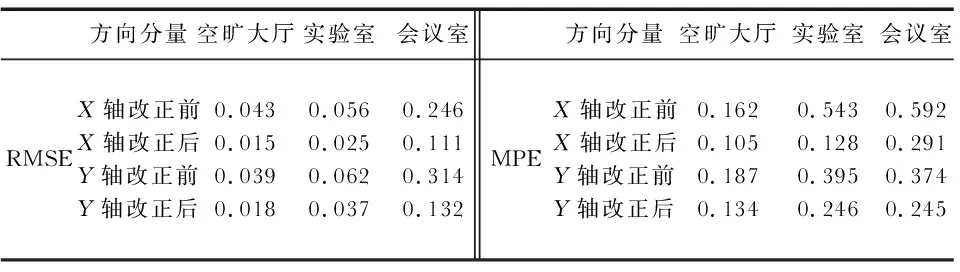
表1 均方根误差及最大误差 m

从表1可以看出，在经过误差补偿后，三种实验场景的均方根误差都有较为明显地减小，综合上述测试结果，可以看出，相较于前两个实验场景的定位结果，空旷大厅中存在的影响因素少，且在测试环境中无其他干扰信号的物体存在，定位精度显著上升，其测量曲线更平稳，与真实点位置信息相比存在差异较小，三个场景下的定位精度在经误差补偿后都有明显的提高，静态最大定位误差在0.3 m以内。WKF-TDOA能够较好地应用于经典的室内场景中，为不同室内环境提供更加精确便捷的静态位置服务。

2.2.2 动态下的目标检测

实验人员手持标签0分别在3个实验场景中行走，设置行走路径为矩形，同样选取3 m×3 m的室内空间，考虑到室内环境的不确定性较大，为保证测量结果的可靠性，携带标签的受试者均采取匀速运动。

图6(a)～(c)分别为在大厅、实验室、会议室环境下动态滤波之后的结果，可以看出,在动态多干扰因素的环境下，定位精度急剧下降，偏离真实轨迹，在卡尔曼滤波后，定位结果有所提升，但在误差波动较大的位置依然与真实轨迹有较大差别，经WKF-TDOA后，通过时域下动态调整权值，定位结果明显比传统KF后的结果更接近于预设轨迹，定位系统的鲁棒性得到了有效提升。

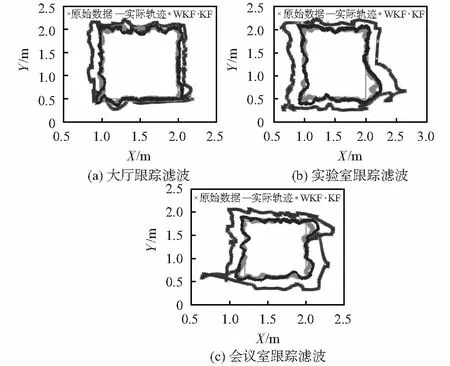
图6 空旷大厅运动轨迹

综上所述，在室内环境下，由于环境的多样性与环境内部的多径效应，单一的KF算法已经无法满足室内人员的精确位置服务，WKF-TDOA通过在时域内对测量路径进行WKF，使得滤波后的轨迹有效收敛于真实轨迹。实验证明，WKF-TDOA在复杂环境下对于人员的动态轨迹追踪有良好的应用，能为人员提供准确、有效的位置信息。

2.3 性能分析

2.3.1 不同基站数量比较

在实验室、会议室和空旷大厅三种室内环境下分别设置不同数量的基站进行单目标定位实验。不同基站数量对比下的定位结果如图7所示。

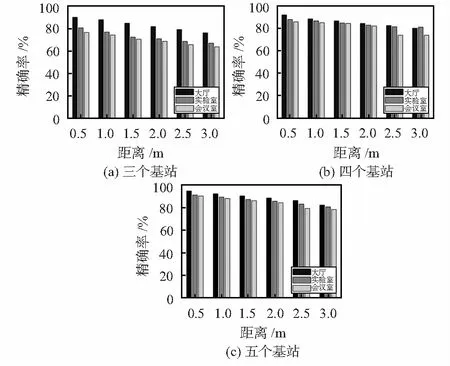
图7 不同基站数量对比

图7显示了同一个环境下不同基站数量对定位精度的影响，增大标签与基站的距离对三种不同环境下的定位精度都存在不同程度的影响，由图可知,在相对复杂的室内环境中，定位精度是随着基站数量而线性增长的，出于对实际应用环境考虑，在规模较小的室内复杂环境下部署四个基站足以提供稳定且准确的定位精度。

2.3.2 不同算法比较

对比方法有Taylor级数[11]、EKF以及最小二乘法[12]，采用RMSE、MPE作为评价指标。不同算法对比结果如图8所示。

图8 不同算法对比

图8可以看出，随着距离的增加，不同方法定位误差都有一定程度的上升，但EKF和WKF-TDOA定位误差相对较小，原因是两种算法不是单纯的定位算法，而是作为跟踪滤波算法，因此,在目标节点动态的情况下，EKF与WKF-TDOA的性能远优于Taylor级数法和最小二乘法。随着距离持续增加，经WKF-TDOA方法的识别误差更小，定位精度更高。

3 结束语

本文提出一种基于UWB的复杂室内定位算法—WKF-TDOA，综合静态与动态两种标签移动状态，使用误差补偿对采集的UWB数据进行修正。动态的情况下，本文将噪声协方差进行递归更新，动态调整权值以增强滤波器的稳定性，改进了传统的KF方法，进一步提高了定位精度。实验在多个真实的室内环境中进行，结果表明：WKF-TDOA在复杂室内环境下定位精度有很大提升，在静态与动态的环境中定位精度较高，具有较强的普适性，可在多种室内场景下进行使用。在后续工作中，将研究在室内复杂环境下多人精确定位的问题，进一步提高算法的普适性与鲁棒性。