基于改进VSM的城轨牵引系统自适应协同控制
杨成顺,刘国富,戴宇辰,张东东,黄宵宁
(1.南京工程学院电力工程学院,江苏 南京 211167;2.武汉理工大学自动化学院,湖北 武汉 430070)
近年来,城市轨道交通作为我国现代化城市的便捷交通工具,因其节能、快速及运量大等优点,逐渐地被广泛应用,有效地缓解了我国交通拥挤的状况[1-2]。城市轨道交通主要由电网系统、通信系统、控制系统、城轨列车、接触线路、牵引供电系统等组成,其中最为重要的就是牵引供电系统,在牵引供电系统控制良好的情况下,才能够为城市轨道交通的运营提供安全、优质、可靠、稳定的电能[3-5]。因此,如何改进牵引供电系统的控制性能逐渐成为目前研究热点问题。
目前,一些传统的控制方法包括直接电流、dq解耦控制和下垂控制等已经应用于牵引供电系统中,但是由于系统的非线性特征,传统的控制方法在保证系统的动态性能和控制效果等方面有着明显的不足。例如,文献[6]提出了一种改进的下垂控制方法,并通过电压偏移和负载电流前馈控制等方法,消除了下垂控制引起的电压偏差,提高牵引接触网电压控制的动态性。这些方法虽然能够在城轨列车运行时控制直流母线电压,实现正常的牵引供电状态,但是仅仅将城轨列车看作是被动的负载。在发生暂态扰动时系统会发生直流母线电压的波动以及频率的波动,此时,列车不具备主动参与调节牵引网直流母线电压和频率调节的能力,从而会造成牵引系统的不稳定。虚拟同步机(virtual synchronous machine,VSM)通过模拟传统同步机主动调频和无功调压的外特性,为系统增加惯性和阻尼,进而改善系统暂态性能,特别是其虚拟参数不受物理约束,从而惯性和阻尼参数可以实时调节。因此,研究改进VSM技术控制的牵引供电系统,能够使城轨列车具有同步机的主动调频和无功调压的外特性,使城轨列车由传统的被动负载转变为能够主动参与牵引网调节的特殊负载,在系统发生暂态扰动时,能够减缓牵引网直流母线电压和频率的波动,逐渐地恢复稳定。
近年来,虽然已经有很多学者在VSM方面做了很多的研究和应用,但是大部分学者仅仅研究将VSM技术应用于逆变器的控制。文献[7]在微网方面提出了一种改进bang-bang控制的VSM自适应虚拟惯量控制策略,能够减少频率超调并加快了响应速度;文献[8]在光储方面建立了光储VSM模型并采用自适应控制的方法,优化了系统的动态性能;文献[9]在背靠背启动方面采用了VSM技术,优化了启动系统并且提高了控制的精准度。从这些文献中可以看出VSM应用于多个方面并且都产生了较好的效果,然而,上述所有参考文献都提到将VSM应用于逆变器的控制,而VSM应用于整流器控制的相对较少。文献[10]基于阻抗分析法,比较研究了VSM控制的整流器和传统整流器在弱电网下的稳定性,验证了VSM可减少系统波动、增强系统稳定性的优良特性。同样地,如果将VSM应用于城轨列车的整流牵引过程中,则将会减少系统的波动,增强系统的稳定性,从而提高牵引网应对暂态扰动的能力。因此,研究VSM应用于牵引供电系统将具有重要意义。此外,在城市轨道交通中通常包含多个牵引变电站(traction substations,TSSs),应需考虑多个TSSs在牵引供电系统中协同运行的过程,即需要考虑多个VSM系统的协同运行。文献[11-12]采用了惯性中心的控制方法,使每个VSM系统在发生扰动时频率能够尽快地趋于一致,从而快速恢复稳定。但是,此方法是集中式的,不适用于城轨牵引供电系统。
基于以上分析,本文提出了一种基于改进的VSM的自适应协同控制(adaptive cooperative control based improved VSM,IVACC)的方法。首先,在传统的VSM的基础上,提出了一种适应于牵引整流器的改进VSM(improved VSM,IVSM)方法来作为牵引供电系统的一次控制策略,使系统频率和直流母线电压自动调节以恢复稳定;其次,在一次控制的基础上,采用基于一致性的自适应协同控制作为二次控制策略,以此来自适应调节虚拟参数,从而优化牵引供电系统的动态响应性能;然后,考虑到多个TSSs之间的相对距离以及参数的不同,采用了多智能体协同控制技术,使TSSs在列车运行时能够根据实际情况进行自适应调节,从而维持牵引网系统的稳定;最后,使用Matlab/Simulink仿真验证了所提出控制方法的有效性。
1 城市轨道交通系统架构
城市轨道交通的系统基本结构如图1所示,主要由交流电网、多个TSSs、直流牵引网、城轨列车、可再生能源系统以及电能设备组成。详细组成部分如下[13-15]:
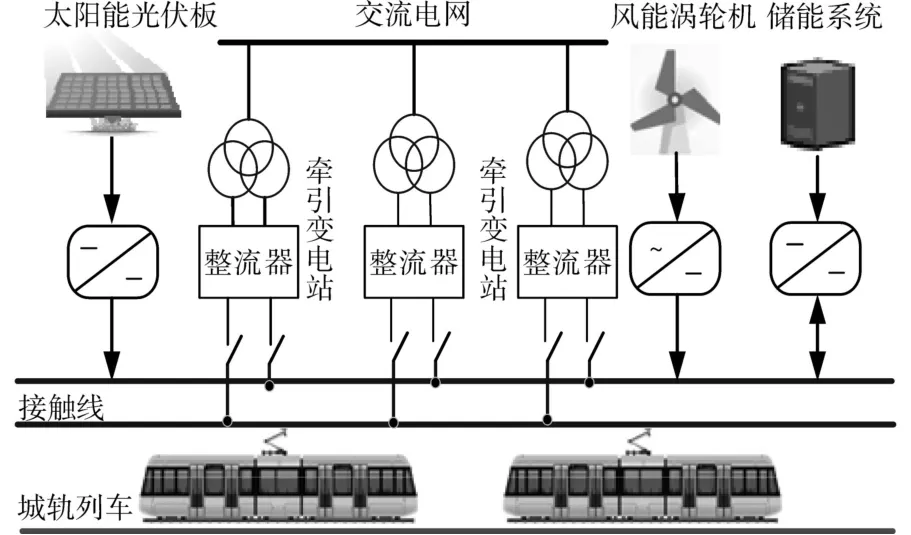
图1 城市轨道亚通系统结构图Fig.1 Structure diagram of urban rail transit system
1)TSSs,每个装有改进VSM的输电系统通过降压变压器连接到高压三相公用电网,并将交流电转换为直流电用于电力牵引。
2)直流牵引网,单个直流牵引网接触线不间断地铺设在较大的区域范围内,通过电力电子转换器连接着所有单元。
3)可再生能源,如光伏和风能等,可以通过直流-直流或交流-直流转换器连接到单个直流牵引网,作为牵引系统的辅助电源。
4)电能设备,如电池、超级电容器和飞轮在内的储能系统等,可以通过双向换流器连接到直流牵引网接触线上,以补偿能量或回收再生制动产生的能量。
从系统结构可以看出,城市轨道交通的能量在三相电网、可再生能源和一些电能设备中相互交换。在城轨列车正常运行中,列车消耗的能量可以由TSSs和可再生能源来提供。在某些情况下,城轨列车也可以将再生制动产生的能量回馈到电能设备,以便补偿运行中消耗的能量。此外,在再生制动能量不能被线路上的列车完全消耗的情况下,可以将能量用于备用或者提供给其他辅助用电设备,防止直流母线电压因制动能量较多而急速升高。在更糟糕的情况下,如果交流系统故障持续一段时间,可再生能源和电能设备可以控制系统的输出电源需求。由于系统的复杂性,文中只考虑多个TSSs之间的协调控制,不再考虑可再生能源及一些电能设备。
2 适用于牵引系统的虚拟同步机策略
2.1 传统的VSM原理
虚拟同步机技术的核心是采用同步机的转子运动方程和定子电气方程(或涉及定转子间电磁关系式),完成机械部分和电磁部分建模,以模拟转动惯量与电磁暂态特征,并检测电网频率和电压变化,依据一次调频和励磁控制算法从外特性上模拟有功调频和无功调压过程。从现有的研究来看,传统的VSM的转子运动方程比较一致,以第i个系统为例,则其转子运动方程为

式中:Ji为虚拟惯量,表示系统的惯性程度;Di为反映阻尼程度的虚拟阻尼系数,可使VSM具有阻尼震荡的能力,同时也可表征有功-频率的一次下垂特性;θi.r为VSM的功角;ωi.r为VSM的角频率;ωn为额定角频率;Ti.m,Ti.e分别为VSM的模拟机械转矩和电磁转矩。
Ti.m和Ti.e可表示如下:

式中:Pi.m,Pi.e分别为系统的机械功率和电磁功率。
传统的VSM电气方程一般采用电压下垂控制的励磁调节,则无功功率和电压之间满足下垂特性,则有:

式中:Ui.n为交流侧额定参考电压;Ui.r为参考电压幅值;qi为下垂控制系数;Qi.m为无功功率参考值;Qi.n为系统的实际无功功率。
2.2 适用于牵引系统的改进的VSM原理
传统VSM工作模式一般应用于逆变器的控制,即电流从换流器侧流向牵引网侧;而考虑到城轨列车运行时,牵引系统主要工作于牵引工况,此时电流方向是从牵引网流向TSS,即换流器侧,这正好与传统虚拟同步机的工作模式相反。假设定义电流正方向为牵引网流向换流器侧,则在传统的VSM的基础上需要进行调整,具体为功率符号相反,进而虚拟电磁转矩以及虚拟机械转矩符号也会相反,从而得到适用于牵引系统的转子运动方程为

另外,对于城轨列车的牵引系统而言,其最主要的目标是要保证直流牵引网的电压为额定参考值,故保持定子电气方程不变,在式(4)的基础上,将功率外环改进为电压外环,则改进的虚拟同步机的转子运动方程再次改进为

式中:ui.dc为直流牵引网电压;ui.m为牵引网参考电压;ki.p,ki.i为PI的参数。
图2为适用于牵引系统的改进的虚拟同步机的拓扑结构图,可以看出,电压外环由转子运动方程产生转子角,可以使得城轨列车在发生扰动时具有类似同步机的外特性,具有一定的惯性和阻尼的支撑。在无功功率回路中,采用传统的下垂控制产生参考电压幅值,然后由转子角和参考电压幅值形成三相参考电压,其中虚拟惯性和虚拟阻尼在VSM整流器中起着不同的作用。简而言之,虚拟惯性决定了频率变化的响应速度;虚拟阻尼可以抑制并网模式下的频率振荡,并决定各VSM的功率分配。值得注意的是,VSM的惯性和阻尼可以根据不同的要求灵活调整。接下来将主要研究虚拟惯性和虚拟阻尼对VSM动态性能的影响,从而优化城轨列车的牵引系统。

图2 改进的VSM拓扑结构Fig.2 The topology of improved VSM
3 基于一致性的自适应协同控制
3.1 改进虚拟同步机技术参数分析
虚拟惯量决定了转子保持当前运动状态的能力,模拟了同步机转子所具有的机械惯性;对于虚拟阻尼,控制策略可以在电压变化过程中描述对应的电流变化量,从而反映了虚拟同步机阻尼振荡的能力。

首先,针对虚拟惯性来说,由式(5)可得:同步机的转动惯量取决于转子的物理特性,为恒定常数;而VSM的虚拟转动惯量为虚拟量,在一定时,虚拟惯量与角频率变化率成反比,虚拟惯量与频率变化有关,可以自适应调节,从机理上证实了VSM虚拟惯量进行自适应变化的可行性。
虚拟惯量和频率之间的关系如图3所示,可以看出,在第4 s时系统发生扰动后,虚拟惯量越大,频率的响应时间越长,超调量越大,但是频率的变化率越小,从而在仿真中证实了虚拟惯量与角频率变化率的关系。
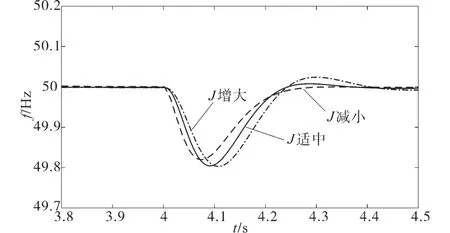
图3 虚拟惯量与频率之间的动态响应曲线Fig.3 Dynamic response curves between virtual inertia and frequency
其次,针对虚拟阻尼来说,同理由式(5)可得:
虚拟阻尼和频率之间的关系如图4所示,可以看出,在第4 s时系统发生扰动后,阻尼越大,频率的超调量越小,响应速度越快,偏差越小,从而在仿真中证实了虚拟阻尼与频率偏差的之间的关系。
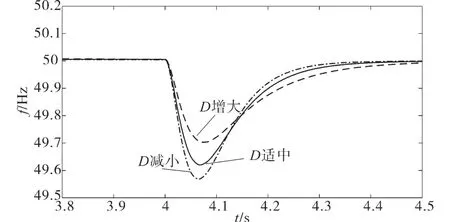
图4 虚拟阻尼与频率之间的动态响应曲线Fig.4 Dynamic response curves between virtual damping and frequency
然后,根据虚拟参数与频率之间的关系分析可知,VSM的虚拟惯性和虚拟阻尼会同时影响频率的动态响应,从而影响整个系统。因此,在系统发生扰动时,需要同时调节虚拟惯性和虚拟阻尼,以便使系统尽快地恢复稳定。
3.2 改进虚拟同步机技术参数设计
根据对改进VSM技术的参数分析可以得到,就虚拟惯性而言,系统大惯量可以减少暂态过程中的频率偏差变化率,但是增加频率的超调量,从而导致系统偏差较大,响应速度变慢;系统小惯量具有很快的响应速度,然而在大扰动和系统突变的情况下,小惯性系统却容易导致电压和频率出现严重偏差,从而影响系统稳定性和可靠性。同样,就虚拟阻尼而言,系统大阻尼可以减少暂态过程中的频率偏差,减小超调量,加快响应速度,但是阻尼过大会导致系统不稳定;系统小阻尼可以使系统处于稳定状态,但是会增大超调量,增大频率偏差,响应速度会变慢。因此,综合考虑虚拟惯量和虚拟阻尼的特性来设计改进虚拟同步机技术参数。
图5为单个系统发生扰动后,因角频率偏离电网额定角频率值,故需要在相应的阶段调整虚拟参数,使系统尽可能地快速恢复稳定。在t1—t2期间,频率逐渐偏离电网额定角频率,并始终大于电网角频率,而且角速度的变化率先急速增大后逐渐变小,因此,为抑制频率的偏移程度,此过程中应增加虚拟惯量来抑制角频率的变化率,并增加虚拟阻尼抑制角频率的偏差;在t2—t3期间,频率逐渐返回电网额定角频率值,并也始终大于电网角频率,而且角速度的变化率反方向从零逐渐增大,因此,为抑制频率的偏移程度,此过程中应减小虚拟惯量来抑制角频率的变化率,并增加虚拟阻尼抑制频率的偏差。在t3—t4和t4—t5期间可类比t1—t2和t2—t3期间,根据频率的变化实时调整虚拟参数,如表1所示。
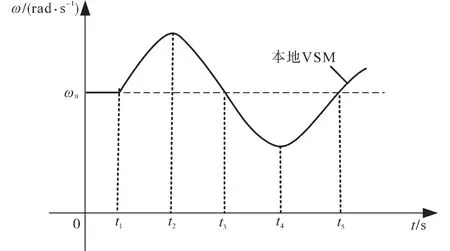
图5 本地VSM系统受干扰时的频率振荡过程Fig.5 Frequency oscillation process of local VSM system during disturbance
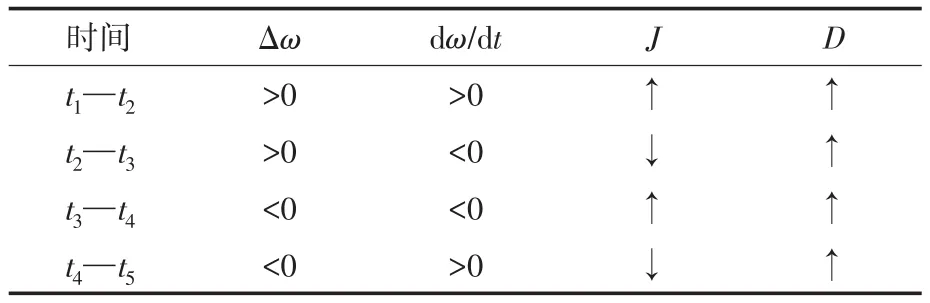
表1 本地VSM的虚拟惯量J和虚拟阻尼D的设计Tab.1 Design of virtual inertia J and virtual damping D for local VSM system
此外,除了要考虑在本地TSS中VSM系统的参数设计,还应考虑多个TSSs中VSM协同的参数分析和设计,使在系统发生扰动时,多个TSSs能够保持响应的一致性,在一定时间内尽快地恢复稳定。
3.3 自协同参数分析与设计
鉴于多个TSSs之间的供电距离以及参数设置的不同,利用局部变电站感知相邻变电站之间的信息的作用进行协同控制,考虑将每个变电站VSM系统看作一个代理机构,每个代理看作一个智能体,利用多智能体协同控制技术使多TSSs中VSM系统进行自协同控制。
图6为多个TSSs中VSM系统发生扰动后的本地VSM和协同VSM系统受干扰的频率振荡过程。因各TSSs的参数不同以及相对距离的影响,在系统受到干扰时,每个TSS的频率变化也不相同,故而需要进一步调整每个变电站VSM系统的虚拟参数,以达到频率响应的一致性,使系统快速地恢复稳定。以本地VSM为例,在t1—t2期间,频率逐渐偏离电网额定角频率,并且本地VSM系统的频率偏移量大于协同VSM,频率变化率小于协同VSM,因此,为使得系统能够尽快稳定,则需要使本地VSM系统根据协同的VSM进行实时调节虚拟参数,故而此过程中应增加虚拟惯量并增加虚拟阻尼。在t2—t3期间,本地VSM系统的频率偏移量大于协同VSM,但是频率变化率小于协同VSM,此时本地VSM应减少虚拟惯量并增加虚拟阻尼。在t3—t4和t5—t6期间可类比t1—t2期间,在t4—t5期间可类比t2—t3期间,根据协同VSM的频率变化实时调整本地的虚拟参数,如表2所示。

图6 本地VSM和协同VSM系统受干扰的频率振荡过程Fig.6 Frequency oscillation processes of local VSM and cooperative VSM systems
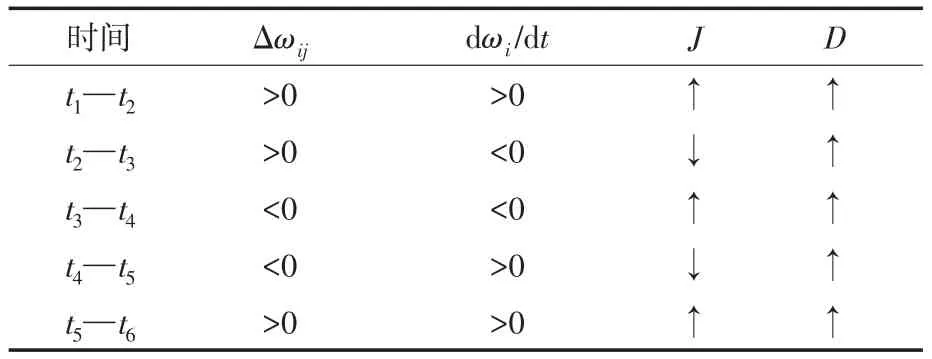
表2 协同VSM的虚拟惯量J和虚拟阻尼D的设计Tab.2 Design of virtual inertia J and virtual damping D for collaborative VSM system
3.4 基于一致性的自适应协同控制
根据以上的参数的分析和设计,提出了一种基于一致性的自适应协同控制方法以改进虚拟参数来作为二次控制,优化系统的动态响应性能。由表1和表2的设计原理可以得到:
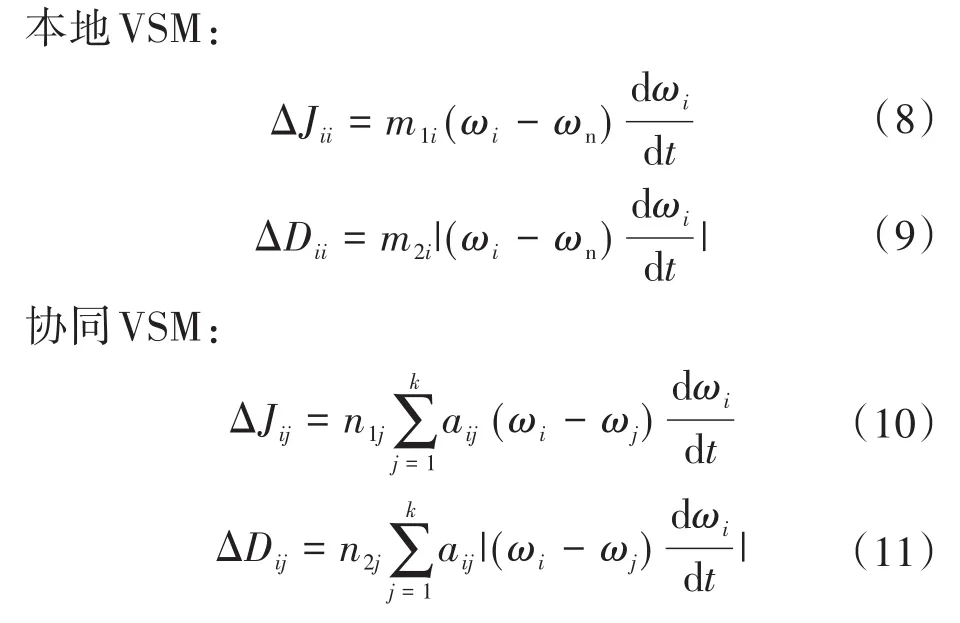
式中:ωi,ωj分别为本地VSM系统和协同VSM系统的角频率;dωi/dt为本地VSM系统的角频率变化率;ΔJii,ΔDii分别为本地系统模糊控制的自调整转动惯量、自调整虚拟阻尼;ΔJij,ΔDij分别为本地系统根据相邻系统模糊控制的自协同调整转动惯量、自协同调整虚拟阻尼;m1i,m2i,n1j,n2j为正调节系数,与调节本地VSM系统频率动态响应速度有关;aij为多智能体通讯信息。
aij表示为

综上,根据以上介绍和分析,最终得到了基于共识的协同自适应控制的方法,其基本公式如下:

式中:Ji.0,Di.0分别为本地系统的初始转动惯量和初始虚拟阻尼;Ji,Di分别为本地系统的总转动惯量和总虚拟阻尼。
此外,为了使每个系统能够稳定地运行,需要设计虚拟参数的边界,以满足正定性和有界性,定义:

式中:Ji.max,Ji.min,Di.max,Di.min分别为虚拟参数的自适应上界和下界。
4 仿真结果和分析
为验证所提控制策略的有效性,基于图7,本文采用Matlab/Simulink模拟城轨交通牵引系统的模型进行仿真分析。本文考虑三个TSSs和一列列车,假设其中TSSs之间的相对距离为4 km,列车此时距离TSS 1#为1 km,距离TSS 2#为3 km。此外,本文将采用城轨列车运行过程中的两个案例情况来进行仿真分析和验证,一方面考虑列车移动过程中,列车功率的提供是由列车与TSSs之间的相对距离来决定的;另一方面,以列车运行中牵引负荷的变化来验证所提控制方法的性能。表3给出了牵引系统的部分参数,表4给出了所提控制策略的相应参数,其中虚拟参数的初始值设置都是不同的。
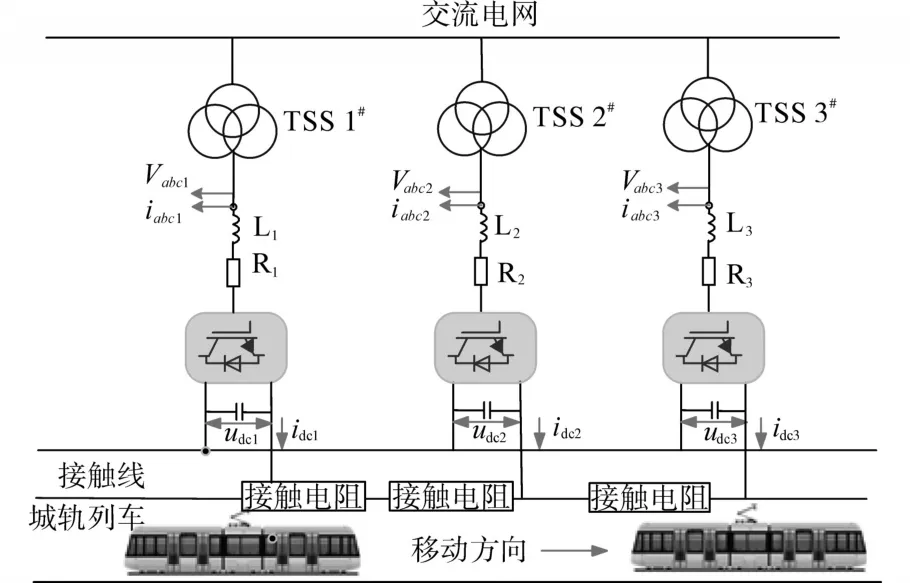
图7 城市轨道亚通牵引系统拓扑结构图Fig.7 Topological structure diagram of urban rail transit traction system

表3 牵引系统的部分参数Tab.3 The partial parameters of the traction system

表4 改进的VSM系统参数Tab.4 The parameters of improved VSM system
4.1 案例1:移动列车下控制方法的测试
此案例主要研究了连接在接触网和移动列车上的三个TSSs,在列车移动过程中,列车与每个TSS的相对距离中接触电阻的变化和参数设置的不同,从而会导致TSSs功率分配的不同。在仿真中,假设列车在t=5 s时从其初始状态开始每5 s向右移动2 km,仿真结果如图8所示。
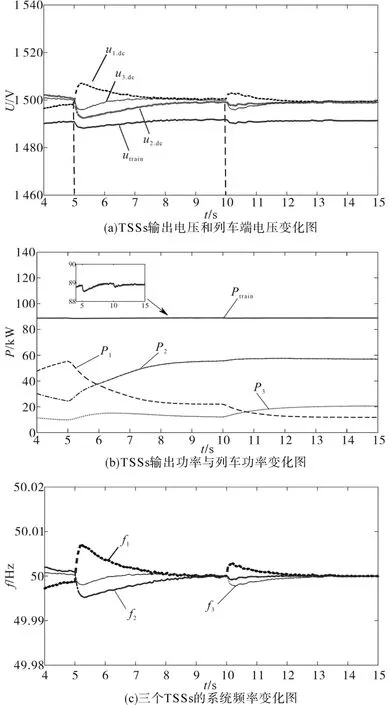
图8 移动列车下仿真结果图Fig.8 Simulation results under mobile train
在t=5~10 s期间,列车移动了2 km,由图8a可以看出,列车运行时,除短时暂态过程外,列车端电压稳定,而且可以看出TSS 1#电压变化幅度最大,TSS 3#变化最小,这是因为列车初始状态距离TSS 1#最近,距离TSS 3#最远。并且,列车的功率大部分是由TSS 1#和TSS 2#来提供的,如图8b所示。在此期间,三个TSSs系统的频率变化情况与电压变化相同,由于惯性和阻尼,三个TSSs系统的频率逐渐稳定,如图8c所示。
在t=10~15 s期间,列车又右移动了2 km,因列车逐渐地靠近 TSS 2#和 TSS 3#,远离 TSS 1#,故而TSS 2#和TSS 3#供给列车的功率开始逐渐地增多,如图8b所示,因此,功率分配由列车和TSSs之间的相对距离来决定。同样地,在t=10~15 s期间,如图8c所示,列车的端电压经过短期瞬态过程后恢复稳定,频率也逐渐稳定,TSS 1#电压和频率变化的幅度也变小,从而验证了列车的实际运行。
4.2 案例2:牵引负荷变化下控制方法的动态性能
为验证所提出的IVACC方法的性能,此案例主要研究了在列车牵引负荷突然发生变化时,将所提出的IVACC方法与IVSM方法和在改进的VSM基础上的bang-bang控制进行性能对比,此案例在仿真过程中暂时不考虑接触线上接触电阻的损耗。
在仿真过程中,假设在t=3 s时列车负载从28 Ω突然降到14 Ω,系统发生暂态扰动。如图9a所示,电压和频率都在暂态扰动发生后一定时间内恢复系统稳定。从图中可以看出,基于所提出的IVACC策略,列车端电压下降幅度大约70 V左右,在电压允许范围之内,并且大约在3.8 s左右恢复稳定,相比较于其他两种方法,振荡幅度明显减少,控制效果更好一些。同理,如图9b~图9d所示,对于每个TSS系统的角频率变化来说,所提出的IVACC策略,相比较于其他两种方法,振荡幅度更少,超调量更小,响应速度明显更快,达到系统恢复稳定的时间更少,从而验证了所提控制策略的性能优越性。
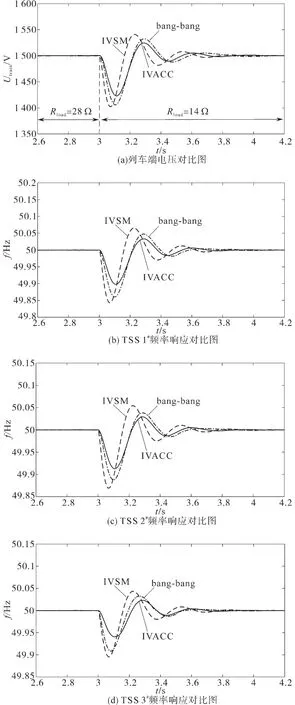
图9 基二三种策略的TSSs控制性能对比图Fig.9 The comparison diagram of control performance of TSSs based on three strategies
此外,为验证所提出的IVACC方法中基于一致性的自适应协同控制的性能,将自适应协同控制与无协同控制进行了对比分析。同样地,假设在t=3 s时发生暂态扰动,考虑以每个TSS系统频率与相邻TSS系统频率之间的同步误差作为验证依据,如图10所示。从图中可以看出,相比较于无协同控制,在基于协同控制下的每个TSS系统频率与相邻TSS系统频率的同步误差更小。同步误差越小,则说明系统频率之间越接近,达到频率响应变化的一致性越快,恢复稳定的时间将越短,从而验证了所提出的基于一致性的自适应协同控制的有效性。

图10 基二一致性的协同与无协同控制的同步误差对比Fig.10 Comparison of synchronization errors between consistencybased cooperation and non-cooperative control
5 结论与展望
5.1 结论
本文对城市轨道交通牵引供电系统控制问题进行了研究,提出了一种基于改进VSM的自适应协同控制策略,通过仿真分析得出结论如下:
1)本文提出的适用于牵引整流器的改进VSM控制作为一次控制能够有效地控制城市轨道交通的牵引系统,并保持直流母线电压的暂态稳定,使牵引网具有一定的惯性和阻尼支撑。
2)本文在基于改进VSM控制的牵引系统上,提出了一种自适应协同控制的方法作为二次控制来优化牵引系统,有效地减缓了系统的波动,使系统在发生暂态扰动时能够快速恢复稳定。
3)本文考虑了城市轨道交通TSSs的相对距离以及接触电阻损耗的问题,利用局部变电站感知相邻变电站之间的信息的作用进行多智能体协同控制,从而达到系统恢复稳定的一致性,通过仿真验证了所提控制策略的有效性。
5.2 展望
本文考虑到所研究的城轨交通牵引系统规模较大,进行实验验证有一定难度,所以在较为理想化的条件下进行了仿真模拟,验证了所提控制策略的有效性;这难免与实际牵引供电系统中会有一定的差异,未来的工作中将主要考虑以下差异性:
1)接触线电阻变化。在仿真条件中固定接触线的电阻,但在实际牵引供电系统中接触电阻在一段时间磨损后会发生变化,从而影响运行参数电压、频率的幅度,但是在本文控制方法下该变化情况都将是在可控范围之内。
2)牵引变电站之间的通讯时延。牵引供电系统中通讯网络在实际应用中会存在信息时延的情况,可能会影响多牵引变电站之间同步跟踪的精度,但不会影响最终的稳定趋势。

