基于DFFRLS和神经网络-ASRUKF算法的蓄电池SOC估计

顾钟凡，陈玉伟，李承澳，张德春，黄海

（河海大学能源与电气学院，江苏 南京 210098）

近年来，伴随着我国提出的电力物联网以及能源互联网战略，可再生能源技术得到了极大的发展，新能源汽车作为可再生能源技术的重大商业应用，已经逐步成为主流出行方式[1-2]。而蓄电池作为新能源汽车的动力来源，由于其工作状况极其复杂且不具有普遍性，需要建立合适的电池管理系统（battery management system，BMS）实时获取蓄电池的工作状态，其内部状态主要包括荷电状态（state of charge，SOC）和健康状态（state of health，SOH）[3-4]。其中，SOC为电池管理系统最核心的技术之一，精确的SOC估计可以使蓄电池得到充分的利用，对电池管理系统具有重大的意义[5-6]。

目前对SOC估计的方法有很多种，主要分为以下几类：安时积分法、开路电压法、神经网络法和基于等效模型法[7]。安时积分法作为一种开环的估计方法，其SOC的估计误差会随着时间进行累积，最终将无法满足SOC估计精度的要求，且其SOC估计结果受SOC初值的影响较大。开路电压法在估计SOC之前需要将蓄电池开路静置很长一段时间来保证SOC估计的准确性，因此不适用于在线估计[8]。神经网络法采用大数据训练来估计SOC，但其每次训练结果都不同且估算精度受训练方法的影响较大[9]。基于等效模型的SOC估计方法主要为拓展卡尔曼滤波法（extend Kalman filter，EKF）及其延伸无迹卡尔曼滤波法（unscented Kalman filter，UKF）。EKF在对系统进行线性化的过程中忽略了泰勒展开后的二次及以上高次项，使得系统存在线性化误差。UKF通过无迹变换来获取过程噪声协方差的统计量，但UKF需要人为指定噪声协方差初值，使得SOC估计存在噪声误差，同时UKF无法保证状态协方差矩阵的半正定性，影响程序运行[10-11]。

为了解决上述问题，本文选择3.5 V/20 A·h的磷酸铁锂电池为研究对象，首先建立二阶Thevenin等效RC电路模型，并建立状态方程和观测方程；然后采用BP神经网络代替多项式拟合OCV-SOC曲线，提高了曲线拟合精度；再建立以动态遗忘因子递推最小二乘（dynamic forgetting factor recursive least square，DFFRLS）法和自适应平方根无迹卡尔曼滤波（adaptive square-root unscented Kalman filter，ASRUKF）算法进行SOC联合估计：通过DFFRLS在线辨识模型参数，采用ASRUKF算法进行SOC估计；最后，设计物理实验，对比本算法与平方根无迹卡尔曼滤波（square-root unscented Kalman filter，SRUKF）及UKF、自适应无迹卡尔曼滤波（adaptive unscented Kalman filter，AUKF）算法进行分析SOC估计结果的精度和收敛性。

1 蓄电池建模及参数辨识

1.1 二阶Thevenin等效模型建立及离散化处理

蓄电池SOC的估计精度依赖于精确的电路模型，目前国内外普遍采用的模型有：Rint模型、一阶RC模型、PNGV模型和二阶Thevenin等效电路模型[12-13]，二阶Thevenin等效电路模型相比于一阶RC模型能够更加精确反映蓄电池的静动态特性，同时也便于进行蓄电池特性分析和参数辨识。因此本文选用二阶Thevenin等效电路模型进行蓄电池建模，其电路原理图如图1所示。

图1 亊阶Thevenin等效电路模型Fig.1 Second-order Thevenin equivalent circuit model

图1中，Uoc为电池的开路电压（opening circuit voltage，OCV），是关于SOC的函数；I为电池工作时的电流；R0为电池欧姆内阻；Rs，Rl，Cs，Cl，Us，Ul分别为电池的2个极化电阻、极化电容和极化电压；U为蓄电池工作时的端电压。

根据图 1 中的等效模型，选取SOC，Us，Ul作为系统状态变量，采用拉氏变换和脉冲响应不变法进行离散化[14]，令，可得状态空间离散化模型如下式：

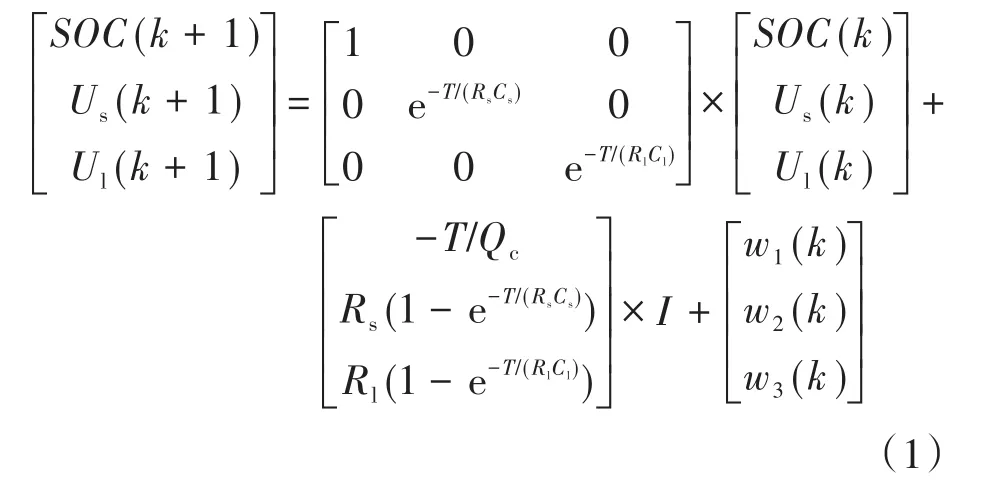
式中：k为离散后的时间；T为数据采样周期（本文中为1 s）；Qc为电池额定容量（本文中为20 A·h）；wk为系统噪声。

1.2 基于DFFRLS的电池模型在线参数辨识

1.2.1 OCV-SOC曲线输出方程拟合

如图1所示，为了获取以工作电流I作为输入，端电压U作为输出的输出方程，根据基尔霍夫定律可知，开路电压Uoc与端电压U之间存如下关系：

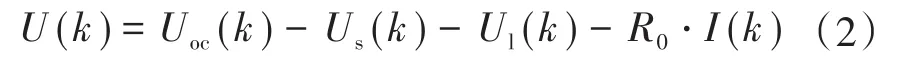
由于开路电压Uoc与蓄电池SOC之间存在着一一对应的映射关系，因此Uoc可以表示为SOC的函数，如下式所示：

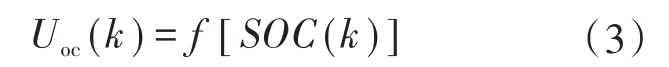
式中：f[·]为关于SOC（k）的非线性函数。

对于函数f[·]的求取，普遍采用多项式拟合的方法，但多项式拟合必然会因为选取多项式阶次不足或阶次过高而造成拟合精度不足或过拟合现象的出现[15-16]，因此，本文提出一种采用BP神经网络代替多项式进行OCV-SOC拟合的方法，BP神经网络拥有可逼近任意复杂程度非线性关系的特点，可通过充分的网络训练极大地提高拟合精度。

本文将六阶多项式与BP神经网络拟合效果进行对比，多项式拟合函数如下式所示：

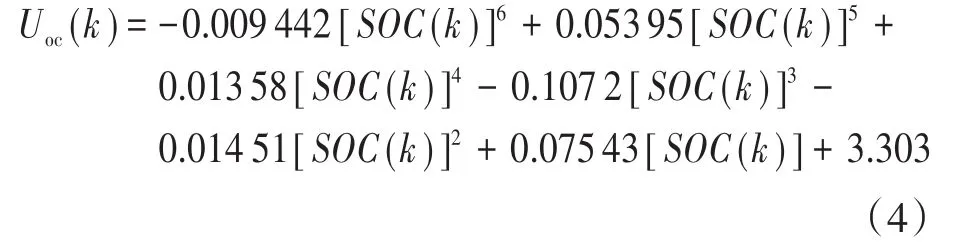
二者拟合效果对比如图2所示。

图2 两种拟合方法效果对比图Fig.2 Comparison of the effects of the two fitting methods

由图2可以看出，BP神经网络法的拟合效果与拟合精度均优于六阶多项式拟合，且BP神经网络的拟合优度R2=0.999 8，六阶多项式的拟合优度R2=0.961 4，进一步说明BP神经网络拟合精度更高。

1.2.2 DFFRLS在线参数辨识

目前对于蓄电池的在线参数辨识常用递推最小二乘（recursive least square，RLS）法，即每次根据新的实验数据，在前一次估计值的基础上，利用新数据对前估计值修正，从而递推得出新的估计值[17]。但RLS在递推迭代的过程中存在因旧数据不断积累而淹没新数据的缺陷，特别是在蓄电池系统中存在着大量的实验数据，导致参数辨识结果精度下降。文献[18]中提出了遗忘因子递推最小二乘（forgetting factor recursive least square，FFRLS）法，引入的遗忘因子一定程度上能够克服“数据饱和”的现象，起到“突出新数据”的特点，但固定遗忘因子的FFRLS在参数辨识过程中难以同时满足快速性和收敛性，因此本文基于FFRLS，提出了基于时变动态遗忘因子的DFFRLS，通过理论模型与实际模型输出量的差值为变量来构建遗忘因子调节函数，从而实现遗忘因子的动态调整。

2 蓄电池SOC估计方法

2.1 ASRUKF算法

目前对蓄电池SOC的估计多基于卡尔曼滤波算法及其拓展，由于采用UKF算法估计蓄电池SOC时需要人为指定噪声协方差初值，使得SOC估计存在噪声误差，同时UKF也无法保证状态协方差矩阵的半正定性，影响程序正常运行，文献[19]中提出一种基于Sage-Husa自适应滤波与UKF相结合的思想，设计AUKF滤波器进行SOC估计，该算法能够实时更新噪声协方差矩阵，降低了人为设定噪声协方差初值对估计精度的影响。考虑到AUKF仍无法保证状态协方差矩阵的半正定性，本文提出一种基于AUKF的改进算法，在自适应滤波算法的基础上结合平方根滤波算法，构成ASRUKF滤波器。平方根滤波算法中不直接采用噪声误差进行算法运算而用噪声误差的平方根进行算法的运算，能够有效保证状态协方差矩阵的半正定性[20]。

2.2 DFFRLS和BP-ASRUKF联合估计算法

本文在1.2和2.1部分详细论述了DFFRLS参数辨识和ASRUKF算法的实现步骤，DFFRLS和BP-ASRUKF进行SOC联合估计具体步骤如下：

1）根据 DFFRLS 算法在线辨识参数[R0（k）Rs（k）Cs（k）Rl（k）Cl（k）]；

2）根据辨识的参数完成ASRUKF算法的更新；

3）根据ASRUKF算法进行SOC估计；

4）将SOC估计值通过BP神经网络拟合的OCV-SOC曲线映射关系获取Uoc的值，引入到DFFRLS算法中完成Uoc（k）的更新。

整个算法过程实现了蓄电池模型参数在线辨识和蓄电池SOC估计的闭环修正，提高了SOC估计的收敛性和估计精度，具体算法的流程框图如图3所示。

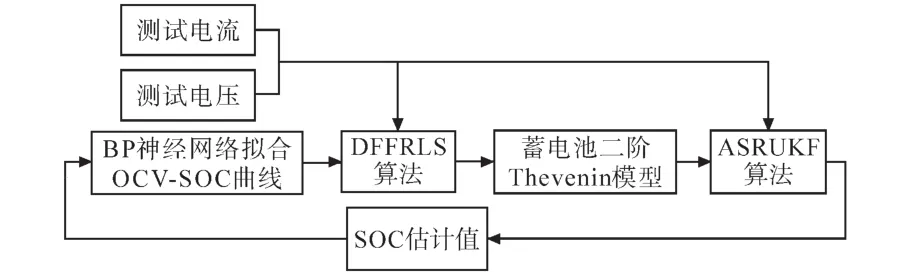
图3 DFFRLS和ASRUKF联合估计流程图Fig.3 Flow chart of DFFRLS and ASRUKF joint estimation

3 实验验证和仿真分析

为了验证本文所建立的DFFRLS和BP-ASRUKF联合估计SOC算法的收敛性和精确性，本文设计了基于型号为LAND电池测试系统CT2001D对磷酸铁锂电池进行循环动态压力测试（dynamic stress test，DST）工况实验，具体实验设备见图4所示，通过平台恒温恒湿箱控制温度为25℃，蓄电池初始SOC值为100%，在初始值已知且准确的情况下，本文采用安时积分法来计算各个时间点的SOC值作为真值与各种算法估计值进行比较分析，DST放电电流波形如图5所示。

图4 电池测试实验设备Fig.4 Battery test equipment

图5 DST工况放电电流波形图Fig.5 Waveform of discharge current at DST condition

3.1 BP-ASRUKF、其余算法估计SOC效果对比

为了验证本文提出的DFFRLS和BP-ASRUKF联合估计SOC算法的有效性和精确性，本文选用蓄电池模型同为二阶Thevenin模型，采用最小递推二乘法进行参数在线辨识的SRUKF，AUKF和UKF算法与本文提出的算法进行SOC估计效果对比，图6为设定相同SOC初值（SOC0=100%）下采用不同算法估计的SOC变化曲线与SOC真实曲线的对比，图7为不同算法估计下SOC随时间变化的误差ΔSOC曲线。

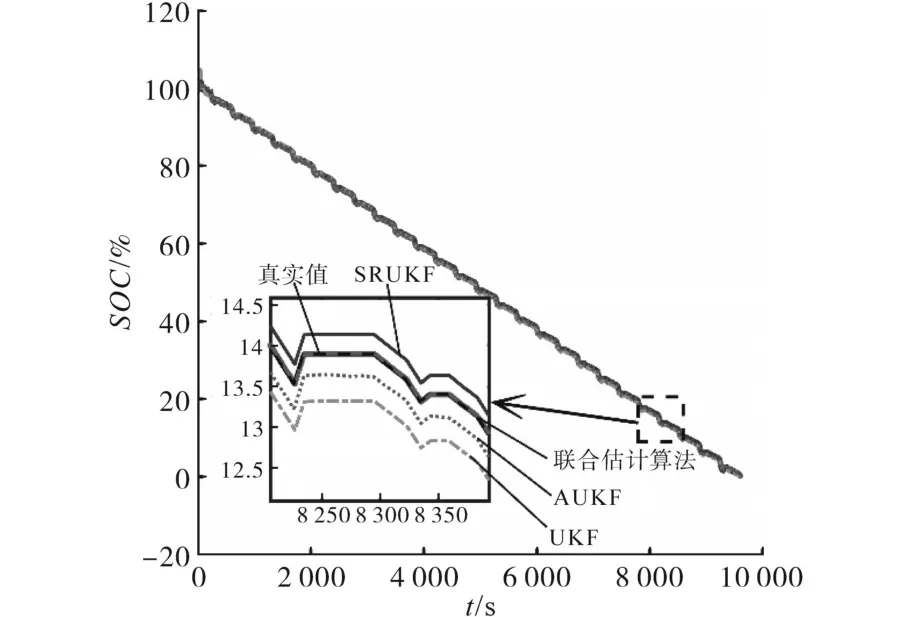
图6 SOC初值为100%时不同算法估计值Fig.6 Estimates of different algorithms when initial SOC is 100%

图7 SOC初值为100%时不同算法估计误差Fig.7 Estimation error of different algorithms when initial SOC is 100%

由图6可知，联合估计SOC算法与SRUKF，AUKF和UKF算法估计的蓄电池SOC变化的趋势基本一致且均能收敛到真实的SOC值，由放大图可以看出，本文提出的联合估计SOC算法更接近于真实的SOC值。

由图7可知，4种算法稳态误差均趋于零，本文提出的联合估计算法相比于其他算法更能够有效地降低累计误差、具有更高的精度。

表1为4种不同算法估计SOC的最大绝对误差、平均绝对误差和均方根误差的数据比较，进一步验证了本文所建立的算法具有更高的精确度。

表1 4种算法的误差数据比较Tab.1 Data error comparison among four methods

3.2 改变初值后不同算法SOC估计收敛性分析

为了比较本文提出的DFFRLS和BP-ASRUKF联合估计SOC算法与SRUKF，AUKF及UKF算法对SOC估计的收敛性，本文通过改变SOC的初值（SOC0=80%）来探究不同算法下的SOC估计值向真实值的收敛速度，根据不同算法下SOC估计值收敛到真实值所需的时间来评判算法的收敛性。

改变SOC初值为80%时，上述4种不同算法对SOC估计的收敛曲线如图8所示，上述4种不同算法对SOC估计的误差曲线如图9所示。

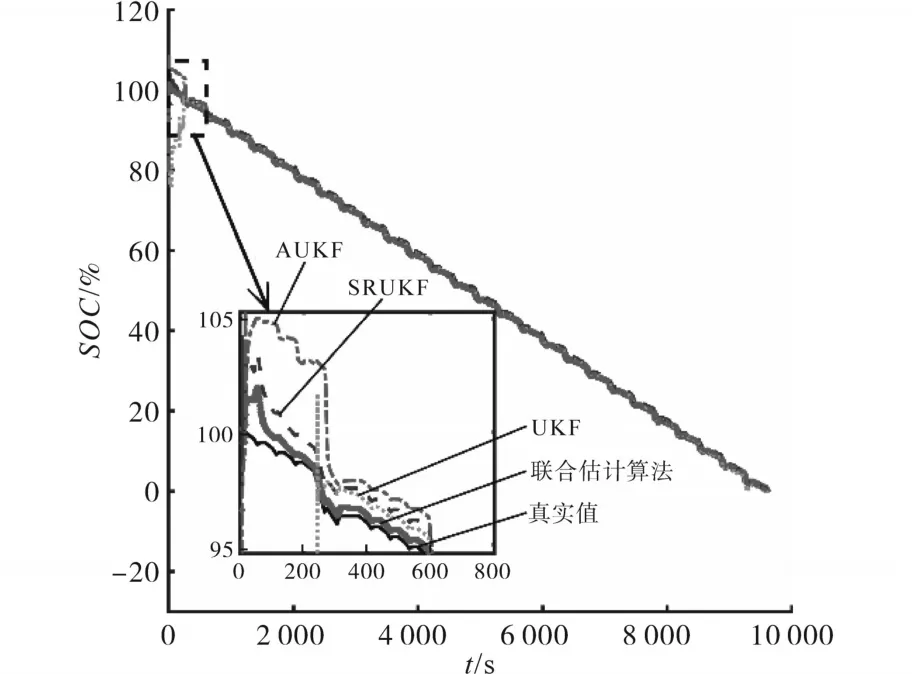
图8 SOC初值为80%时不同算法收敛曲线Fig.8 Convergence curves of different algorithms（SOC0=80%）

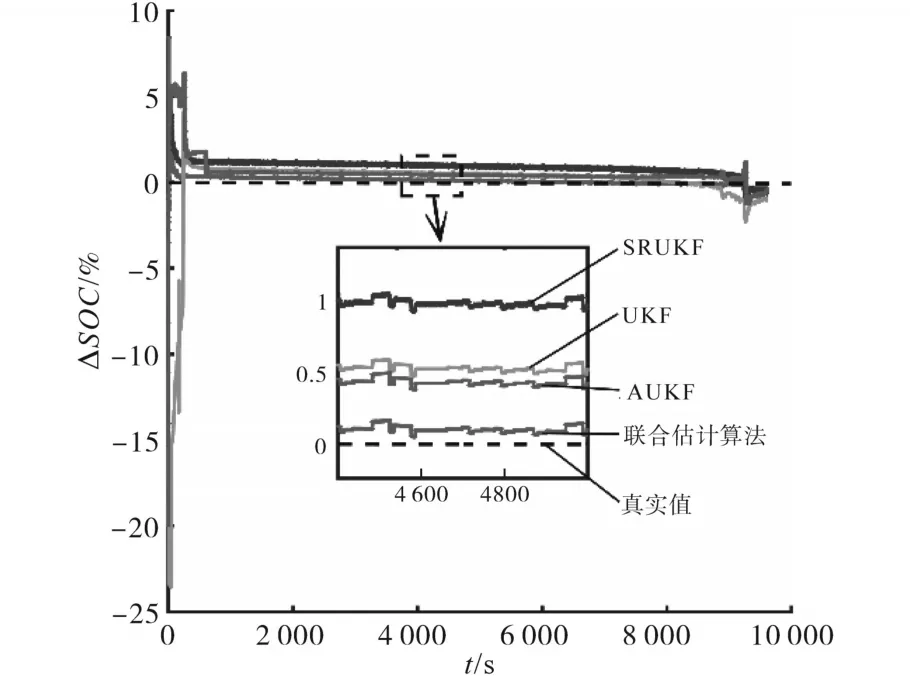
图9 SOC初值为80%时不同算法估计误差Fig.9 Estimation error of different algorithms（SOC0=80%）

由图8可知，SRUKF，AUKF及UKF算法均需要300个时间断面才能使SOC估计值收敛到真实值，而本文所建立的DFFRLS和BP-ASRUKF联合估计算法只需要100个时间断面便可收敛到真实值，且在SOC收敛过程中超调量最小，由此说明本文建立的DFFRLS和BP-ASRUKF联合估计算法相比于传统算法具有更好的收敛性。

由图9可明显看出DFFRLS和BP-ASRUKF联合估计算法在任意时刻的SOC估计误差均小于其余三种传统算法，再次说明本文建立的算法对SOC估计效果更佳且精确度更高。

4 结论

本文选择3.5 V/20 A·h的磷酸铁锂电池为研究对象，建立二阶Thevenin等效RC电路模型，分析神经网络、DFFRLS和ASRUKF算法的特点，建立了DFFRLS和BP-ASRUKF联合估计算法，实现对DST工况下磷酸铁锂电池的SOC在线估计，并与其余三种方法进行比较，得出以下结论：

1）在DST工况条件下，采用BP神经网络代替多项式拟合OCV-SOC曲线可以进一步提高曲线拟合精度，从而提高参数在线辨识的精度。

2）在参数在线辨识中，DFFRLS算法采用动态变化的遗忘因子，能够进一步降低“数据饱和”现象，相较于FFRLS及RLS算法具有更好的快速性和精确性。

3）在SOC估计中，引入Sage-Husa自适应滤波和平方根滤波算法，使噪声协方差矩阵实时更新的同时保证状态协方差矩阵的半正定性，降低了噪声协方差初值设定对估计精度的影响。

4）本文建立的DFFRLS和BP-ASRUKF联合估计算法相比于其他三种算法具有更好的收敛性、快速性和精确性。

本文重点描述了DFFRLS和ASRUKF联合算法进行SOC在线估计的问题，实验环境温度保持为25℃，接下来可探究不同温度对SOC在线估计的影响。